Acoperiri convexe in plan Universitatea Politehnica Bucuresti Catedra

Acoperiri convexe in plan Universitatea “Politehnica” Bucuresti Catedra de Calculatoare conf. dr. ing. Costin-Anton BOIANGIU costin. boiangiu@cs. pub. ro

Convexitate • O multime S este convexa daca pentru orice pereche de puncte p, q S avem segmentul pq S. p p q convexa q nonconvexa • Formal, daca S este o multime intr-un spatiu vectorial real sau complex:

Infasuratori convexe (Convex Hull) Fie o multime S = {p 1, p 2, …, p. N}. Infasuratoarea convexa CH(S) este: • Cel mai mic poligon convex care contine toate punctele din S • Intersectia tuturor multimilor convexe ce contin S • Intersectia tuturor semispatiilor ce contin S • Reuniunea tuturor triunghiurilor determinate de puncte in S • Multimea tuturor combinatiile convexe de puncte din S

Aplicatii • Detectia coliziunilor ▫ jocuri video: inlocuitor mai bun pentru bounding-box • Aproximarea si compararea formelor ▫ pattern matching • Pas de preprocesare pentru multi algoritmi in geometria computationala • Diametrului unui set de puncte este distanta maxima dintre doua puncte din CH • Infasuratoarea convexa este cea mai raspandita structura in geometria computationala

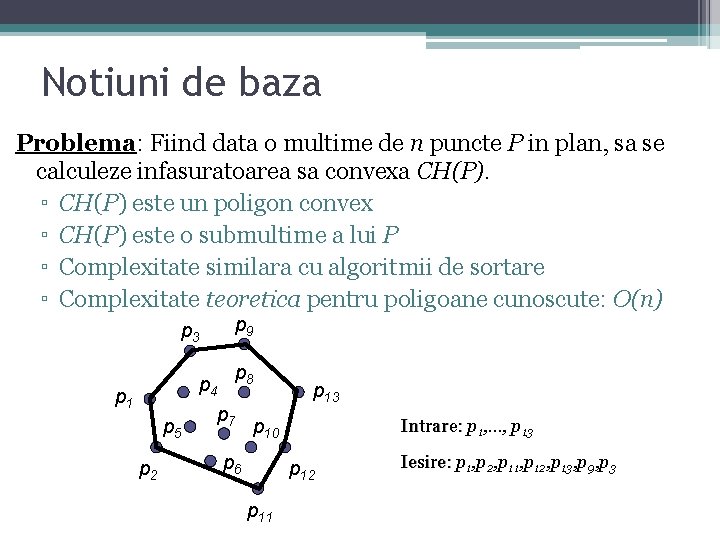
Notiuni de baza Problema: Fiind data o multime de n puncte P in plan, sa se calculeze infasuratoarea sa convexa CH(P). ▫ CH(P) este un poligon convex ▫ CH(P) este o submultime a lui P ▫ Complexitate similara cu algoritmii de sortare ▫ Complexitate teoretica pentru poligoane cunoscute: O(n) p 3 p 1 p 5 p 2 p 9 p p 4 8 p 7 p 10 p 6 p 13 Intrare: p : 1, …, p 13 p 12 p 11 Iesire: p : 1, p 2, p 11, p 12, p 13, p 9, p 3

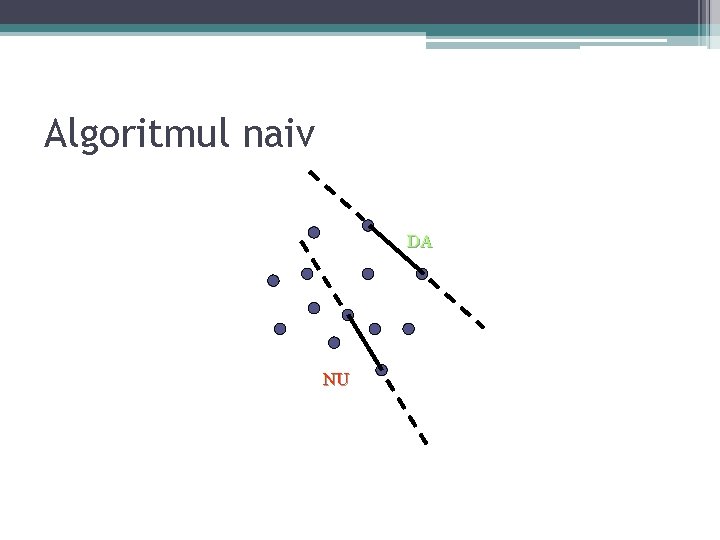
Algoritmul naiv DA NU

Algoritmul naiv Algoritm • Pentru fiecare pereche de puncte se construiesc segmentul dintre ele si dreapta suport • Se gasesc toate segmentele ale caror drepte suport impart planul in doua jumatati, astfel incat un semiplan contine toate celelalte puncte. • Se construieste infasuratoarea convexa din aceste segmente. Complexitate ▫ Toate perechile: ▫ Se verifica toate punctele pentru fiecare pereche: O(n) fiecare, O(n 3) in total.

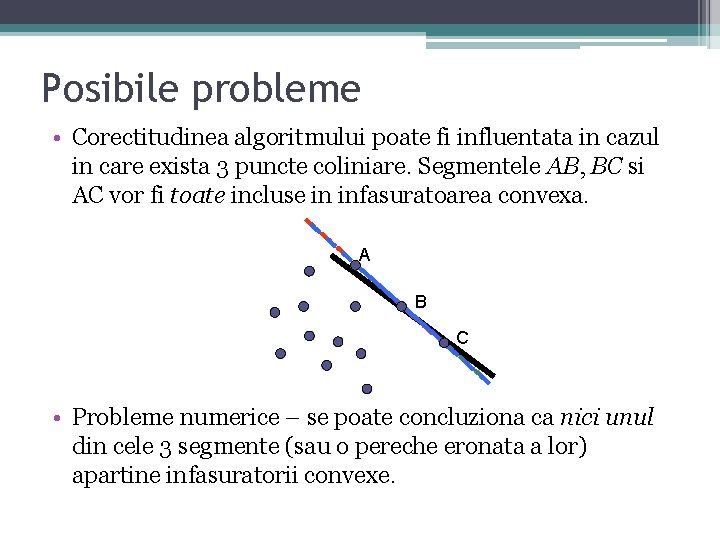
Posibile probleme • Corectitudinea algoritmului poate fi influentata in cazul in care exista 3 puncte coliniare. Segmentele AB, BC si AC vor fi toate incluse in infasuratoarea convexa. A B C • Probleme numerice – se poate concluziona ca nici unul din cele 3 segmente (sau o pereche eronata a lor) apartine infasuratorii convexe.

Presupuneri legate de pozitia punctelor • Cand se modeleaza un algoritm geometric, mai intai facem unele presupuneri cu scop de simplificare, ex: ▫ Nu exista 3 puncte coliniare ▫ Nu exista 2 puncte cu aceeasi coordonata x sau y ▫ Altele: nu exista 3 puncte pe acelasi cerc, etc. • Mai tarziu se ia in considerare cazul general: ▫ ▫ Comportamentul algoritmului la cazuri speciale Va ramane algoritmul corect? Va ramane timpul de rulare neschimbat? Se va modifica/extinde algoritmul pentru a trata aceste situatii.

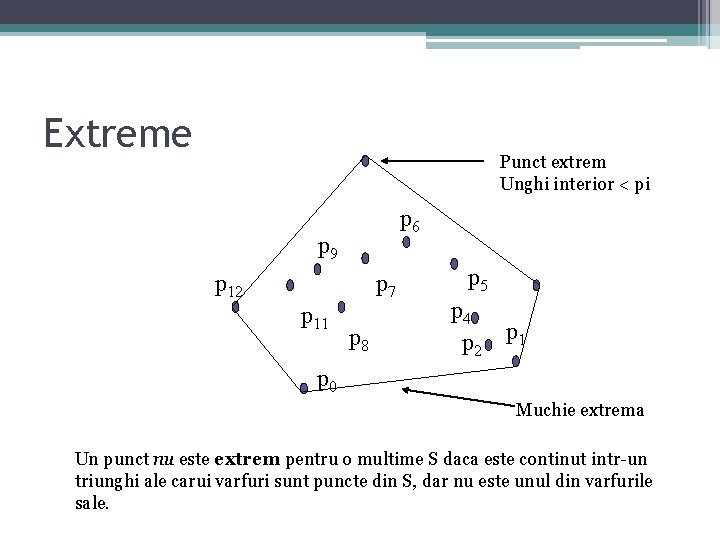
Extreme Punct extrem Unghi interior < pi p 6 p 9 p 12 p 7 p 11 p 8 p 5 p 4 p 2 p 1 p 0 Muchie extrema Un punct nu este extrem pentru o multime S daca este continut intr-un triunghi ale carui varfuri sunt puncte din S, dar nu este unul din varfurile sale.

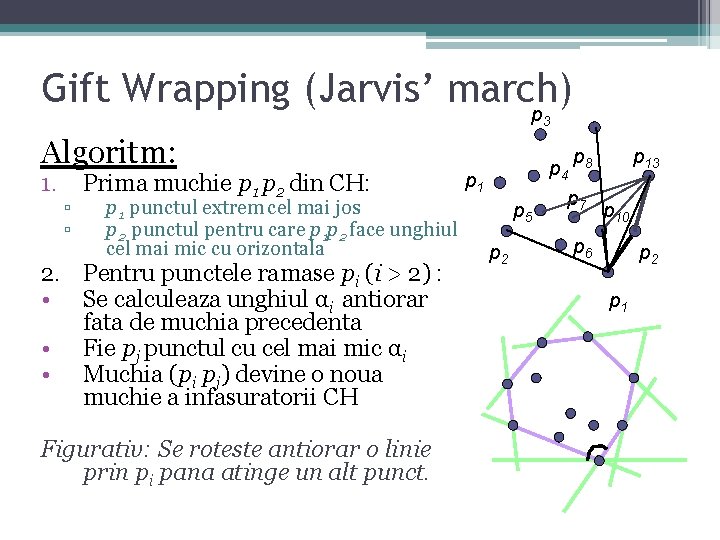
Gift Wrapping (Jarvis’ march) p 3 Algoritm: 1. ▫ ▫ Prima muchie p 1 p 2 din CH: p 1 punctul extrem cel mai jos p 2 punctul pentru care p 1 p 2 face unghiul cel mai mic cu orizontala 2. Pentru punctele ramase pi (i > 2) : • Se calculeaza unghiul αi antiorar fata de muchia precedenta • Fie pj punctul cu cel mai mic αi • Muchia (pi pj) devine o noua muchie a infasuratorii CH Figurativ: Se roteste antiorar o linie prin pi pana atinge un alt punct. p 1 p 5 p 2 p p 4 8 p 7 p 13 p 10 p 6 p 2 p 1

12 Equatia dreptei • (x 1, y 1) si (x 2, y 2) doua puncte. • Ecuatia explicita a dreptei: (x 2, y 2) y = mx+c (x 1, y 1) m = tan θ c • Caz particular: x 1= x 2 (dreapta verticala)

Complexitate • n puncte, la fiecare pas n comparatii: O(n 2) • De fapt complexitatea este O(nh) , h = |CH(S)| • De obicei h << n si atunci este comparabil cu algoritmul lui Graham O(n logn)

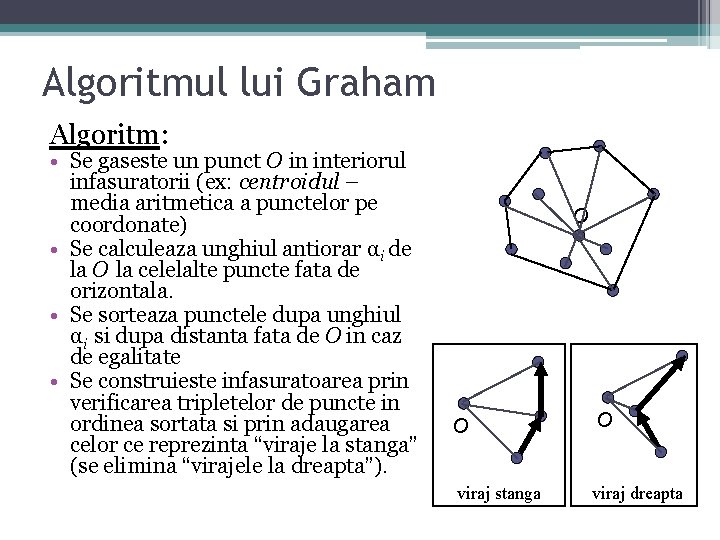
Algoritmul lui Graham Algoritm: • Se gaseste un punct O in interiorul infasuratorii (ex: centroidul – media aritmetica a punctelor pe coordonate) • Se calculeaza unghiul antiorar αi de la O la celelalte puncte fata de orizontala. • Se sorteaza punctele dupa unghiul αi si dupa distanta fata de O in caz de egalitate • Se construieste infasuratoarea prin verificarea tripletelor de puncte in ordinea sortata si prin adaugarea celor ce reprezinta “viraje la stanga” (se elimina “virajele la dreapta”). O O O viraj stanga viraj dreapta

Exemplu • Daca p 1 p 2 p 3 vireaza dreapta sau sunt coliniare, se elimina p 2 din CH(S) si se continua cu p 0 p 1 p 3 • Daca p 1 p 2 p 3 vireaza stanga, avanseaza la p 2 p 3 p 4 p 2 p 1 p 4 p 0 O

Parcurgerea punctelor din CH(S) 1. begin 2. v = START 3. w = PRED[v] /* w salveaza punctul dinainte de START */ 4. f = FALSE /* f indica daca scanarea a ajuns din nou la START */ 5. while (NEXT[v] START or f = FALSE) 6. if (NEXT[v] = w) then 7. f = TRUE 8. endif 9. if (Left(v, NEXT[v], NEXT[v]])) then 10. v = NEXT[v] /* avanseaza */ 11. else 12. delete NEXT[v] /* eliminare, operatie cu liste in O(1) */ 13. v = PRED[v] /* backtrack */ 14. endif 15. endwhile 16. end

Graham: analiza complexitatii • Se foloseste o stiva pentru procesarea punctelor sortate. • Complexitate: O(n log n) determinata de pasul de sortare • Di = numarul de puncte scoase din stiva la procesarea pi, • Fiecare punct este adaugat la stiva o singura data. • Odata ce un punct este scos din stiva nu poate fi adugat inca o data. • Asadar

Algoritmul Quick Hull (1) Partitia initiala • S este partitionata de o dreapta L determinata de punctele l, r S cu cea mai mica si cea mai mare abscisa (garantat distincte) • S(1) S este submultimea lui S deasupra L. • S(2) S este submultimea lui S sub L. • {S(1), S(2)} nu este o partitie stricta a lui S, S(1) S(2) {l, r}. • Urmeaza sa se construiasca CH(S(1)) si CH(S(2)), si apoi concatenate in CH(S). • Procesul este identic pentru S(1) si S(2), vom detalia numai S(1) r l L S(2)

Algoritmul Quick Hull (2) Alegerea extremului • Se cauta punctul h S(1) astfel incat 1. 2. triunghiul hlr are cea mai mare arie posibila daca h nu este unic determinat, se alege cel pentru care unghiul hlr este maxim. • Aceste conditii implica h H(S). De ce? • Se construieste prin h linia L paralela cu L • Conditia (1) impune ca nu vor exista puncte din S(1) (sau S) deasupra L , • Pot fi mai multe puncte pe L , dar h va fi cel mai din stanga, conform (2) h H(S). • h poate fi gasit in O(N) verificand fiecare punct din S(1). h S(1) L r l L

Algoritmul Quick Hull (3) Partitionarea • Se construiesc doua linii orientate, L 1 S(1, 1) dinspre l catre h, si L 2 dinspre h catre r. • Fiecare punct din S(1) se poate clasifica relativ la L 1 si L 2 • Nici un punct din S(1) nu poate fi situat in acelasi timp la stanga L 1 si L 2. l • Punctele la dreapta L 1 si L 2 nu apartin CH(S) fiind in interiorul triunghiului L L 1 hlr si sunt eliminate • Punctele la stanga L 1 formeaza S(1, 1). • Punctele la stanga L 2 formeaza S(1, 2) h r L 2 eliminate

Algoritmul Quick Hull (4) S(1, 2) Pasul recursiv • Procesul se reia pentru S(1, 1) si S(1, 2). h L 1 S(1, 2, 2) r l L • Recurenta continua pana cand S(…) are 0 puncte (toate punctele interne au fost eliminate), adica lr este o muchie din CH(S). L 2

Complexitate • Gasirea extremelor initiale se face in timp O(n). • La fiecare impartire, este nevoie de maxim n pasi pentru a determina h, dar timpul total al apelului recursiv depinde de marimile multimilor S(1) si S(2). Cazul favorabil Partitia este balansata • T(n) = 2 T(n/2) + O(n) T(n)=O(n log n). • O(n log n) se intampla pentru puncte distribuite aleator. Cazul defavorabil Partitie disproportionata • T(n) = T(n - 1) + O(n) = T(n - 1) + cn T(n) = O(n 2).

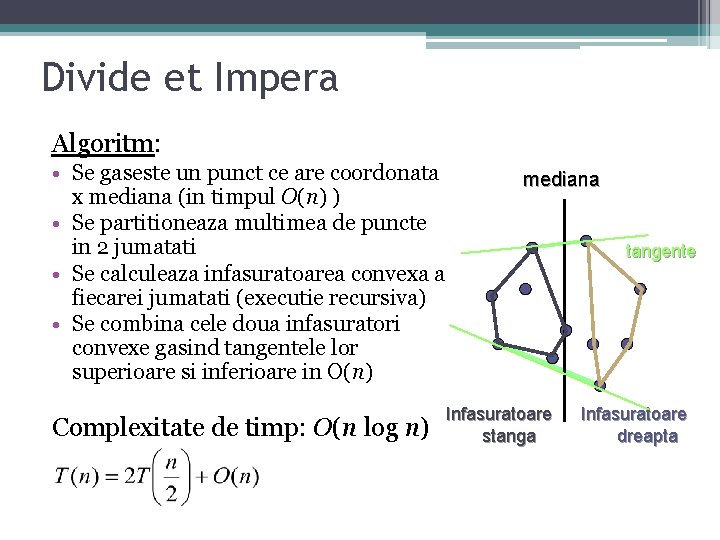
Divide et Impera Algoritm: • Se gaseste un punct ce are coordonata x mediana (in timpul O(n) ) • Se partitioneaza multimea de puncte in 2 jumatati • Se calculeaza infasuratoarea convexa a fiecarei jumatati (executie recursiva) • Se combina cele doua infasuratori convexe gasind tangentele lor superioare si inferioare in O(n) Complexitate de timp: O(n log n) mediana Infasuratoare stanga tangente Infasuratoare dreapta

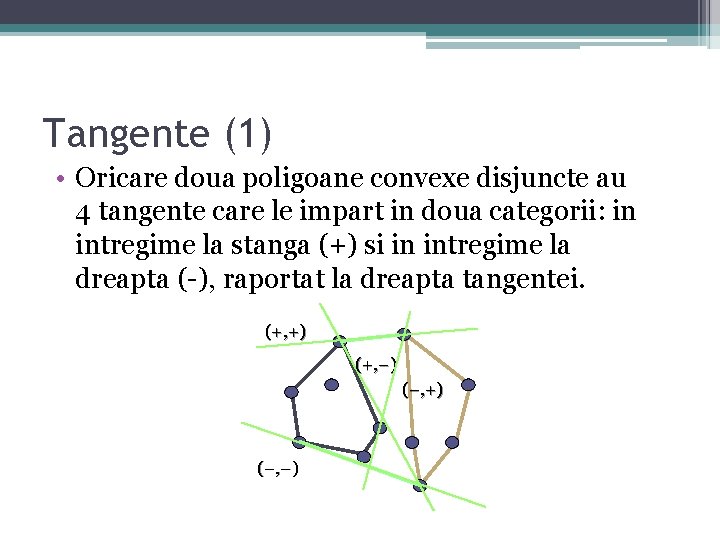
Tangente (1) • Oricare doua poligoane convexe disjuncte au 4 tangente care le impart in doua categorii: in intregime la stanga (+) si in intregime la dreapta (-), raportat la dreapta tangentei. (+, +) (+, −) (−, +) (−, −)

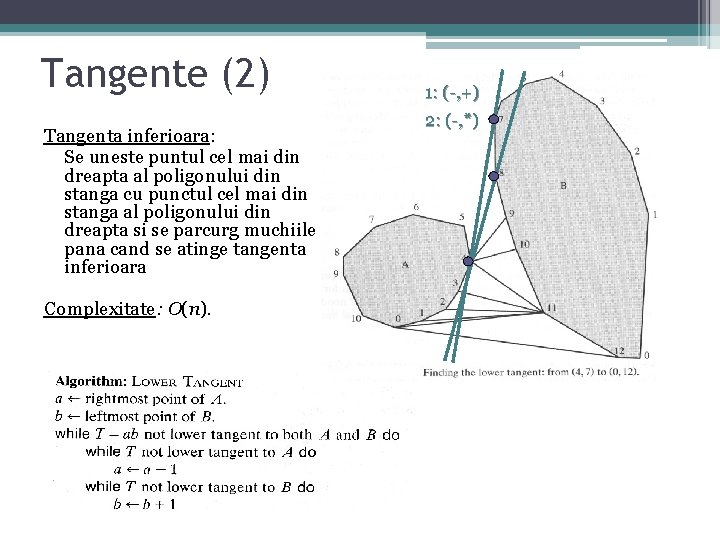
Tangente (2) Tangenta inferioara: Se uneste puntul cel mai din dreapta al poligonului din stanga cu punctul cel mai din stanga al poligonului din dreapta si se parcurg muchiile pana cand se atinge tangenta inferioara Complexitate: O(n). 1: (-, +) 2: (-, *)

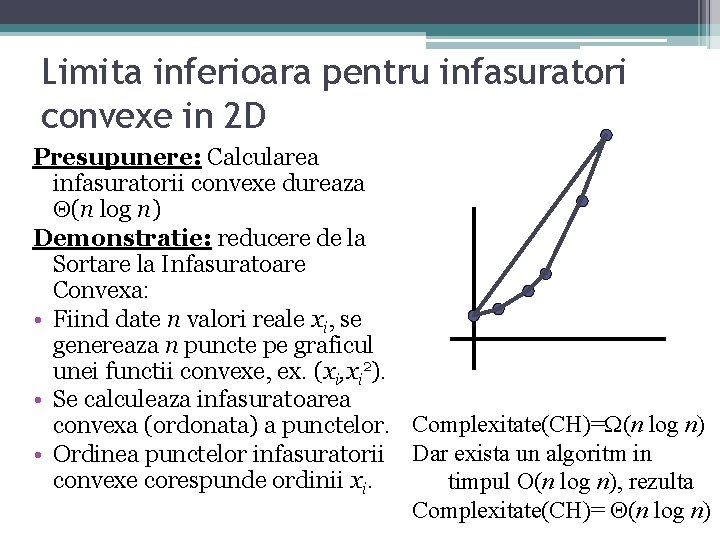
Limita inferioara pentru infasuratori convexe in 2 D Presupunere: Calcularea infasuratorii convexe dureaza (n log n) Demonstratie: reducere de la Sortare la Infasuratoare Convexa: • Fiind date n valori reale xi, se genereaza n puncte pe graficul unei functii convexe, ex. (xi, xi 2). • Se calculeaza infasuratoarea convexa (ordonata) a punctelor. Complexitate(CH)= (n log n) • Ordinea punctelor infasuratorii Dar exista un algoritm in convexe corespunde ordinii xi. timpul O(n log n), rezulta Complexitate(CH)= (n log n)

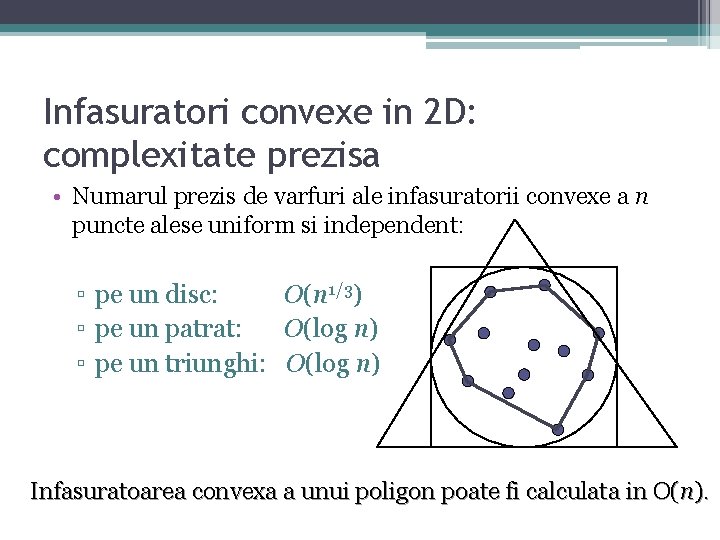
Infasuratori convexe in 2 D: complexitate prezisa • Numarul prezis de varfuri ale infasuratorii convexe a n puncte alese uniform si independent: ▫ pe un disc: O(n 1/3) ▫ pe un patrat: O(log n) ▫ pe un triunghi: O(log n) Infasuratoarea convexa a unui poligon poate fi calculata in O(n).

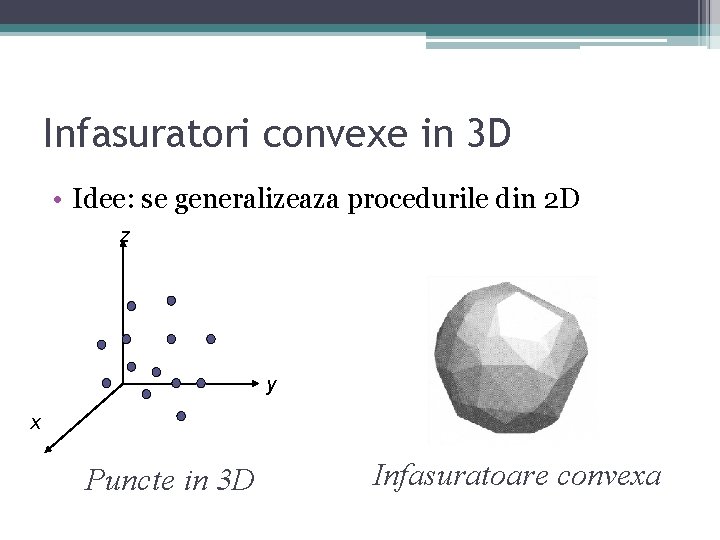
Infasuratori convexe in 3 D • Idee: se generalizeaza procedurile din 2 D z y x Puncte in 3 D Infasuratoare convexa

Infasuratori convexe in dimensiuni superioare Problema: fiind date n puncte in Rd, sa se gaseasca infasuratoarea lor convexa (numita si politop convex). • Fetele devin hiperfete de dimensiunea 2, 3, …, d– 1. • Hiperfetele formeaza o structura de graf unde adiacentele intre diferite entitati de dimensiunea i si i-1 sunt stocate. • Cativa din algoritmii prezentati mai devreme sunt aplicabili in dimensiuni superioare (in principiu), cu anumite extensii. Teorema 1: Infasuratoarea convexa de n puncte in spatiul d-dimensional are cel mult hiperfete. Teorema 2: infasuratoarea convexa poate fi calculata folosind algorimul “Gift Wrapping” in