Ackermann Steering Most vehicle steering systems use some

Ackermann Steering • Most vehicle steering systems use some form of the Ackermann Steering model. • For turning stability tires will turn on different radii.

Ackermann Steering

Ackermann Steering

Research • First step was to research steering geometries and types of mechanism suitable for our requirements. – Cheap – Rugged – Easily maintained – Readily available parts

Mechanism Selection • Mechanism should provide moderate responsiveness and ease of operation – Best choice – Recirculating Ball Steering Mechanism

Mechanism Elimination • Hydraulic – Failed Ease of Maintenance and availability of parts. • Rack and Pinion – Failed ease of operation at low speeds

Rough Geometry • Due to the suspension design I was required to follow the following setup.

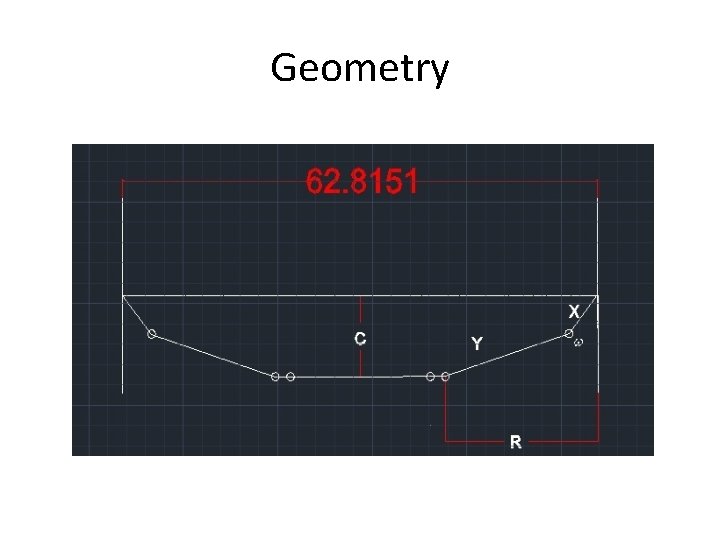
Geometry

Geometry

Geometry

Equations •

Left Side Equations •

Right Side Equations •

Equations Variable Description a Distance from knuckle to center link b Travel of center link c Distance from center link to axis of rotation x Length of steering knuckle y Tie rod length Angles between steering knuckle and tire Angle between knuckle and axis of rotation on the left side Angle between knuckle and axis of rotation on the right side Left turn angle Right turn angle

Program • • • • • • • #include <stdio. h> #include <math. h> #include <conio. h> int main(){ float y, c, b; double x= 6. 403; double P, Q, R, Theta 1, Gamma 1; double I, J, K, Theta 2, Gamma 2; printf("Input value for y: "); scanf("%f", &y); printf("Input value for c: "); scanf("%f", &c); printf("Input value for b: "); scanf("%f", &b); printf("The values entered are: %f, %fn", y, c, b); float a = 20. 1797; float g = 20. 1797; float pi = 3. 141592654; printf("a equals: %fn", a); printf("g equals: %fn", a); R = pow(y, 2) - pow(x, 2) - pow(b, 2) - pow(a, 2) - pow(c, 2) - 2*a*b; Q = 2*x*c; P = 2*x*(a+b); K = pow(y, 2) - pow(x, 2) - pow(b, 2) - pow(g, 2) - pow(c, 2) + 2*g*b; J = 2*x*c; I = 2*x*(g-b);

Program • • • • • • I = 2*x*(g-b); printf("P equals: %fn", P); printf("Q equals: %fn", Q); printf("R equals: %fn", R); printf("I equals: %fn", I); printf("J equals: %fn", J); printf("K equals: %fn", K); double den 1, den 2; double den 3, den 4; den 1 = sqrt( pow(P, 2) + pow(Q, 2) ); //denominator den 2 = den 1; //both denominators are the same den 3 = sqrt( pow(I, 2) + pow(J, 2) ); //denominator den 4 = den 3; //both denominators are the same Theta 1 = ((1 / cos((R/den 1)*(-1)) - 1 / cos(P/den 2))*(180/pi)); Theta 2 = ((1 / cos((K/den 3)*(-1)) - 1 / cos(I/den 4))*(180/pi)); printf("Theta 1 equals: %fn", Theta 1); printf("Theta 2 equals: %fn", Theta 2); Gamma 1 = (90 - 38. 66 - Theta 1); Gamma 2 = ( -90 + 38. 66 + Theta 2); printf("Gamma 1 equals: %fn", Gamma 1); printf("Gamma 2 equals: %fn", Gamma 2); getch (); return 0; }

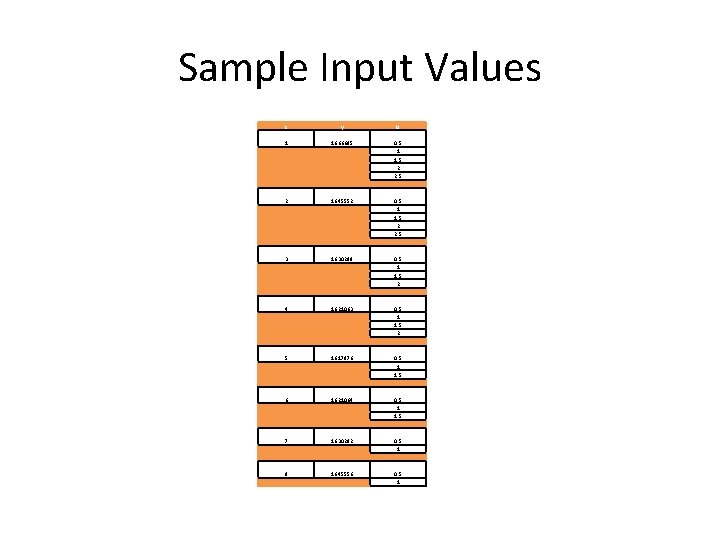
Sample Input Values c y b 1 16. 66685 0. 5 1 1. 5 2 2. 5 2 16. 45552 0. 5 1 1. 5 2 2. 5 3 16. 30289 0. 5 1 1. 5 2 4 16. 21063 0. 5 1 1. 5 2 5 16. 17976 0. 5 1 1. 5 6 16. 21064 0. 5 1 1. 5 7 16. 30292 0. 5 1 8 16. 45556 0. 5 1

Final Geometry •

Final Geometry � Turn Radii ◦ 7. 15 ft. (Inside) ◦ 11. 87 ft. (Outside

Parts

Constructed System

Deliverables �Mechanism Selection �Rough Geometry Selection �Geometric Equation Research �C++ Program �Calculations of Ackerman Angles �Final Geometry �Construction

Conclusion � Questions?