ACCUMULATION AP Calculus AB Days 7 8 Exploration

ACCUMULATION AP Calculus AB Days 7 -8

Exploration Accumulation from a Table

1. On a ship at sea, it is easier to measure how fast you are gong than it is to measure how far you have gone. Suppose you are a navigator aboard a supertanker. At 7: 30 you are 110 miles from the port you left from. The speed of the ship is measured each 15 minutes and recorded in the table below.
a. Make a plot of the data on the grid below. Be sure to think about units.
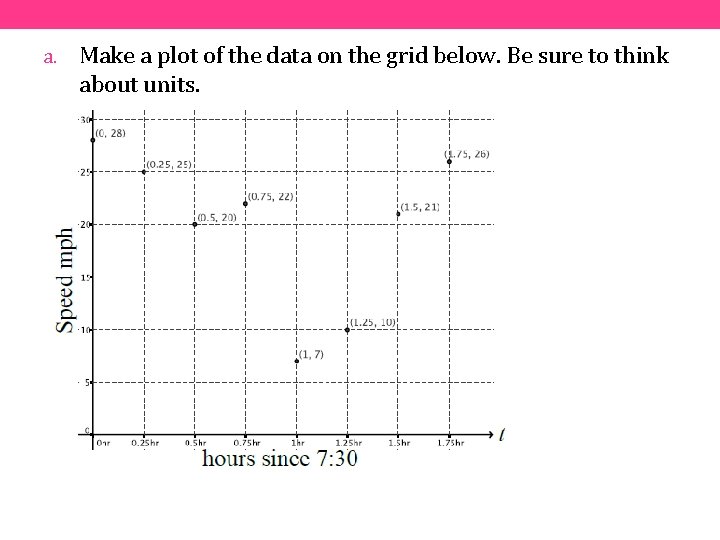
a. Make a plot of the data on the grid below. Be sure to think about units.

b. Estimate the distance the ship is from port (the ships position) every 15 minutes from 7: 30 p. m. and 9: 15 p. m. Explain your answer.

b. Estimate the distance the ship is from port (the ships position) every 15 minutes from 7: 30 p. m. and 9: 15 p. m. Explain your answer. Time t hours x(t) miles v(t) mph
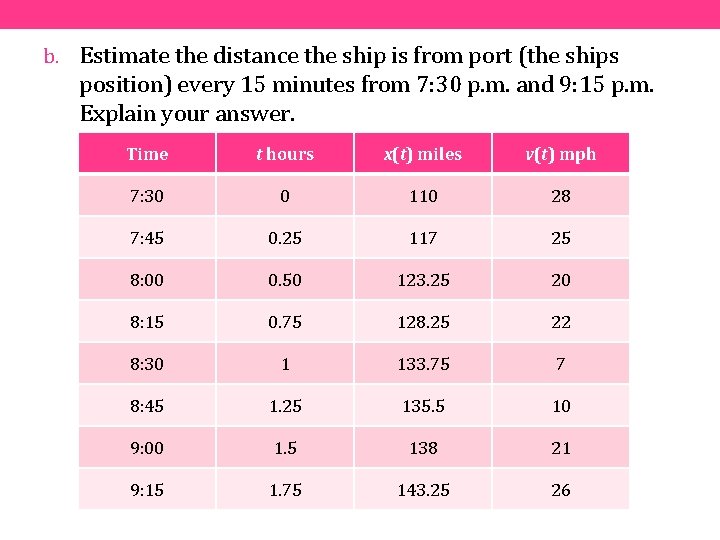
b. Estimate the distance the ship is from port (the ships position) every 15 minutes from 7: 30 p. m. and 9: 15 p. m. Explain your answer. Time t hours x(t) miles v(t) mph 7: 30 0 110 28 7: 45 0. 25 117 25 8: 00 0. 50 123. 25 20 8: 15 0. 75 128. 25 22 8: 30 1 133. 75 7 8: 45 1. 25 135. 5 10 9: 00 1. 5 138 21 9: 15 1. 75 143. 25 26

Discussion Do you think the ships speed went from 28 mph to 25 mph in an instance of time? Let’s revisit the graph, if the speed changes continuously, how could we approximate the positions x(t) more accurately.
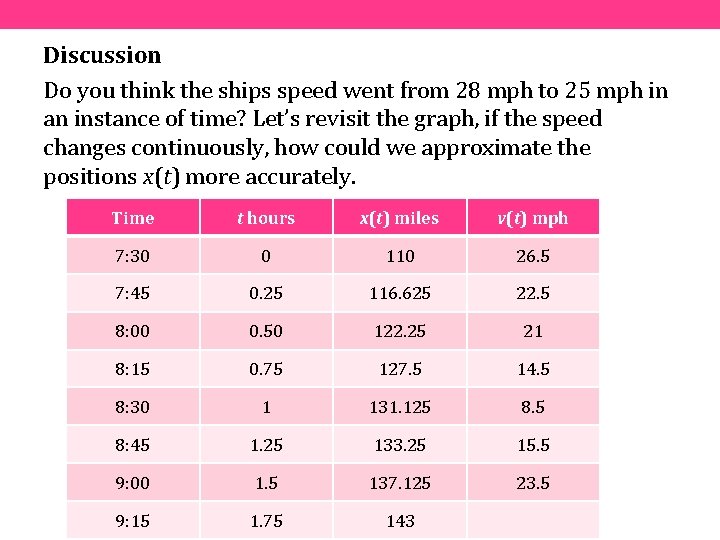
Discussion Do you think the ships speed went from 28 mph to 25 mph in an instance of time? Let’s revisit the graph, if the speed changes continuously, how could we approximate the positions x(t) more accurately. Time t hours x(t) miles v(t) mph 7: 30 0 110 26. 5 7: 45 0. 25 116. 625 22. 5 8: 00 0. 50 122. 25 21 8: 15 0. 75 127. 5 14. 5 8: 30 1 131. 125 8. 5 8: 45 1. 25 133. 25 15. 5 9: 00 1. 5 137. 125 23. 5 9: 15 1. 75 143

Discussion Why are these values lower than the rectangular sum done previously?


2. The velocity of a car, in ft/sec, traveling on a straight road, for 0 ≤ t ≤ 50 seconds, is given above in a table of values for v(t). Estimate with a trapezoidal sum the distance the car traveled in 50 seconds using the intervals indicated by the table. Show you arrived at your answer.

3. In 1993, Kara Hultgreen became one of the first female pilots authorized to fly navy planes in combat. Assume that as she comes in for a landing on the carrier, her speed in feet per second takes on the values shown in the table. Find, approximately, how far her plane travels as it comes to a stop. Is her plane in danger of running off the other end of the 800 -ft-long flight deck? Justify your answer.

Exploration 1 -3 a: Introduction to Definite Integrals
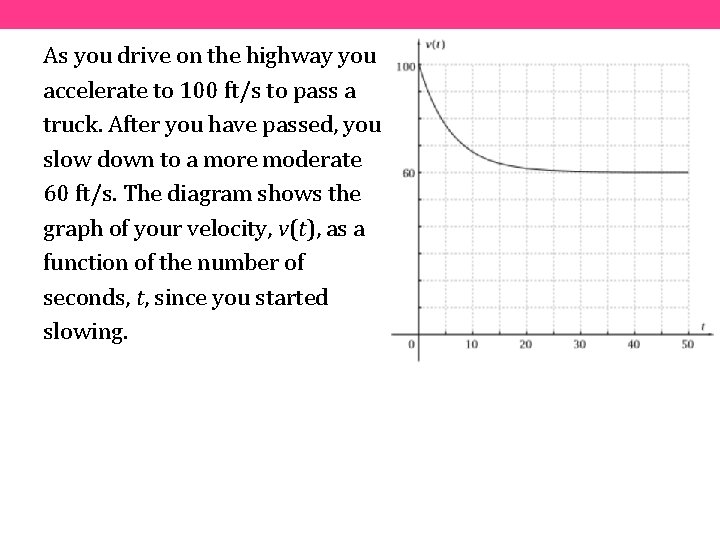
As you drive on the highway you accelerate to 100 ft/s to pass a truck. After you have passed, you slow down to a more moderate 60 ft/s. The diagram shows the graph of your velocity, v(t), as a function of the number of seconds, t, since you started slowing.

1. What does your velocity seem to be between t = 30 and t = 50 s? How far do you travel in the time interval [30, 50]? 2. Explain why the answer to Problem 1 can be represented as the area of a rectangular region of the graph. Shade this region.

3. The distance you travel between t = 0 and t = 20 can also be represented as the area of a region bounded by the (curved) graph. Count the number of squares in this region. Estimate the area of parts of squares to the nearest 0. 1 square space. For instance, how would you count this partial square?

4. How many feet does each small square on the graph represent? How far, therefore, did you go in the time interval [0, 20]?

5. Problems 3 and 4 involve finding the product of the x- value and the y-value for a function where y may vary with x. Such a product is called the definite integral of y with respect to x. Based on the units of t and v(t), explain why the definite integral of v(t) with respect to t in Problem 4 has feet for its units.
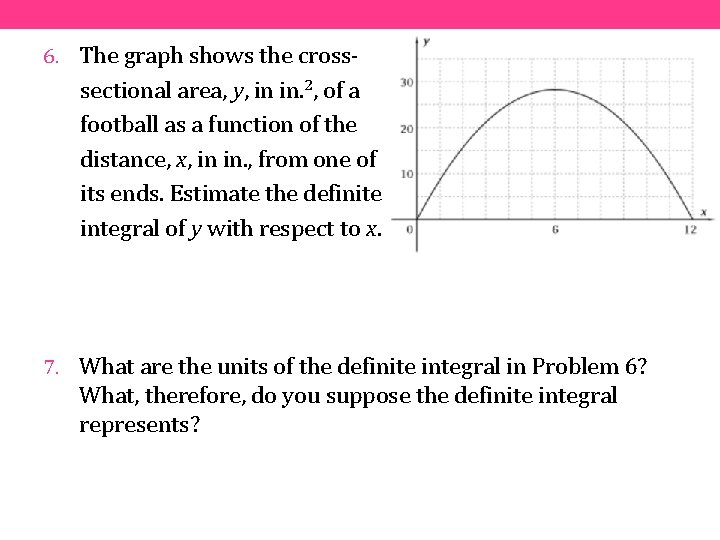
6. The graph shows the cross- sectional area, y, in in. 2, of a football as a function of the distance, x, in in. , from one of its ends. Estimate the definite integral of y with respect to x. 7. What are the units of the definite integral in Problem 6? What, therefore, do you suppose the definite integral represents?

- Slides: 22