Accelerator Physics Coupling Control G A Krafft Old

Accelerator Physics Coupling Control G. A. Krafft Old Dominion University Jefferson Lab Lecture 9 Graduate Accelerator Physics Fall 2017

Time Dependence For an oscillation starting in x-direction Graduate Accelerator Physics Fall 2017

Qualitatively • Oscillation energy migrates x→y→x • Period for a complete cycle is Becomes longer the weaker the coupling (→compensation) • If un-coupled oscillation periods different Eigenvectors no longer pure symmetric and antisymmetric but “migration” is fairly generic behavior Graduate Accelerator Physics Fall 2017

Energy and Mode Invariants • In normal mode coordinates • (uncoupled) Hamiltonian is and is a constant of the motion. • So are the individual mode excitation amplitudes Graduate Accelerator Physics Fall 2017

Solutions Again • In normal mode coordinates • betas and deltas from • back in coupled variables excitation looks like Graduate Accelerator Physics Fall 2017

Wiedemann Discussion • 1 -D know two pseudoharmonic trajectories • z-derivative Graduate Accelerator Physics Fall 2017

• Express ellipse functions in terms of solutions • Change in phase (phase advance) is Graduate Accelerator Physics Fall 2017

Transfer Matrix • General solution • Initial conditions • Transfer matrix Graduate Accelerator Physics Fall 2017

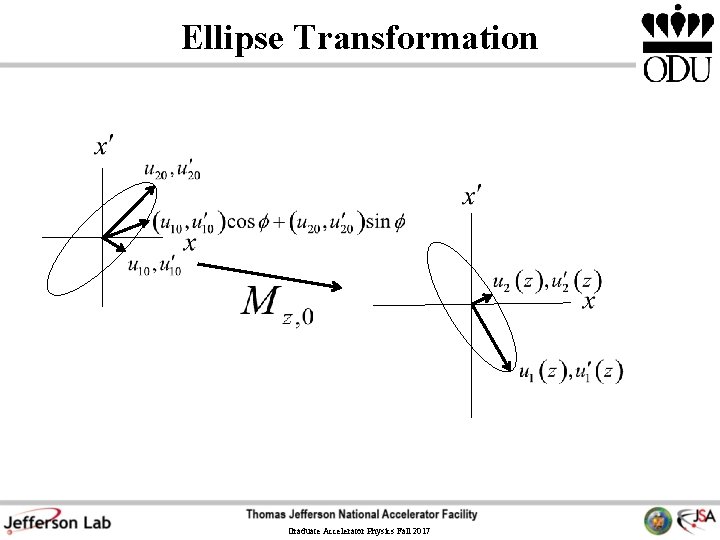
Ellipse Transformation Graduate Accelerator Physics Fall 2017

In 2× 2 D • As in toy problem, invariant is hyperellipsoid in 4 D. Parameterize individual state points as • Compared to uncoupled case have twice the number of matrix elements. Need twice the number of solutions. Wiedemann chooses Graduate Accelerator Physics Fall 2017

As Before Graduate Accelerator Physics Fall 2017

Convert Fundamental Solutions • Convert usual phase space variables • Points of hyper-ellipsoid Graduate Accelerator Physics Fall 2017

Beam size • Set all derivatives zero • Projected Ellipse Graduate Accelerator Physics Fall 2017

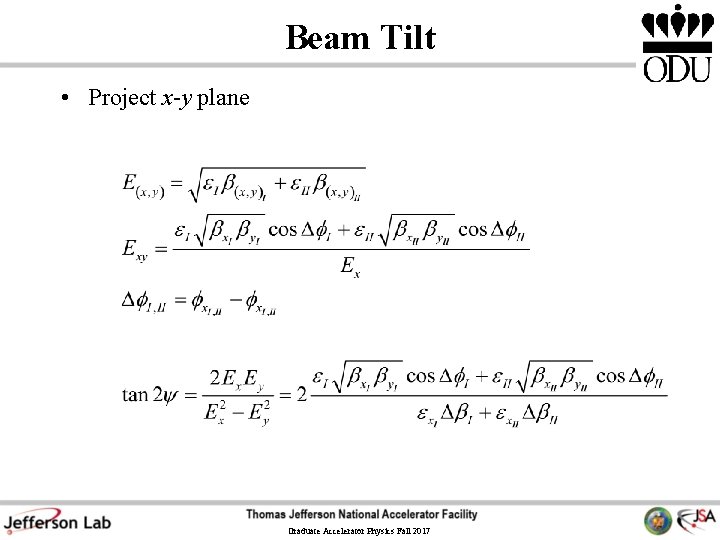
Beam Tilt • Project x-y plane Graduate Accelerator Physics Fall 2017

Beam sizes Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 7 - Coupled Betatron Motion I USPAS, Fort Collins, CO, June 10 -21, 2013 15

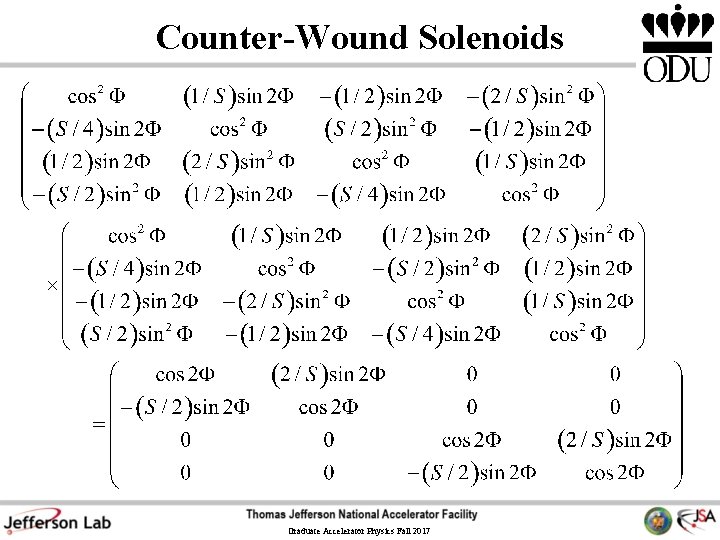
Decoupling • Counter Wound Solenoids • Compensating Solenoids or Skew Quads – Jefferson Lab – MEIC Application – Rings • Flat Beams Graduate Accelerator Physics Fall 2017

Counter-Wound Solenoids Graduate Accelerator Physics Fall 2017

Axisymmetric Rotational Distribution Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 18

Axisymmetric Rotational Distribution Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 19

Axisymmetric Rotational Distribution Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 20

Axisymmetric Rotational Distribution Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 21

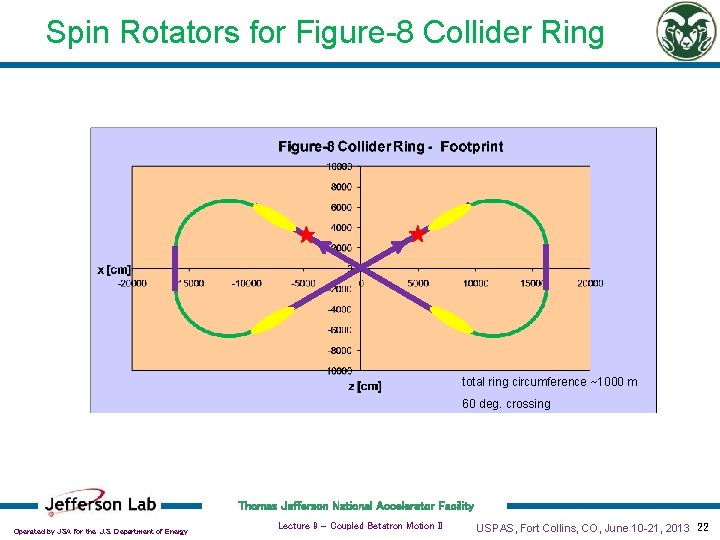
Spin Rotators for Figure-8 Collider Ring total ring circumference ~1000 m 60 deg. crossing Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 22

0 -0. 15 DISP_X&Y[m] BETA_X&Y[m] 0. 15 15 Spin Rotator - Ingredients… 230 BETA_X BETA_Y DISP_X Arc end DISP_Y 320 BL = 11. 9 Tesla m 8. 8 0 BL = 28. 7 Tesla m 4. 4 0 Spin rotator ~ 46 m Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 23

15 5 Locally Decoupled Solenoid Pair 0 0 0 BETA_X&Y[m] BL = 28. 7 Tesla m BETA_1 X BETA_2 Y solenoid 4. 16 m BETA_1 Y BETA_2 X 17. 9032 solenoid 4. 16 m decoupling quad insert M= C 0 0 -C Hisham Sayed, Ph. D Thesis ODU, 2011 Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 24

15 1 Locally Decoupled Solenoid Pair 0 -1 DISP_X&Y[m] BETA_X&Y[m] BL = 28. 7 Tesla m 0 BETA_X BETA_Y solenoid 4. 16 m DISP_X DISP_Y 17. 9032 solenoid 4. 16 m decoupling quad insert M= C 0 0 -C Hisham Sayed, Ph. D Thesis ODU, 2011 Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 25

Universal Spin Rotator Optics 1 0 -1 DISP_X&Y[m] BETA_X&Y[m] 30 5 Ge. V 288 BETA_X BETA_Y DISP_X DISP_Y 374 BL = 11. 9 Tesla m 8. 8 0 BL = 28. 7 Tesla m 4. 4 0 Spin rotator ~ 46 m Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 26

Ionization Cooling in an Axially Symmetric Channel Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 27

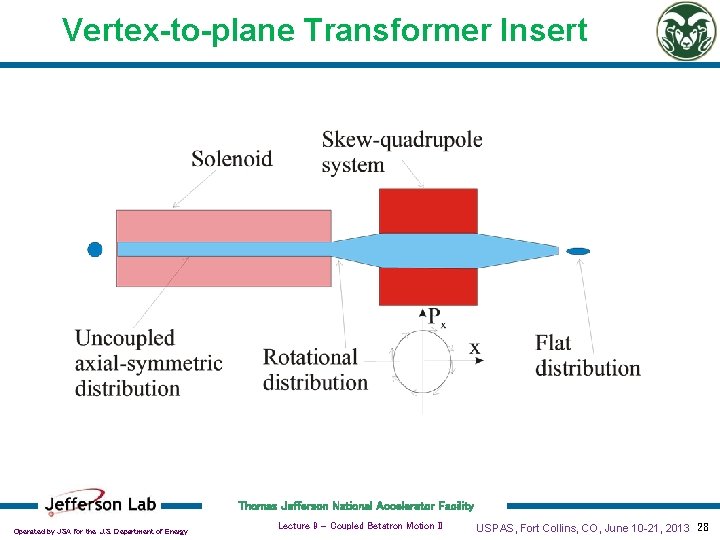
Vertex-to-plane Transformer Insert Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 28

Vertex-to-plane Transformer Insert Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 29

Vertex-to-plane Transformer Insert Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 30

Ax Ay Alpha. XY BETA_2 X 2. 62647 5 1 0 Alpha. XY[-1, +1] PHASE/(2*PI) -1 0 Betatron size X&Y[cm] 0 0 0 2. 62647 0 BETA_1 X BETA_2 Y BETA_1 Y BETA_2 X Q_1 Q_2 Teta 1 Teta 2 2. 62647 0 0. 5 BETA_1 Y 0 BETA_2 Y 1 BETA_1 X 1 0 0. 5 0 BETA_X&Y[m] 5 0 1 Vertex-to-plane Transformer Insert 2. 62647 Thomas Jefferson National Accelerator Facility Operated by JSA for the U. S. Department of Energy Lecture 9 - Coupled Betatron Motion II USPAS, Fort Collins, CO, June 10 -21, 2013 31

Northern Illinois Center for Accelerator and Detector Development Generation and Dynamics of Magnetized Beams for High-Energy Electron Cooling* Philippe Piot, Department of Physics and Northern Illinois Center for Accelerator & Detector Development, Northern Illinois University, De. Kalb IL 60115 Accelerator Physics Center, Fermi National Accelerator Laboratory, Batavia IL 60510 Yin-e Sun, Advanced Photon Source, Argonne National Laboratory, Argonne IL 60439 International Workshop on Accelerator Science & Technologies for future electron-ion colliders (EIC’ 14), Jefferson Lab, March 17 -21, 2014 *sponsored by the DOE awards DE-FG 02 -08 ER 41532 to Northern Illinois University and DE-AC 02 -07 CH 11359 to the Fermi Research Alliance LLC.

Outline • Introduction • Features and parameterization of magnetized beams • Formation of magnetized bunches: – methods and limitations, – experiments in rf gun. • Transport and Manipulation: – transverse matching, – longitudinal manipulations, – decoupling into flat beams. • Outlook P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 33

Required Electron-Beam Parameters • Cooling interaction time (magnetized) (not magnetized) (magnetized) • magnetized cooling less dependent on e- beam transverse emittance (to what extent? ) (not magnetized) • electron-cooling accelerator provides beam eventually matched to coolingsolenoid section P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 34

• low-energy coolers: – lattice (bends) embedded in magnetic fields, – based on DC electron sources, – no further acceleration or bunching, needed. • high-energy coolers: e. g. see I. Ben-Zvi, et al. , Proc. PAC 2001, p. 48 (2001) e. g. see S. Nagaitsev, et al, PRL 96, 044801 (2006) Cooler configurations – medium energies required (50 -100 Me. V), – acceleration in SCRF linac bunching – lumped solenoidal fields matching 300 ke. V, 3 A cooler produced by Budker INP for IMP, Lanzhou (China) early concept for RHIC e-cooling P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 35

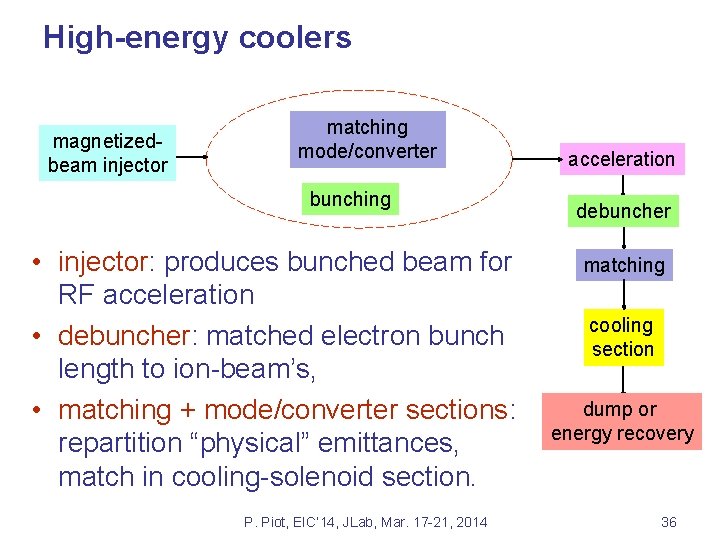
High-energy coolers magnetizedbeam injector matching mode/converter bunching • injector: produces bunched beam for RF acceleration • debuncher: matched electron bunch length to ion-beam’s, • matching + mode/converter sections: repartition “physical” emittances, match in cooling-solenoid section. P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 acceleration debuncher matching cooling section dump or energy recovery 36

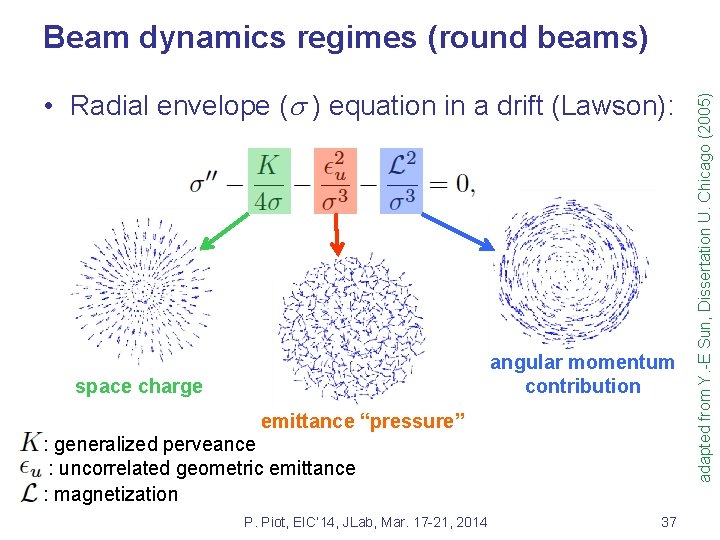
• Radial envelope (s ) equation in a drift (Lawson): angular momentum contribution space charge emittance “pressure” : generalized perveance : uncorrelated geometric emittance : magnetization P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 37 adapted from Y. -E Sun, Dissertation U. Chicago (2005) Beam dynamics regimes (round beams)

Features & Parameterization • possible parameterization of coupled motion between 2 degrees of freedom has been extensively discussed; see: – D. A. Edwards and L. C. Teng, IEEE Trans. Nucl. Sci. 20, 3, pp. 885 -889 (1973). – I. Borchardt, E. Karantzoulis, H. Mais, G. Ripken, DESY 87 -161 (1987). – V. Lebedev, S. A. Bogacz, Ar. Xi. V: 1207. 5526 (2007). – A. Burov, S. Nagaitsev, A. Shemyakin, Ya. Derbenev, PRSTAB 3, 094002 (2000). – A. Burov, S. Nagaitsev, Ya. Derbenev, PRE 66, 016503 (2002). • Simpler description that provides the necessary insights. . P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 38

A simple description of coupled motion • Consider the 4 x 4 beam matrix where • Introduce the “correlation” matrix: • Beam matrix takes the form: • The correlation subjects to as transforms • C provides information on the coupling only. P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 39

• At a waist, the matrix of a magnetized (round) beam is where and the magnetization is • The eigen-emittances of this beam matrix are: where • the eigen-emittances can be mapped into “physical” emittances using a skewed beamline K. -J. Kim, PRSTAB 6, 104002 (2003) D. A. Edwards, unpublished (2001) Beam matrix for a round magnetized beam decoupling when P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 40

Formation of magnetized bunches • Cathode immersed in an axial B field • Sheet beams at birth (with subsequent flat-to-round beam converter) – shaped cathode, – line-laser focus – Nonlinear optics (speculative) mode converter Y. Derbenev, University of Michigan report UM-HE-98 -04 (1998) G. Florentini, et al. , Proc. PAC 95, p. 973 (1996) P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 41

Cathode in a magnetic field • electrons born in an axial B field • upon exit of solenoid field ( becomes purely kinetic. P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 CAM ): CAM 42

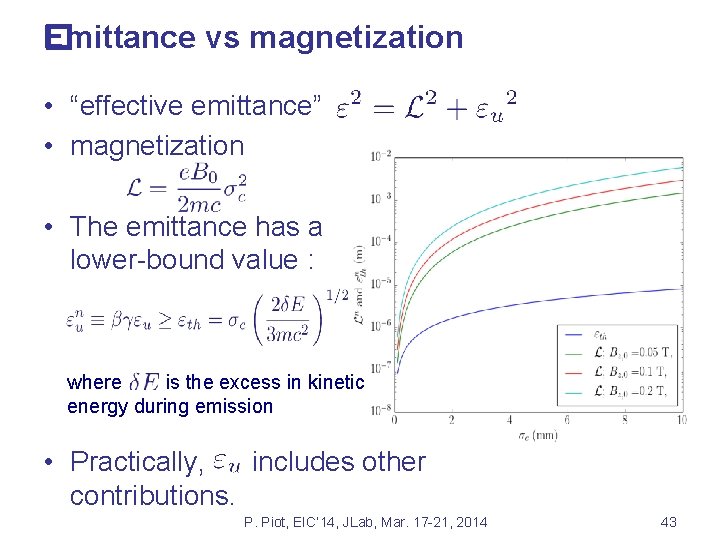
Emittance vs magnetization � • “effective emittance” • magnetization • The emittance has a lower-bound value : where is the excess in kinetic energy during emission • Practically, includes other contributions. P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 43

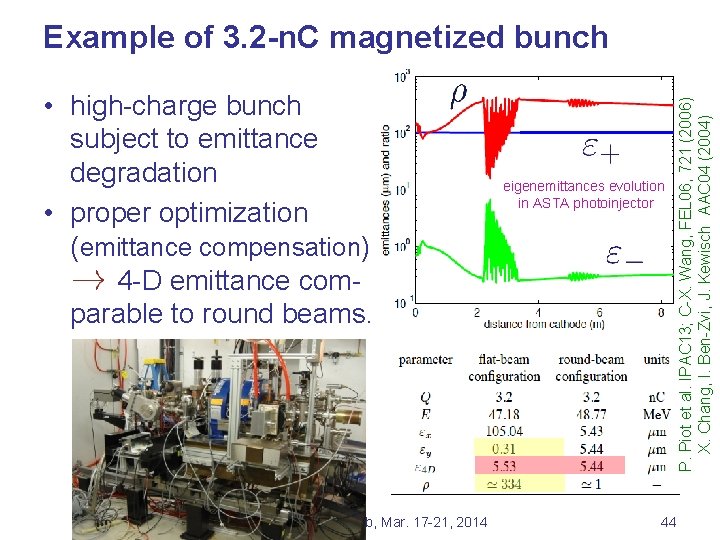
• high-charge bunch subject to emittance degradation • proper optimization (emittance compensation) 4 -D emittance comparable to round beams. P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 eigenemittances evolution in ASTA photoinjector P. Piot et al. IPAC 13; C-X. Wang, FEL 06, 721 (2006) X. Chang, I. Ben-Zvi, J. Kewisch AAC 04 (2004) Example of 3. 2 -n. C magnetized bunch 44

Y. -E Sun et al, PRSTAB 7, 123501 (2004) Measuring (kinetic) angular momentum • Kinetic angular momentum can be measured using a slit technique (similar to emittance) beam at slits beam at observation point • The beam’s average angular momentum is given by : rms beam size at slit (1) and observation screen (2), : axial momentum : drift length between locations (1) and (2). P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 45

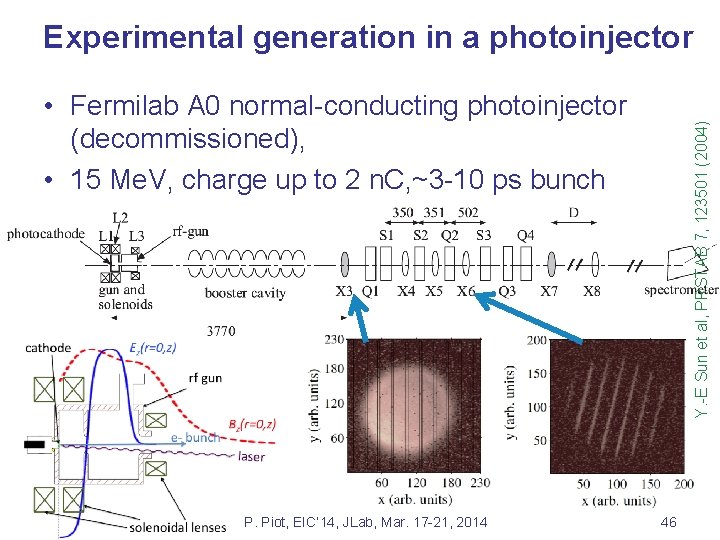
Experimental generation in a photoinjector P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 Y. -E Sun et al, PRSTAB 7, 123501 (2004) • Fermilab A 0 normal-conducting photoinjector (decommissioned), • 15 Me. V, charge up to 2 n. C, ~3 -10 ps bunch • main focus was conversion to flat beams 46

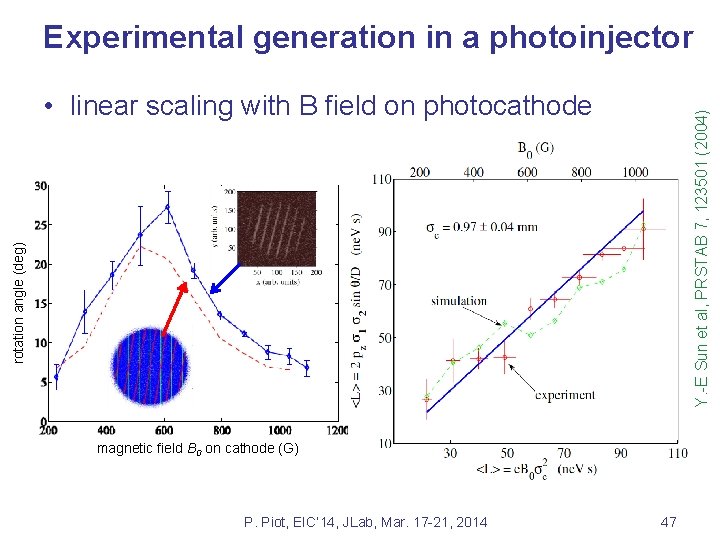
Experimental generation in a photoinjector rotation angle (deg) Y. -E Sun et al, PRSTAB 7, 123501 (2004) • linear scaling with B field on photocathode magnetic field B 0 on cathode (G) P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 47

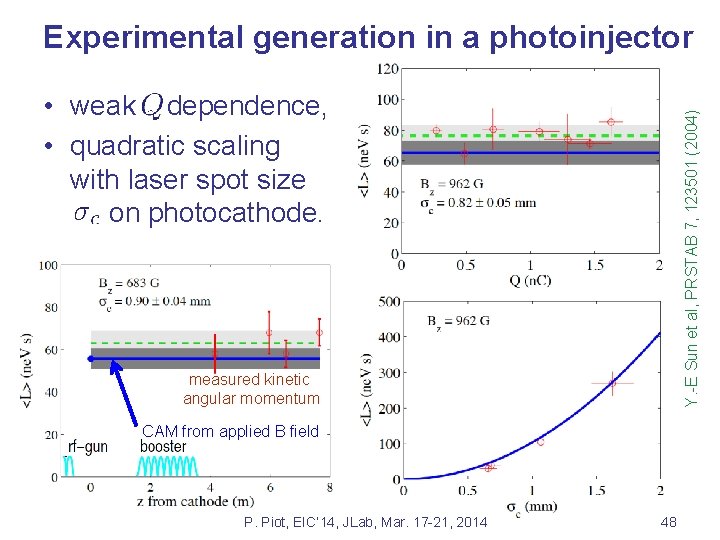
Experimental generation in a photoinjector Y. -E Sun et al, PRSTAB 7, 123501 (2004) • weak dependence, • quadratic scaling with laser spot size on photocathode. measured kinetic angular momentum CAM from applied B field P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 48

• Transport of magnetized bunches while preserving is challenging, • Use of round-to-flat beam transformer to convert into uncoupled (flat) beam eigen-emittances maps into “physical” transverse emittances: P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 R. Brinkmann et al. , PRSTAB 4, 053501 (2001) Y. Derbenev, University of Michigan report UM-HE-98 -04 (1998) Decoupling into flat (ex/ey≠ 1) beam 49

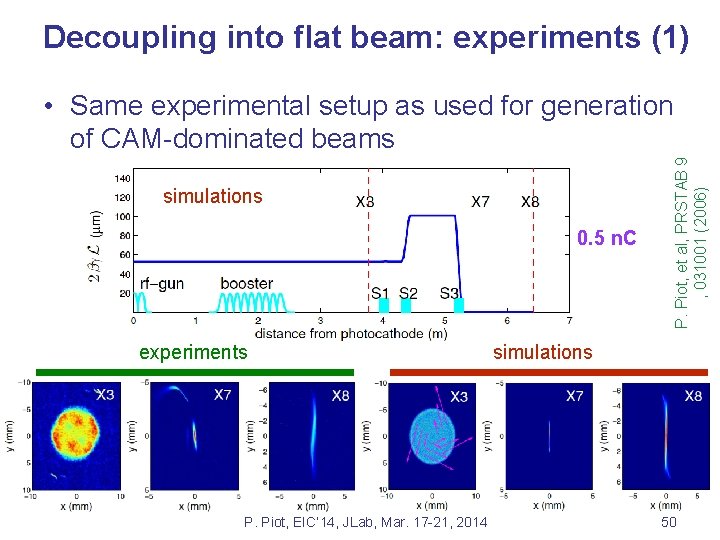
Decoupling into flat beam: experiments (1) simulations 0. 5 n. C experiments P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 P. Piot, et al, PRSTAB 9 , 031001 (2006) • Same experimental setup as used for generation of CAM-dominated beams simulations 50

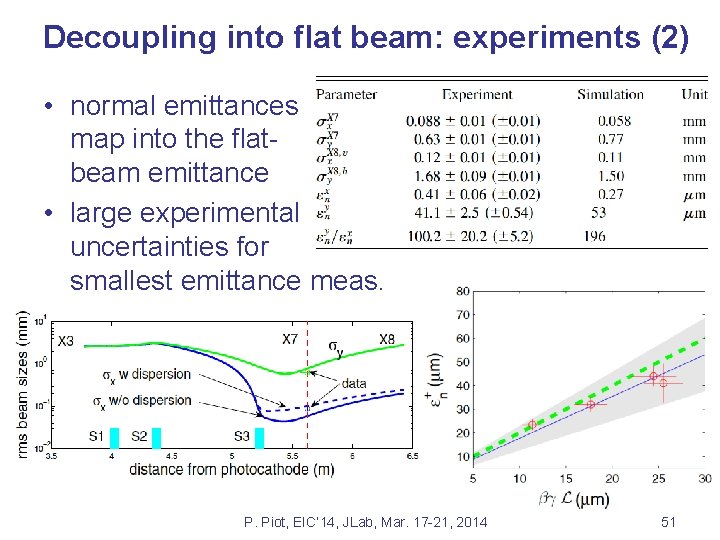
Decoupling into flat beam: experiments (2) • normal emittances map into the flatbeam emittance • large experimental uncertainties for smallest emittance meas. P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 51

Outlook + open questions • magnetized beam from a SCRF gun: – flux concentrator around cathode? – flat beam at cathode [J. Rosenzweig, PAC 93 showed ( , )=(95, 4. 5) mm] • needed and ? and limit on 4 -D emittance? • planned future experiment at ASTA P. Piot, EIC’ 14, JLab, Mar. 17 -21, 2014 52