Acceleration Polygon for a Fourbar Introduction Acceleration Polygon

Acceleration Polygon for a Four-bar Introduction Acceleration Polygon for a Four-bar Mechanism This presentation shows how to construct the acceleration polygon for a fourbar mechanism. It is assumed that the dimensions for the links are known and the analysis is being performed at a given (known) configuration. Since the four-bar has one degree-of-freedom, the angular velocity and acceleration of one of the links must be given as well. As an example, for the four-bar shown, we first construct the velocity polygon. Then we will learn: 1. How to construct the acceleration polygon shown on the right 2. How to extract acceleration information from the polygon A A B ABA ω2 α 2 O 4 O 2 �B P. Nikravesh, AME, U of A AA AB OA

Example Acceleration Polygon for a Four-bar B Example This example shows us how to construct the acceleration polygon for a typical four-bar, such as the one shown on this slide. It is assumed that: all the lengths are known and the four-bar is being analyzed at the configuration shown; the angular velocity and acceleration of the crank are given as well. P. Nikravesh, AME, U of A A ω2 α 2 O 4 O 2

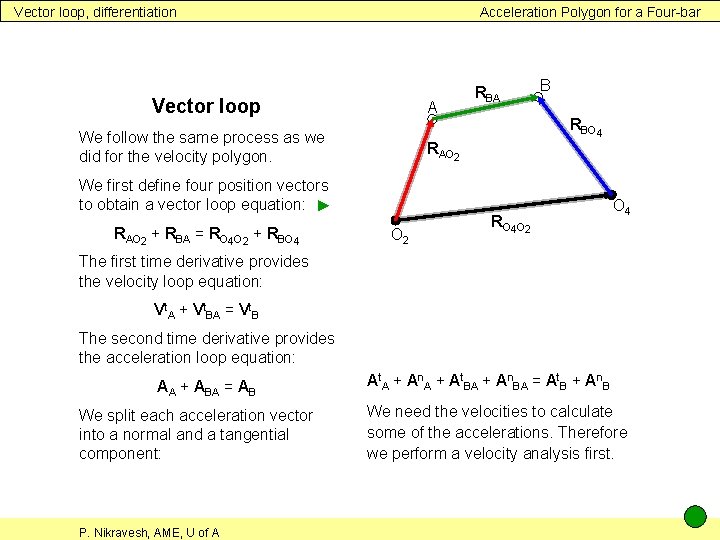
Vector loop, differentiation Acceleration Polygon for a Four-bar Vector loop A We follow the same process as we did for the velocity polygon. B RBO 4 RAO 2 We first define four position vectors to obtain a vector loop equation: ► RAO 2 + RBA = RO 4 O 2 + RBO 4 RBA O 2 RO 4 O 2 O 4 The first time derivative provides the velocity loop equation: Vt. A + Vt. BA = Vt. B The second time derivative provides the acceleration loop equation: AA + ABA = AB We split each acceleration vector into a normal and a tangential component: P. Nikravesh, AME, U of A At. A + An. A + At. BA + An. BA = At. B + An. B We need the velocities to calculate some of the accelerations. Therefore we perform a velocity analysis first.

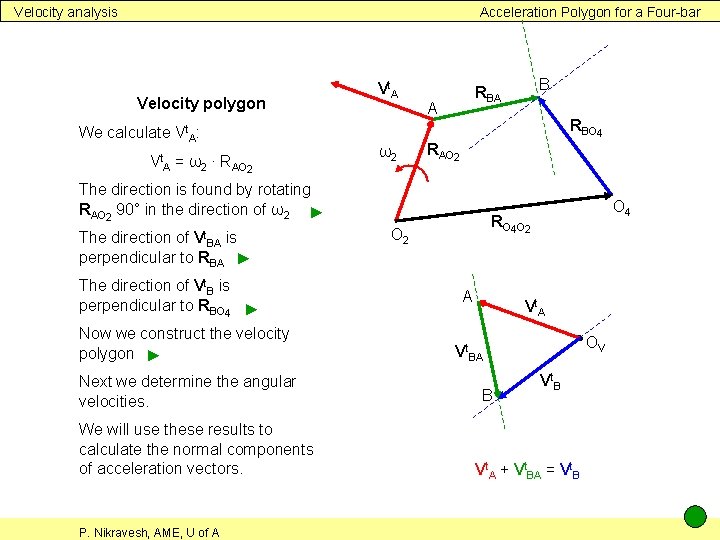
Velocity analysis Acceleration Polygon for a Four-bar Velocity polygon We calculate Vt. A: Vt. A = ω2 ∙ RAO 2 Vt. A ω2 A RBO 4 RAO 2 The direction is found by rotating RAO 2 90° in the direction of ω2 ► Vt. BA The direction of is perpendicular to RBA ► The direction of Vt. B is perpendicular to RBO 4 ► Now we construct the velocity polygon ► Next we determine the angular velocities. We will use these results to calculate the normal components of acceleration vectors. P. Nikravesh, AME, U of A B RBA O 4 RO 4 O 2 A Vt. A OV Vt. BA B Vt. A + Vt. BA = Vt. B

Angular velocities Acceleration Polygon for a Four-bar Angular velocities The absolute value of the angular velocities are computed as: Vt. A ω2 A B RBA ω3 RBO 4 RAO 2 ω4 ω3 = Vt. BA ∕ RBA ω4 = Vt. B ∕ RBO 4 RBA has to be rotated 90° cw to head in the direction of Vt. BA. Therefore ω3 is cw ► RBO 4 has to be rotated 90° ccw to head in the direction of Vt. B. Therefore ω4 is ccw ► We will use these results to calculate accelerations. P. Nikravesh, AME, U of A O 4 RO 4 O 2 A Vt. A OV Vt. BA B Vt. B

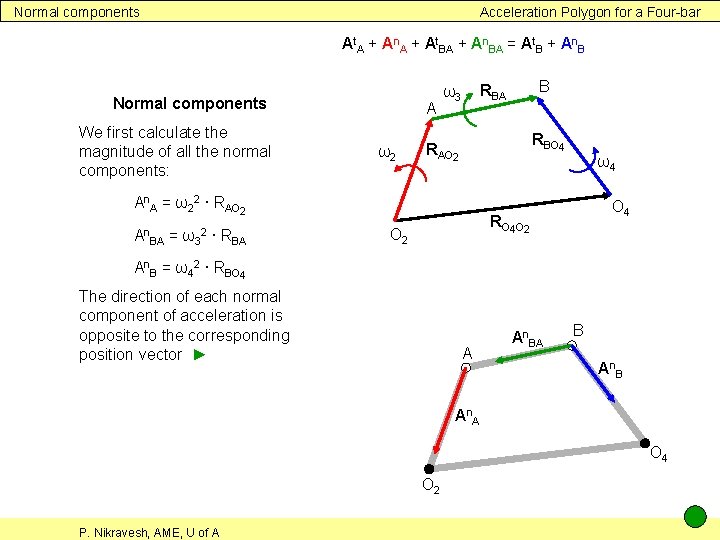
Normal components Acceleration Polygon for a Four-bar At. A + An. A + At. BA + An. BA = At. B + An. B Normal components We first calculate the magnitude of all the normal components: A ω2 RBO 4 RAO 2 An. A = ω22 ∙ RAO 2 An BA = ω3 ∙ RBA 2 B RBA ω3 ω4 O 4 RO 4 O 2 An. B = ω42 ∙ RBO 4 The direction of each normal component of acceleration is opposite to the corresponding position vector ► A An. BA B An A O 4 O 2 P. Nikravesh, AME, U of A

Tangential components Acceleration Polygon for a Four-bar At. A + An. A + At. BA + An. BA = At. B + An. B Tangential components A We first calculate the magnitude of At. A: At. A = α 2 ∙ RAO 2 The direction is found by rotating RAO 2 90° in the direction of α 2 ► B RBA RBO 4 RAO 2 α 2 O 4 RO 4 O 2 We also know that At. BA is on an axis perpendicular to RBA ► Similarly we know that At. B is on an axis perpendicular to RBO 4 ► At. A A An. BA B An A O 4 O 2 P. Nikravesh, AME, U of A

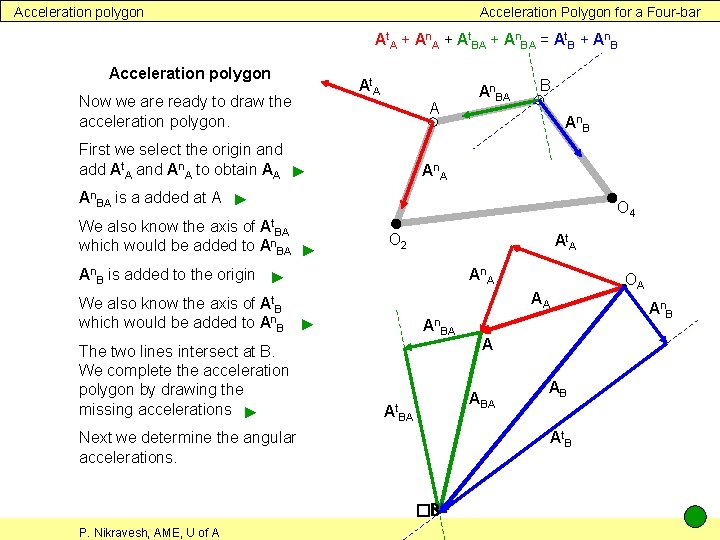
Acceleration polygon Acceleration Polygon for a Four-bar At. A + An. A + At. BA + An. BA = At. B + An. B Acceleration polygon At. A Now we are ready to draw the acceleration polygon. A First we select the origin and add At. A and An. A to obtain AA ► An. BA B An A An. BA is a added at A ► We also know the axis of which would be added to At. BA An. BA O 4 ► O 2 At. A An. B is added to the origin ► AA We also know the axis of At. B which would be added to An. B ► The two lines intersect at B. We complete the acceleration polygon by drawing the missing accelerations ► An. BA At. BA An B A AB At. B Next we determine the angular accelerations. �B P. Nikravesh, AME, U of A OA

Angular accelerations Acceleration Polygon for a Four-bar Angular accelerations The absolute values of the angular accelerations are computed as: α 3 = At. BA ∕ RBA α 4 = At. B ∕ RBO 4 A α 3 α 4 α 2 O 4 RO 4 O 2 At. A An A OA AA RBO 4 has to be rotated 90° ccw to head in the direction of At. B. Therefore α 4 is ccw ► P. Nikravesh, AME, U of A RBO 4 RAO 2 RBA has to be rotated 90° cw to head in the direction of At. BA. Therefore α 3 is cw ► This completes the acceleration analysis of this four-bar. B RBA An B An. BA At. BA AB At. B