Acceleration due to gravity Earth Acceleration due to





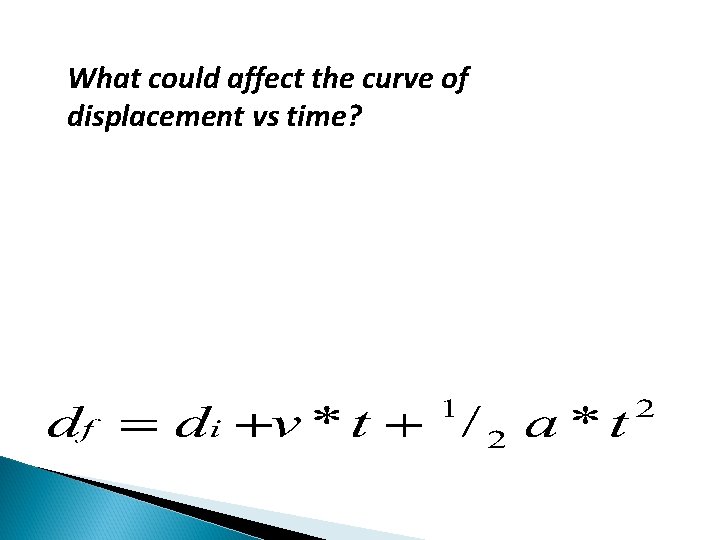
































- Slides: 61

Acceleration due to gravity (Earth)

Acceleration due to gravity (Earth) • Treated as a constant near the Earth • 9. 81 m/sec^2 = 981 cm/sec^2

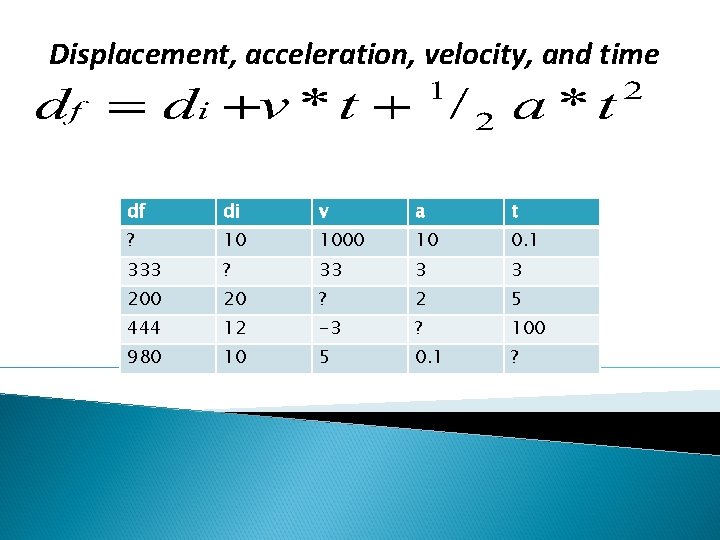
Displacement, velocity, and time Units? m/sec = m/sec

Displacement versus time 30 25 20 displacement 15 v 10 5 0 0 2 4 6 time 8 10 12 14

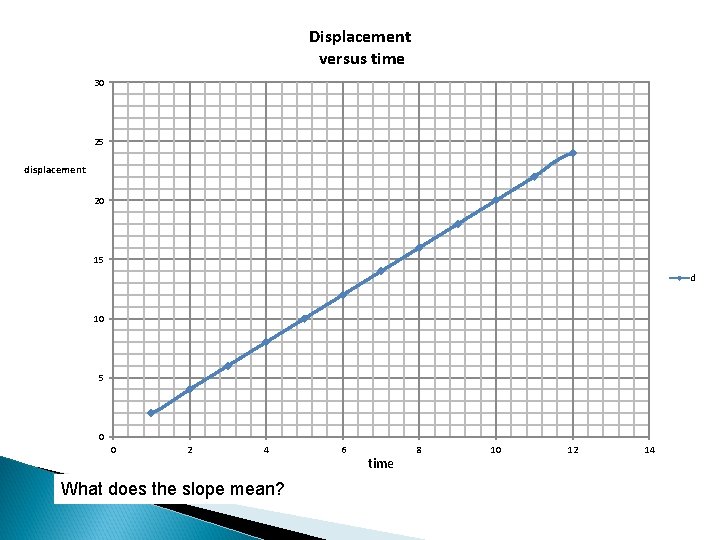
Displacement versus time 30 25 displacement 20 15 d 10 5 0 0 2 4 What does the slope mean? 6 time 8 10 12 14

Velocity, acceleration, and time m/sec = m/sec-2 * sec m/sec-2 = m/sec / sec

Velocity versus time 30 25 20 velocit 15 v 10 5 0 0 2 4 Assume constant acceleration 6 time 8 10 12 14

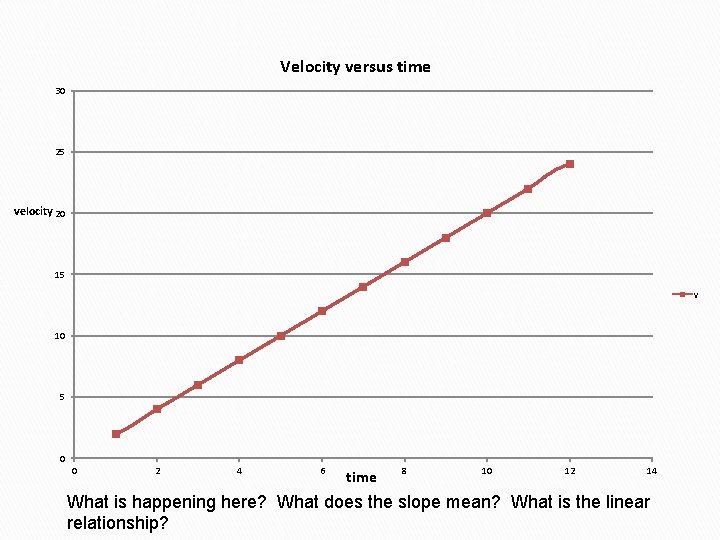
Velocity versus time 30 25 velocity 20 15 v 10 5 0 0 2 4 6 time 8 10 12 14 What is happening here? What does the slope mean? What is the linear relationship?

Displacement, acceleration, and time

Displacement versus time 30 25 20 velocit 15 v 10 5 0 0 2 4 Assume constant acceleration 6 time 8 10 12 14

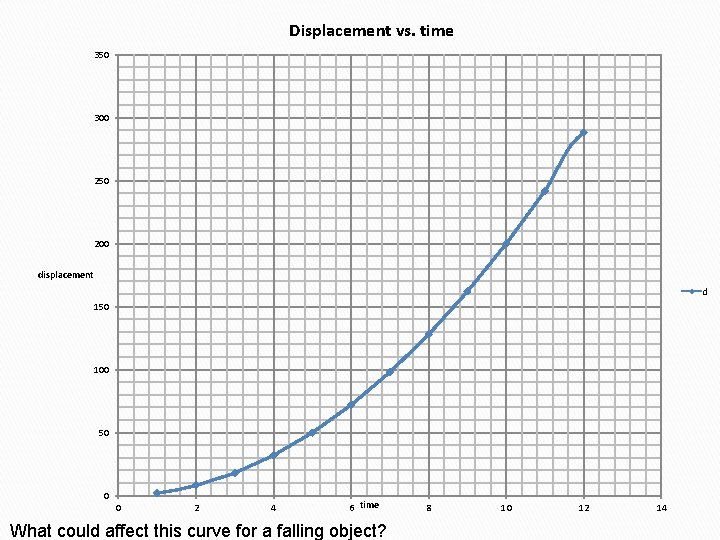
Displacement vs. time 350 300 250 200 displacement d 150 100 50 0 0 2 4 6 time What could affect this curve for a falling object? 8 10 12 14
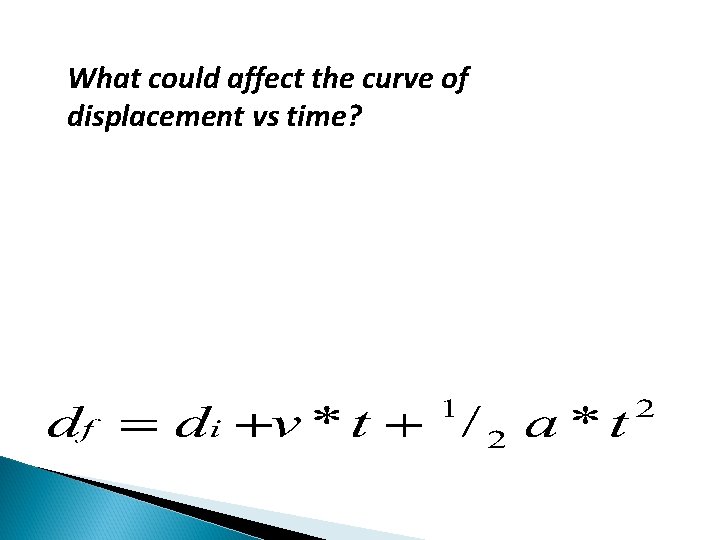
What could affect the curve of displacement vs time?

What could affect the curve of displacement vs time? • Initial displacement? • Initial velocity? • Wind resistance? • Mass? • Size?

22. An object shot straight up rises for 7. 0 sec before it reaches its maximum height. A second object falling from rest takes 7 sec to reach the ground. Compare the displacements of the objects. (Start Per 7)

23. Describe the changes in the velocity of a ball thrown straight up into the air. Describe the changes in the acceleration.

24. The value of g on the moon is 1/6 of its value on Earth. Will a ball dropped by an astronaut hit the surface of the moon with a smaller, equal, or larger speed than that of a ball dropped the same height on Earth?

26. One rock is dropped from a cliff, the other thrown upwards from the top of the cliff. They both land at the bottom of the cliff. Which has a greater velocity at landing? Which has a greater acceleration? Which arrives first?

Given: A ball, initially at rest, is dropped. Assuming it is near the surface of the earth, how far does it fall in 2 seconds? 4? 100? What is its final velocity?

Given: A ball, initially at rest, is dropped. Assuming it is near the surface of the earth, how far does it fall in 2 seconds? 4? 100? d = ½ a t^2, where a = 9. 8 m/sec^2 What is its final velocity?

Given: A ball, initially at rest, is dropped. Assuming it is near the surface of the earth, how far does it fall in 2 seconds? 4? 100? d = ½ * a * t^2, where a = 9. 81 m/sec^2 What is its final velocity? V = a * t, where a = 9. 81 m/sec^2 and t is found above

A ball falls from rest for a distance of 6 m. How far will it fall in the next 0. 1 sec?

A ball falls from rest for a distance of 6 m. How far will it fall in the next 0. 1 sec? Find t from d = (1/2)at^2 Find d from d = (1/2)a(t+0. 1)^2

Displacement, velocity, acceleration, and time

Optional: Displacement, velocity, and time df d 0 v t 100 10 1000 ? 10 15 ? 100 2 ? 12 -3 10 32 1 ? 0. 1 50 ? 500 10 ? 22 44 6

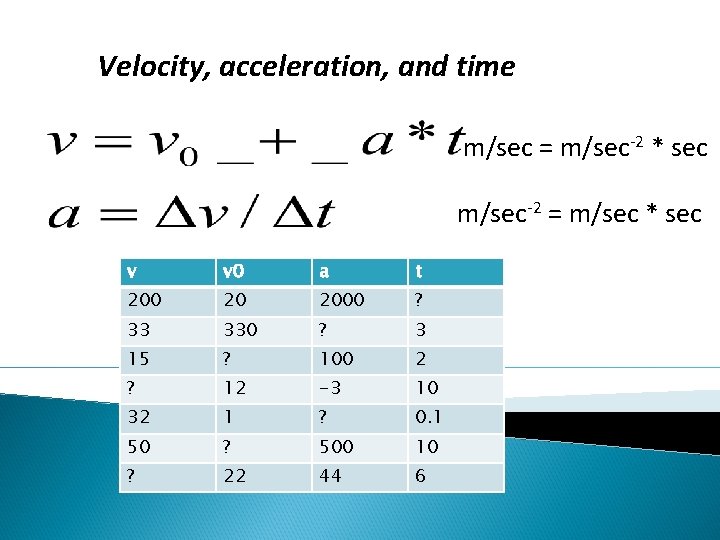
Velocity, acceleration, and time m/sec = m/sec-2 * sec m/sec-2 = m/sec * sec v v 0 a t 200 20 2000 ? 33 330 ? 3 15 ? 100 2 ? 12 -3 10 32 1 ? 0. 1 50 ? 500 10 ? 22 44 6

Displacement, acceleration, and time d a t ? 9. 8 1000 100 980 ? 15 ? 100 ? 12 3 32 1 ? 500 ? 22 44

Displacement, acceleration, velocity, and time df di v a t ? 10 1000 10 0. 1 333 ? 33 3 3 200 20 ? 2 5 444 12 -3 ? 100 980 10 5 0. 1 ?

Displacement, acceleration, and velocity Position, velocity and acceleration when t is unknown. vf 2 = vi 2 + 2 * a * d Vf vi a d 100 10 ? 1000 100 20 1000 ? 15 3 ? 100 ? 6 12 -3 32 0 1 ? 50 5 ? 500 ? 11 22 44

Example 1: Calculating Distance A stone is dropped from the top of a tall building. After 3. 00 seconds of free-fall, what is the displacement, d of the stone? Data vf n/a vi 0 m/s d ? a=g t -9. 81 m/s 2 3. 00 s

Example 1: Calculating Distance Since vi = 0 we will substitute g for a and get: d = ½ gt 2 d = ½ (-9. 81 m/s 2)(3. 00 s)2 d = -44. 1 m

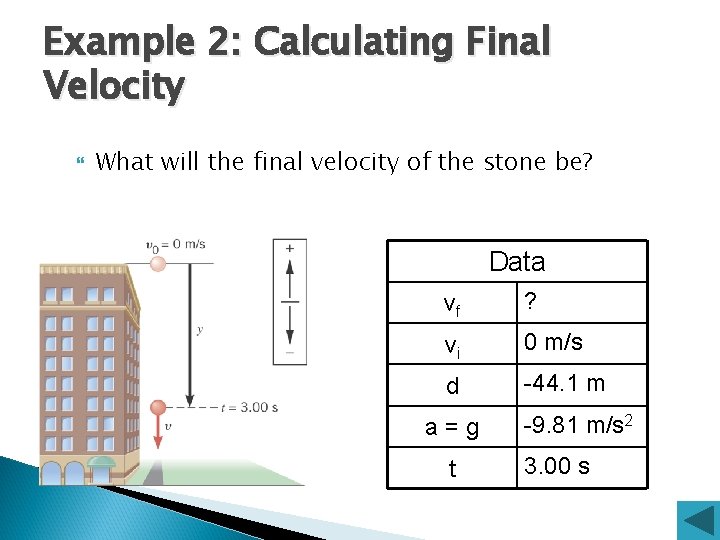
Example 2: Calculating Final Velocity What will the final velocity of the stone be? Data vf ? vi 0 m/s d -44. 1 m a=g t -9. 81 m/s 2 3. 00 s

Example 2: Calculating Final Velocity Again, since vi = 0 we will substitute g for a and get: vf = gt vf = (-9. 81 m/s 2)(3. 00 s) vf = -29. 4 m/s Or, we can also solve the problem with: vf 2 = vi 2 + 2 a d, where vi = 0 vf = [(2(-9. 81 m/s 2)(44. 1 m)]1/2 vf = -29. 4 m/s

Example 3: Determining the Maximum Height (per 6) How high will the coin go? Data vf 0 m/s vi 5. 00 m/s d ? a=g t -9. 81 m/s 2 ?

Example 3: Determining the Maximum Height Since we know the initial and final velocity as well as the rate of acceleration we can use: vf 2 = vi 2 + 2 a d Since Δd = Δy we can algebraically rearrange the terms to solve for Δy.

Example 4: Determining the Total Time in the Air How long will the coin be in the air? Data vf 0 m/s vi 5. 00 m/s d 1. 28 m a=g t -9. 81 m/s 2 ?

Example 4: Determining the Total Time in the Air Since we know the initial and final velocity as well as the rate of acceleration we can use: vf = vi + aΔt, where a = g Solving for t gives us: Since the coin travels both up and down, this value must be doubled to get a total time of 1. 02 s

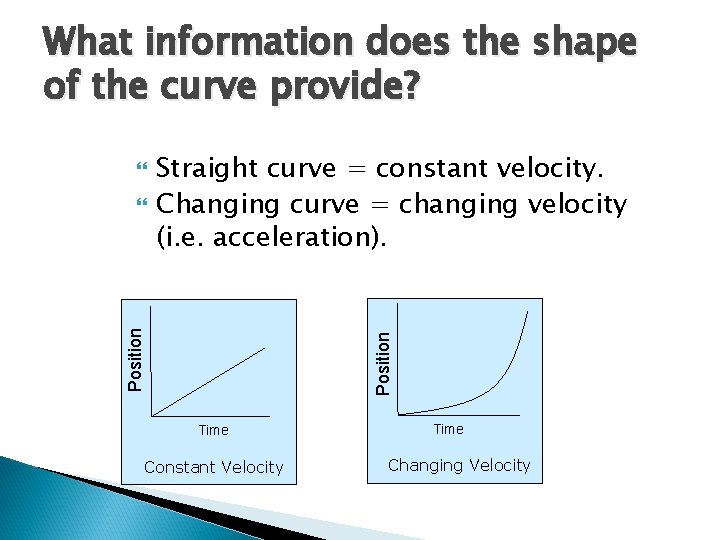
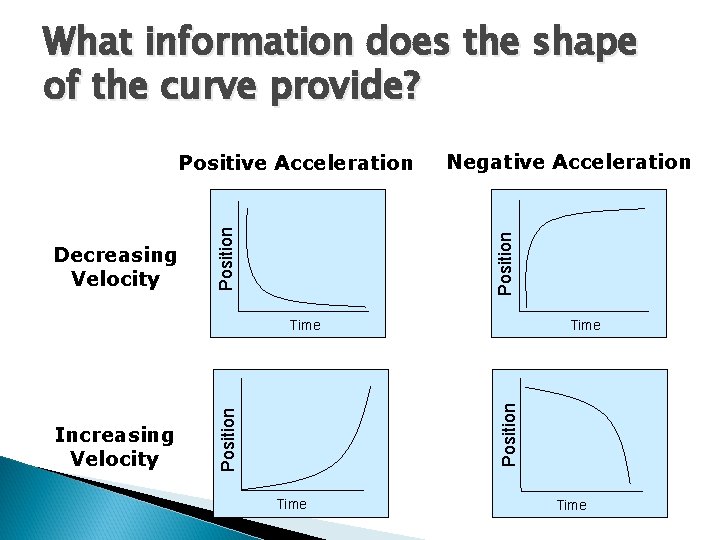
What information does the shape of the curve provide? Position Straight curve = constant velocity. Changing curve = changing velocity (i. e. acceleration). Time Constant Velocity Time Changing Velocity

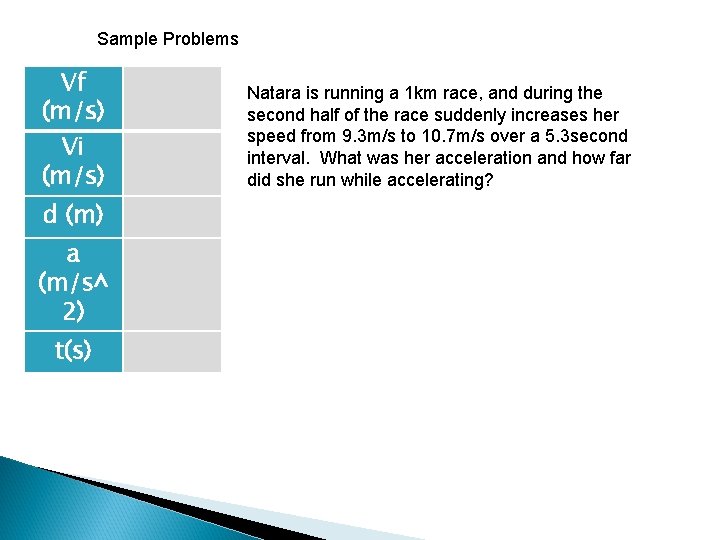
Sample Problems Vf (m/s) Vi (m/s) d (m) a (m/s^ 2) t(s) A horse rounds the curve at 11 m/s and accelerates to 17. 3 m/s. His acceleration is 1. 8 m/sec^2. How long does it take him to round the curve and what distance does he travel?

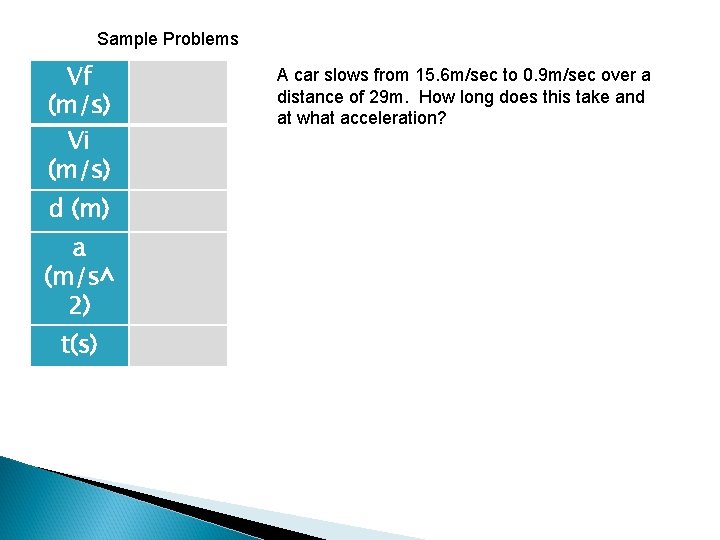
Sample Problems Vf (m/s) Vi (m/s) d (m) a (m/s^ 2) t(s) A car slows from 15. 6 m/sec to 0. 9 m/sec over a distance of 29 m. How long does this take and at what acceleration?

Sample Problems Vf (m/s) Vi (m/s) d (m) a (m/s^ 2) t(s) Natara is running a 1 km race, and during the second half of the race suddenly increases her speed from 9. 3 m/s to 10. 7 m/s over a 5. 3 second interval. What was her acceleration and how far did she run while accelerating?

Sample Problems Vf (m/s) Vi (m/s) d (m) a (m/s^ 2) t(s) Alex, while driving through the parking lot, brakes at 3 m/sec^2 over a distance of 47 m. What is his final velocity? For how long did he brake?

Sample Problems Vf (m/s) Vi (m/s) d (m) a (m/s^ 2) t(s) A train traveling at 5. 2 m/sec accelerates at 2. 3 m/sec^2 over a 4. 2 sec period. What is its final velocity? How far does it travel while accelerating?

Sample Problems Vf (m/s) Vi (m/s) d (m) a (m/s^ 2) t(s) Connor throws a bowling ball out the window of Planet Weird. Picture with a downward velocity of 14. 9 m/s. The ball falls 32 m in 9. 3 s. What is its final velocity and the acceleration due to gravity on planet Weird. Picture?

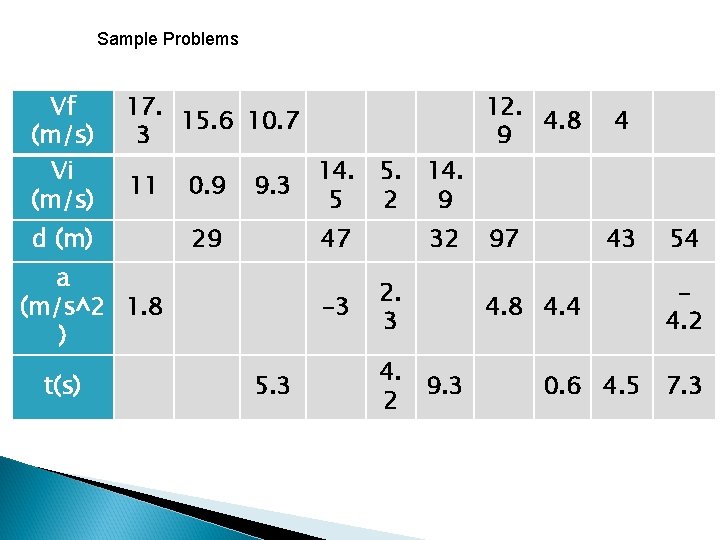
Sample Problems Vf (m/s) Vi (m/s) 12. 9 d (m) 97 a (m/s^ 2) 4. 8 t(s)

Sample Problems Vf (m/s) Vi (m/s) 4. 8 d (m) a (m/s^ 2) 4. 4 t(s) 0. 6

Sample Problems Vf (m/s) Vi (m/s) d (m) 4 43 a (m/s^ 2) t(s) 4. 5

Sample Problems Vf (m/s) Vi (m/s) 17. 15. 6 10. 7 3 d (m) 29 11 0. 9 9. 3 a (m/s^2 1. 8 ) t(s) 14. 5 5. 14. 2 9 47 32 -3 5. 3 2. 3 4. 9. 3 2 12. 4. 8 9 97 4 43 4. 8 4. 4 0. 6 4. 5 54 4. 2 7. 3

Sample Problems Vi (m/s) Vf (m/s) a (m/s^2) d (m) t(s) -4. 2 54 7. 3

What information does the shape of the curve provide? Negative Acceleration Position Decreasing Velocity Position Positive Acceleration Time Position Increasing Velocity Time

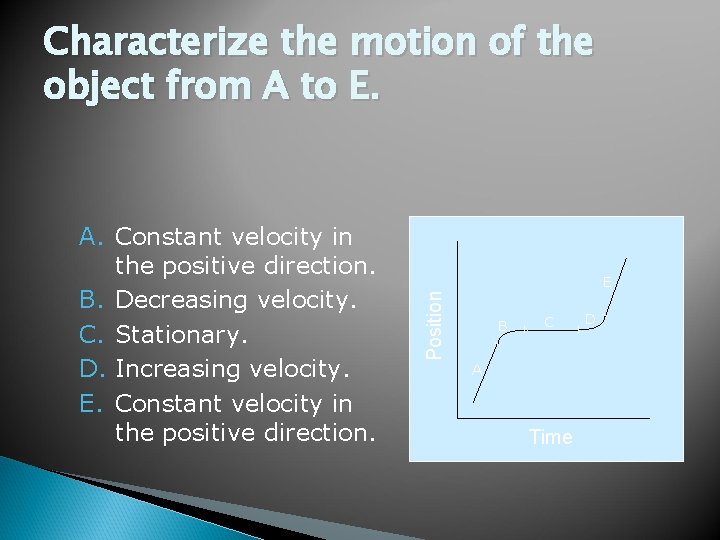
Characterize the motion of the object from A to E. E Position A. Constant velocity in the positive direction. B. Decreasing velocity. C. Stationary. D. Increasing velocity. E. Constant velocity in the positive direction. B C A Time D

What information does the slope of the curve provide? Positively sloped curve = movement in the positive direction. n Negatively sloped curve = movement in the negative direction. Position n Time Positive Direction Negative Direction

What else does the slope tell us? n What is the motion described by each curve? How does the velocity of each curve compare to one another? • • • A is stationary B is moving at the same speed as C, but their starting position is different. D is moving slower than B or C. C Position n B A D Time

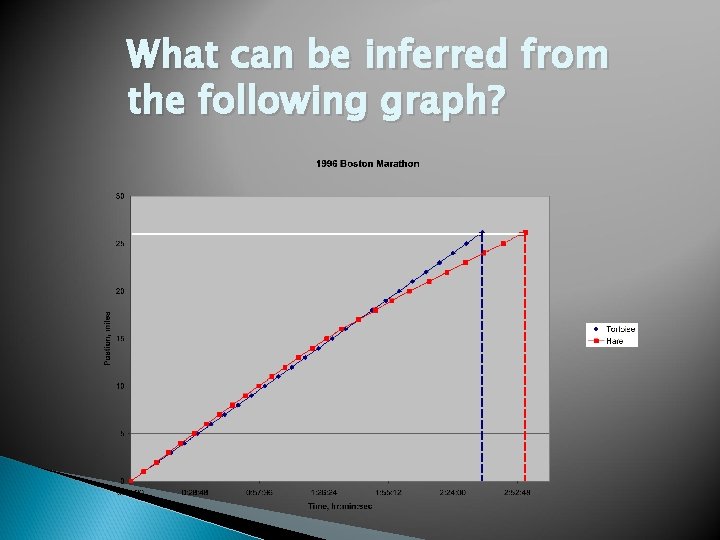
What can be inferred from the following graph?

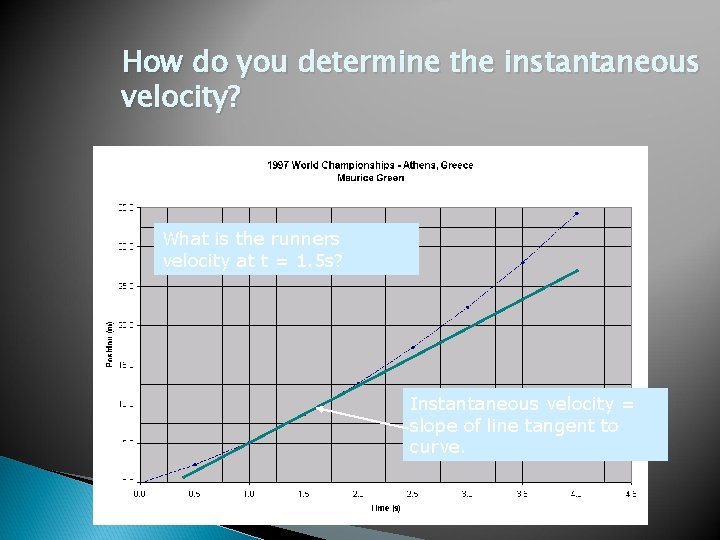
How do you determine the instantaneous velocity? What is the runners velocity at t = 1. 5 s? Instantaneous velocity = slope of line tangent to curve.

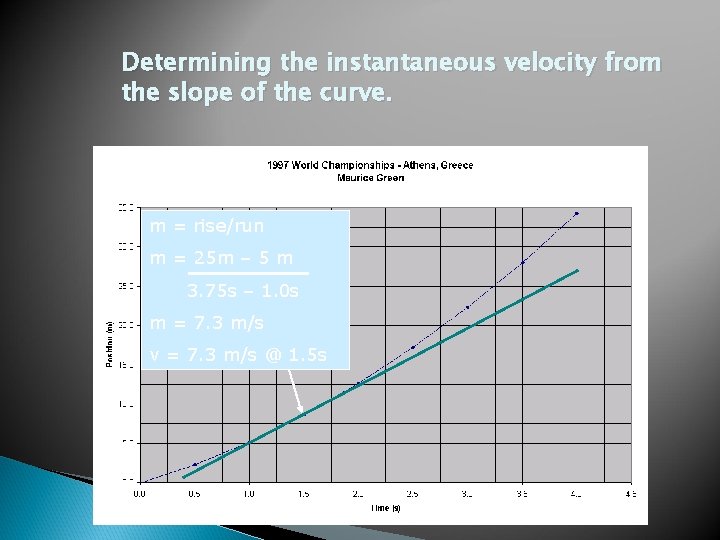
Determining the instantaneous velocity from the slope of the curve. m = rise/run m = 25 m – 5 m 3. 75 s – 1. 0 s m = 7. 3 m/s v = 7. 3 m/s @ 1. 5 s

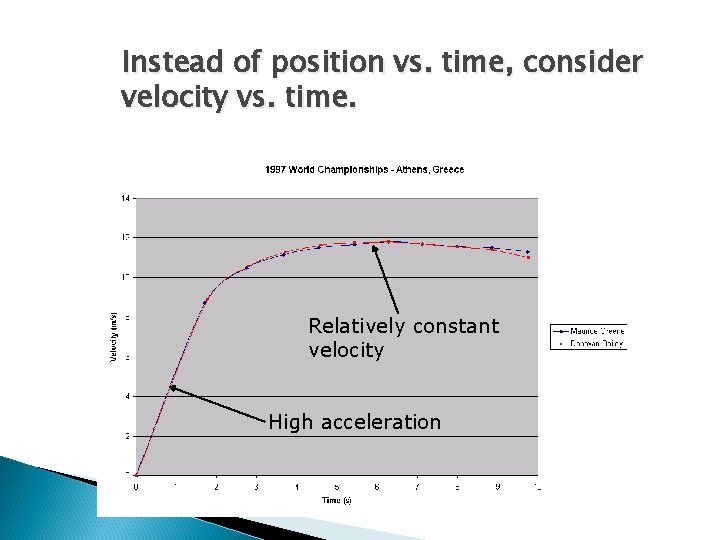
Instead of position vs. time, consider velocity vs. time. Relatively constant velocity High acceleration

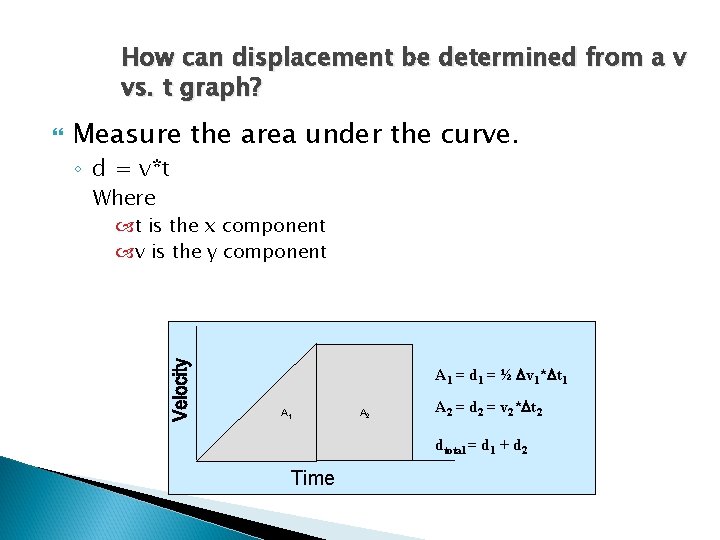
How can displacement be determined from a v vs. t graph? Measure the area under the curve. ◦ d = v*t Where t is the x component v is the y component A 1 = d 1 = ½ v 1* t 1 A 2 A 2 = d 2 = v 2* t 2 dtotal = d 1 + d 2 Time

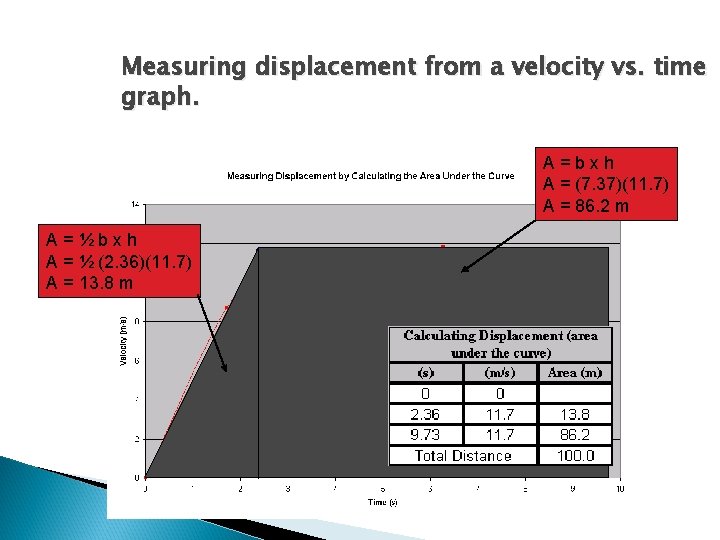
Measuring displacement from a velocity vs. time graph. A=bxh A = (7. 37)(11. 7) A = 86. 2 m A=½bxh A = ½ (2. 36)(11. 7) A = 13. 8 m

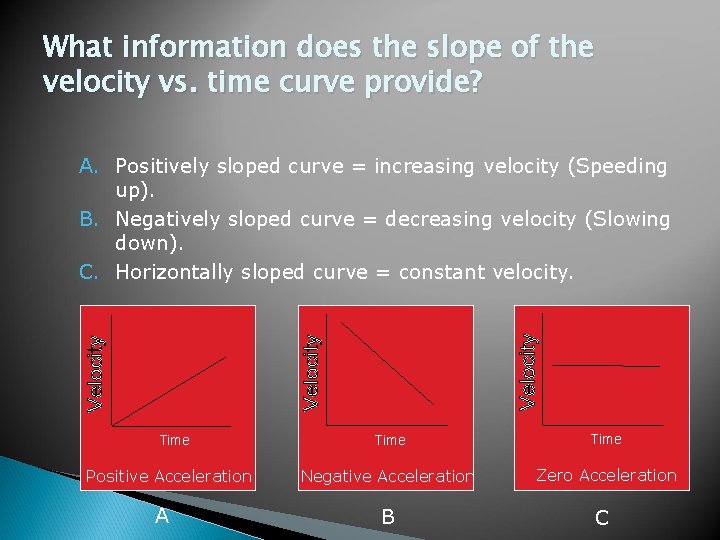
What information does the slope of the velocity vs. time curve provide? A. Positively sloped curve = increasing velocity (Speeding up). B. Negatively sloped curve = decreasing velocity (Slowing down). C. Horizontally sloped curve = constant velocity. Time Positive Acceleration A Time Negative Acceleration Zero Acceleration B C

Determining velocity from acceleration If acceleration is considered constant: a = v/ t = (vf – vi)/(tf – ti) ◦ Since ti is normally set to 0, this term can be eliminated. ◦ Rearranging terms to solve for vf results in: vf = vi + at Time Positive Acceleration

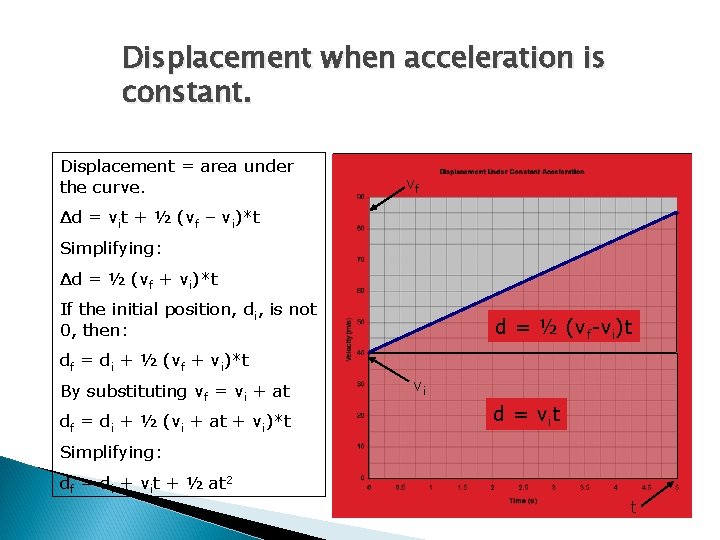
Displacement when acceleration is constant. Displacement = area under the curve. vf Δd = vit + ½ (vf – vi)*t Simplifying: Δd = ½ (vf + vi)*t If the initial position, di, is not 0, then: d = ½ (vf-vi)t df = di + ½ (vf + vi)*t By substituting vf = vi + at df = di + ½ (vi + at + vi)*t vi d = v it Simplifying: df = di + vit + ½ at 2 t