Acceleration Changes in Velocity Changes in velocity include

Acceleration

Changes in Velocity • Changes in velocity include: – Speeding up – Slowing down – Any change in direction • Any change in velocity is called an Acceleration!

Acceleration • The acceleration of an object is its change in velocity over a certain period of time. • We calculate acceleration by the following equation: Ø Acceleration (a) = final velocity – initial velocity Ø a = Dv t time

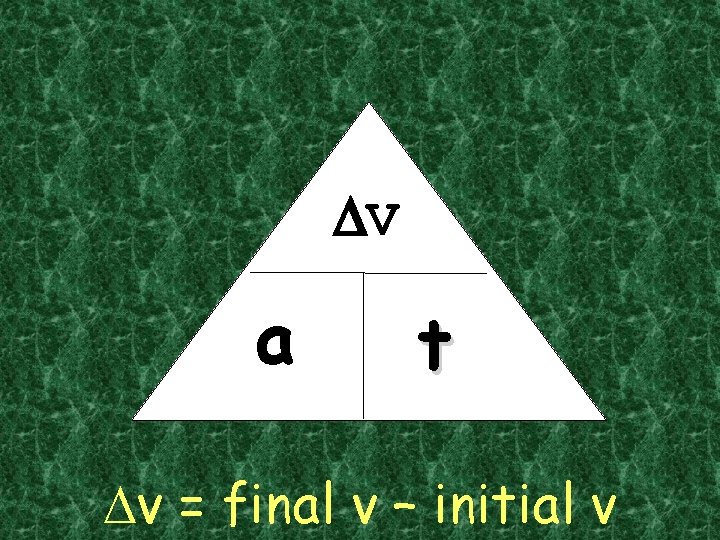
DV a t Dv = final v – initial v

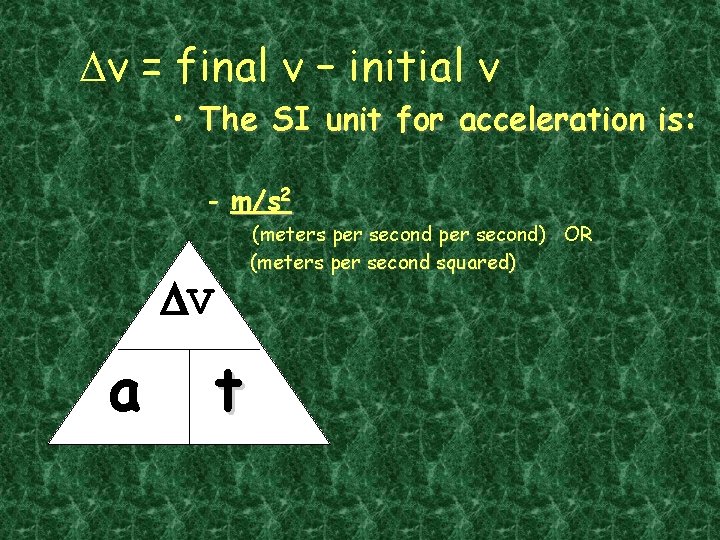
Dv = final v – initial v • The SI unit for acceleration is: - m/s 2 (meters per second) OR (meters per second squared) DV a t

Acceleration Values • Acceleration is a vector, so it has a magnitude and a direction. • Acceleration values may be positive or negative. • To tell if you’re speeding up or slowing down, match up the direction of the velocity with the direction of the acceleration.

Acceleration Values Slowing Down Speeding Up • Velocity and acceleration are the same direction. (Both + or both -) + + • Velocity and acceleration are in opposite directions. (One +, one -) v + a - v a

Acceleration Values cont. • A small acceleration value means that speed is increasing or decreasing slowly. • A large acceleration value means that speed is increasing or decreasing rapidly. • An object at constant velocity has no (zero) acceleration – it is not speeding up, slowing down or changing direction!

Let’s Practice! Practice Problem … A flowerpot falls off a second-story windowsill. The flowerpot starts from rest and hits the sidewalk 1. 5 s later with a velocity of 14. 7 m/s. Find the average acceleration of the flowerpot.

• List the given and unknown values. – Given: time, t = 1. 5 s initial velocity, initial v = 0 m/s down final velocity, final v = 14. 7 m/s down – Unknown: acceleration, a = ? m/s 2 down • Write the equation for acceleration. Ø Acceleration (a) = final velocity – initial velocity time Ø a = Dv t

• Insert the known values and solve. Øa = Dv = (final v – initial v) = t t = (14. 7 m/s – 0 m/s) 1. 5 s Ø a = 14. 7 m/s = 9. 8 m/s 2 down 1. 5 s

Now you get to practice!

1. ) A turtle swimming in a straight line toward the shore has a speed of 0. 50 m/s. After 4. 0 s, its speed is 0. 80 m/s. What is the turtle’s average acceleration? 2. ) Find the average acceleration of a northbound subway train that slows down from 12 m/s to 9. 6 m/s in 0. 8 s. 3. ) Marissa’s car accelerates at an average rate of 2. 6 m/s 2. Calculate how long it takes her car to accelerate from 24. 6 m/s to 26. 8 m/s.

1) Natalie accelerates her skateboard along a straight path from 0 m/s to 4. 0 m/s in 2. 5 s. Find her average acceleration. Ø 1. 6 m/s 2 along her path 2) A turtle swimming in a straight line toward the shore has a speed of 0. 50 m/s. After 4. 0 s, its speed is 0. 80 m/s. What is the turtle’s average acceleration? Ø. 075 m/s 2 toward the shore

3) Find the average acceleration of a northbound subway train that slows down from 12 m/s to 9. 6 m/s in 0. 8 s. Ø -3 m/s 2 north 4) Marissa’s car accelerates at an average rate of 2. 6 m/s 2. Calculate how long it takes her car to accelerate from 24. 6 m/s to 26. 8 m/s. Ø 0. 85 s

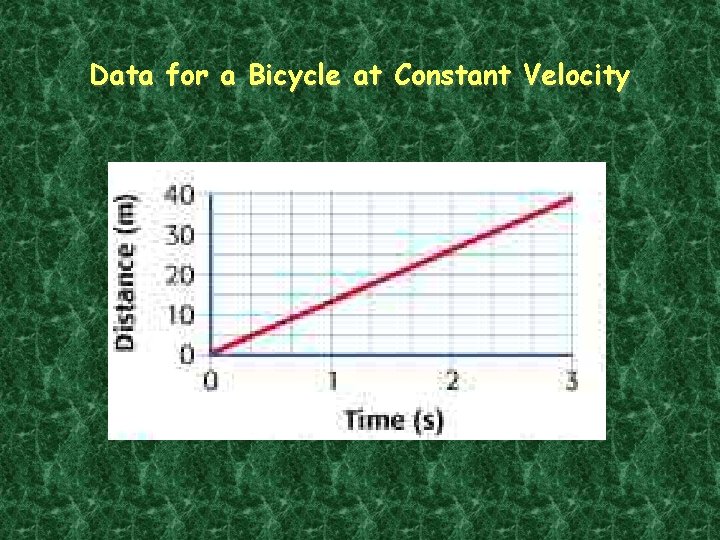
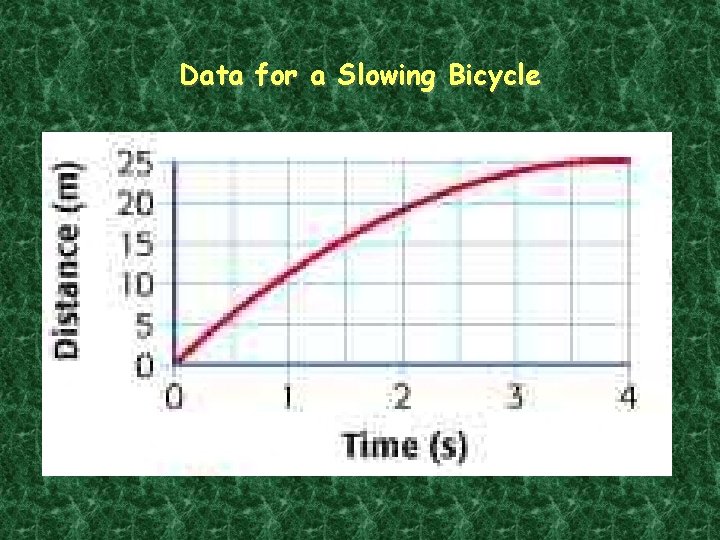
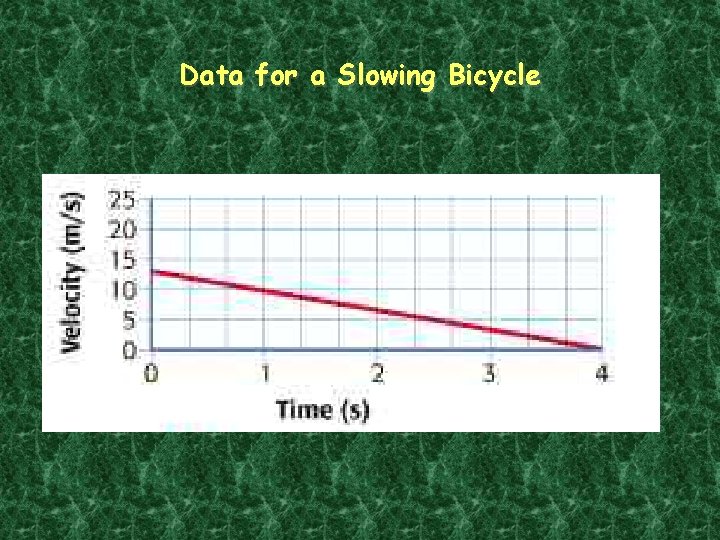
Motion Graphs When the motion of an object is graphed by plotting the distance it travels versus time, the slope of the resulting line is the object’s speed.

Data for a Bicycle at Constant Velocity

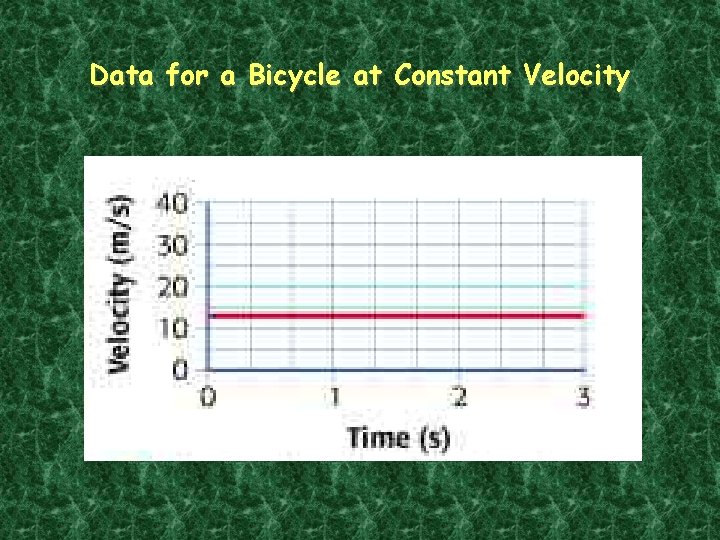
Data for a Bicycle at Constant Velocity

Data for a Slowing Bicycle

Data for a Slowing Bicycle

Homework … • Acceleration Worksheet