Accelerating Gibbs sampling of Gaussians using matrix decompositions

Accelerating Gibbs sampling of Gaussians using matrix decompositions Al Parker January 18, 2009

Acknowledgements • Colin Fox, Physics, University of Otago • New Zealand Institute of Mathematics, University of Auckland • Center for Biofilm Engineering, , Bozeman

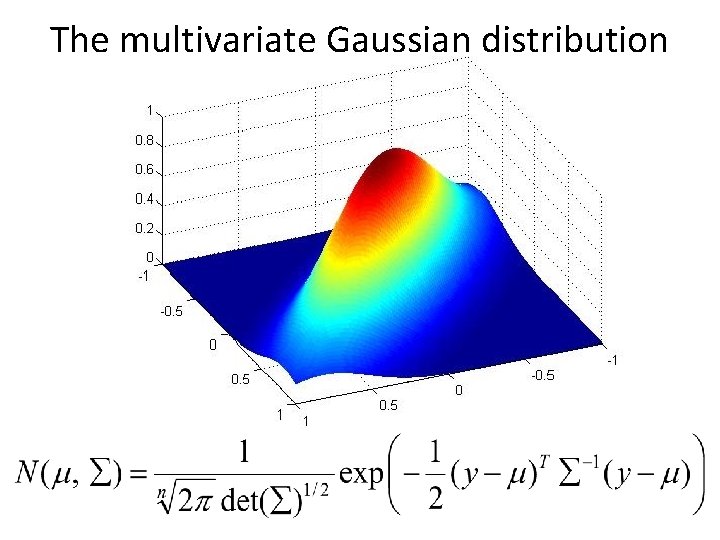
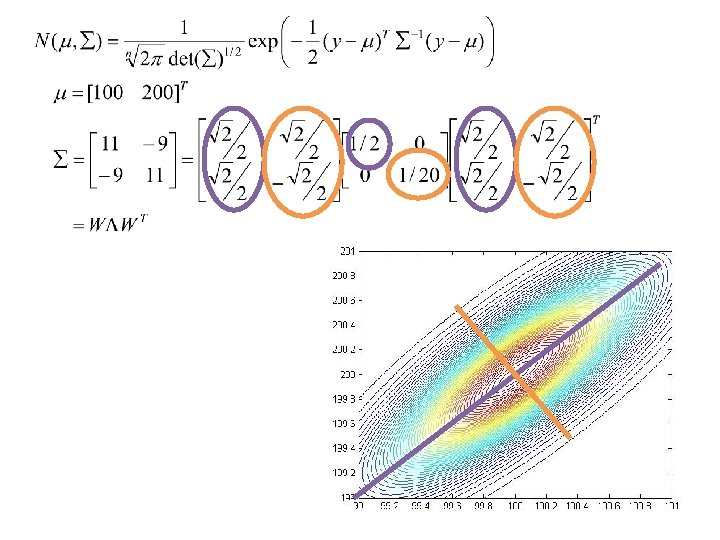
The multivariate Gaussian distribution

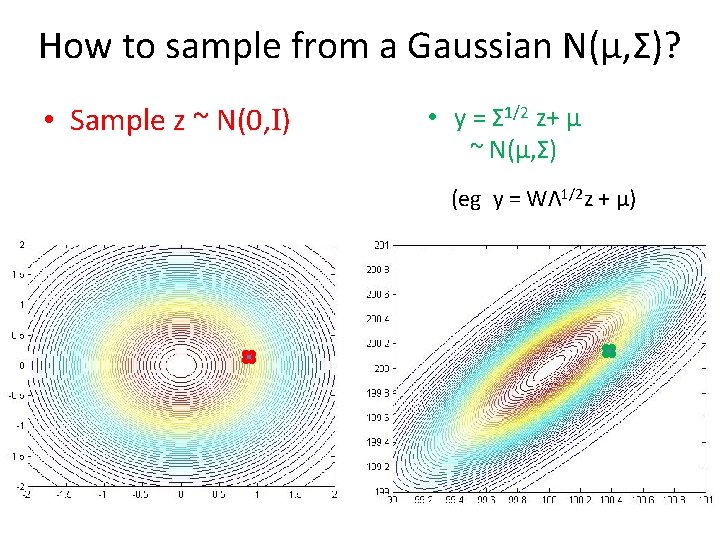
How to sample from a Gaussian N(µ, Σ)? • Sample z ~ N(0, I) • y = Σ 1/2 z+ µ ~ N(µ, Σ) (eg y = WΛ 1/2 z + µ)

Example: From 64 faces, modeling “face space” with a Gaussian Process N(μ, Σ) Pixel intensity at the ith row and jth column is y(s(i, j)), y(s) є R 112 x R 112 μ(s) є R 112 x R 112 Σ(s, s) є R 12544 x R 12544

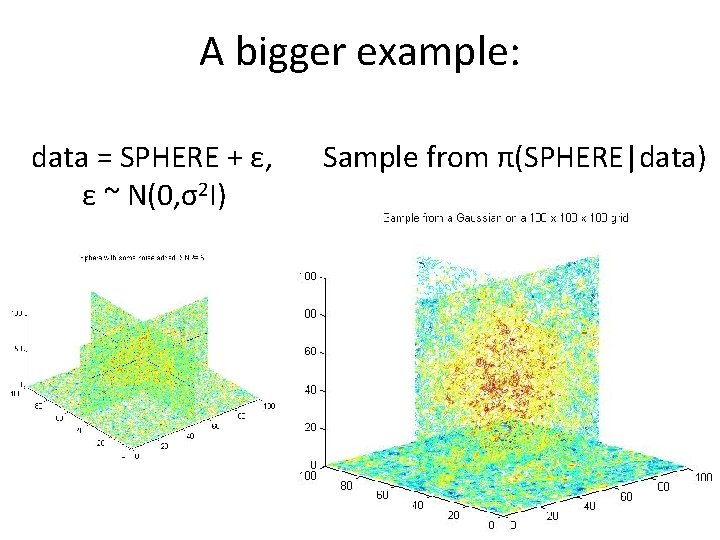
A bigger example: data = SPHERE + ε, ε ~ N(0, σ2 I) Sample from π(SPHERE|data)

The problem • To generate a sample y = Σ 1/2 z+ µ ~ N(µ, Σ), how to calculate the factorization Σ =Σ 1/2(Σ 1/2)T ? • Σ 1/2 = WΛ 1/2 by eigen-decomposition, 10/3 n 3 flops • Σ 1/2 = C by Cholesky factorization, 1/3 n 3 flops LARGE For Gaussians (n>105, eg in image analysis and global data sets), these approaches are not possible • n 3 is computationally TOO EXPENSIVE • storing an n x n matrix requires TOO MUCH MEMORY

Some solutions Work with sparse precision matrix Σ-1 models (Rue, 2001) Circulant embeddings (Gneiting et al, 2005) Iterative methods: • Advantages: – COST: n 2 flops per iteration – MEMORY: Only vectors of size n x 1 need be stored • Disadvantages: – If the method runs for n iterations, then there is no cost savings over a direct method

Gibbs: an iterative sampler of N(0, A) and N(0, A-1 ) Let A=Σ or A= Σ-1 1. Split A into D=diag(A), L=lower(A), LT=upper(A) 2. Sample z ~ N(0, I) 3. Take conditional samples in each coordinate direction, so that a full sweep of all n coordinates is yk =-D-1 L yk - D-1 LT yk-1 + D-1/2 z yk converges in distribution geometrically to N(0, A-1) Ayk converges in distribution geometrically to N(0, A)

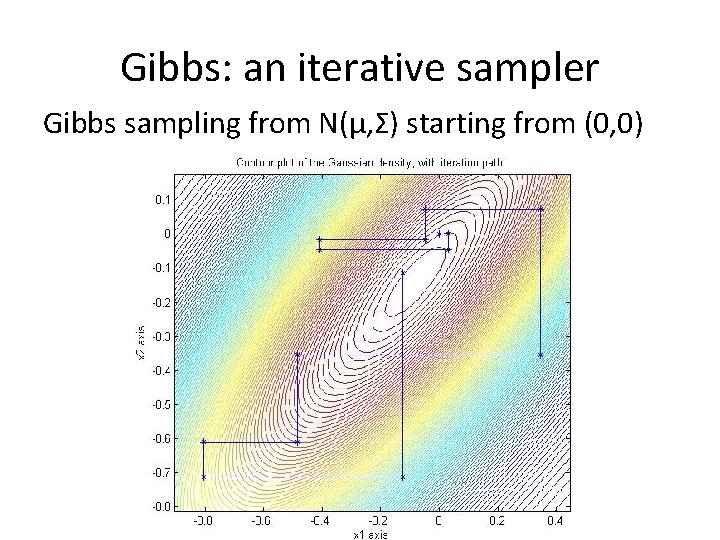
Gibbs: an iterative sampler Gibbs sampling from N(µ, Σ) starting from (0, 0)

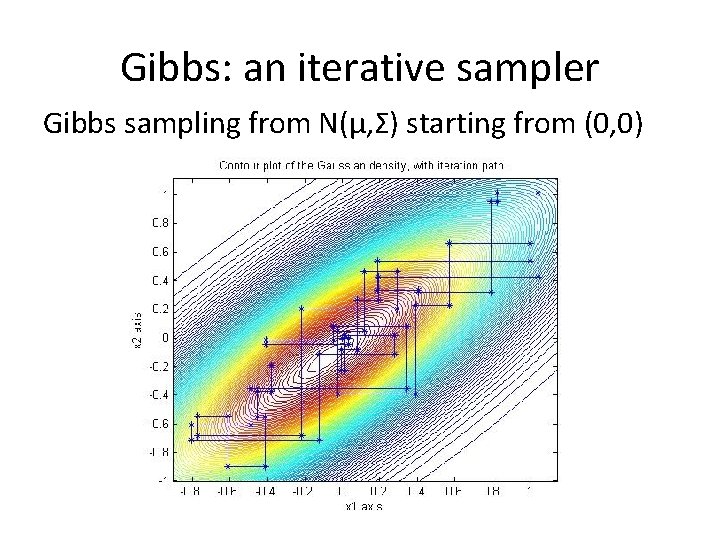
Gibbs: an iterative sampler Gibbs sampling from N(µ, Σ) starting from (0, 0)

What’s the link to Ax=b? Solving Ax=b is equivalent to minimizing an ndimensional quadratic (when A is spd) A Gaussian is sufficiently specified by the same quadratic (with A= Σ-1 and b=Aμ):

Gauss-Siedel Linear Solve of Ax=b 1. Split A into D=diag(A), L=lower (A), LT=upper(A) 2. Minimize the quadratic f(x) in each coordinate direction, so that a full sweep of all n coordinates is xk =-D-1 L xk - D-1 LT xk-1 + D-1 b xk converges geometrically A-1 b

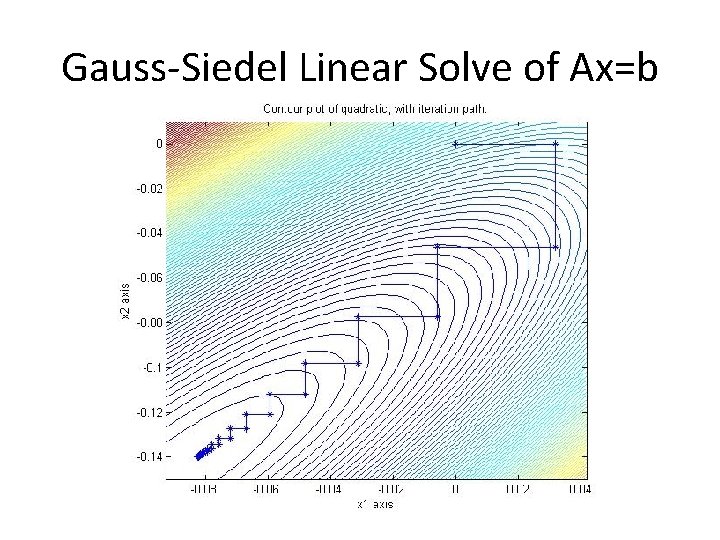
Gauss-Siedel Linear Solve of Ax=b

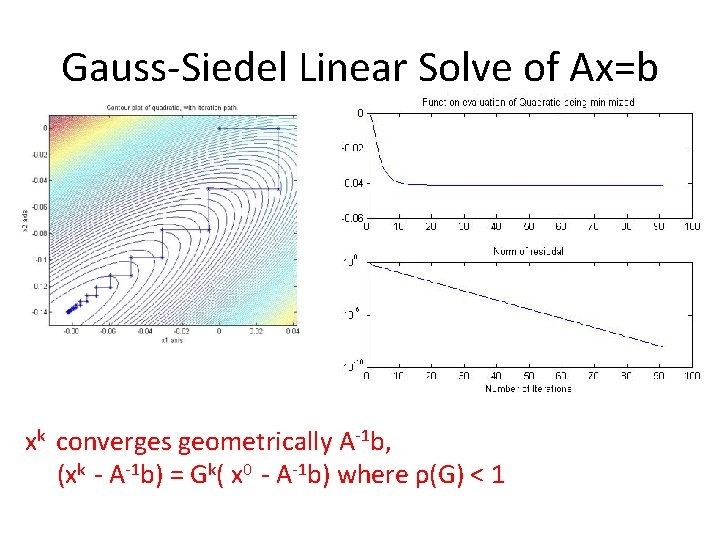
Gauss-Siedel Linear Solve of Ax=b xk converges geometrically A-1 b, (xk - A-1 b) = Gk( x 0 - A-1 b) where ρ(G) < 1

Theorem: A Gibbs sampler is a Gauss Siedel linear solver Proof: • A Gibbs sampler is yk =-D-1 L yk - D-1 LT yk-1 + D-1/2 z • A Gauss-Siedel linear solve of Ax=b is xk =-D-1 L xk - D-1 LT xk-1 + D-1 b

Gauss Siedel is a Stationary Linear Solver • A Gauss-Siedel linear solve of Ax=b is xk =-D-1 L xk - D-1 LT xk-1 + D-1 b • Gauss Siedel can be written as M xk = N xk-1 + b where M = D + L and N = D - LT , A = M – N, the general form of a stationary linear solver

Stationary linear solvers of Ax=b 1. Split A=M-N 2. Iterate Mxk = N xk-1 + b 1. Split A=M-N 2. Iterate xk = M-1 Nxk-1 + M-1 b = Gxk-1 + M-1 b xk converges geometrically A-1 b, (xk - A-1 b) = Gk( x 0 - A-1 b) when ρ(G) = ρ(M-1 N)< 1

Stationary Samplers from Stationary Solvers Solving Ax=b: 1. Split A=M-N 2. Iterate Mxk = N xk-1 + b xk A-1 b if ρ(M-1 N)< 1 Sampling from N(0, A) and N(0, A-1): 1. Split A=M-N 2. Iterate Myk = N yk-1 + ck-1 where ck-1 ~ N(0, MT + N) yk N(0, A-1) if ρ(M-1 N)< 1 Ayk N(0, A) if ρ(M-1 N)< 1

How to sample ck-1 ~ N(0, MT + N) ? • Gauss Siedel M = D + L, ck-1 ~ N(0, D) • SOR (successive over-relaxation) M = 1/w. D + L, ck-1 ~ N(0, (2 -w)/w D) • Richardson M = I, ck-1 ~ N(0, 2 I-A) • Jacobi M = D, ck-1 ~ N(0, 2 D-A)

Theorem: Stat Linear Solver converges iff Stat Sampler converges and the convergence is geometric • Proof: They have the same iteration operator: For linear solves: xk = Gxk-1 + M-1 b so that (xk - A-1 b) = Gk( x 0 - A-1 b) For sampling: yk = Gyk-1 + M-1 ck-1 E(yk)= Gk E(y 0) Var(yk) = A-1 - Gk A-1 Gk. T Proof for Gaussians given by Barone and Frigessi, 1990. For arbitrary distributions by Duflo, 1997

Acceleration schemes for stationary linear solvers can be used to accelerate stationary samplers Polynomial acceleration of a stationary solver of Ax=b is 1. Split A = M - N 2. xk+1 = (1 - vk) xk-1 + vk xk + vk uk M-1 (b-A xk) which replaces (xk - A-1 b) = Gk( x 0 - A-1 b) with a kth order polynomial (xk - A-1 b) = p(G)( x 0 - A-1 b)

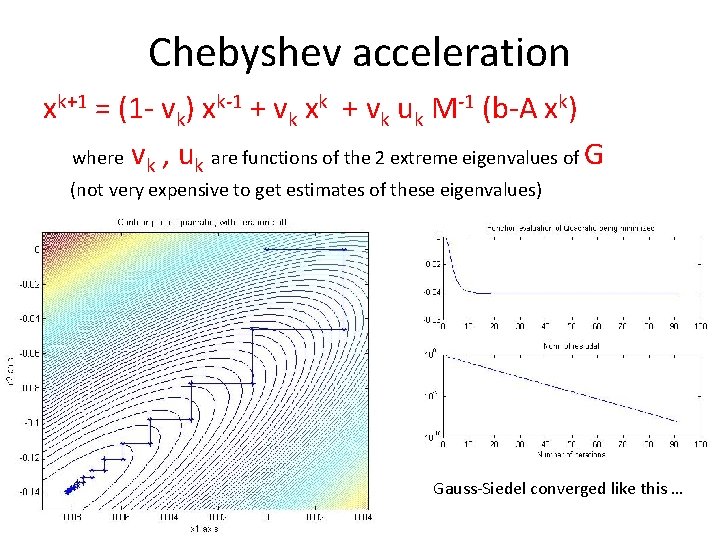
Chebyshev acceleration xk+1 = (1 - vk) xk-1 + vk xk + vk uk M-1 (b-A xk) where vk , uk are functions of the 2 extreme eigenvalues of G (not very expensive to get estimates of these eigenvalues) Gauss-Siedel converged like this …

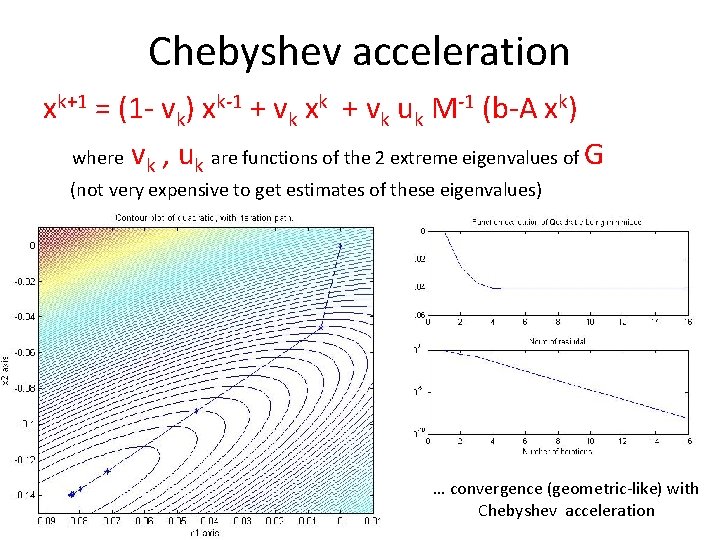
Chebyshev acceleration xk+1 = (1 - vk) xk-1 + vk xk + vk uk M-1 (b-A xk) where vk , uk are functions of the 2 extreme eigenvalues of G (not very expensive to get estimates of these eigenvalues) … convergence (geometric-like) with Chebyshev acceleration

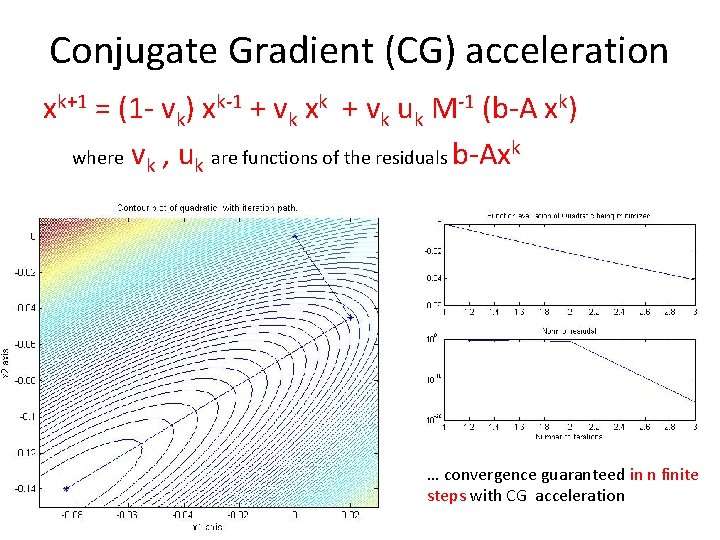
Conjugate Gradient (CG) acceleration xk+1 = (1 - vk) xk-1 + vk xk + vk uk M-1 (b-A xk) where vk , uk are functions of the residuals b-Axk … convergence guaranteed in n finite steps with CG acceleration

Polynomial accelerated sampler of N(0, A-1) if vk , uk are independent of the iterates yk , ck 1. Split A = M - N 2. yk+1 = (1 - vk) yk-1 + vk yk + vk uk M-1 (ck -A yk) where ck ~ N(0, (2 -vk)/vk ( (2 – uk)/ uk M + N)

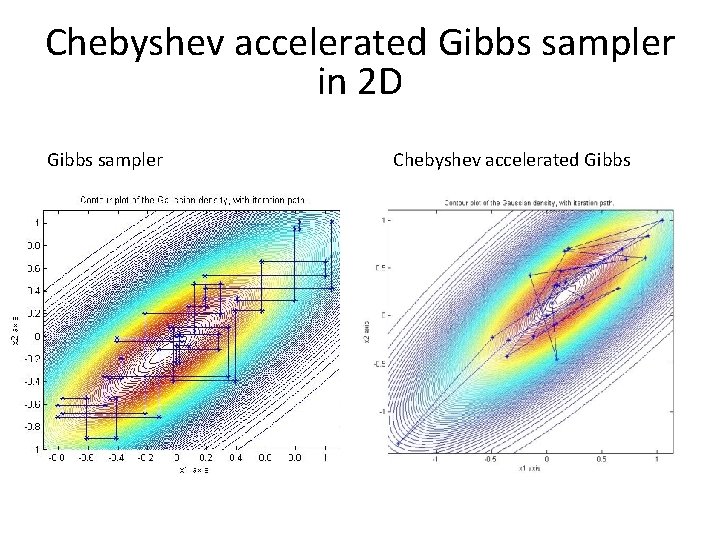
Chebyshev accelerated Gibbs sampler in 2 D Gibbs sampler Chebyshev accelerated Gibbs

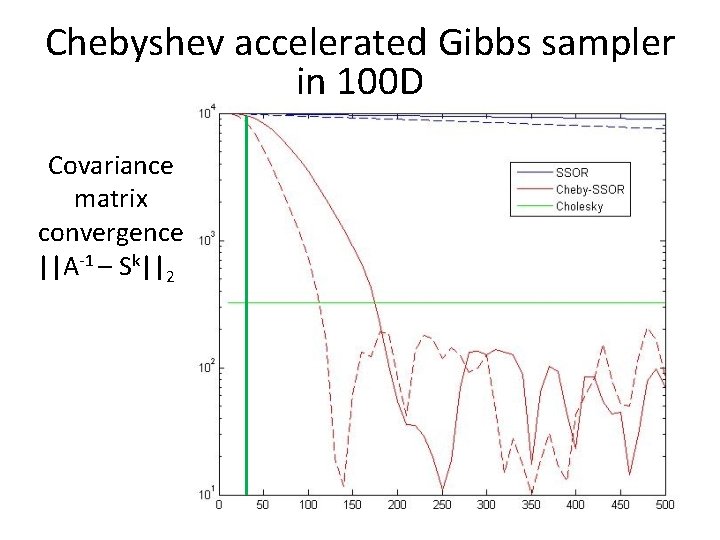
Chebyshev accelerated Gibbs sampler in 100 D Covariance matrix convergence ||A-1 – Sk||2

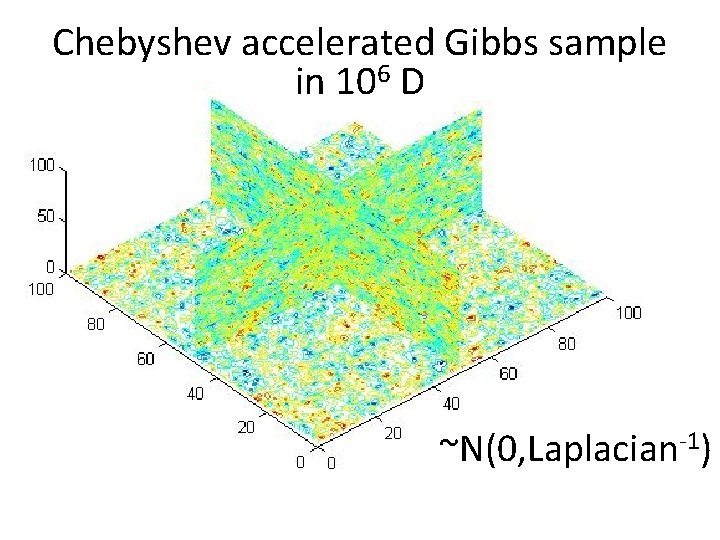
Chebyshev accelerated Gibbs sample in 106 D ~N(0, Laplacian-1)

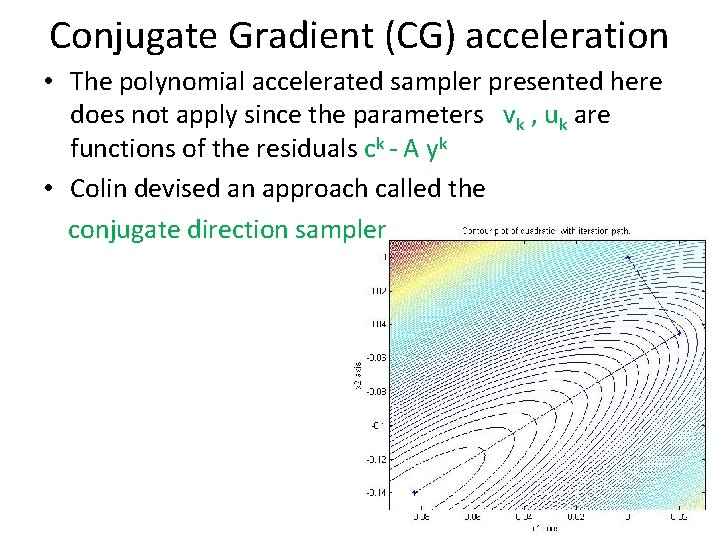
Conjugate Gradient (CG) acceleration • The polynomial accelerated sampler presented here does not apply since the parameters vk , uk are functions of the residuals ck - A yk • Colin devised an approach called the conjugate direction sampler

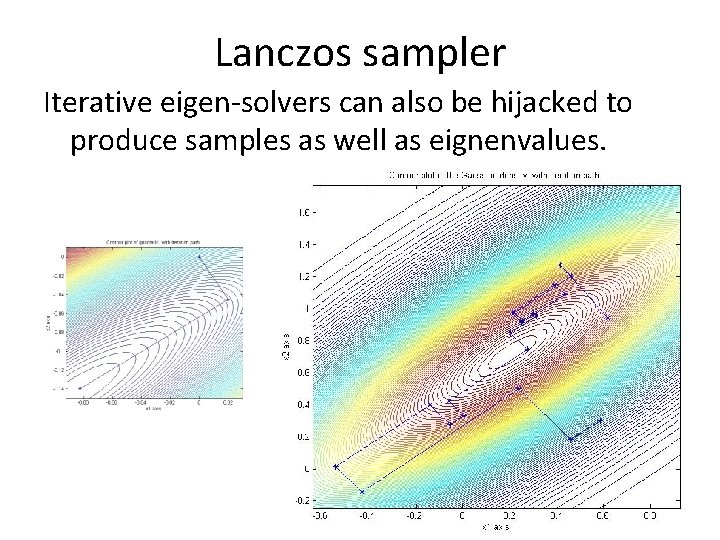
Lanczos sampler Iterative eigen-solvers can also be hijacked to produce samples as well as eignenvalues.

One extremely effective sampler for LARGE Gaussians Use a combination of the ideas presented: • Use the Lanczos or CD sampler to generate samples and estimates of the extreme eigenvalues of G. • Seed these samples and extreme eigenvalues into a Chebyshev accelerated SOR sampler

Conclusions Common techniques from numerical linear algebra can be used to sample from Gaussians • Cholesky factorization (precise but expensive) • Any stationary linear solver can be used as a stationary sampler (inexpensive but with geometric convergence) • Polynomial accelerated Samplers – Chebyshev – Conjugate Gradients • Lanczos Sampler

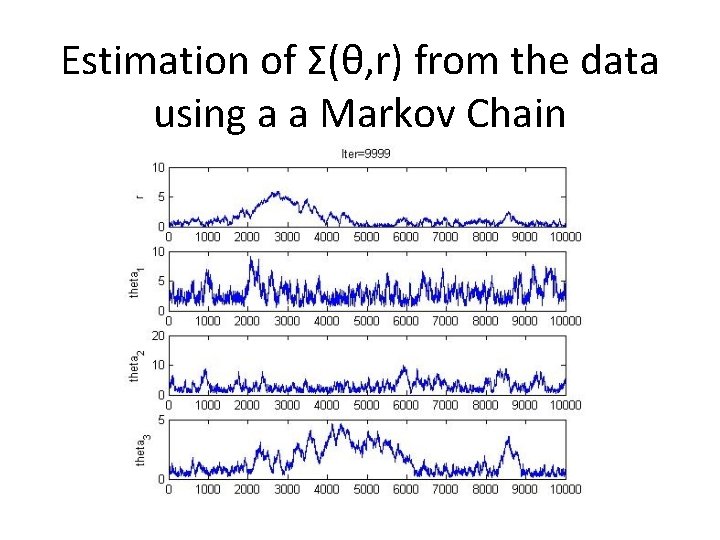
Estimation of Σ(θ, r) from the data using a a Markov Chain

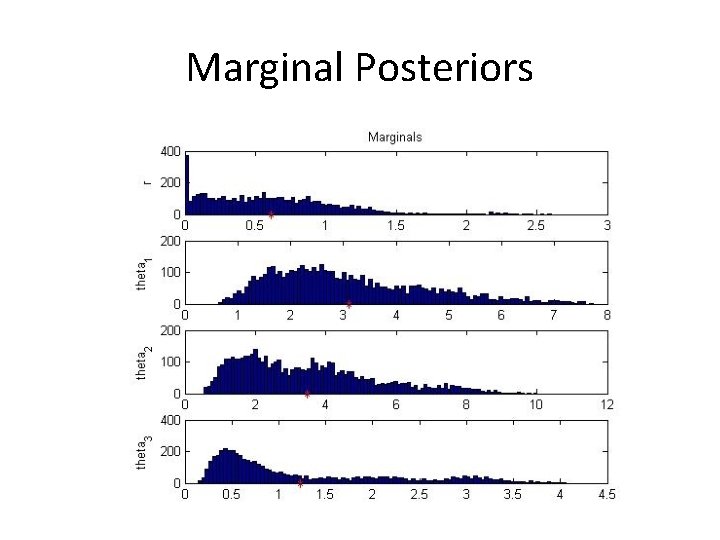
Marginal Posteriors

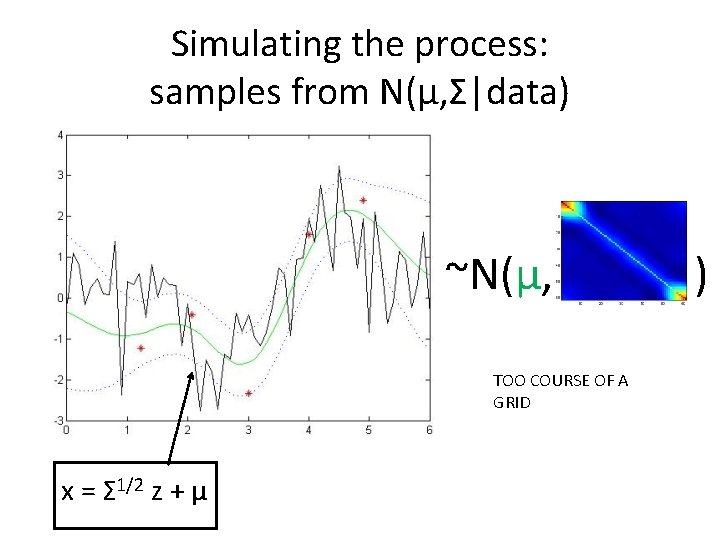
Simulating the process: samples from N(μ, Σ|data) ~N(μ, TOO COURSE OF A GRID x = Σ 1/2 z + µ )

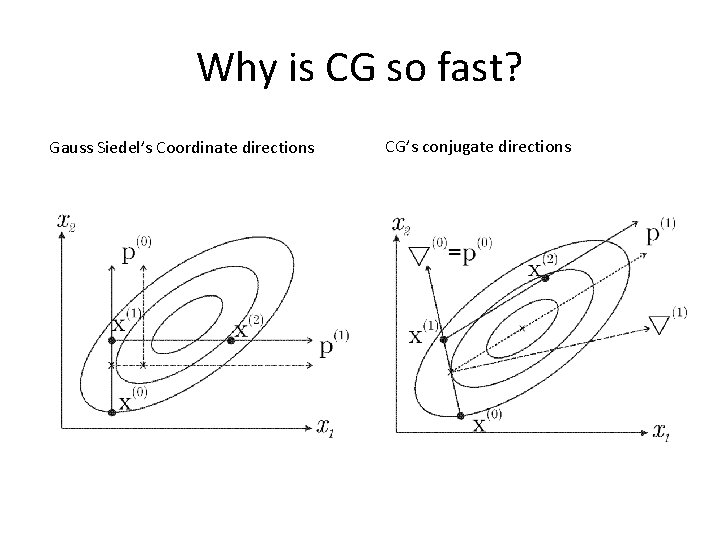
Why is CG so fast? Gauss Siedel’s Coordinate directions CG’s conjugate directions

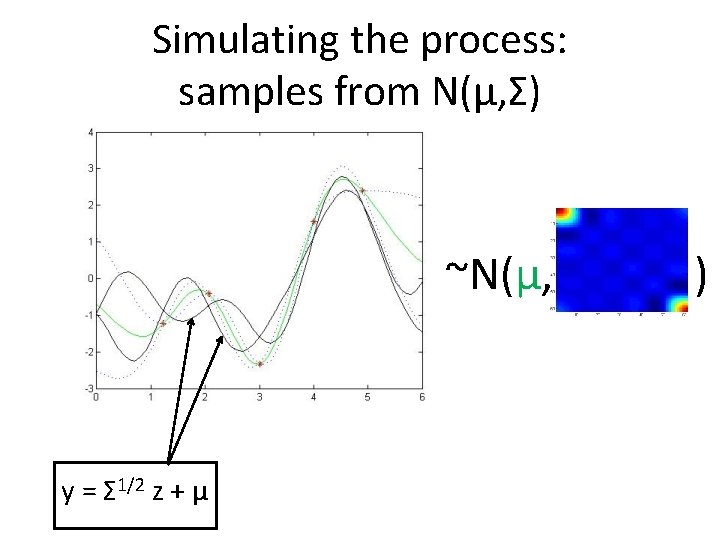
Simulating the process: samples from N(μ, Σ) ~N(μ, y = Σ 1/2 z + µ )

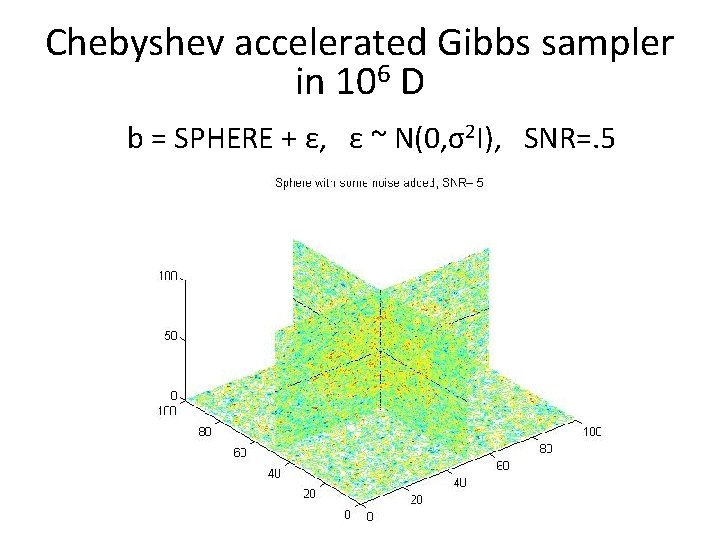
Chebyshev accelerated Gibbs sampler in 106 D b = SPHERE + ε, ε ~ N(0, σ2 I), SNR=. 5

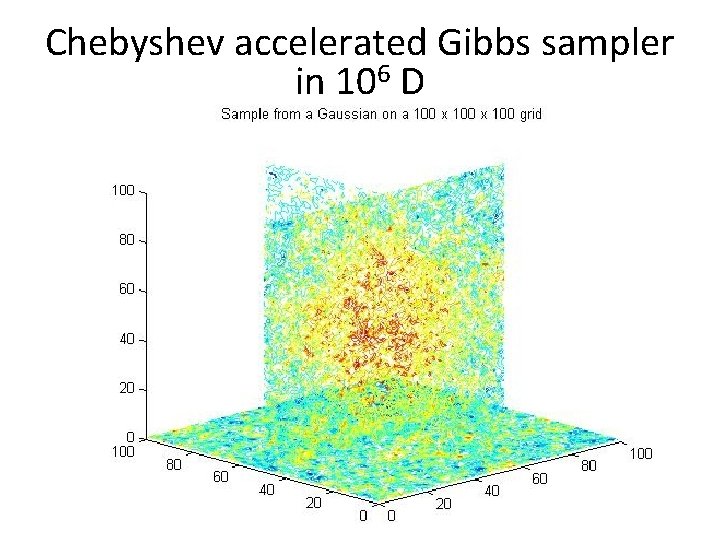
Chebyshev accelerated Gibbs sampler in 106 D

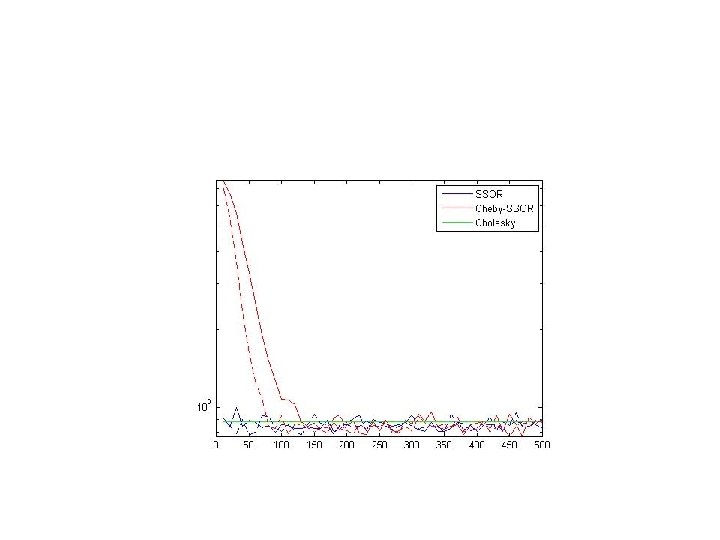
CD sampler (CG accelerated Gibbs) • A GOOD THING: The CG algorithm is a great linear solver! If the eigenvalues of A are in c clusters, then a solution to Ax=b is found in c << n steps. • A PROBLEM: When the CG residuals get small , the CD sampler is forced to stop after only c << n steps. Thus, covariances with well separated eigenvalues work well. • The covariance of the CD samples yk ~ N(0, A-1) and Ayk ~ N(0, A) have the correct covariances if A’s eigenvectors in the Krylov space spanned by the residuals have small/large eigenvalues.

Another example: Interpolation

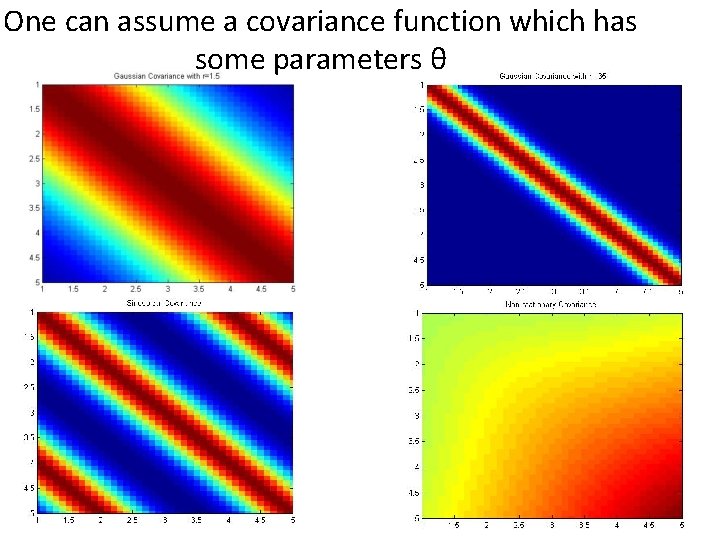
One can assume a covariance function which has some parameters θ

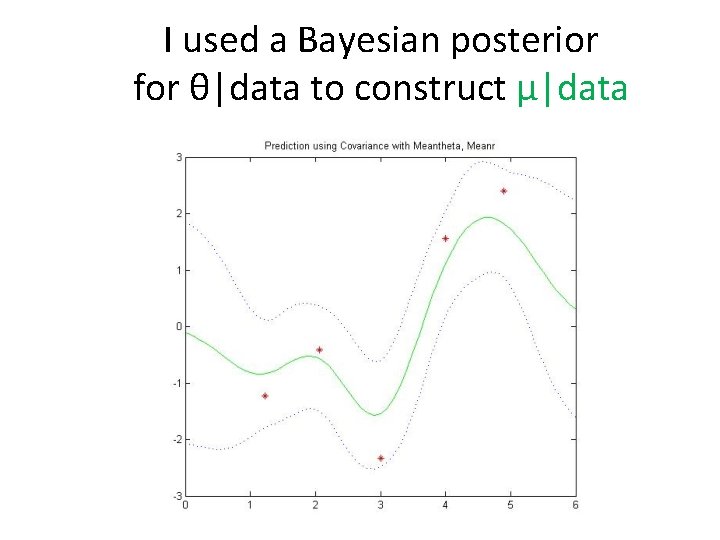
I used a Bayesian posterior for θ|data to construct μ|data

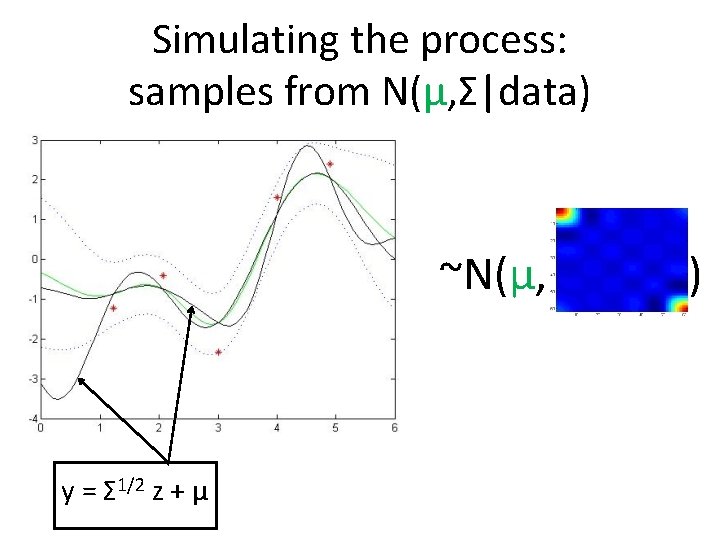
Simulating the process: samples from N(μ, Σ|data) ~N(μ, y = Σ 1/2 z + µ )

Gaussian Processes modeling global ozone Cressie and Johannesson, Fixed rank kriging for very large spatial datasets, 2006

Gaussian Processes modeling global ozone

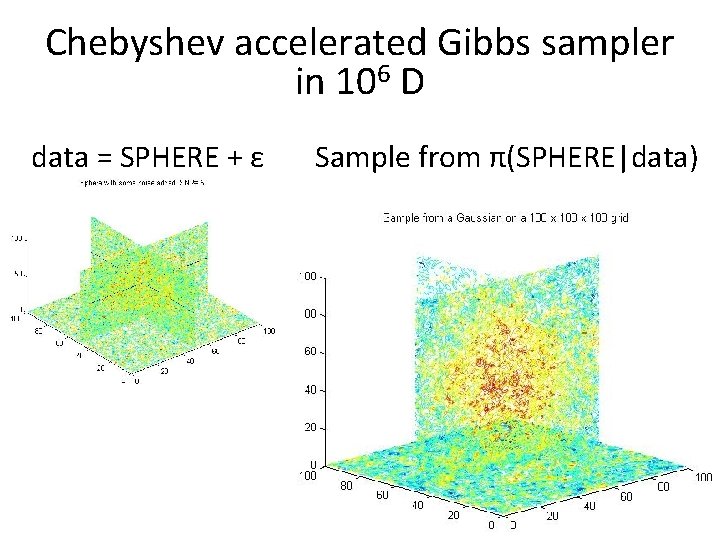
Chebyshev accelerated Gibbs sampler in 106 D data = SPHERE + ε Sample from π(SPHERE|data)