Accelerating Change in Your Organization Using Six Sigma

Accelerating Change in Your Organization Using Six Sigma Prepared for CQAA February 19, 2004 by Dr. Nancy Eickelmann Team Contributors: Dr. Jongmoon Baik, Animesh Anant Software and System Engineering Research Laboratory MOTOROLA LABS 1

Outline • • Change Acceleration with Six Sigma How do we use DMAIC for change? How do we control variation? Conclusion 2

What is Six Sigma? “Six Sigma is a 4 -step high performance system to execute business strategy. ” Matt Barney, Motorola Inc. 1. 2. 3. 4. Align executives to the right objectives and targets Mobilize improvement teams Accelerate results Govern sustained improvement http: //www. asq. org/pub/sixsigma/motorolafigs. html 3

Accelerating Change - What • Create a Community of Practice • Create a Community of Practicioners, i. e. , – MBB, GB • Foster a Quality Culture that Institutionalizes Best Practices and Change for Improvement • Maintain Strategic Focus 4

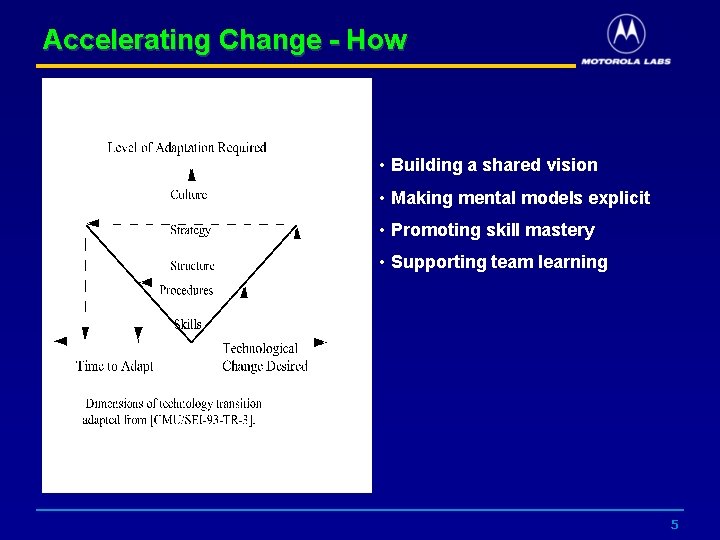
Accelerating Change - How • Building a shared vision • Making mental models explicit • Promoting skill mastery • Supporting team learning 5

How Do We Use DMAIC for Change? 6

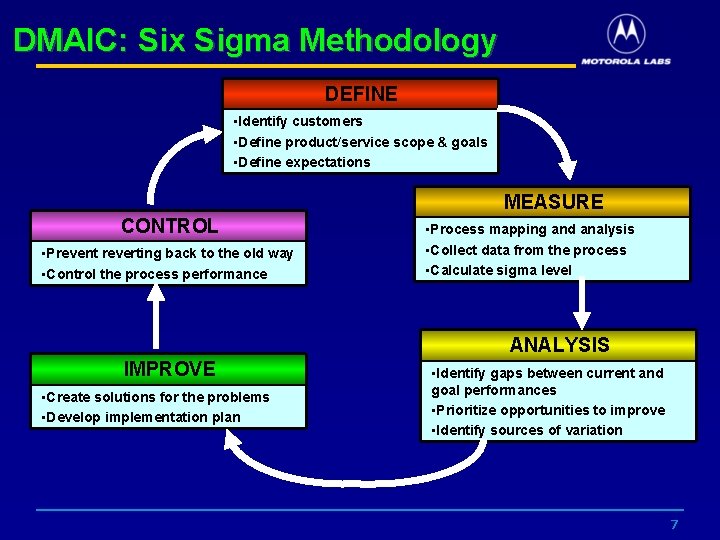
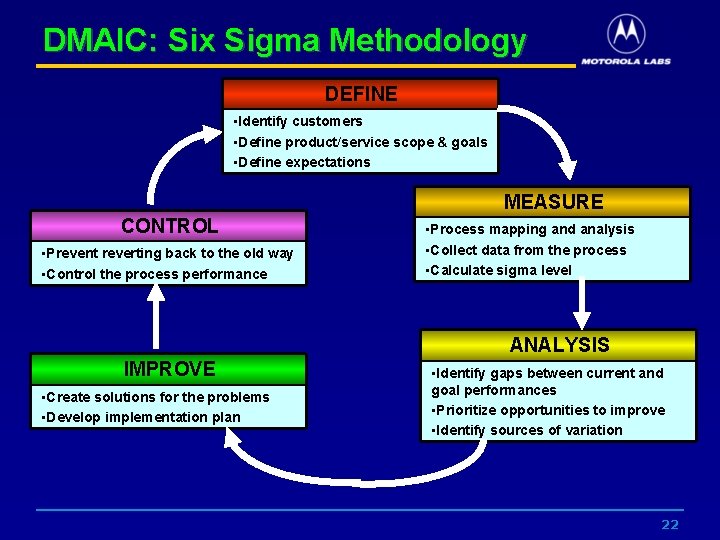
DMAIC: Six Sigma Methodology DEFINE • Identify customers • Define product/service scope & goals • Define expectations MEASURE CONTROL • Prevent reverting back to the old way • Control the process performance • Process mapping and analysis • Collect data from the process • Calculate sigma level ANALYSIS IMPROVE • Create solutions for the problems • Develop implementation plan • Identify gaps between current and goal performances • Prioritize opportunities to improve • Identify sources of variation 7

Project Charter Project Name Project Information • Leader • Master Black Belt • Project Start • Project End • Cost of Poor Quality Team Members • Executive Sponsor • Black Belt • Master Black Belt • Subject Matter Experts Process Start/Stop • Start Point • Stop Point Project Time-Frame • Milestone(s) • Date(s) Process Importance 1. … n. Process Problem 1. … n. Project Goals 1. … n. Process Measurements 1. … n. 2001 i. Six. Sigma. LLC http: //www. i. Six. Sigma. com 8

Applying DOE 1. 2. 3. 4. 5. 6. 7. 8. State the Problem with Clarity Select the Output or Response Variables Identify the Process Variables Select the Factor Levels and Ranges of Factor Settings Select the Appropriate Experimental Design Plan the Experiment Execute the Experiment Analyze and Interpret the Results 9

Step 1: State the Problem with Clarity Defect Prevention is the most cost-effective means of producing high quality software. Fagan Inspections (FIs) have been shown to be an effective technique of defect prevention. Motorola has modified this process and performs Modified Fagan Inspections (MFIs) and Formal Technical Reviews (FTRs) Does it make a difference whether we use: 1. Fagan Inspections 2. Modified Fagan Inspections 3. Formal Technical Reviews 10

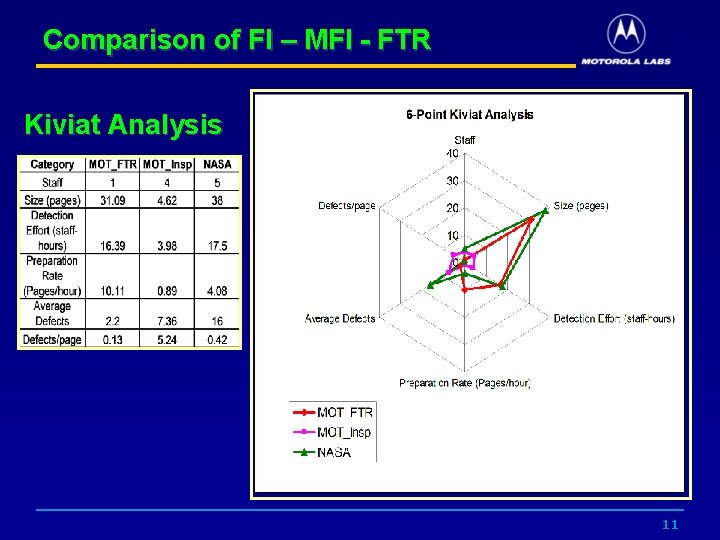
Comparison of FI – MFI - FTR Kiviat Analysis 11

Comparison of MFI - FTR Summary of measures • Number of Staff per Inspection/FTR • Staff effort expended in preparation and meeting time • Preparation Rate per Page • Preparation Rate per LOC • Average Defects Found • Defects per KSLOC ** The p-value (Prob > F) for every measure is statistically significant. The means for Inspections versus FTRs are significantly different for every measure. 12

Step 2: Select the Output or Response Variables • The output variables selected were: – staff hours of effort per Inspection/FTR – staff hours of effort per sub-activity – defects found per Inspection/FTR 13

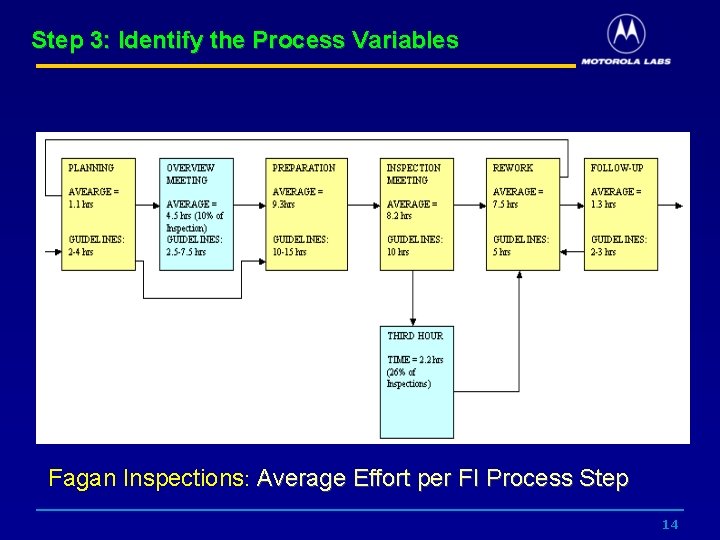
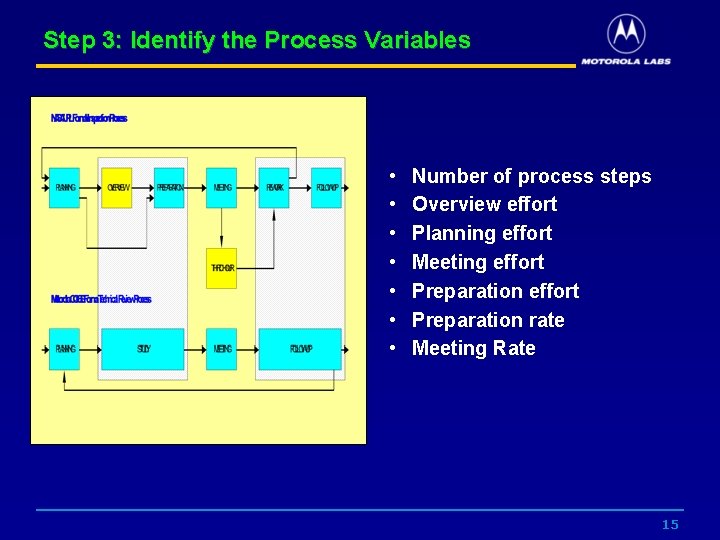
Step 3: Identify the Process Variables Fagan Inspections: Average Effort per FI Process Step 14

Step 3: Identify the Process Variables • • Number of process steps Overview effort Planning effort Meeting effort Preparation rate Meeting Rate 15

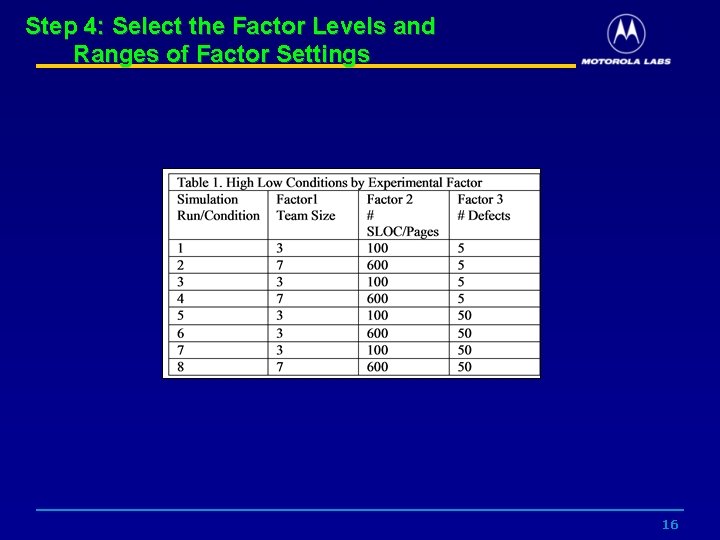
Step 4: Select the Factor Levels and Ranges of Factor Settings 16

Step 5: Select the Experimental Design • The design selected was a 23 Full Factorial that evaluates 3 input factors for inspections: • Team Size • Product Size • Estimated Fault Density • Two of these factors (team size and product size inspected) are both measurable and controllable by management. • The third factor number of initial defects is considered uncontrolled but measurable and a key factor. 17

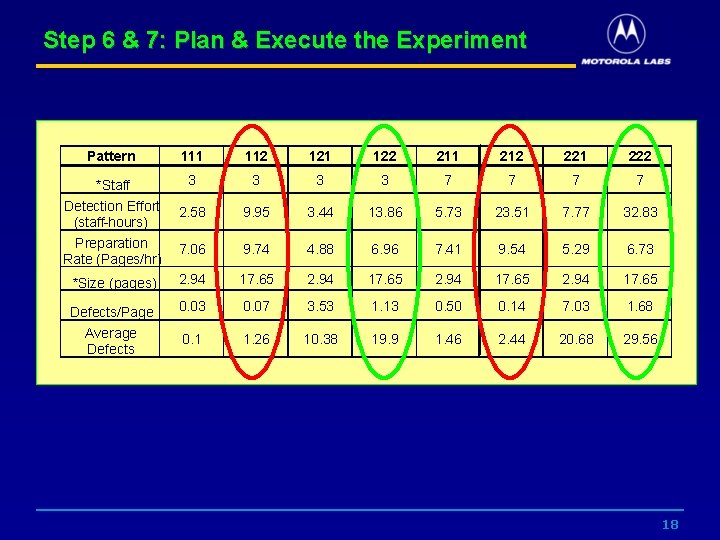
Step 6 & 7: Plan & Execute the Experiment Pattern 111 112 121 122 211 212 221 222 *Staff Detection Effort (staff-hours) Preparation Rate (Pages/hr) 3 3 7 7 2. 58 9. 95 3. 44 13. 86 5. 73 23. 51 7. 77 32. 83 7. 06 9. 74 4. 88 6. 96 7. 41 9. 54 5. 29 6. 73 *Size (pages) 2. 94 17. 65 Defects/Page Average Defects 0. 03 0. 07 3. 53 1. 13 0. 50 0. 14 7. 03 1. 68 0. 1 1. 26 10. 38 19. 9 1. 46 2. 44 20. 68 29. 56 18

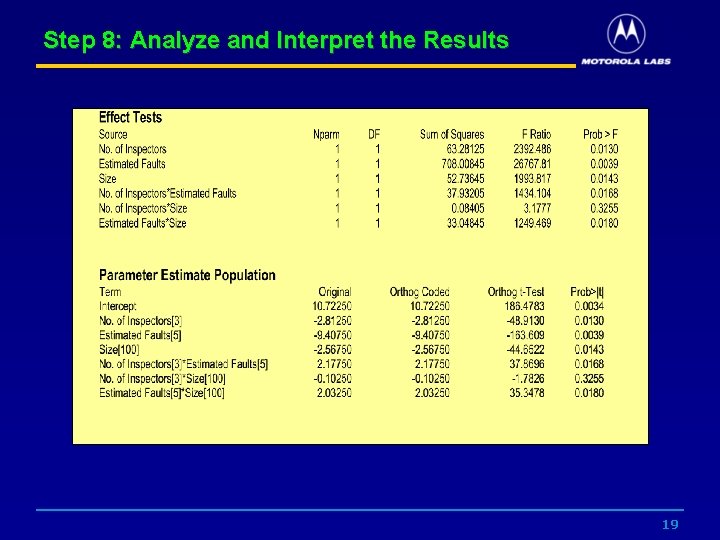
Step 8: Analyze and Interpret the Results 19

Step 8: Analyze and Interpret the Results 20

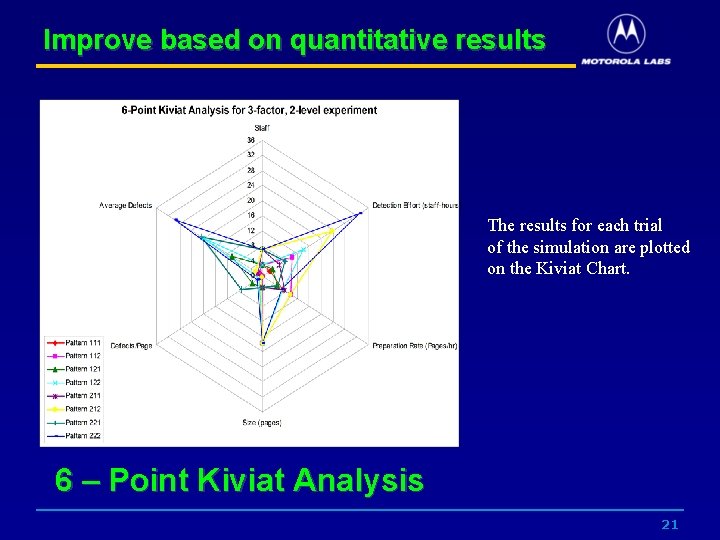
Improve based on quantitative results The results for each trial of the simulation are plotted on the Kiviat Chart. 6 – Point Kiviat Analysis 21

DMAIC: Six Sigma Methodology DEFINE • Identify customers • Define product/service scope & goals • Define expectations MEASURE CONTROL • Prevent reverting back to the old way • Control the process performance • Process mapping and analysis • Collect data from the process • Calculate sigma level ANALYSIS IMPROVE • Create solutions for the problems • Develop implementation plan • Identify gaps between current and goal performances • Prioritize opportunities to improve • Identify sources of variation 22

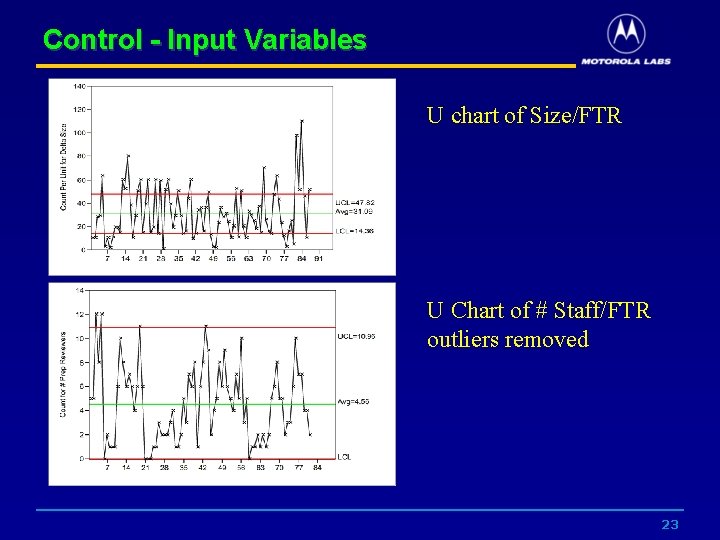
Control - Input Variables U chart of Size/FTR U Chart of # Staff/FTR outliers removed 23

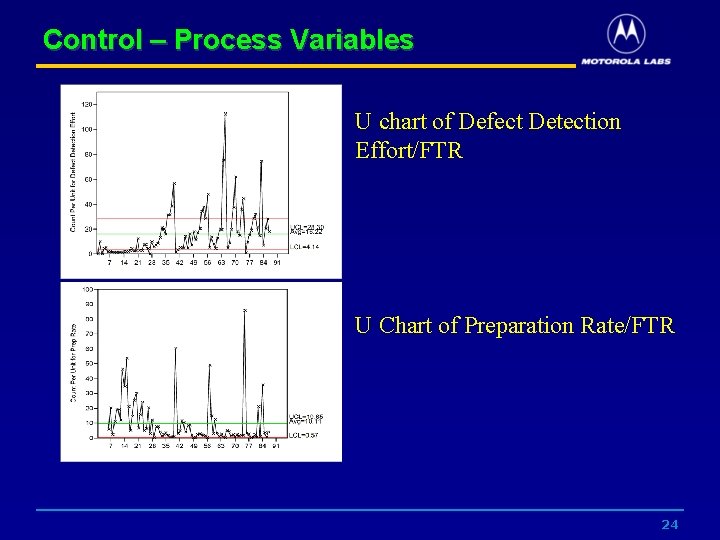
Control – Process Variables U chart of Defect Detection Effort/FTR U Chart of Preparation Rate/FTR 24

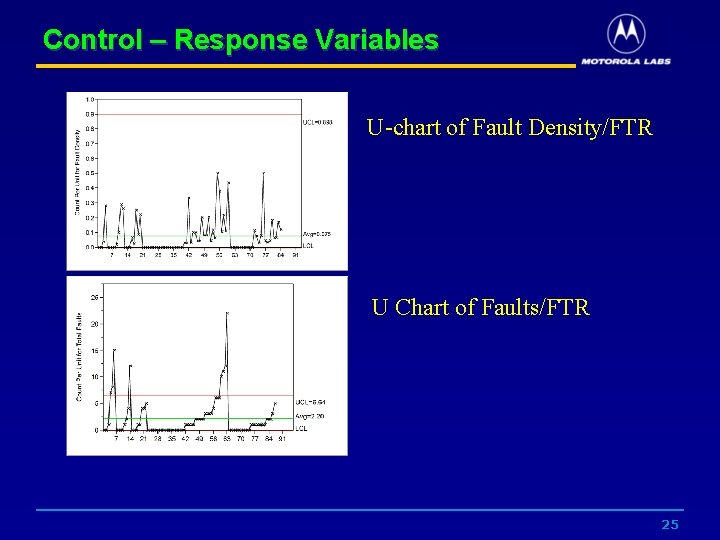
Control – Response Variables U-chart of Fault Density/FTR U Chart of Faults/FTR 25

How Do We Use SPC to Control Variation? 26

SPC and Predictability • Shewhart (1931 -1980) defined control as: “A phenomenon will be said to be controlled when, through the use of past experience, we can predict, at least within limits, how the phenomenon will vary in the future. Here it is understood that prediction within limits means that we can state, at least approximately, the probability that the observed phenomenon will fall within given limits. ” 27

SPC and Variation • Processes are executed with inherent variation • Measurements or counts collected on a process will also vary • Quantifying the process variation is key to improvement • Understanding causes of variation dictates the appropriate action in response to that variation 28

SPC and Variation • Common Causes of Variation – Any unknown or random cause of variation is a common cause – Common cause variation within predictable limits is a controlled system or constant system – Common cause variation is addressed through long-term process improvement efforts • Special Causes of Variation – Variation that is not part of the constant system is an assignable or special cause of variation – Special cause variation is an uncontrolled or unstable system – SPC specifically addresses the identification and elimination of special causes of variation 29

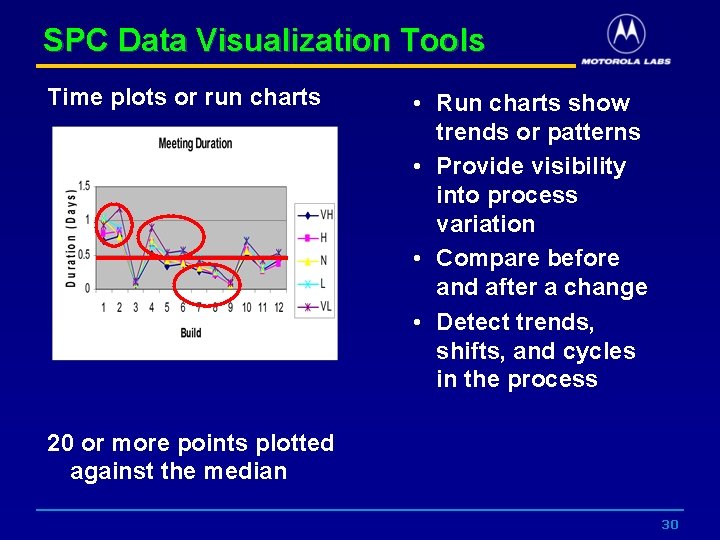
SPC Data Visualization Tools Time plots or run charts • Run charts show trends or patterns • Provide visibility into process variation • Compare before and after a change • Detect trends, shifts, and cycles in the process 20 or more points plotted against the median 30

SPC Data Visualization Tools Frequency plot or histogram • Frequency plot or histogram graphically depicts the distribution • Height of the column indicates the frequency a value occurs • Reveals the centering, spread, and variation of the data 31

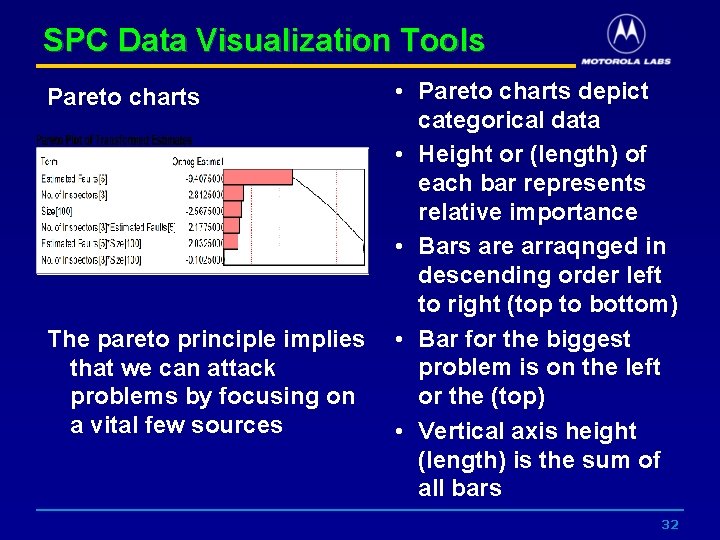
SPC Data Visualization Tools Pareto charts The pareto principle implies that we can attack problems by focusing on a vital few sources • Pareto charts depict categorical data • Height or (length) of each bar represents relative importance • Bars are arraqnged in descending order left to right (top to bottom) • Bar for the biggest problem is on the left or the (top) • Vertical axis height (length) is the sum of all bars 32

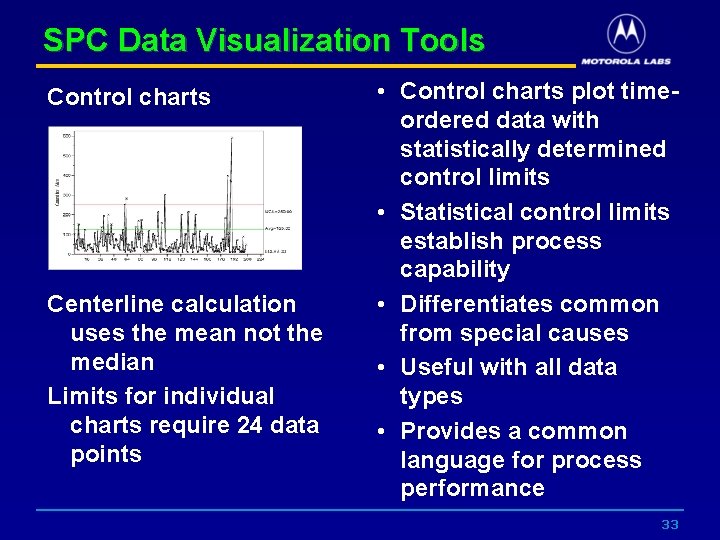
SPC Data Visualization Tools Control charts Centerline calculation uses the mean not the median Limits for individual charts require 24 data points • Control charts plot timeordered data with statistically determined control limits • Statistical control limits establish process capability • Differentiates common from special causes • Useful with all data types • Provides a common language for process performance 33

How to Construct a Control Chart • • • Select the process to be charted Determine the sampling method and plan Initiate the data collection Calculate the appropriate statistics Plot the data values on the first chart(mean, median or individuals) • Plot the range or standard deviation of the data on the second chart (only for continuous data) • Interpret the control chart and determine if the process is “in control” 34

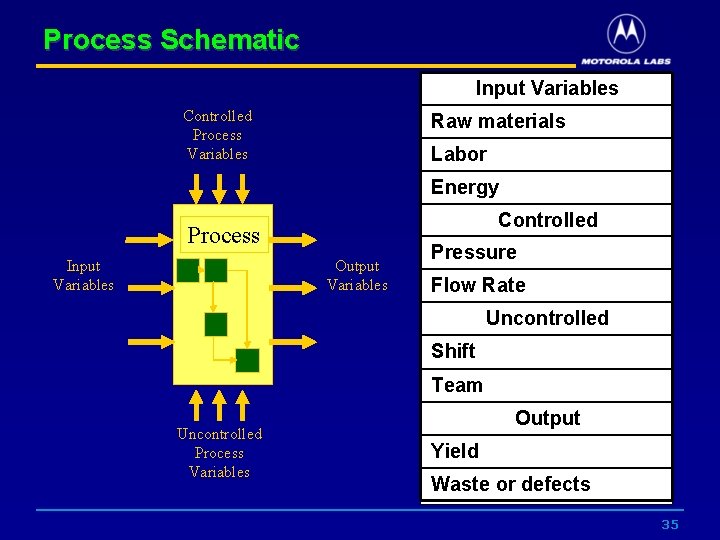
Process Schematic Input Variables Controlled Process Variables Raw materials Labor Energy Controlled Process Input Variables Output Variables Pressure Flow Rate Uncontrolled Shift Team Uncontrolled Process Variables Output Yield Waste or defects 35

Data Sampling Approach Random Sampling Stratified Random Sampling Systematic Sampling Subgroup Sampling Population or Process XXXXX XXXXX XX X Data Sample Equal chance of selection Proportionate number from each group Every nth one X 1 X 2 X 3 X 4 XXXX X 2 X 4 XXX N units every ith time, calculate a mean for each subgroup 36

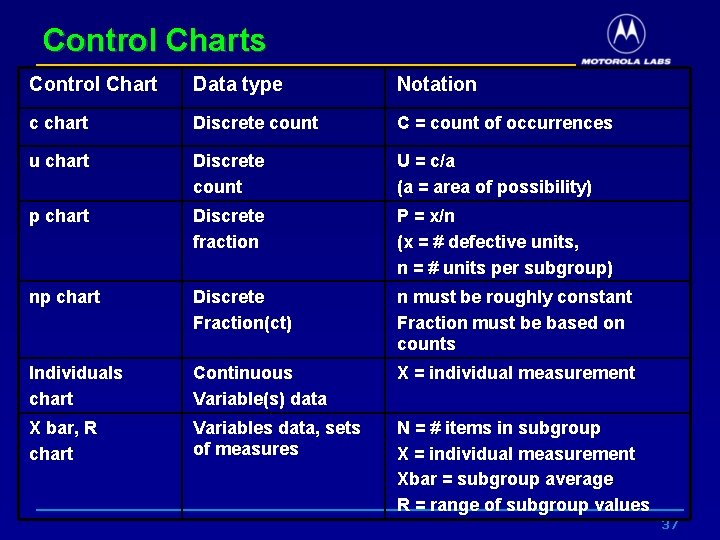
Control Charts Control Chart Data type Notation c chart Discrete count C = count of occurrences u chart Discrete count U = c/a (a = area of possibility) p chart Discrete fraction P = x/n (x = # defective units, n = # units per subgroup) np chart Discrete Fraction(ct) n must be roughly constant Fraction must be based on counts Individuals chart Continuous Variable(s) data X = individual measurement X bar, R chart Variables data, sets of measures N = # items in subgroup X = individual measurement Xbar = subgroup average R = range of subgroup values 37

Control Chart Assumptions Distribution Related Control Charts Assumptions Normal distribution Used for individuals charts, Xbar, R charts, EWMA charts Data distributed symmetrically around a mean, peak of curve at the mean Binomial distribution Used for p charts P is constant across subgroups, occurences are independent Poisson distribution Used for c charts Probability of occurence is constant, occurences are independent and rare 38

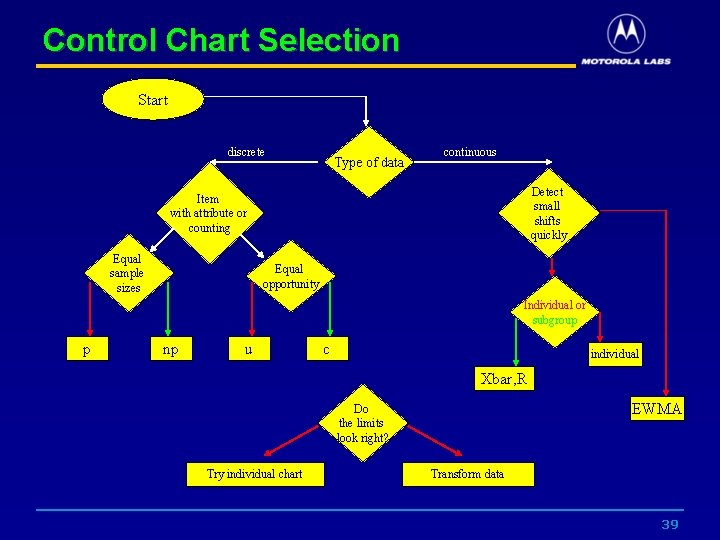
Control Chart Selection Start discrete Type of data continuous Detect small shifts quickly Item with attribute or counting Equal sample sizes Equal opportunity Individual or subgroup p np u c individual Xbar, R EWMA Do the limits look right? Try individual chart Transform data 39

Key Issues for Software • First, software engineering has a large number of key variables that have different degrees of significance depending on the process lifecycle, organizational maturity, degree of process automation, level of expertise in the domain, computational constraints on the product, required properties of the product. • Second, the individual key variables required to mirror the real world context have the potential property of extreme variance in the set of known values within the same context or across multiple contexts. For instance, programmer productivity a key variable in most empirical studies has been documented at 10: 1 and 25: 1 variances in the same context. • Third, software engineering domain variables, in combination, may create a critical mass or contextual threshold not present when studied in isolation. [1986 IEEE TSE, Basili, Selby and Hutchins] 40

Why is SPC different for software? Contributing causes for extreme variation in software measurement include: – People comprise most of the software production process – Software measurement may introduce more variation than the software process – Size metrics do not count discrete, identical units 41

Questions? 42