Accelerated Programming 2 Part I Python Programming 10

Accelerated Programming 2 Part I: Python Programming 10 Recursion © 2010 David A Watt, University of Glasgow 1

Recursive functions § A recursive function is one that calls itself. § Some programming problems can be solved using either recursion or iteration. – A recursive solution is usually more elegant (easier to write, easier to understand). – An iterative solution is usually more efficient. § Some problems are definitely solved best by using recursion. 10 -2

Example: recursion vs iteration (1) § Consider the mathematical definition of bn, where n is a non-negative integer: bn = 1 bn = b ₓ bn– 1 if n = 0 if n > 0 § This definition is recursive, and immediately suggests a recursive function: def power (b, n): if n == 0: return 1 else: return b * power(b, n-1) 10 -3

Example: recursion vs iteration (2) § Of course iteration works too: def power (b, n): p = 1 for i in range(0, n): p *= b return p § Which version is better? 10 -4

Example: recursion vs iteration (3) § Now consider this alternative definition of bn: bn = 1 bn = (bn//2)2 bn = b ₓ (bn//2)2 if n = 0 if n > 0 and n is even if n > 0 and n is odd § Note: – If n is even, n//2 = ½n. – If n is odd, n//2 = ½(n– 1). 10 -5

Example: recursion vs iteration (4) § This definition is recursive, and suggests a alternative recursive function: def power (b, n): if n == 0: return 1 else: p = power(b, n//2) if n%2 == 0: return p * p else: return b * p § This version is much more efficient, but harder to express using iteration. (Try it!) 10 -6

When does recursion work? § We must take care to ensure that a recursive function does not go on calling itself forever. § Every recursive function should have at least one “easy” case and at least one “hard” case. – In an easy case, the function does not call itself. – In a hard case, the function calls itself but only to deal with an easier case. § E. g. , recursive power function: – When n is 0, it does not call itself. – When n is non-0, it calls itself with a smaller value than n. 10 -7

Example: Towers of Hanoi (1) § Three vertical poles are mounted on a platform. § A number of discs are provided, all with different diameters. Each disc has a hole in its centre. § All discs are initially threaded on to pole 1, forming a tower with the largest disc at the bottom and the smallest disc at the top. pole 1 pole 2 pole 3 10 -8

Example: Towers of Hanoi (2) § One disc may be moved at a time, from the top of one pole to the top of another pole. § A larger disc may not be moved on top of a smaller disc. § Problem: Move the tower of discs from pole 1 to pole 2. 10 -9

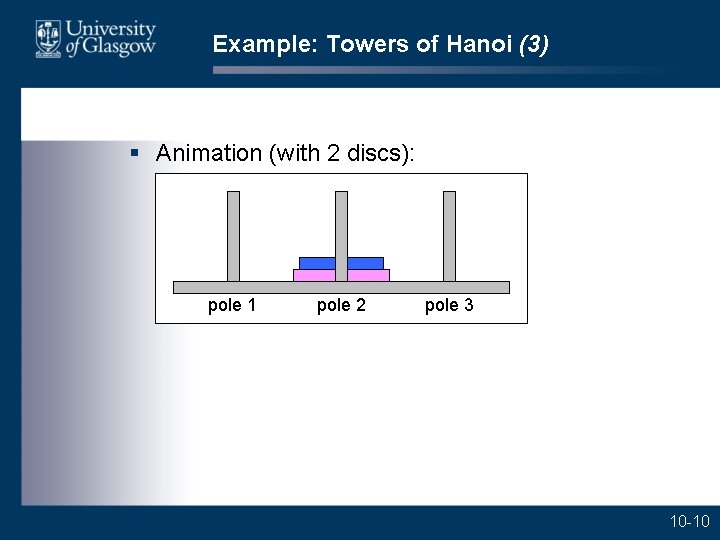
Example: Towers of Hanoi (3) § Animation (with 2 discs): pole 1 pole 2 pole 3 10 -10

Example: Towers of Hanoi (4) § Implementation: def hanoi (n): # Move a tower of n discs from tower 1 to tower 2. move_tower(n, 1, 2, 3) def move_tower (n, a, b, c): # Move a tower of n discs from the top of tower a # to the top of tower b, using tower c as a spare. if n == 1: move_disc(a, b) else: move_tower(n-1, a, c, b) move_disc(a, b) move_tower(n-1, c, b, a) 10 -11

Example: Towers of Hanoi (5) § Implementation (continued): def move_disc (a, b): # Move a single disc from tower a to tower b. print 'Move disc from %d to %d. ' % (a, b) § Output (with 3 discs): Move Move disc disc from from 1 1 2 1 3 3 1 to to 2. 3. 3. 2. 1. 2. 2. 10 -12

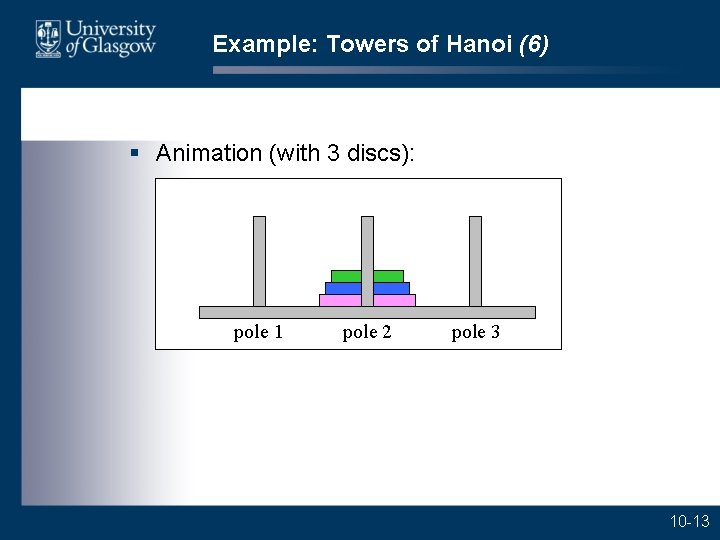
Example: Towers of Hanoi (6) § Animation (with 3 discs): pole 1 pole 2 pole 3 10 -13

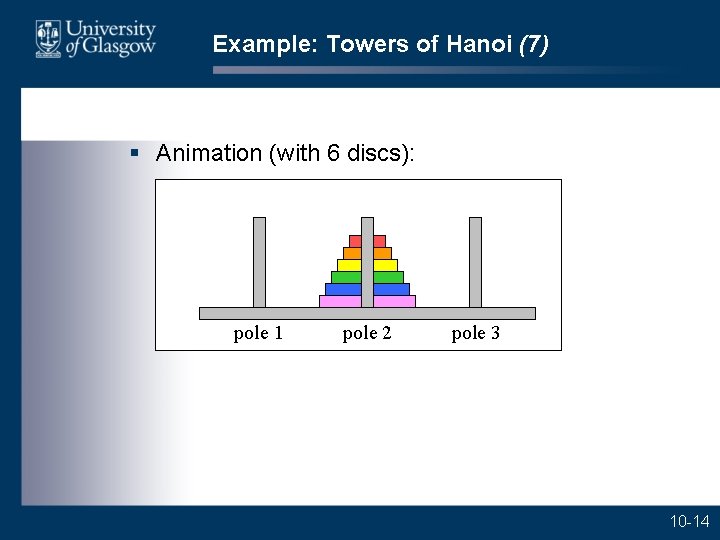
Example: Towers of Hanoi (7) § Animation (with 6 discs): pole 1 pole 2 pole 3 10 -14

Recursive data structures § A data structure is a collection of data (elements) organised in a systematic way. § A list is a data structure whose elements are organised in a sequence. § A tree is a data structure whose elements are organised in a hierarchy. Each element in a tree may have 0 or more subtrees, which are themselves trees. § Thus a tree is a recursive data structure. § Most functions on trees are naturally recursive. 10 -15

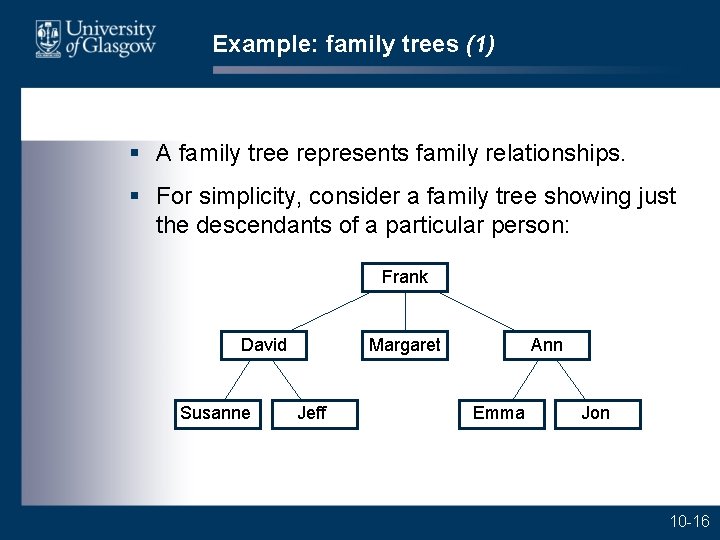
Example: family trees (1) § A family tree represents family relationships. § For simplicity, consider a family tree showing just the descendants of a particular person: Frank David Susanne Margaret Jeff Ann Emma Jon 10 -16

Example: family trees (2) § We can represent a family tree in Python by a pair (name, children), where name is a string and children is a list of (0 or more) subtrees: family = ('Frank', [ ('David', [ ('Susanne', []), ('Jeff', []) ]), ('Margaret', []), ('Ann', [ ('Emma', []), ('Jon', []) ]) ]) 10 -17

Example: family trees (3) § Simple functions on a family tree: def gen 1 (family): # Return the name of the 1 st generation of family. return family[0] def gen 2 (family): # Return a list of the names of the 2 nd generation of # family. return [child[0] for child in family[1]] § E. g. : gen 1(family) yields ‘Frank’ gen 2(family) yields [‘David’, ‘Margaret’, ‘Ann’] 10 -18

Example: family trees (4) § Function to list all members of an extended family: def all (family): # Return a list of names of all persons in the # tree family. (name, children) = family descendants = concat( [all(child) for child in children]) return [name] + descendants § This assumes: concat(ls) returns the concatenation of a list of lists ls 10 -19

Example: family trees (5) § Function to search an extended family: def search (family, name): # Search family for the person with name # and return the corresponding subtree. # Return () if name is not found. # Assume that names are unique. (fname, fchildren) = family if fname == name: return family else: return search_list(fchildren, name) 10 -20

Example: family trees (6) § Auxiliary function to search a list of children: def search_list (families, name): # Search families for the person with name # and return the corresponding subtree. # Return () if name is not found. if len(families) == 0: return () else: fam = search(families[0], name) if fam != (): return fam else: return search_list( families[1: ], name) 10 -21