Accelerated Motion A Closer Look at Average Velocity

Accelerated Motion

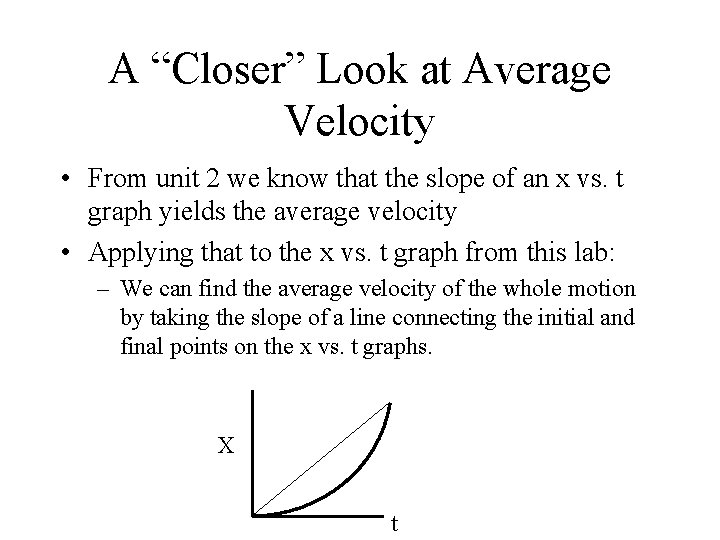
A “Closer” Look at Average Velocity • From unit 2 we know that the slope of an x vs. t graph yields the average velocity • Applying that to the x vs. t graph from this lab: – We can find the average velocity of the whole motion by taking the slope of a line connecting the initial and final points on the x vs. t graphs. X t

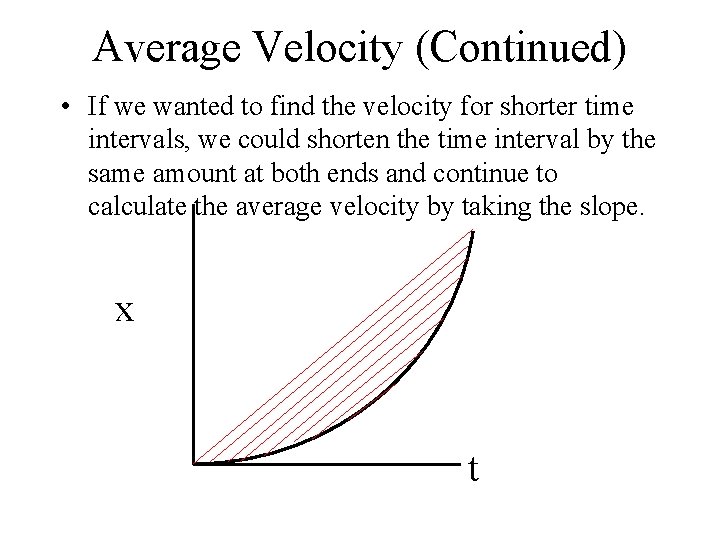
Average Velocity (Continued) • If we wanted to find the velocity for shorter time intervals, we could shorten the time interval by the same amount at both ends and continue to calculate the average velocity by taking the slope. x t

Average Velocity (Continued) • Eventually you would have a series of parallel lines with the smallest line representing a single point. • Any of the lines could replace the smallest line, therefore creating a line that is tangent to the curve at that point. • The point would be located at the midpoint (mid-time) of the original curve • Zooming in

Instantaneous Velocity • Instantaneous Velocity: The velocity of an object at an instant of time. The slope of the tangent line on an x vs. t graph. (ex. Speedometer/velocitometer? )

Average Acceleration • Average Acceleration: The change in velocity of an object in a given amount of time, or the slope of a velocity vs. time graph. Units: m/s 2 or m/s/s ex. Car (gas, brakes, steering wheel)

Nature of Acceleration • Vector or Scalar? – Slope (+ or -) – Acceleration is a vector. • Can you have a negative acceleration? – ex. slowing down while moving (+) – Speeding up while moving(-)

Nature of Acceleration • General Vector Rules – Speeding up (Acceleration vector in same direction as velocity vector) – Slowing down(Acceleration vector in opposite direction as velocity vector)

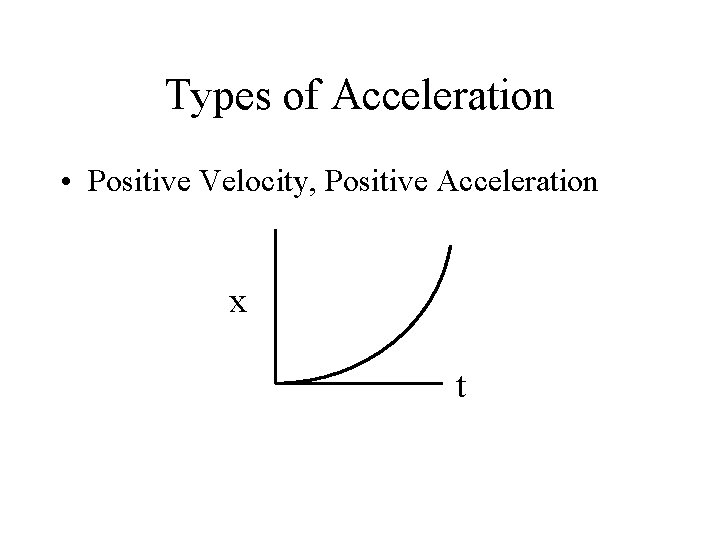
Types of Acceleration • Positive Velocity, Positive Acceleration x t

Types of Acceleration (continued) • Negative Velocity, Positive Acceleration x t

Types of Acceleration (continued) • Positive Velocity, Negative Acceleration x t

Types of Acceleration (continued) • Negative Velocity, Negative Acceleration x t

Instantaneous Acceleration • Instantaneous Acceleration: The acceleration of an object at an instant of time. The slope of the line tangent to a V vs. t graph.

Information from a Graph • X vs. T • Plots the position at point in time • Slope average velocity • Slope of Tangent instantaneous velocity

Information from a Graph (Continued) • V vs. T • Plots the velocity at a point in time • Slope average acceleration • Slope of Tangent instantaneous acceleration • Area under graph displacement ( x)

Average or Instantaneous? • What type of velocity or acceleration are we dealing with? Average or Instantaneous? • The average velocities were calculated at the midtime of an interval, therefore they are considered instantaneous. • The average accelerations were determined to be constant, if a value is constant over an interval, then the average values are equal to the instantaneous values.