Accelerated Isosurface Extraction Approach Course Visualization Modelling Presents

Accelerated Isosurface Extraction Approach Course: Visualization Modelling Presents Alex Levin International University Bremen 2006 1

Introduction International University Bremen 2006 2

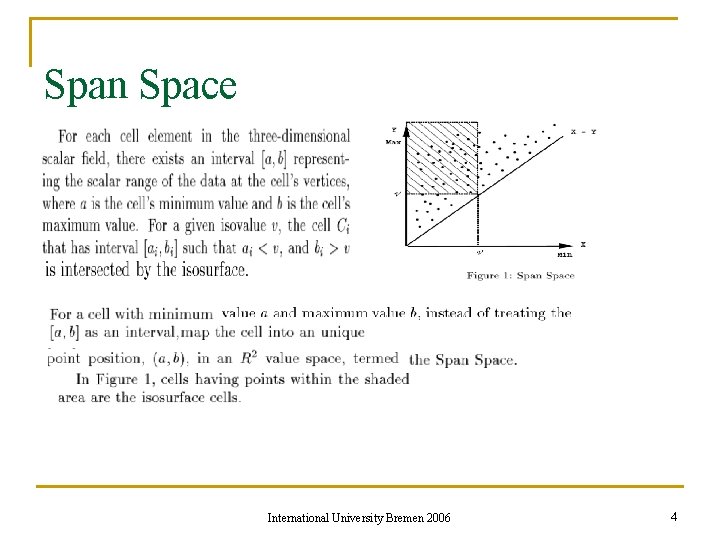
Introduction New representation, called Span Space will reduce the running time to for both structured and unstructured grids. International University Bremen 2006 3

Span Space International University Bremen 2006 4

Isosurface Extraction We deal with Accelerated Isosurface Extraction Approach [remember? ] International University Bremen 2006 5

Isosurface Extraction International University Bremen 2006 6

Isosurface Extraction International University Bremen 2006 7

Isosurface Extraction 1. 2. International University Bremen 2006 8

Isosurface Extraction International University Bremen 2006 9

Isosurface Extraction [Geometric Search Approach] International University Bremen 2006 10

Isosurface Extraction [Geometric Search Approach] International University Bremen 2006 11

Isosurface Extraction[Interval Search Approach] International University Bremen 2006 12

Isosurface Extraction[Span Space] n There is a better approach International University Bremen 2006 13

Isosurface Extraction[Span Space] International University Bremen 2006 14

Lattice (net) Subdivision International University Bremen 2006 15

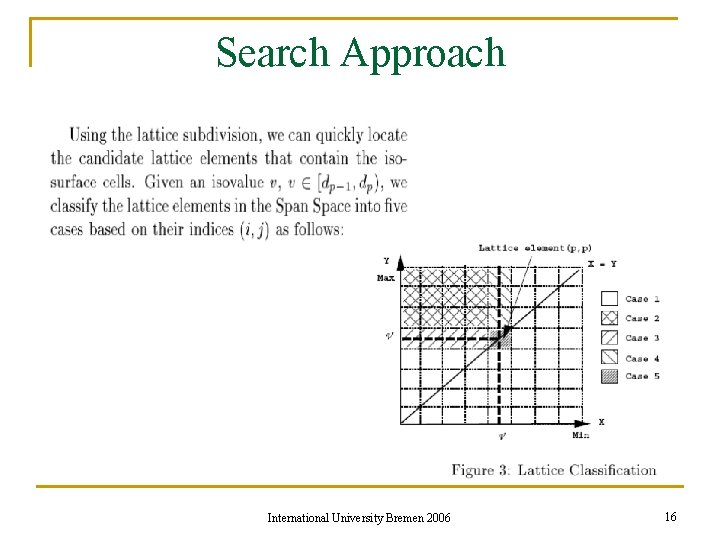
Search Approach International University Bremen 2006 16

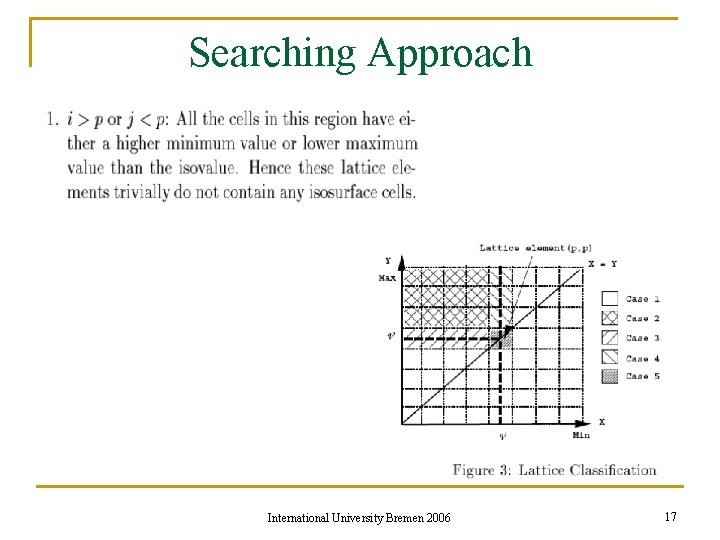
Searching Approach International University Bremen 2006 17

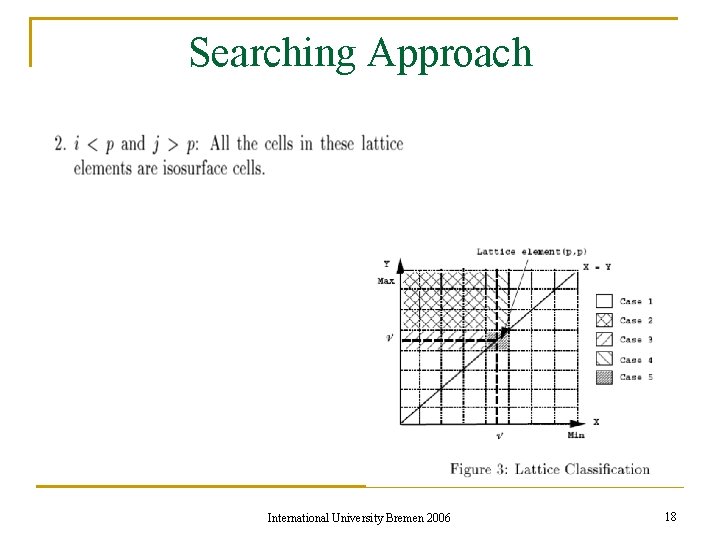
Searching Approach International University Bremen 2006 18

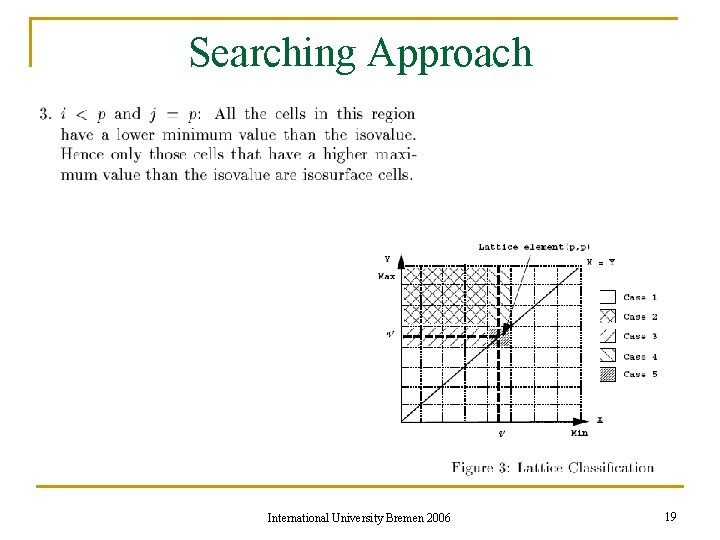
Searching Approach International University Bremen 2006 19

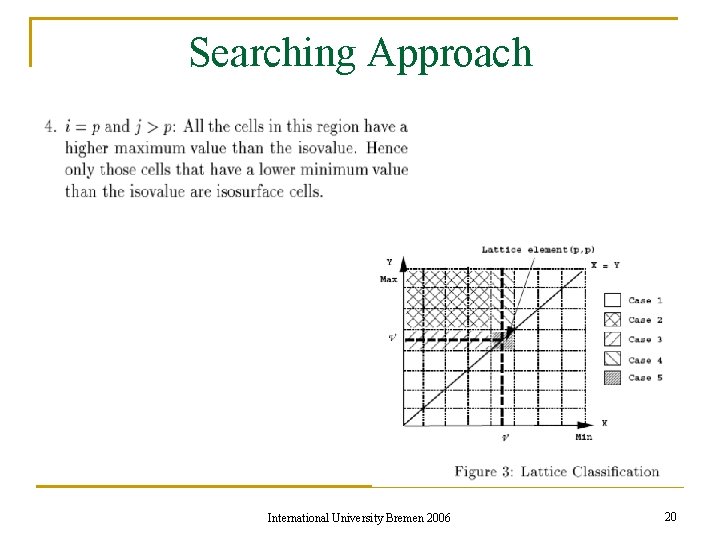
Searching Approach International University Bremen 2006 20

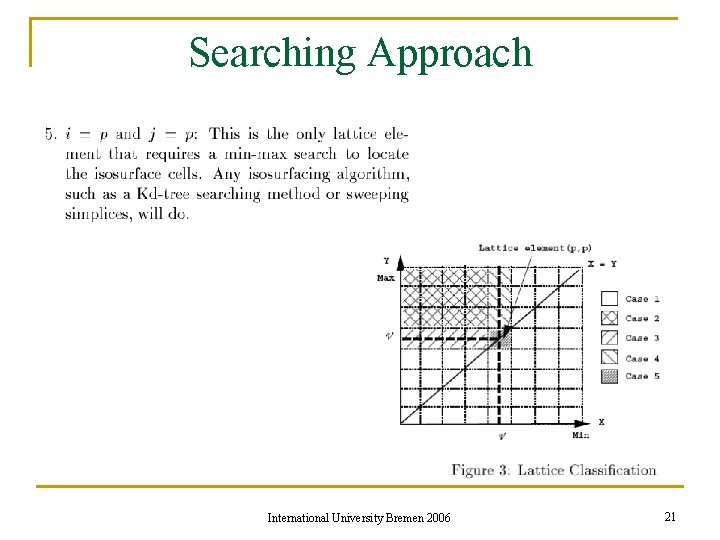
Searching Approach International University Bremen 2006 21

Searching Approach International University Bremen 2006 22

Searching Approach International University Bremen 2006 23

Searching Approach International University Bremen 2006 24

Implementation Details 1. 2. How determine the dividing points {di}? What happen with sparse dataset? -- avoid visiting empty lattice elements International University Bremen 2006 25

Implementation Details International University Bremen 2006 26

Implementation Details International University Bremen 2006 27

Implementation Details International University Bremen 2006 28

Implementation Details n To avoid this, we find di in such a way that the number of data points at each interval approximately the same. How to do it? International University Bremen 2006 29

Implementation Details n n Sort all data points into a list and divide the list into L sub-lists having approximately the same lengths. Problem!! More sub-division we have->larger number of empty lattice elements are possible. International University Bremen 2006 30

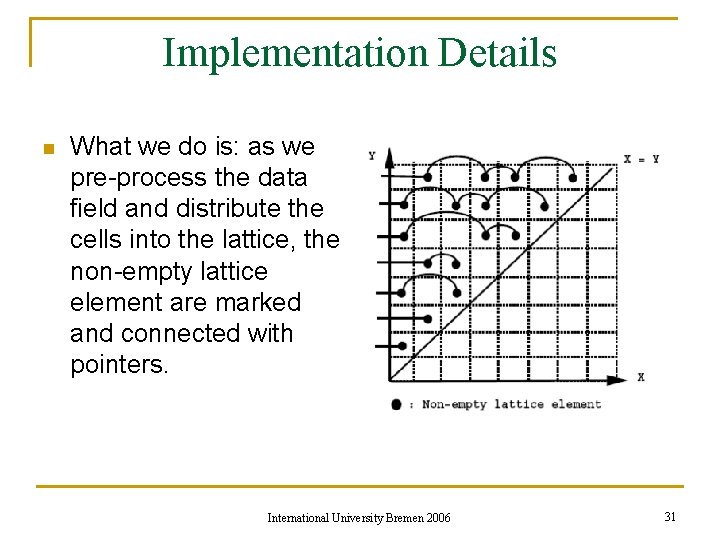
Implementation Details n What we do is: as we pre-process the data field and distribute the cells into the lattice, the non-empty lattice element are marked and connected with pointers. International University Bremen 2006 31

Parallel Algorithm Three steps: n Cell distribution phase: cells are partitioned into several sub-sets and distributed to Processing Elements [PE]. n Initialization phase: each PE build lattice, based on local data n Isosurface Extraction phase: each PE locally employs searching algorithm to extract the isosurface. International University Bremen 2006 32

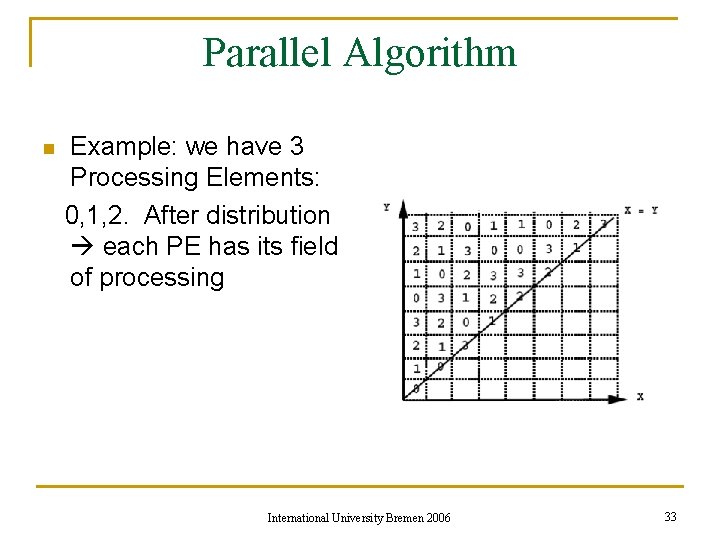
Parallel Algorithm n Example: we have 3 Processing Elements: 0, 1, 2. After distribution each PE has its field of processing International University Bremen 2006 33

Kd –tree search n n n Remember Interval Method->min and max values? ! Min & Max -> maintaining two lists May we combine 2 lists in one? Yes, using Kd-tree International University Bremen 2006 34

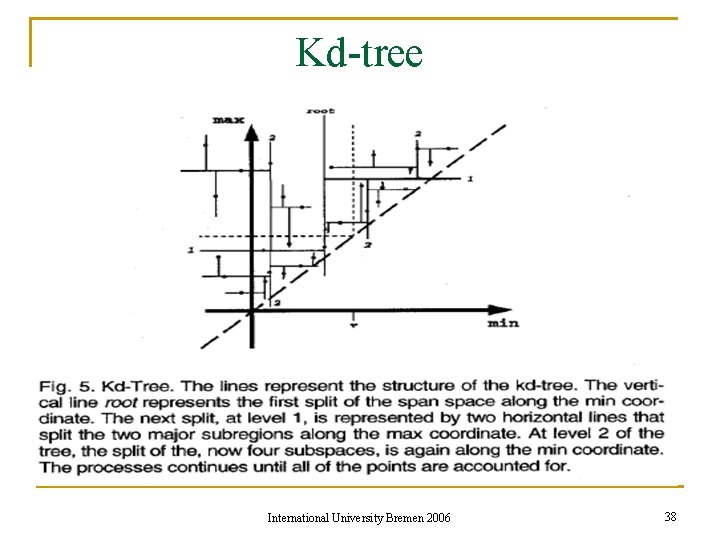
Kd-tree Introduction n A kd-tree (short for k-dimensional tree) is a space-partitioning data structure for organizing points in a k-dimensional space International University Bremen 2006 35

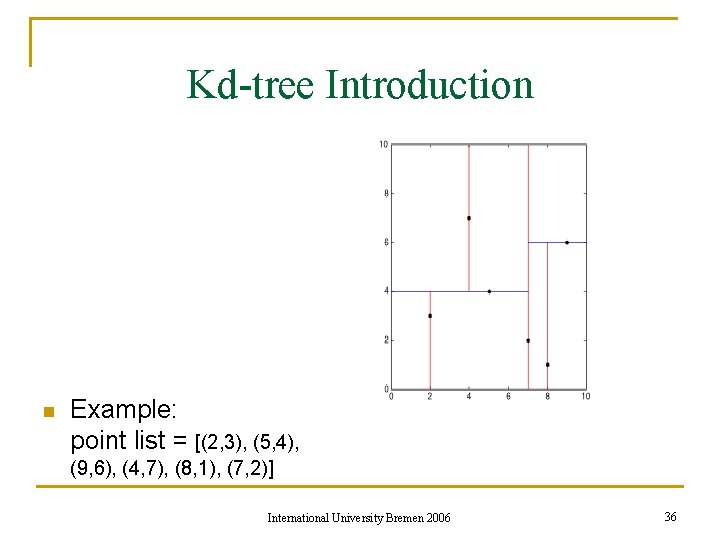
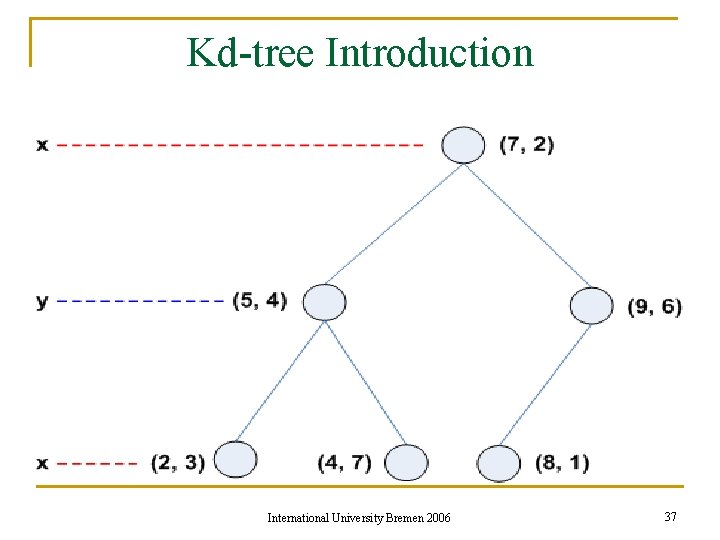
Kd-tree Introduction n Example: point list = [(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)] International University Bremen 2006 36

Kd-tree Introduction International University Bremen 2006 37

Kd-tree International University Bremen 2006 38

Construction of Kd-tree International University Bremen 2006 39

Summary n We showed that there is possibility to implement new approaches in for Extracting Span Space. International University Bremen 2006 40

References n n n Han-Wei Shen, Charles D. Hansen, Yarden Livnat, Christopher R. Johnson, Isosurfacing in Space with Utmost Efficiency (ISSUE); Yarden Livnat, Han-Wei Shen, Christopher R. Johnson, A Near Optimal Isosurface Extraction Algorithm Using the Span Space Johnson/Hnsen, The Visualization Handbook, chapter 2: Accelerated Isosurface Extraction Approaches International University Bremen 2006 41