ACC Math 1 EQ What does it mean

ACC Math 1 EQ: What does it mean for two triangles to be congruent?

Congruent figures have the same size and same shape. The parts of congruent triangles that “match” are called corresponding parts. Two polygons are congruent if ALL pairs of corresponding parts are congruent.

In a congruence statement ORDER MATTERS!!!! Everything matches up.

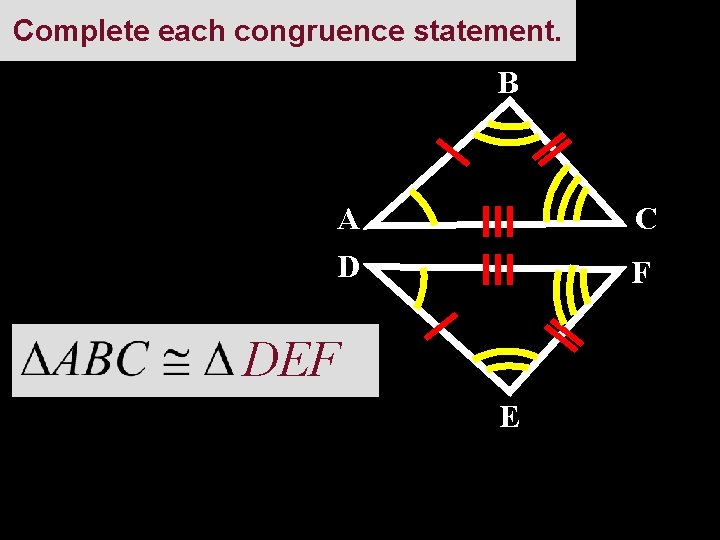
Complete each congruence statement. B A D C F DEF E

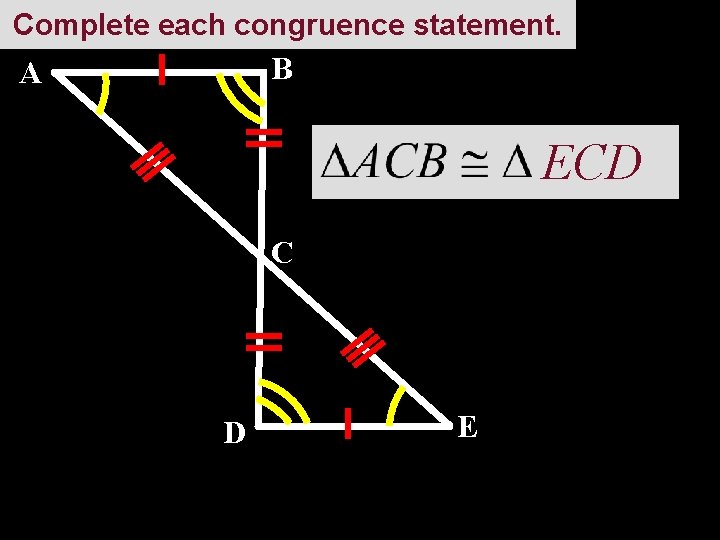
Complete each congruence statement. B A ECD C D E

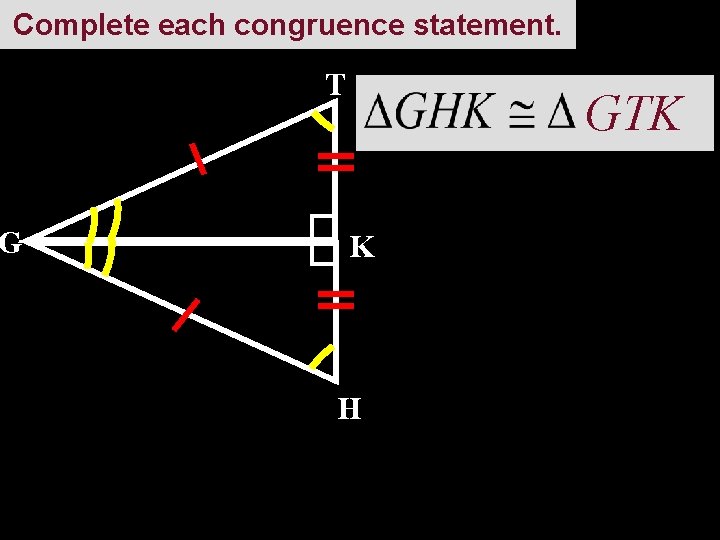
Complete each congruence statement. G T GTK K H

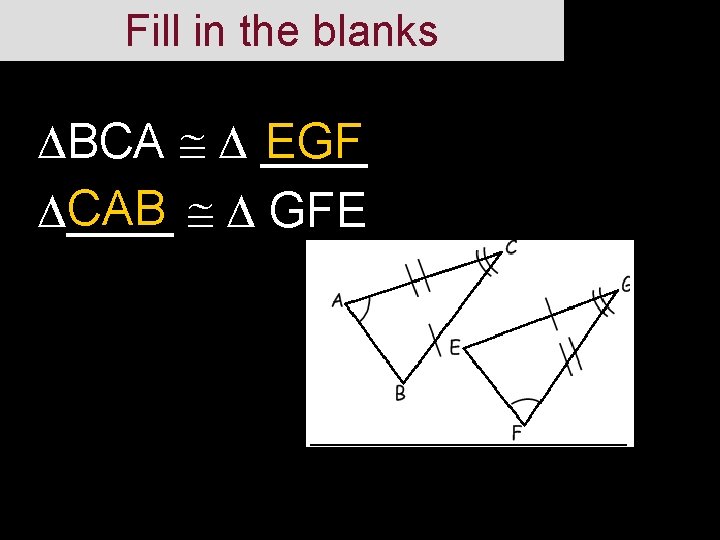
Fill in the blanks BCA ____ EGF CAB GFE ____

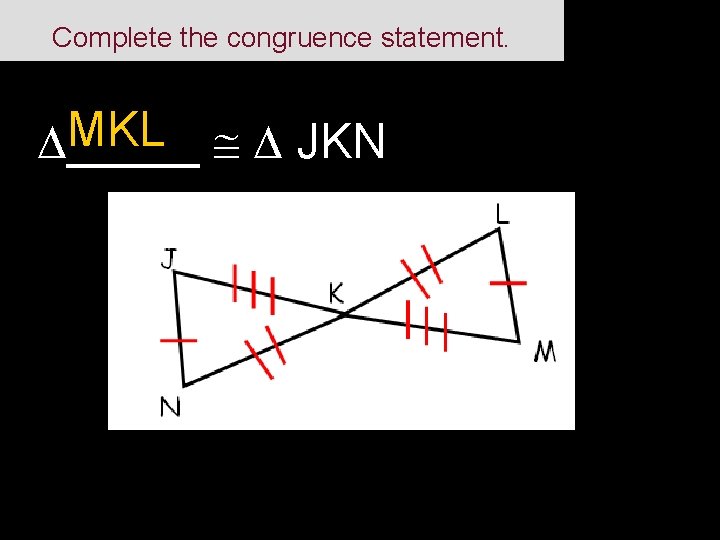
Complete the congruence statement. MKL JKN _____

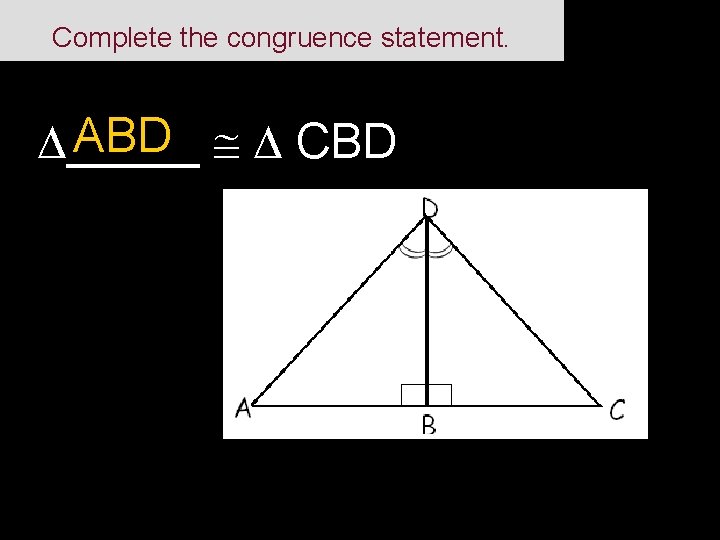
Complete the congruence statement. ABD CBD _____

Corresponding Parts of Congruent Triangles are Congruent

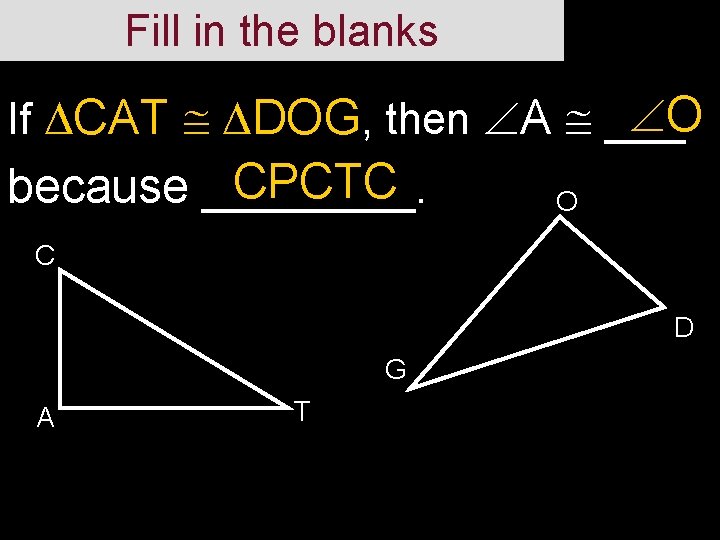
Fill in the blanks O If CAT DOG, then A ___ CPCTC because ____. O C D G A T

Fill in the blanks If FJH QRS, then ___ Q because _______. CPCTC and F ___ If XYZ ABC, then ___ CPCTC B because _______. and Y ___

Complete each congruence statement. If ABC DEF, EF then BC ___

Fill in the blanks If CAT DOG, then A ___ O.

Fill in the blanks BAT MON T N ___ ATB _____ ONM BA MO _____ NM TB ____

There are 5 ways to prove triangles congruent.

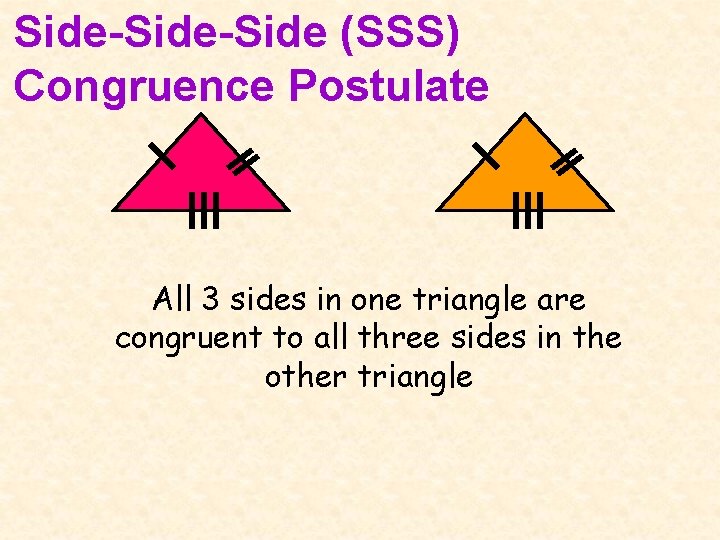
Side-Side (SSS) Congruence Postulate All 3 sides in one triangle are congruent to all three sides in the other triangle

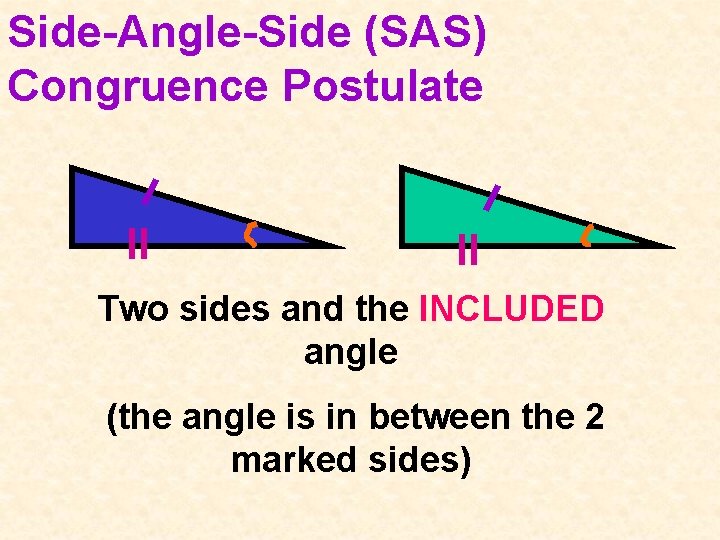
Side-Angle-Side (SAS) Congruence Postulate Two sides and the INCLUDED angle (the angle is in between the 2 marked sides)

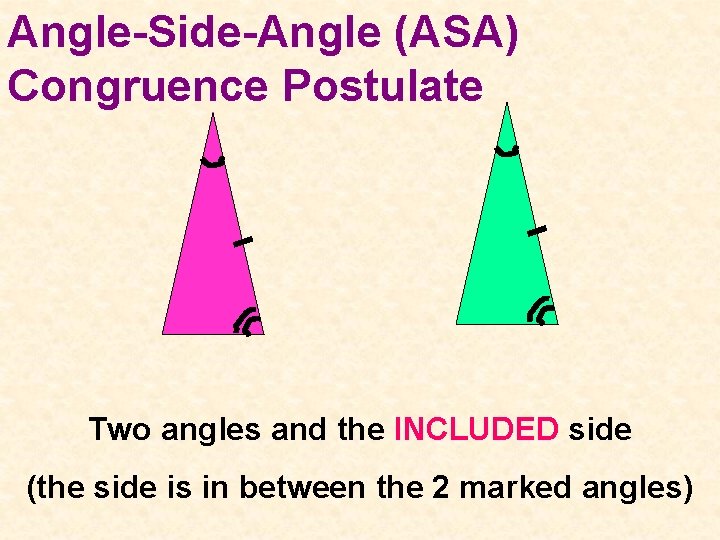
Angle-Side-Angle (ASA) Congruence Postulate Two angles and the INCLUDED side (the side is in between the 2 marked angles)

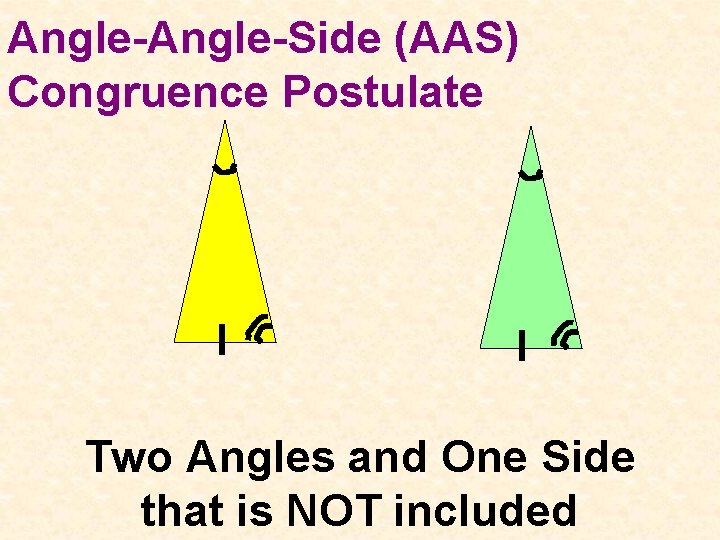
Angle-Side (AAS) Congruence Postulate Two Angles and One Side that is NOT included

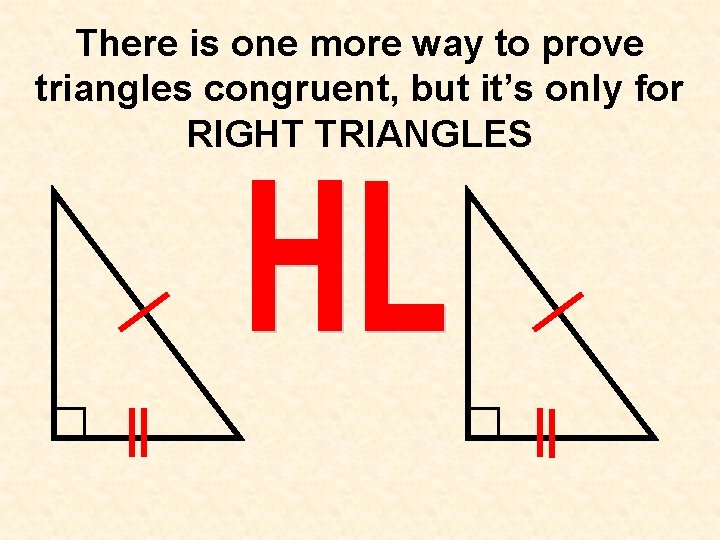
There is one more way to prove triangles congruent, but it’s only for RIGHT TRIANGLES

NO BAD WORDS Your Only Ways To Prove Triangles Are Congruent

There are only 3 types of markings YOU can add to a triangle if they are not already marked.

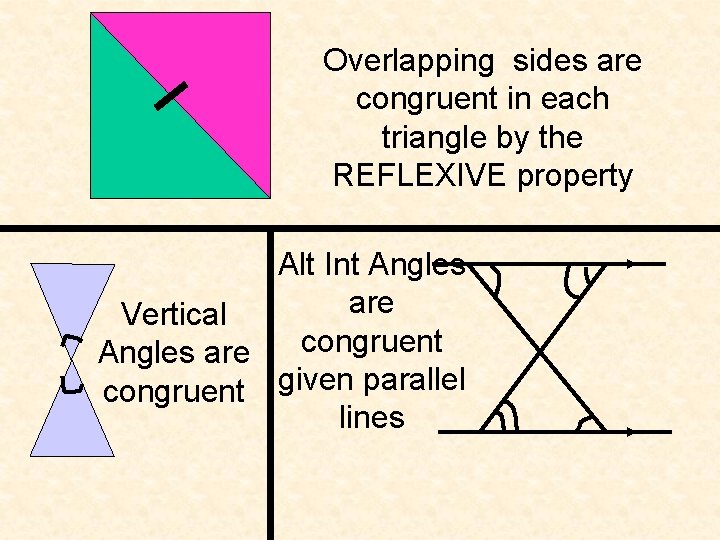
Overlapping sides are congruent in each triangle by the REFLEXIVE property Alt Int Angles are Vertical congruent Angles are congruent given parallel lines

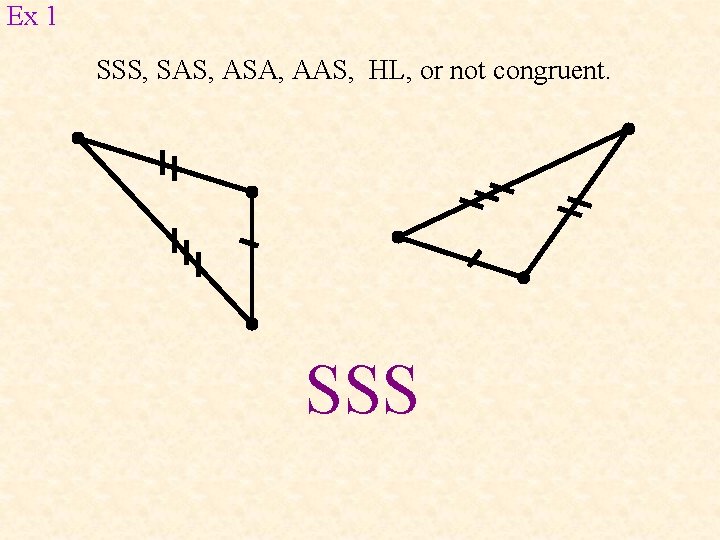
Ex 1 SSS, SAS, ASA, AAS, HL, or not congruent. SSS

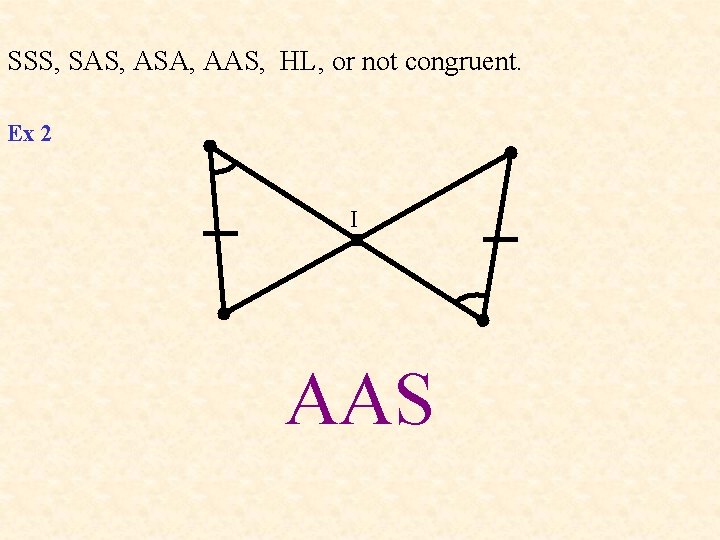
SSS, SAS, ASA, AAS, HL, or not congruent. Ex 2 I AAS

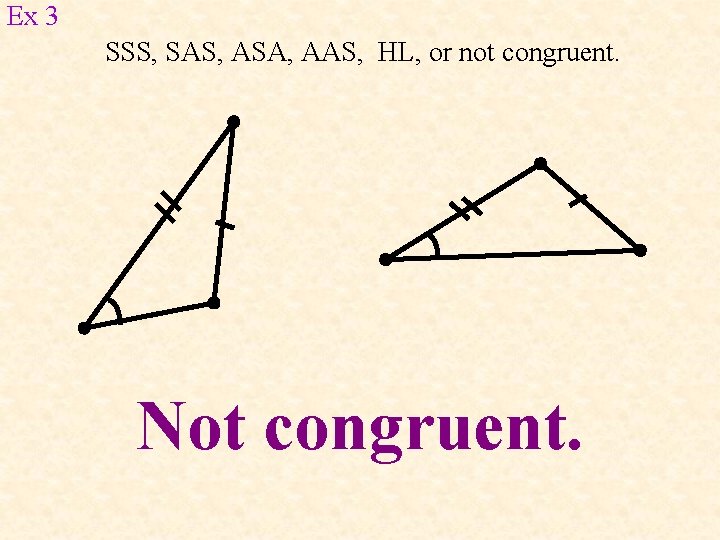
Ex 3 SSS, SAS, ASA, AAS, HL, or not congruent. Not congruent.

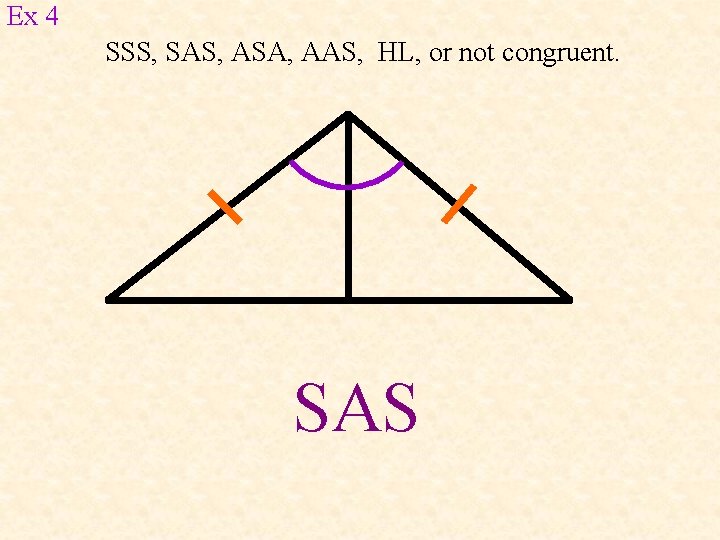
Ex 4 SSS, SAS, ASA, AAS, HL, or not congruent. SAS

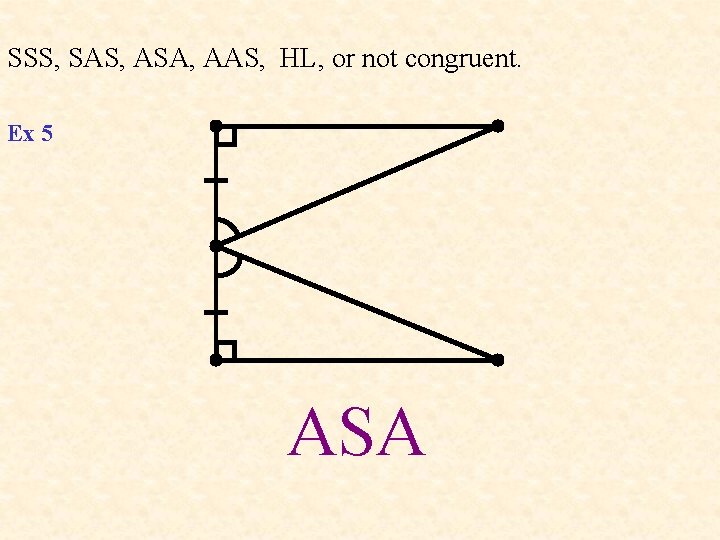
SSS, SAS, ASA, AAS, HL, or not congruent. Ex 5 ASA

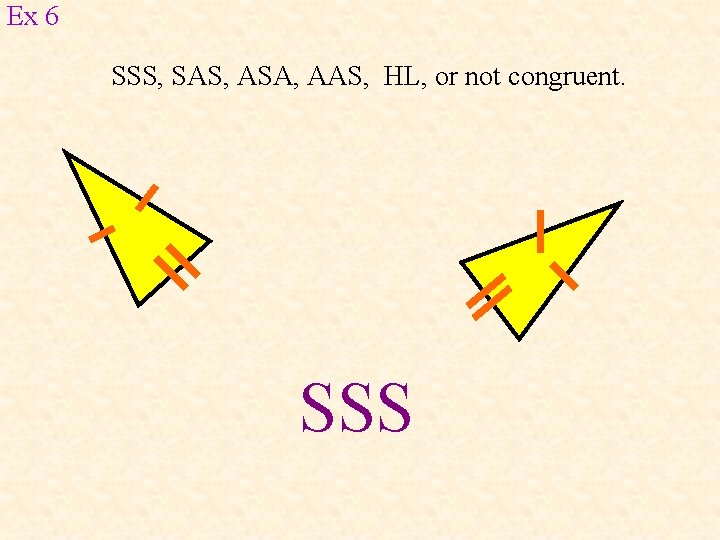
Ex 6 SSS, SAS, ASA, AAS, HL, or not congruent. SSS

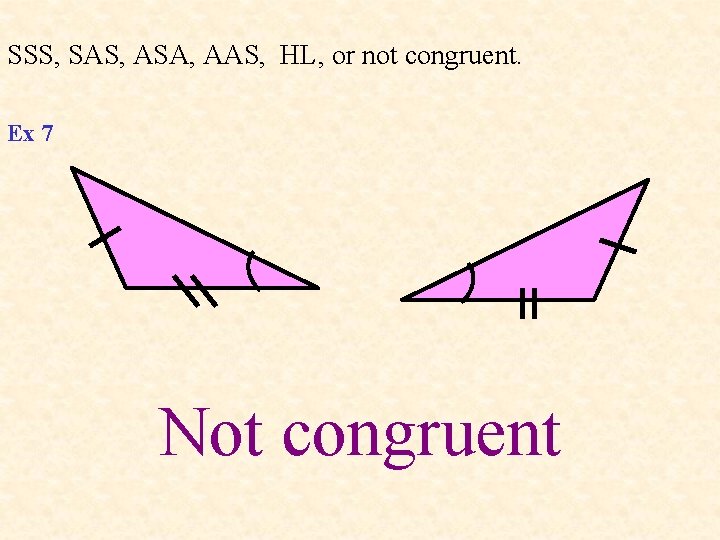
SSS, SAS, ASA, AAS, HL, or not congruent. Ex 7 Not congruent

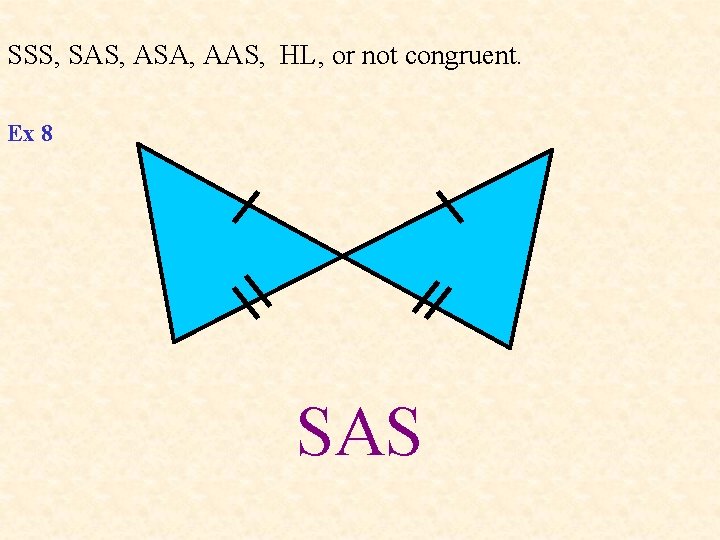
SSS, SAS, ASA, AAS, HL, or not congruent. Ex 8 SAS

Ex 9 SSS, SAS, ASA, AAS, HL, or not congruent. Not congruent.

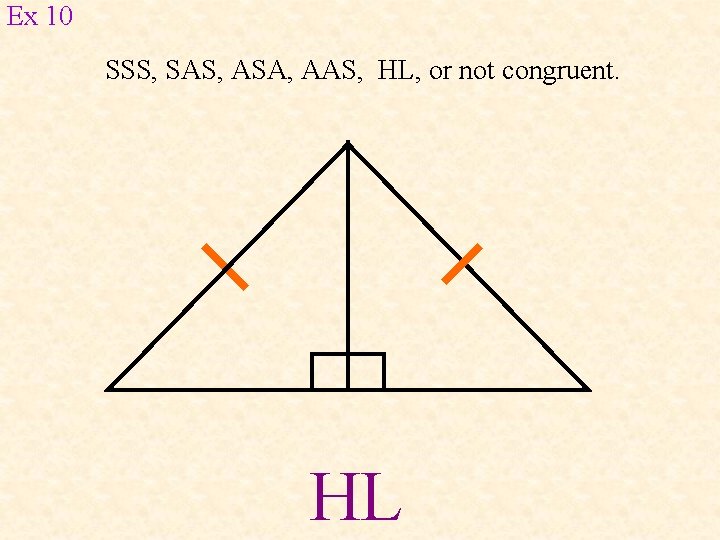
Ex 10 SSS, SAS, ASA, AAS, HL, or not congruent. HL

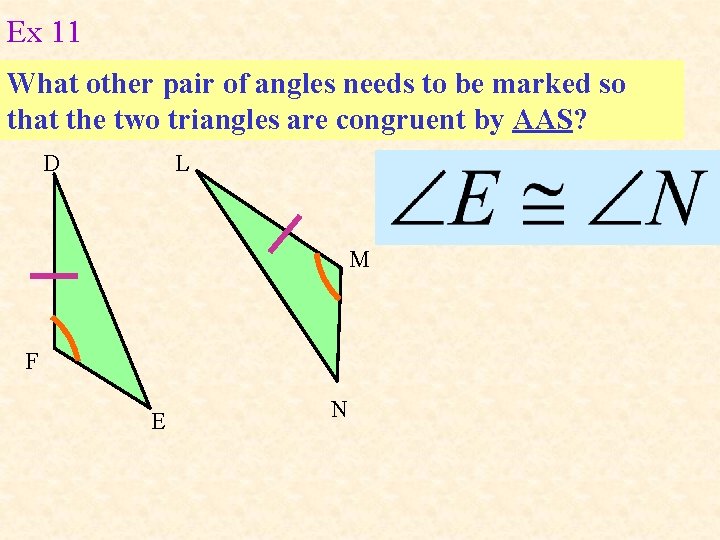
Ex 11 What other pair of angles needs to be marked so that the two triangles are congruent by AAS? D L M F E N

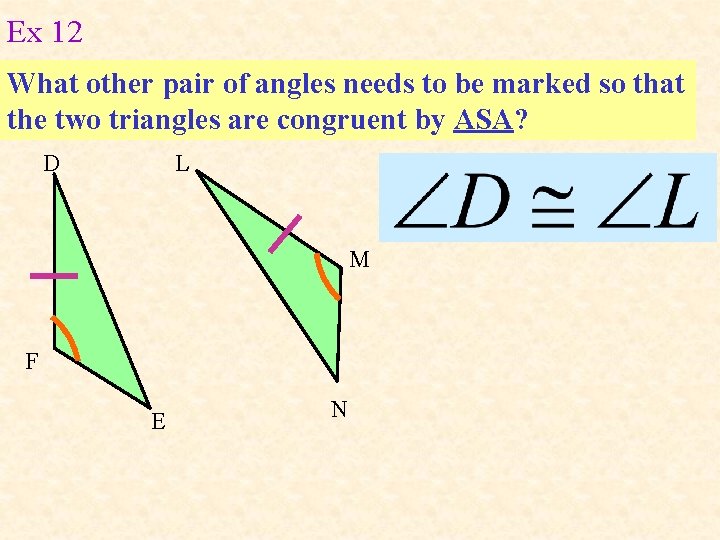
Ex 12 What other pair of angles needs to be marked so that the two triangles are congruent by ASA? D L M F E N