Academic Training Lecture 4 Nonlinear Dynamics Resonance condition

  • Slides: 20
Download presentation
Academic Training Lecture 4 : Non-linear Dynamics Resonance condition Multipole field expansion Multipole field

Academic Training Lecture 4 : Non-linear Dynamics Resonance condition Multipole field expansion Multipole field shapes Sextupole magnet Dipole magnet errors Third integer resonance Phase space trajectory for the one-third integer resonance Definition of Hamiltonian Casting the. Hamiltonian in the correct form Other interesting forms Third integer phase space Injection studies at FNAL Field around a moving cylinder of charge Beam Force Example of tracking Crossing the stochastic limit Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 1

Resonance condition Simple resonant condition This equation just defines a set of lines in

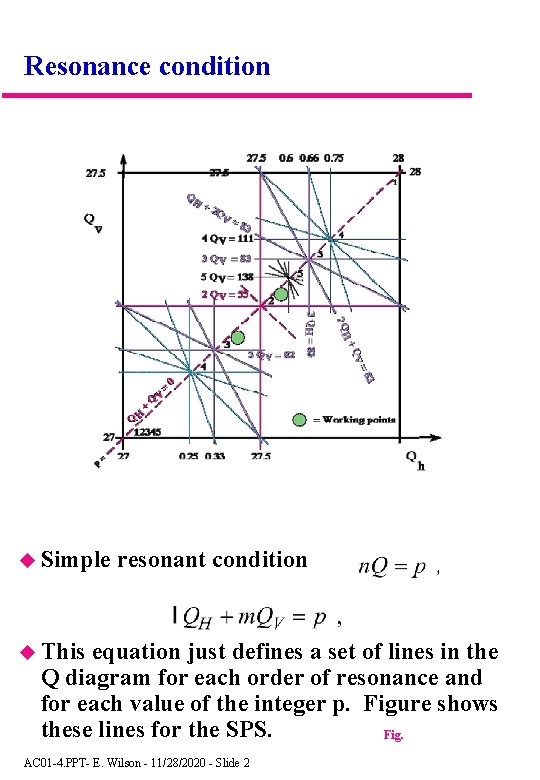
Resonance condition Simple resonant condition This equation just defines a set of lines in the Q diagram for each order of resonance and for each value of the integer p. Figure shows these lines for the SPS. Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 2

Multipole field expansion (polar) Scalar potential obeys Laplace whose solution is Example of an

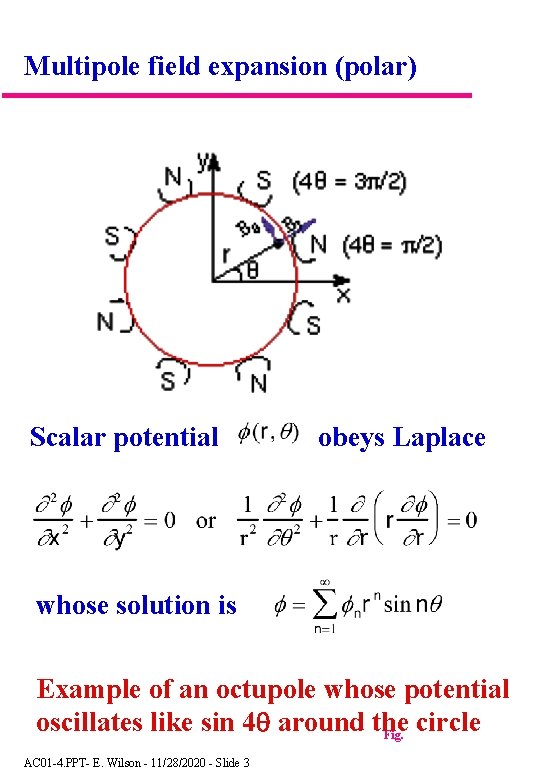
Multipole field expansion (polar) Scalar potential obeys Laplace whose solution is Example of an octupole whose potential oscillates like sin 4 around the circle Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 3

Taylor series expansion Field in polar coordinates: To get vertical field Taylor series of

Taylor series expansion Field in polar coordinates: To get vertical field Taylor series of multipoles Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 4 Fig. cas 1. 2 c

Multipole field shapes Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide

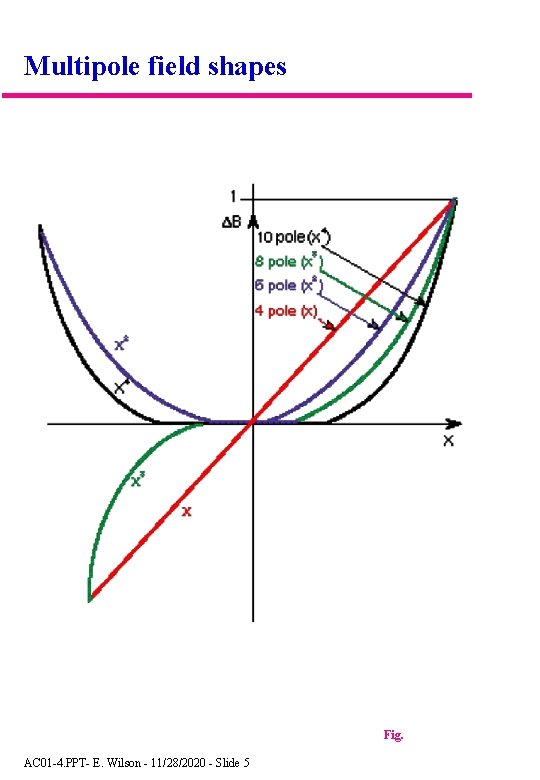
Multipole field shapes Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 5

Sextupole magnet Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 6

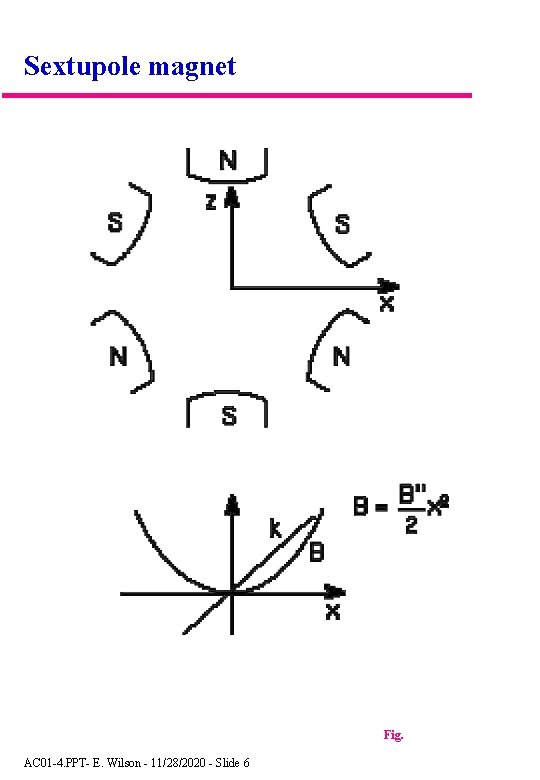
Sextupole magnet Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 6

Normal and skew sextupoles Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 -

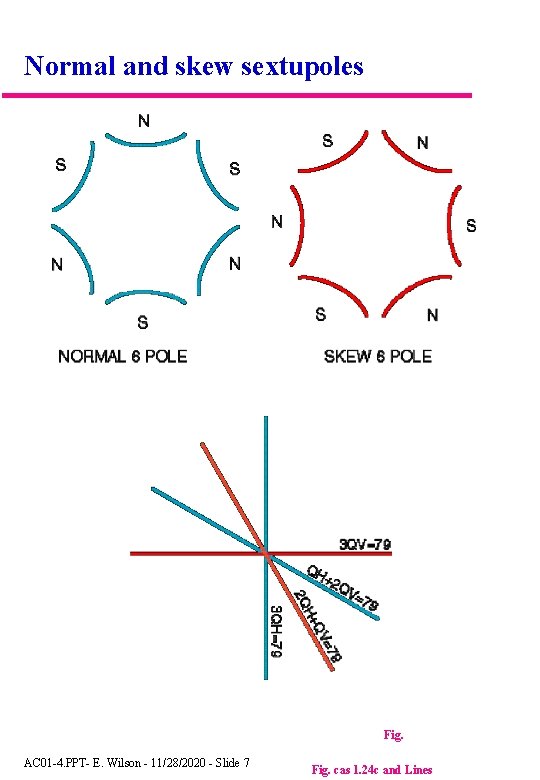
Normal and skew sextupoles Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 7 Fig. cas 1. 24 c and Lines

Dipole magnet errors The d. N and d. S poles superimposed on the magnet

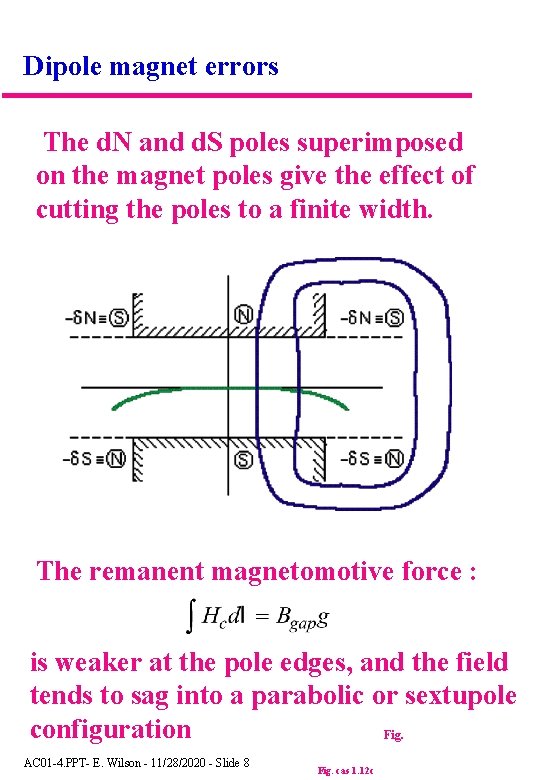
Dipole magnet errors The d. N and d. S poles superimposed on the magnet poles give the effect of cutting the poles to a finite width. The remanent magnetomotive force : is weaker at the pole edges, and the field tends to sag into a parabolic or sextupole configuration Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 8 Fig. cas 1. 12 c

Third integer resonance Substituting Incidentally Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020

Third integer resonance Substituting Incidentally Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 9

Phase space trajectory for the onethird integer resonance Fig. AC 01 -4. PPT- E.

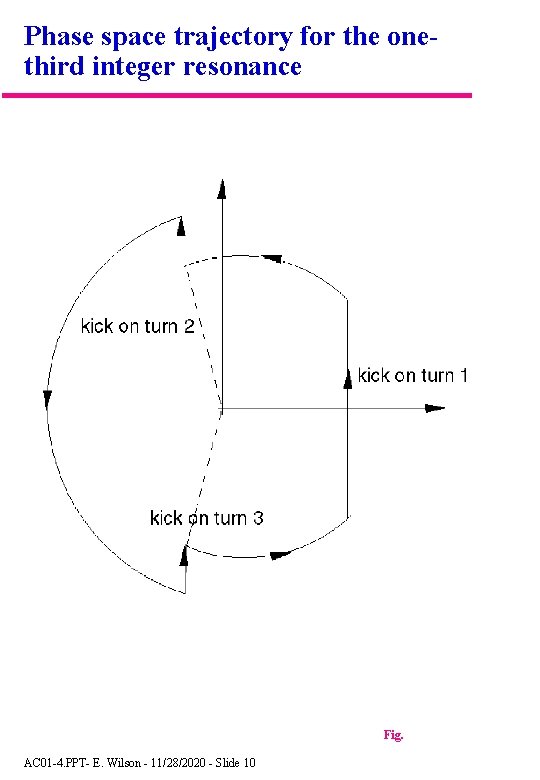
Phase space trajectory for the onethird integer resonance Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 10

Definition of Hamiltonian Any old coordinates Lagrangian Equation Define is just kinetic - potential

Definition of Hamiltonian Any old coordinates Lagrangian Equation Define is just kinetic - potential energy of motion canonical momenta Prescription Equations for Hamiltonian of motion are: Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 11

Casting the. Hamiltonian in the correct form Hamiltonian of a relativistic particle in a

Casting the. Hamiltonian in the correct form Hamiltonian of a relativistic particle in a general electromagnetic field. In our transverse ccordinates: Turn inside out to change from t to s Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 12

Other interesting forms In x plane Small divergences: But: Substitute a Taylor series: Multipoles

Other interesting forms In x plane Small divergences: But: Substitute a Taylor series: Multipoles each have a term: Quadrupoles: Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 13

Third integer phase space Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 -

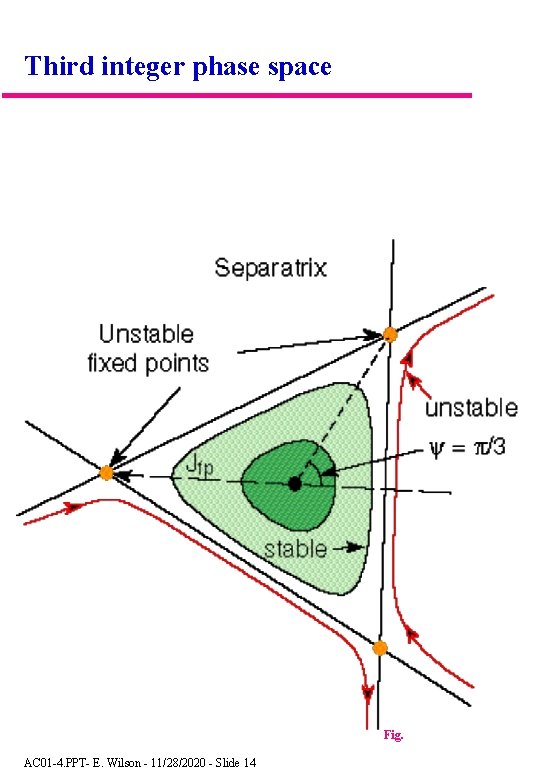
Third integer phase space Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 14

INJECTION STUDIES AT FNAL Remanent sextupole in the FNAL main ring caused serious beam

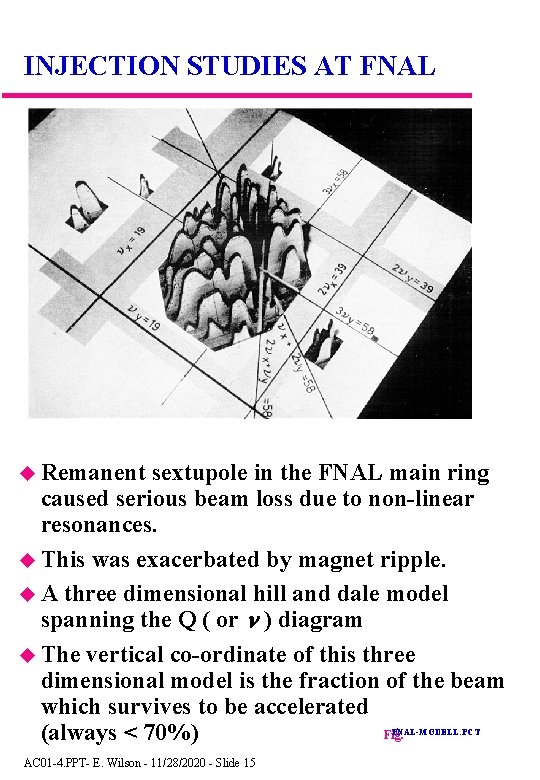
INJECTION STUDIES AT FNAL Remanent sextupole in the FNAL main ring caused serious beam loss due to non-linear resonances. This was exacerbated by magnet ripple. A three dimensional hill and dale model spanning the Q ( or ) diagram The vertical co-ordinate of this three dimensional model is the fraction of the beam which survives to be accelerated Fig. (always < 70%) FNAL-MODELL. PCT AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 15

Field around a moving cylinder of charge Take unit length of the bunch Fig.

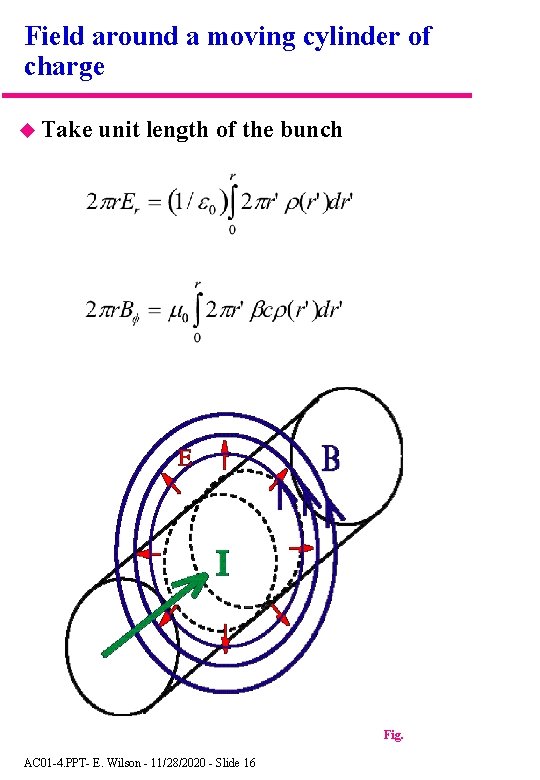
Field around a moving cylinder of charge Take unit length of the bunch Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 16

Beam Force Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 17

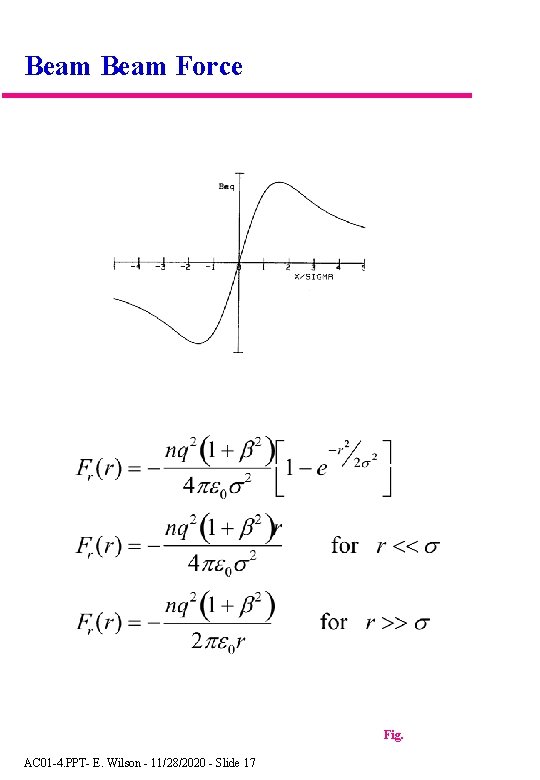
Beam Force Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 17

Example of tracking Below the beam-beam limit and without tune modulation we see the

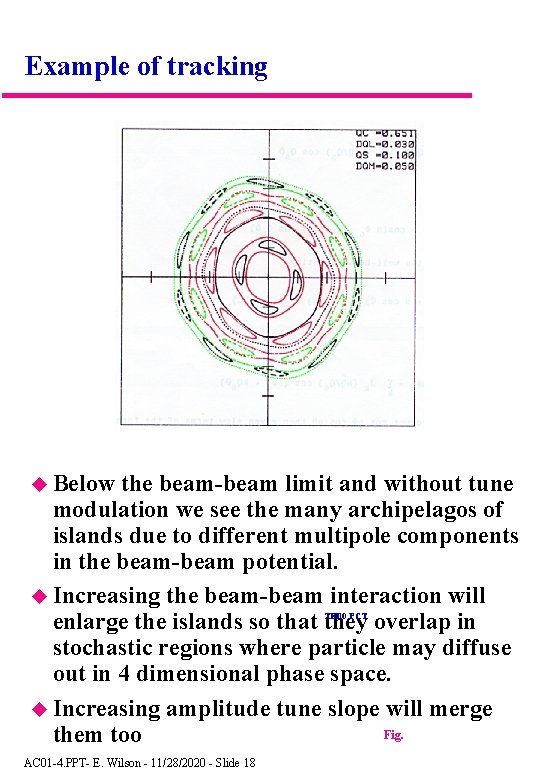
Example of tracking Below the beam-beam limit and without tune modulation we see the many archipelagos of islands due to different multipole components in the beam-beam potential. Increasing the beam-beam interaction will enlarge the islands so that they overlap in stochastic regions where particle may diffuse out in 4 dimensional phase space. Increasing amplitude tune slope will merge Fig. them too TED 0. PCT AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 18

Crossing the stochastic limit Increasing Q shift causes islands to merge in a stochastic

Crossing the stochastic limit Increasing Q shift causes islands to merge in a stochastic sea of chaos Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 19

Summary : Non-linear Dynamics Resonance condition Multipole field expansion Multipole field shapes Sextupole magnet

Summary : Non-linear Dynamics Resonance condition Multipole field expansion Multipole field shapes Sextupole magnet Dipole magnet errors Third integer resonance Phase space trajectory for the one-third integer resonance Definition of Hamiltonian Casting the. Hamiltonian in the correct form Other interesting forms Third integer phase space Injection studies at FNAL Field around a moving cylinder of charge Beam Force Example of tracking Crossing the stochastic limit Fig. AC 01 -4. PPT- E. Wilson - 11/28/2020 - Slide 20

l l waiteventqueue condition waiteventinterruptiblequeue condition waiteventtimeoutqueue conditionl l waiteventqueue condition waiteventinterruptiblequeue condition waiteventtimeoutqueue condition
Nonlinear Sampling Nonlinear Sampling st Memoryless nonlinear distortionNonlinear Sampling Nonlinear Sampling st Memoryless nonlinear distortion
Operational Amplifier NonLinear NonLinear Applications Nonlinear application isOperational Amplifier NonLinear NonLinear Applications Nonlinear application is
academic transfer academic transfer plan academic transfer academicacademic transfer academic transfer plan academic transfer academic
Resonance Lecture 10 Resonance 3 Types Pharyngeal OralResonance Lecture 10 Resonance 3 Types Pharyngeal Oral
Lecture 37 Nuclear magnetic resonance Nuclear magnetic resonanceLecture 37 Nuclear magnetic resonance Nuclear magnetic resonance
MODELING SolutionPhase Nonlinear Dynamics Heterogeneous Dynamics 1 BriefMODELING SolutionPhase Nonlinear Dynamics Heterogeneous Dynamics 1 Brief
Beam dynamics in accelerators nonlinear dynamics and experimentsBeam dynamics in accelerators nonlinear dynamics and experiments
Nonlinear Dynamics of the Collector Ring Beam DynamicsNonlinear Dynamics of the Collector Ring Beam Dynamics
MODELING SolutionPhase Nonlinear Dynamics Heterogeneous Dynamics 1 BriefMODELING SolutionPhase Nonlinear Dynamics Heterogeneous Dynamics 1 Brief
Lecture 4 Nonlinear price discrimination Nonlinear prices InLecture 4 Nonlinear price discrimination Nonlinear prices In
Nonlinear Planning Lecture Module 9 Nonlinear Planning withNonlinear Planning Lecture Module 9 Nonlinear Planning with
Nuclear Magnetic Resonance A Introduction Nuclear Magnetic ResonanceNuclear Magnetic Resonance A Introduction Nuclear Magnetic Resonance
Resonance and Standing Waves Resonance Every object hasResonance and Standing Waves Resonance Every object has
Resonance and Formal Charge 1 Resonance and FormalResonance and Formal Charge 1 Resonance and Formal
Open Pipe Resonance Sound Quality Open Pipe ResonanceOpen Pipe Resonance Sound Quality Open Pipe Resonance
Nuclear Magnetic Resonance A Introduction Nuclear Magnetic ResonanceNuclear Magnetic Resonance A Introduction Nuclear Magnetic Resonance
Magnetic Resonance Imaging Magnetic resonance started out asMagnetic Resonance Imaging Magnetic resonance started out as
Magnetic Resonance Imaging MRI and Magnetic Resonance SpectroscopyMagnetic Resonance Imaging MRI and Magnetic Resonance Spectroscopy