ACADEMIA DE STUDII ECONOMICE BUCURETI FACULTATEA DE RELAII

ACADEMIA DE STUDII ECONOMICE BUCUREŞTI FACULTATEA DE RELAŢII ECONOMICE INTERNAŢIONALE “Finanţare internaţională” CURSUL IV: “Teoria portofoliilor financiare internaţionale” Conf. dr Cristian PĂUN

Sursa de incertitudine şi risc: • imperfecţiunea informaţiei; • imposibilitatea unor predicţii corecte cu privire la even. viitoare; • incapacitatea de a identifica toate alternativele decizionale; • evenimentele viitoare sunt adesea unice; • profilul investitorilor; • imposibilitatea de a controla toţi factorii care pot afecta decizia; • presiunea timpului. Relaţia dintre risc şi câştigul aşteptat: • risc mai mare implică un câştig aşteptat mai mare • relaţia dintre utilitatea câştigului aşteptat al unei investiţii şi câştig nu este una liniară (utilitatea marginală descrescândă u (w)>0 şi u (w)<0) – Bernoulli) • dacă un investitor preferă o investiţie p în locul unei investiţii q înseamnă că pentru el U(p) este mai mare decât U(q) – Neumann & Morgenstern Course 3: International Financial Portfolios Theory 2

Ipotezele de bază ale modelului Markovitz: 1. Profitul aşteptat este distribuit normal; 2. Investitorii caută în fiecare moment maximizarea utilităţii lor; 3. Investitorii au o utilitate marginală descrescândă pentru capitalul lor; 4. Volatilitatea câştigurilor probabile dă dimensiunea riscului plasamentului; 5. Decizia de plasament este bazată pe profilul risc - câştig; 6. Investitorii vor prefera întotdeauna alternativele de plasament mai profitabile la un nivel dat al riscului; 7. Investitorii vor prefera întotdeauna alternativele de plasament mai puţin riscant la un nivel dat al câştigului aşteptat; 8. Investitorii au un timp limitat pentru decizia lor de plasament. Course 3: International Financial Portfolios Theory 3

Câştigul aşteptat al unui titlu / portofoliu - Ipoteza iniţială Course 3: International Financial Portfolios Theory 4
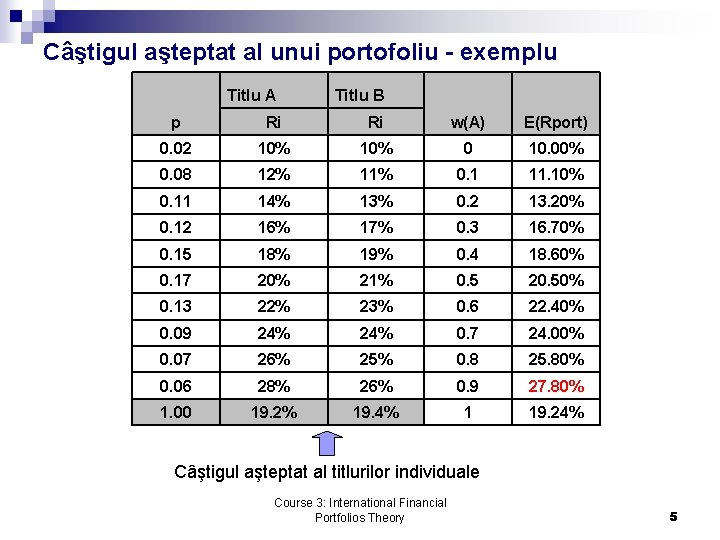
Câştigul aşteptat al unui portofoliu - exemplu Titlu A Titlu B p Ri Ri w(A) E(Rport) 0. 02 10% 0 10. 00% 0. 08 12% 11% 0. 1 11. 10% 0. 11 14% 13% 0. 2 13. 20% 0. 12 16% 17% 0. 3 16. 70% 0. 15 18% 19% 0. 4 18. 60% 0. 17 20% 21% 0. 5 20. 50% 0. 13 22% 23% 0. 6 22. 40% 0. 09 24% 0. 7 24. 00% 0. 07 26% 25% 0. 8 25. 80% 0. 06 28% 26% 0. 9 27. 80% 1. 00 19. 2% 19. 4% 1 19. 24% Câştigul aşteptat al titlurilor individuale Course 3: International Financial Portfolios Theory 5

Varianţa, covarianţa şi corelaţia Măsura riscului în cazul unui titlu individual Proprietăţile varianţei: 1. var (constant)= 0 2. var (c x z) = c 2 x var (z) 3. var (x + y) = var (x) + var (y) + cov (x, y) Course 3: International Financial Portfolios Theory 6

Varianţa, covarianţa şi corelaţia (cont. ) Proprietăţile covarianţei: 1. cov(y, xi)= c 1*cov(y, x 1)+c 2* cov(y, x 2)+. . . cn* cov(y, xn) when y= c 1*x 1+c 2*x 2+. . . cn*xn 2. cov(x, y) = cov(y, x) 3. cov(c * x, y)=c*cov(x, y) Interpretare: • correl(x, y) = 0 – x este independent de y • correl(x, y)=1 – x corelat pozitiv perfect cu y • correl(x, y) – negativ indică relaţie de inversă proporţionalitate între cei doi termeni Course 3: International Financial Portfolios Theory 7
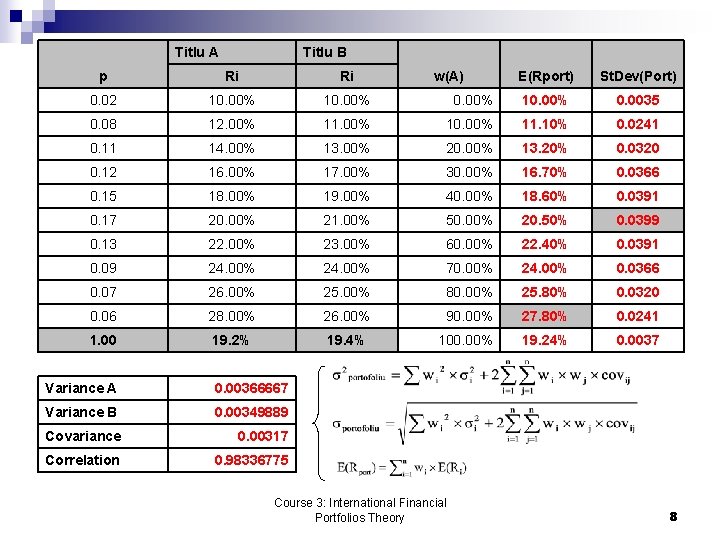
Titlu A Titlu B p Ri Ri 0. 02 10. 00% 0. 08 12. 00% 0. 11 E(Rport) St. Dev(Port) 0. 00% 10. 00% 0. 0035 11. 00% 10. 00% 11. 10% 0. 0241 14. 00% 13. 00% 20. 00% 13. 20% 0. 0320 0. 12 16. 00% 17. 00% 30. 00% 16. 70% 0. 0366 0. 15 18. 00% 19. 00% 40. 00% 18. 60% 0. 0391 0. 17 20. 00% 21. 00% 50. 00% 20. 50% 0. 0399 0. 13 22. 00% 23. 00% 60. 00% 22. 40% 0. 0391 0. 09 24. 00% 70. 00% 24. 00% 0. 0366 0. 07 26. 00% 25. 00% 80. 00% 25. 80% 0. 0320 0. 06 28. 00% 26. 00% 90. 00% 27. 80% 0. 0241 1. 00 19. 2% 19. 4% 100. 00% 19. 24% 0. 0037 Variance A 0. 00366667 Variance B 0. 00349889 Covariance 0. 00317 Correlation 0. 98336775 w(A) Course 3: International Financial Portfolios Theory 8
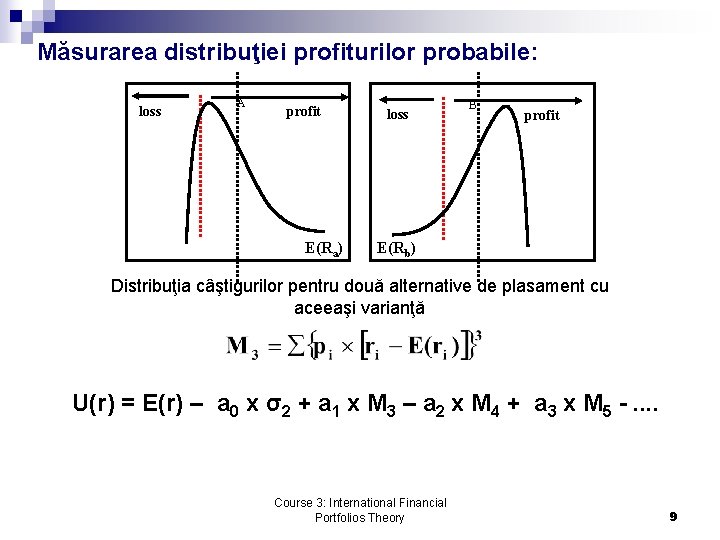
Măsurarea distribuţiei profiturilor probabile: loss A profit E(Ra) loss B profit E(Rb) Distribuţia câştigurilor pentru două alternative de plasament cu aceeaşi varianţă U(r) = E(r) – a 0 x σ2 + a 1 x M 3 – a 2 x M 4 + a 3 x M 5 -. . Course 3: International Financial Portfolios Theory 9
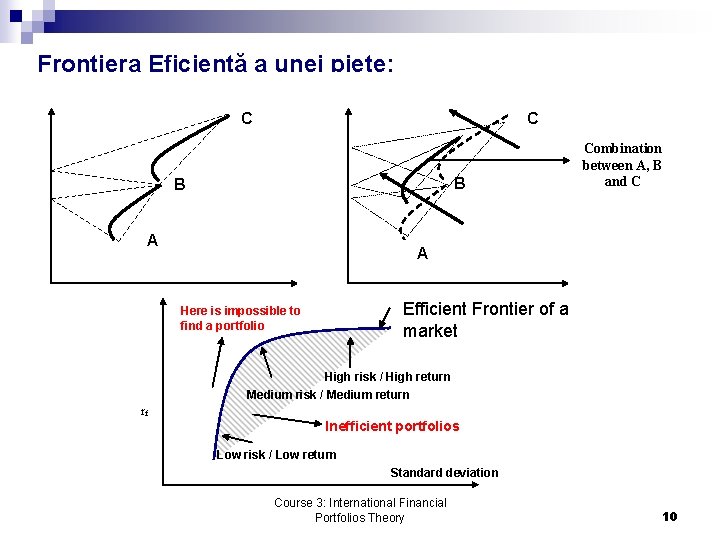
Frontiera Eficientă a unei pieţe: C C B B A Combination between A, B and C A Efficient Frontier of a market Here is impossible to find a portfolio High risk / High return Medium risk / Medium return rf Inefficient portfolios Low risk / Low return Standard deviation Course 3: International Financial Portfolios Theory 10
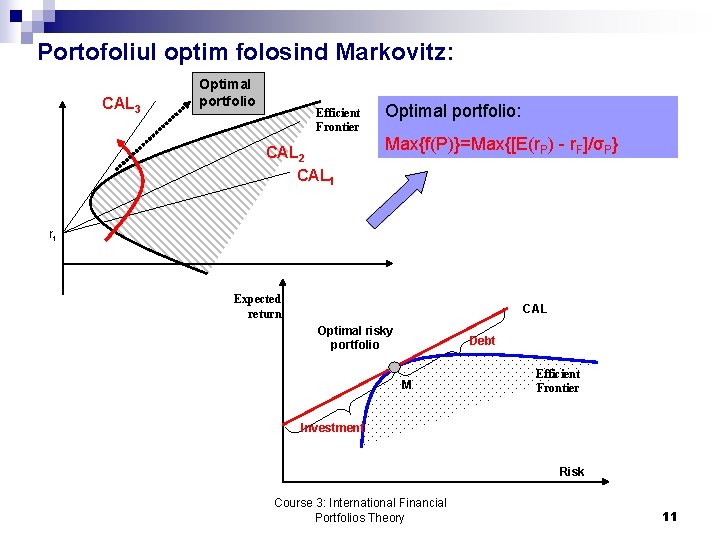
Portofoliul optim folosind Markovitz: CAL 3 Optimal portfolio Efficient Frontier CAL 2 CAL 1 Optimal portfolio: Max{f(P)}=Max{[E(r. P) - r. F]/σP} rf Expected return CAL Optimal risky portfolio Debt M Efficient Frontier Investment Risk Course 3: International Financial Portfolios Theory 11
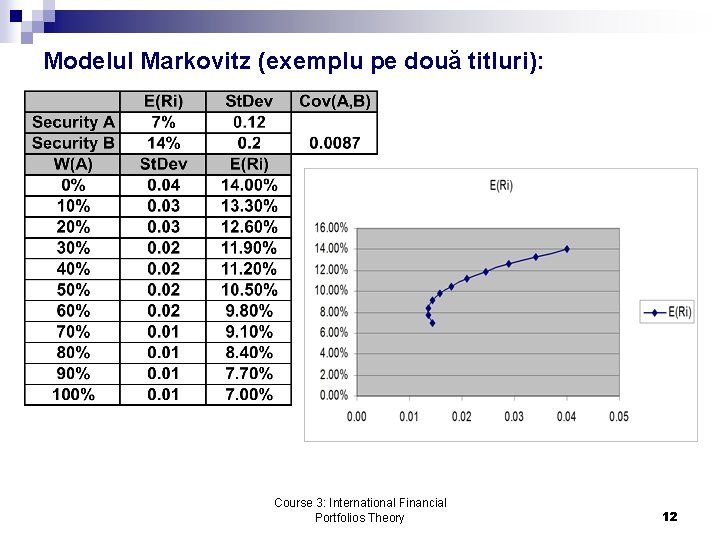
Modelul Markovitz (exemplu pe două titluri): Course 3: International Financial Portfolios Theory 12
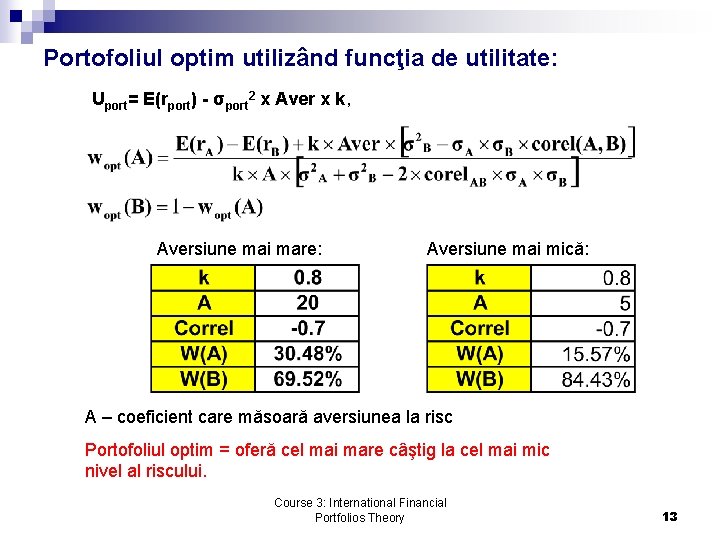
Portofoliul optim utilizând funcţia de utilitate: Uport= E(rport) - σport 2 x Aver x k, Aversiune mai mare: Aversiune mai mică: A – coeficient care măsoară aversiunea la risc Portofoliul optim = oferă cel mai mare câştig la cel mai mic nivel al riscului. Course 3: International Financial Portfolios Theory 13
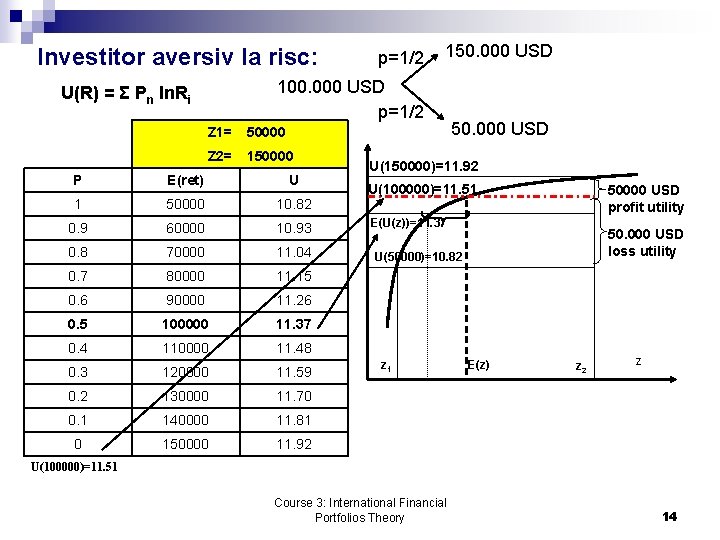
Investitor aversiv la risc: p=1/2 150. 000 USD 100. 000 USD p=1/2 U(R) = Σ Pn ln. Ri Z 1= 50000 Z 2= 150000 P E(ret) U 1 50000 10. 82 0. 9 60000 10. 93 0. 8 70000 11. 04 0. 7 80000 11. 15 0. 6 90000 11. 26 0. 5 100000 11. 37 0. 4 110000 11. 48 0. 3 120000 11. 59 0. 2 130000 11. 70 0. 1 140000 11. 81 0 150000 11. 92 50. 000 USD U(150000)=11. 92 U(100000)=11. 51 50000 USD profit utility E(U(z))=11. 37 50. 000 USD loss utility U(50000)=10. 82 z 1 E(z) z 2 z U(100000)=11. 51 Course 3: International Financial Portfolios Theory 14
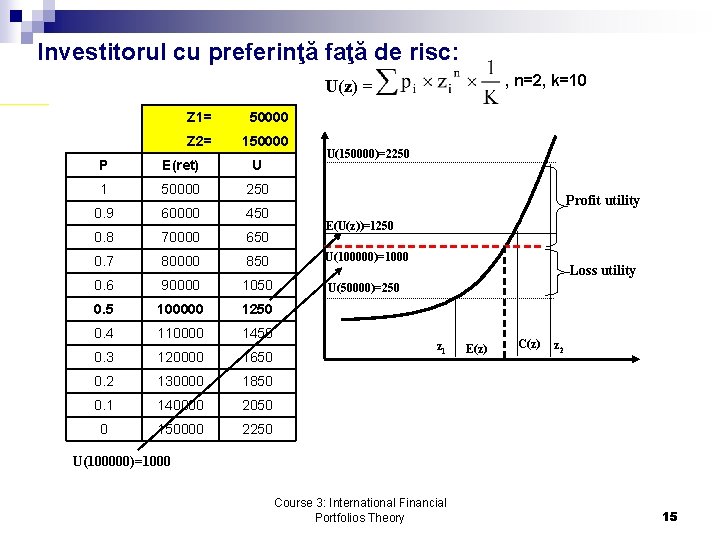
Investitorul cu preferinţă faţă de risc: , n=2, k=10 U(z) = Z 1= 50000 Z 2= 150000 U(150000)=2250 P E(ret) U 1 50000 250 0. 9 60000 450 0. 8 70000 650 0. 7 80000 850 U(100000)=1000 0. 6 90000 1050 U(50000)=250 0. 5 100000 1250 0. 4 110000 1450 0. 3 120000 1650 0. 2 130000 1850 0. 1 140000 2050 0 150000 2250 Profit utility E(U(z))=1250 Loss utility z 1 E(z) C(z) z 2 U(100000)=1000 Course 3: International Financial Portfolios Theory 15
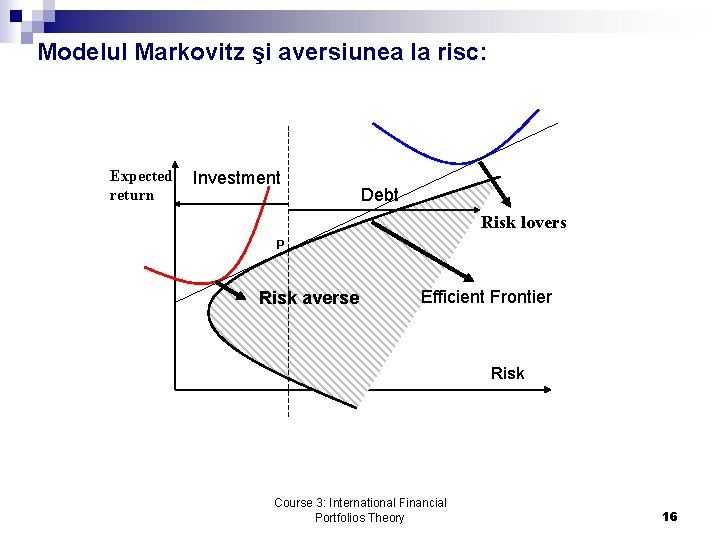
Modelul Markovitz şi aversiunea la risc: Expected return Investment Debt Risk lovers P Risk averse Efficient Frontier Risk Course 3: International Financial Portfolios Theory 16

Concluzii: • Folosind datele istorice putem aloca o serie de probabilităţi unor aşteptări legate de câştigurile viitoare; • Câştigul aşteptat se bazează pe o medie a câştigurilor istorice; • există un singur portofoliu optim pe piaţă; • Modelul Markovitz este mai puţin relevant în cazul portofoliilor financiare internaţionale; • Modelul a îmbunătăţit selecţia titlurilor pe o piaţă; • Portofoliul riscant optim fiind unic = > industria f. de pensii… • Modelul Markovitz ia în calcul aversiunea la risc a investitorilor; Course 3: International Financial Portfolios Theory 17

B. Capital Asset Pricing Model Course 3: International Financial Portfolios Theory 18

CAPM ipotezele de bază: • pe piaţă există un număr mare de investitori (incapacitatea de a influenţa preţurile pieţei); • există un timp limitat de luare a deciziei (comportament “miopic”); • pe piaţă avem intrumente riscante şi instrumente fără risc • pe piaţă nu avem costuri de tranzacţionare şi impozite aplicate tranzacţiilor financiare; • toţi investitorii au un comportament raţional (maximizează randamentele lor) • toţi investitorii analizează alternativele de investiţii în acelaşi mod (randamentele sunt omogene) • portofoliu riscant optim este portofoliul pieţei; • prima de risc = Rm – RFR • măsura riscului unui instrument financiar: coeficientul beta Course 3: International Financial Portfolios Theory 19
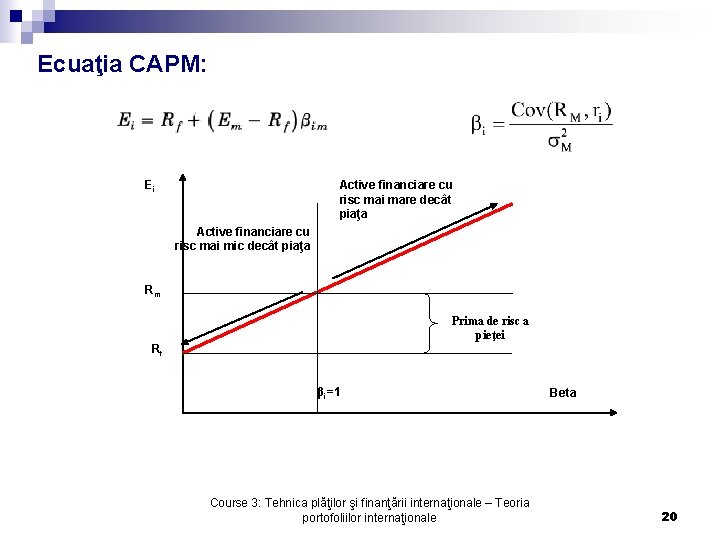
Ecuaţia CAPM: Ei Active financiare cu risc mai mare decât piaţa Active financiare cu risc mai mic decât piaţa Rm Prima de risc a pieţei Rf βi=1 Course 3: Tehnica plăţilor şi finanţării internaţionale – Teoria portofoliilor internaţionale Beta 20

Avantaje şi dezavantaje ale CAPM: • face pentru prima dată distincţia între riscul sistematic şi riscul nesistematic; • CAPM este un model simplu şi uşor de utilizat; • nu există instrumente financiare fără risc; • dificil de obţinut şi de calculat portofoliul pieţei; • piaţa nu este singurul factor determinant al aşteptărilor legate de câştig (dimensiunea companiei, impozitarea); • aproximarea cu indicele pieţei; • CAPM este un model static; • testele de relevanţă ale CAPM nu au confirmat validitatea ipotezele modelului (Roll, Fama & Mac. Beth, Banz, Jensen); • dificultăţi în crearea unui CAPM global; Course 3: International Financial Portfolios Theory 21

C. Teoria arbitrajului Course 3: International Financial Portfolios Theory 22

Ipotezele modelului APT: • modelele factoriale pot explica randamentele financiare; • oportunităţile de arbitraj = portofolii fără investiţii; • oportunităţile de arbitraj apar când este încălcată regula preţului unic • pieţele financiare se caracterizează prin volatilitate ridicată; • echilibrul raţional al pieţei este efectul presiunilor exercitate de existenţa oportunităţilor de arbitraj; • încălcarea principiilor de existenţă condiţiilor de arbitraj este o formă evidentă de iraţionalitate pe piaţă; • modul de valorificare a oportunităţilor de arbitraj nu depind de aversiunea la risc. Course 3: International Financial Portfolios Theory 23

Ecuaţia modelului APT: Risc sistematic Risc nesistematic Factorii de risc: 1. Chen, Ross and Roll APT Model 2. Fama & French APT Model 3. Morgan Stanley APT Model 4. Salomon Smith Barney APT Model Course 3: International Financial Portfolios Theory 24

Chen, Ross and Roll APT Model (original APT): 1. Producţia industrială (reflectă schimbări în aşteptările legate de fluxurile de numerar) 2. Diferenţa de randament între obligaţiunile corporative cu risc scăzut şi cu risc ridicat (schimbări în preferinţa de risc a investitorilor) 3. Diferenţa între dobânta pe TS şi TL (schimbări în preferinţa de timp) 4. Inflaţia neanticipată 5. Inflaţia aşteptată (mai puţin importantă) Modelul APT al lui Fama şi French: 1. Piaţa 2. Dimensiunea companiei 3. Valoarea de piaţă a companiei (Book-to-market factor) Course 3: International Financial Portfolios Theory 25

Morgan Stanley APT Model: • • • Creşterea PIB Dobânda pe termen lung Cursul de schimb (coş valutar Yen, Euro, Pound) Factorul pieţei Indicele preţurilor de consum sau indicele preţurilor pentru bunurile petroliere Salomon Smith Barney APT Model 1. Trendul pieţei 2. Creşterea economică 3. Calitatea creditului 4. Ratele de dobândă 5. Şocurile inflaţioniste 6. Prima la instrumentele sintetice pe rata dobânzii Course 3: International Financial Portfolios Theory 26

Probleme cu APT: • Existenţa oportunităţilor de arbitraj (încălcari frecvente ale regulii preţurilor unice pe pieţe); • Dificultăţi în găsirea factorilor determinanţi pentru randamentele financiare (aceşti factori trebuie să fie necorelaţi între ei şi randamentele aşteptate ale tuturor instrumentelor financiare trebuie să fie sensibili la aceştia) • Unicitatea factorilor de risc; • Aplicarea modelului pe caz real; • Stabilitatea relaţiei între câştigurile aşteptate şi factorii de risc pe o perioadă mai mare de timp; • Independenţa între factorii de risc nu se menţine pe perioade determinate de timp; • Modificări în ceea ce priveşte sensibilitatea randamentelor aşteptate la factorii de risc. Course 3: International Financial Portfolios Theory 27

Concluzii finale: • Cele mai importante resurse financiare se obţin de pe pieţele internaţionale de capital prin emisiunea de acţiuni şi obligaţiuni; • Atunci când o companie ia decizia de a emite titluri pe pieţele financiare este important ca ea să înţeleagă comportamentul investiţional; • Decizia de plasament se bazează pe analiza randamentelor şi riscurilor financiare la care se expun investitorii; • Există diferite teorii cu privire la portofoliile financiare: • Markovitz: media pentru aşteptările de câştig şi dispersia pentru risc • CAPM: relaţie liniară între câştigurile aşteptate şi riscul acestora măsurat printr-un indicator specific – beta; • APT: o relaţie liniară între un număr mult mai mare de factori independenţi şi necorelaţi; • investitorii au o funcţie de utilitate care explică comportamentul lor; • există diferite atitudini legate de risc (aversiune, preferinţă, indiferenţă); • pe piaţă există oportunităţi de arbitraj. 28
- Slides: 28