AC Current n n An AC circuit consists

AC Current n n An AC circuit consists of a combination of circuit elements and an AC generator or source The output of an AC generator is sinusoidal and varies with time according to the following equation q V = V 0 sin 2 ƒt n n n V is the instantaneous voltage V 0 is the maximum voltage of the generator ƒ is the frequency at which the voltage changes, in Hz

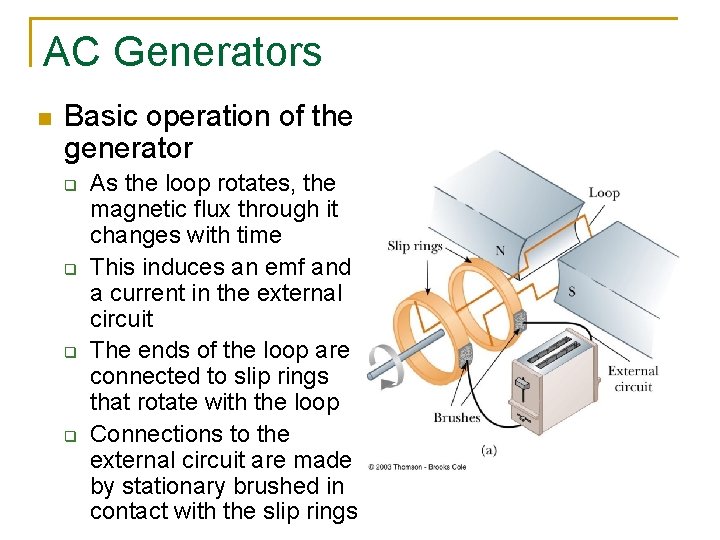
AC Generators n Basic operation of the generator q q As the loop rotates, the magnetic flux through it changes with time This induces an emf and a current in the external circuit The ends of the loop are connected to slip rings that rotate with the loop Connections to the external circuit are made by stationary brushed in contact with the slip rings

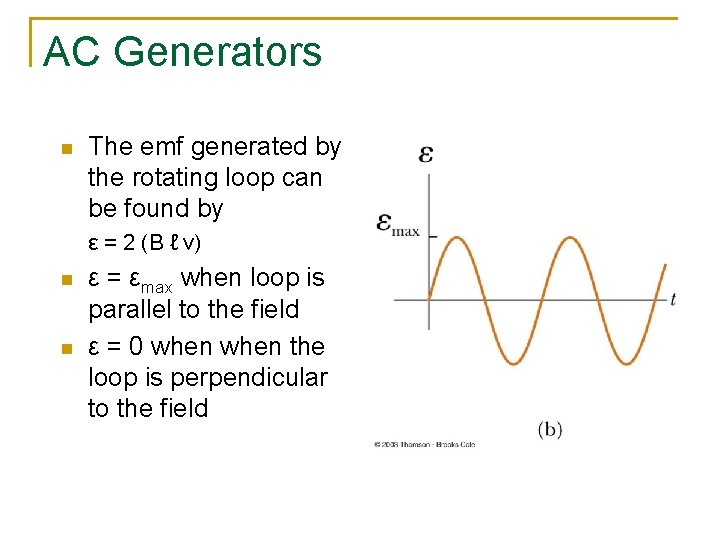
AC Generators n The emf generated by the rotating loop can be found by ε = 2 (B ℓ v) n n ε = εmax when loop is parallel to the field ε = 0 when the loop is perpendicular to the field

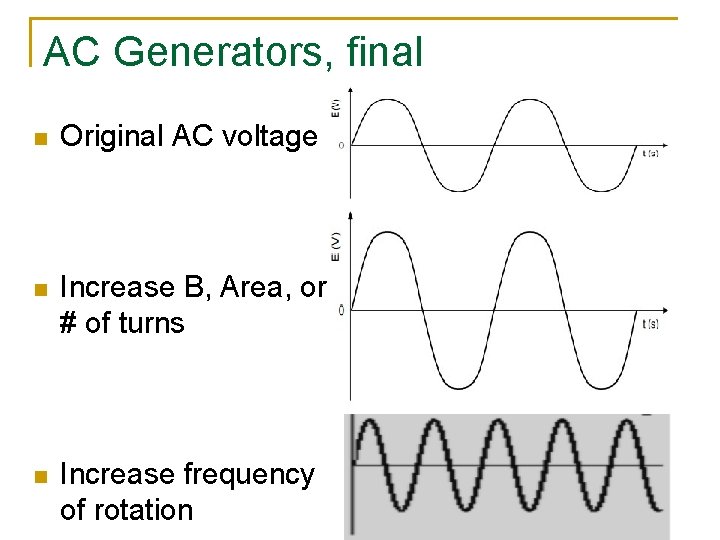
AC Generators, final n Original AC voltage n Increase B, Area, or # of turns n Increase frequency of rotation

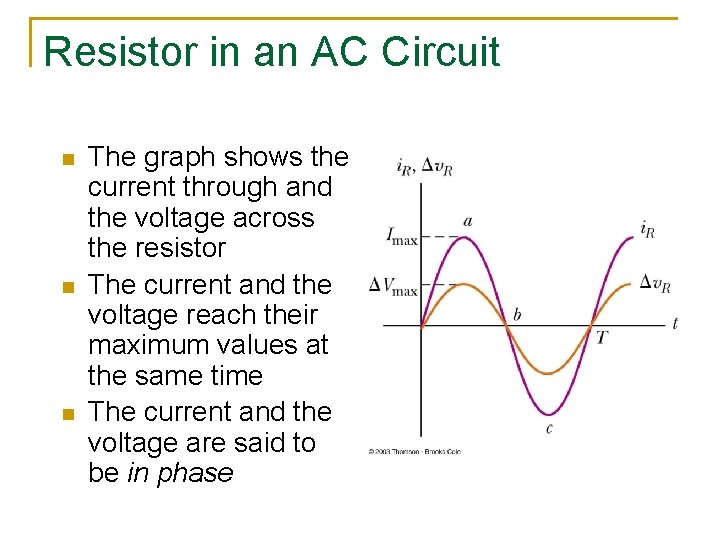
Resistor in an AC Circuit n n n The graph shows the current through and the voltage across the resistor The current and the voltage reach their maximum values at the same time The current and the voltage are said to be in phase

rms Current and Voltage n The rms current is the direct current that would dissipate the same amount of energy in a resistor as is actually dissipated by the AC current Irms n = I Io = peak or max current o 2 Alternating voltages can also be discussed in terms of rms values V rms = V 0 2 Vo = peak voltage

Ohm’s Law in an AC Circuit n rms values will be used when discussing AC currents and voltages q n AC ammeters and voltmeters are designed to read rms values Ohm’s Law for a resistor, R, in an AC circuit q ΔVrms = Irms R

Example An AC voltage source has a peak output of 200 V. If the source is connected to a 100 W resistor, find the rms current. V rms = I rms = V 0 2 V rms R What is the max current? = 200 V 2 = 141 V / 100 W = 1. 41 A Irms = I o 2 1. 41 A = I o 2 Io = 2 A

Transformers

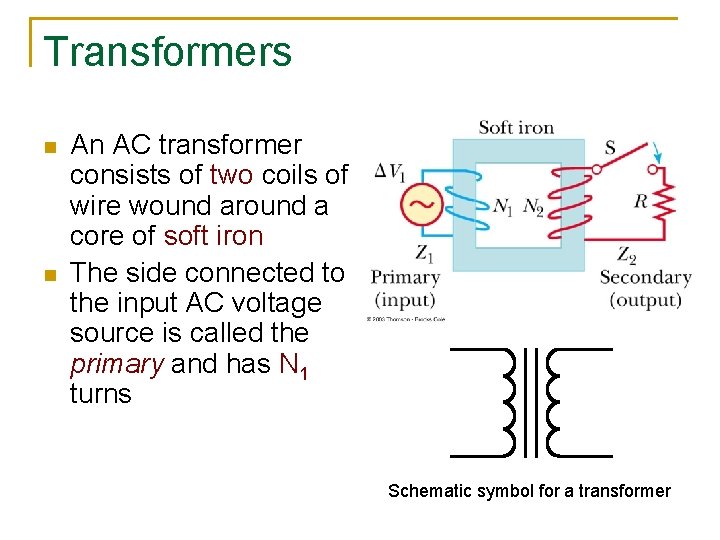
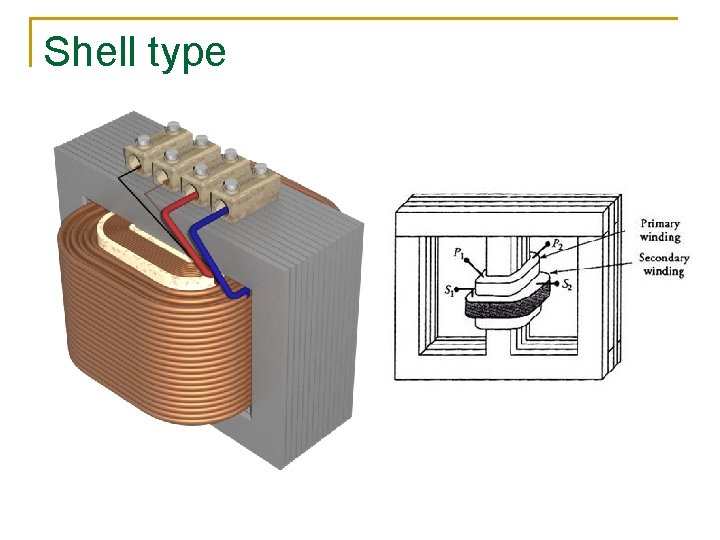
Transformers n n An AC transformer consists of two coils of wire wound around a core of soft iron The side connected to the input AC voltage source is called the primary and has N 1 turns Schematic symbol for a transformer

Shell type

Transformers, 2 n The other side, called the secondary, is connected to a resistor and has N 2 turns n Current passing through the primary coil induces a magnetic field (magnetic flux) in the iron core. The magnetic flux is transmitted to the other side and induces a voltage in the secondary coil.

Transformers, 3 n The voltages are related by Where: Vp = Primary coil voltage Vs = Secondary coil voltage Np = # of turns of wire in the Primary coil Ns = # of turns of wire in the Secondary coil

Transformers, 4 n. When Ns > Np, the transformer is referred to as a step up transformer (more voltage out) n. When Np > Ns, the transformer is referred to as a step down transformer (less voltage out) *This works because there is a direct relationship between the # of turns and the induced voltage

Transformer, 5 n The power input into the primary equals the power output at the secondary q I 1ΔV 1 = I 2ΔV 2 n q You don’t get something for nothing (conservation of energy) This assumes an ideal transformer n In real transformers, power efficiencies typically range from 90% to 99%

Electrical Power Transmission n When transmitting electric power over long distances it is most economical to use high voltage and low current q n Minimizes I 2 R power losses (P = VI = I 2 R) In practice, voltage is stepped up to about 230, 000 V at the generating station and stepped down to 20 000 V at the distribution station and finally to 120 V at the customer’s utility pole