AC Circuits Energy Unit AC Circuits Study School

AC Circuits Energy Unit AC Circuits Study: School of Electrical, Electronic and Computer Engineering G. Rizzoni, J. Kearnes, 6 th Ed. Principles and Applications of Electrical Engineering Chapter 4: AC Network Analysis

Key Concepts: Fundamentals and Techniques (1) • What is a Capacitor? – A capacitor (denoted by C) is a passive element designed to store energy in its electric field – Its current-voltage relationship is described by a differential equation: i = C (dv/dt). The current through a capacitor is proportional to the rate of change in voltage across the capacitor – No current through capacitor if voltage is static (acts like open-circuit) Need an alternating or sinusoidal voltage across capacitor • What is an Inductor? – An inductor (denoted by L) is a passive element designed to store energy in its magnetic field. – Its voltage–current relationship is described by a differential equation: v = L (di/dt). The voltage across an inductor is proportional to the rate of change in current through the inductor – No voltage across the inductor if current is static (acts like short-circuit) Need an alternating or sinusoidal current through inductor 2

Key Concepts: Fundamentals and Techniques (1)(1) • Phasor Analysis / Impedance Model / AC Circuits – How to analyse circuits excited by harmonic / sinusoidal excitation using complex numbers phasors – Converting between time-domain and phasor-domain – How L and C components behave (the impedance model) – Using standard analysis (KCL, KVL, impedance model) for the steady-state response of circuits excited by sinusoids, but with complex equations • Impedance Combination – How to combine multiple series-connected/parallel-connected impedances – Implementing voltage-division/current-division in series/parallel ac circuits • Wye-delta and delta-to-wye transformations for complex impedances – The wye-delta and delta-to-wye transformations that we applied to resistive circuits are also valid for impedances. 3

Capacitors and Inductors An electrical element is defined by its relation between v and i. This is called a constitutive relation. In general, we write v = f(i) or i = g(v) i + v – For a resistor, v = i * R The constitutive relation of a resistor has no dependence upon time. 4

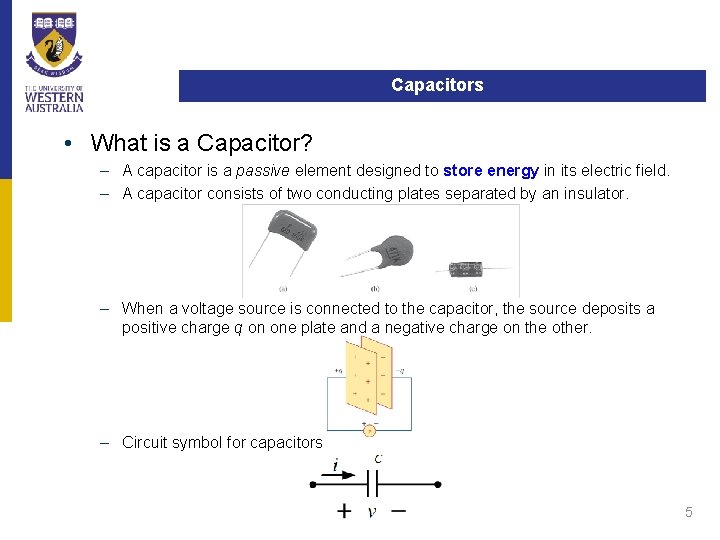
Capacitors • What is a Capacitor? – A capacitor is a passive element designed to store energy in its electric field. – A capacitor consists of two conducting plates separated by an insulator. – When a voltage source is connected to the capacitor, the source deposits a positive charge q on one plate and a negative charge on the other. – Circuit symbol for capacitors 5

Capacitors • 6

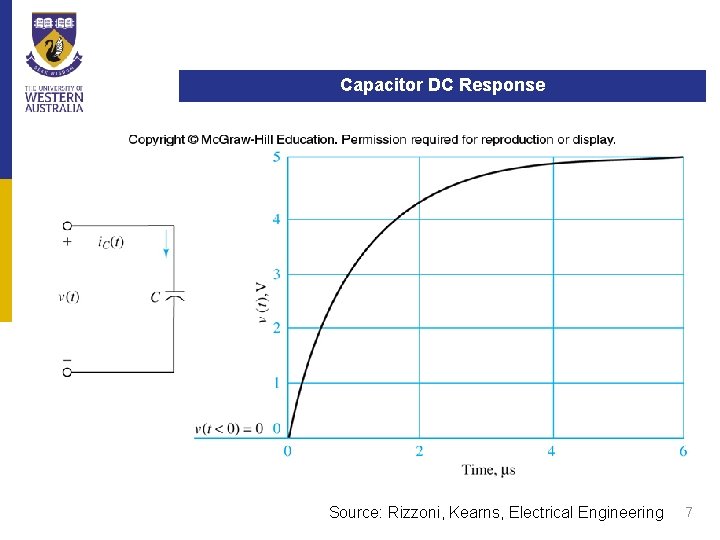
Capacitors Capacitor DC Response Source: Rizzoni, Kearns, Electrical Engineering 7

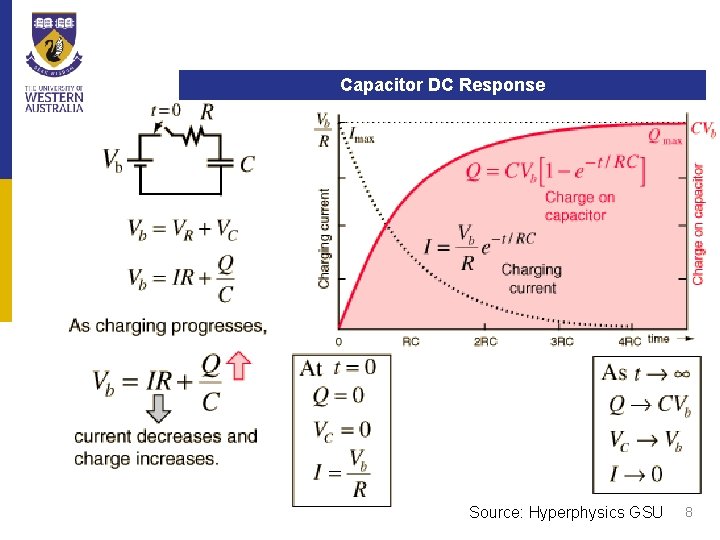
Capacitor. Inductors DC Response Source: Hyperphysics GSU 8

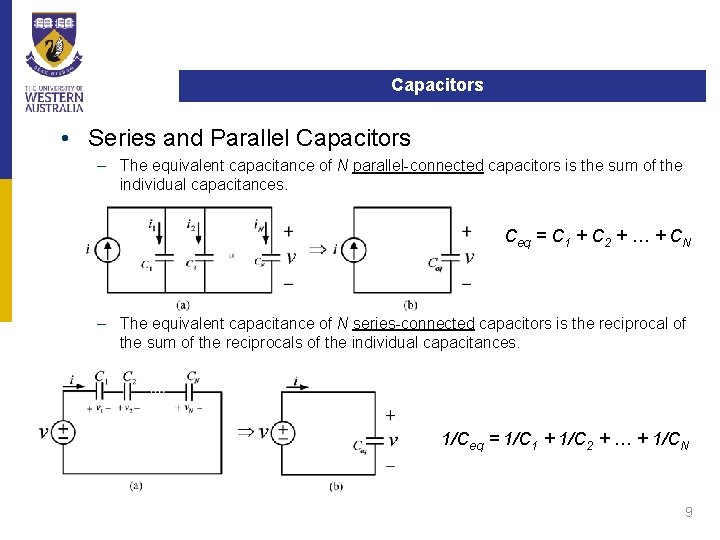
Capacitors • Series and Parallel Capacitors – The equivalent capacitance of N parallel-connected capacitors is the sum of the individual capacitances. Ceq = C 1 + C 2 + … + CN – The equivalent capacitance of N series-connected capacitors is the reciprocal of the sum of the reciprocals of the individual capacitances. 1/Ceq = 1/C 1 + 1/C 2 + … + 1/CN 9

Inductors • What is an Inductor? – An inductor is a passive element designed to store energy in its magnetic field. – An inductor consists of a coil of conducting wire. – Inductance (L) of an inductor is the property that an inductor exhibits opposition to the change of current flowing through it, measured in henrys (H). – Circuit symbol for inductor 10

Inductors • 11

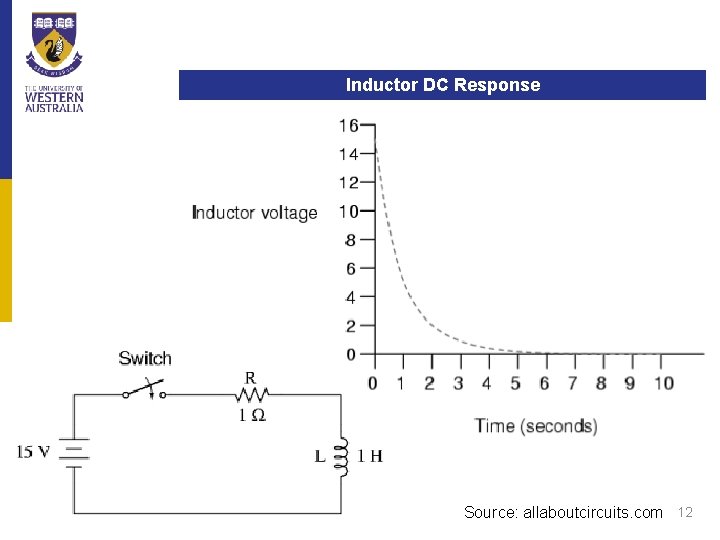
Inductors DC Response Source: allaboutcircuits. com 12

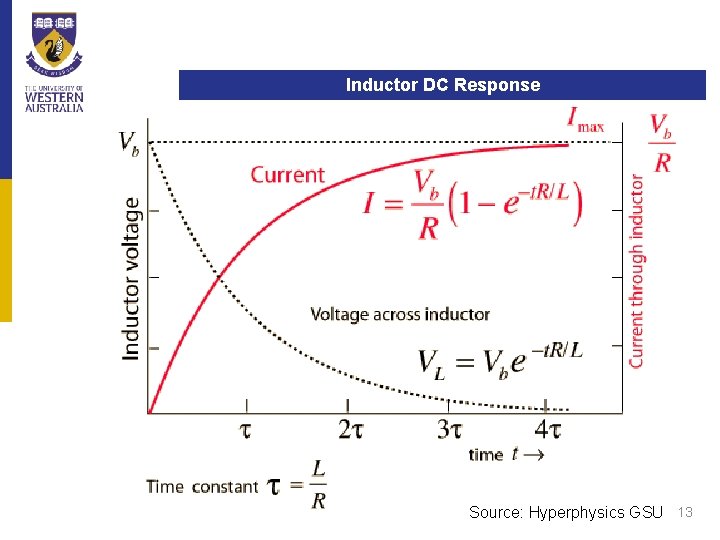
Inductors DC Response Source: Hyperphysics GSU 13

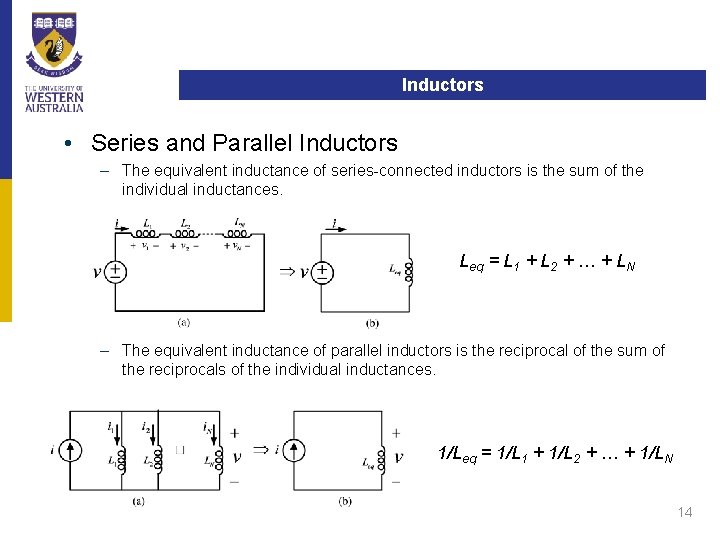
Inductors • Series and Parallel Inductors – The equivalent inductance of series-connected inductors is the sum of the individual inductances. Leq = L 1 + L 2 + … + LN – The equivalent inductance of parallel inductors is the reciprocal of the sum of the reciprocals of the individual inductances. 1/Leq = 1/L 1 + 1/L 2 + … + 1/LN 14

Review Inductors Source: Rizzoni, Kearns, Electrical Engineering 15

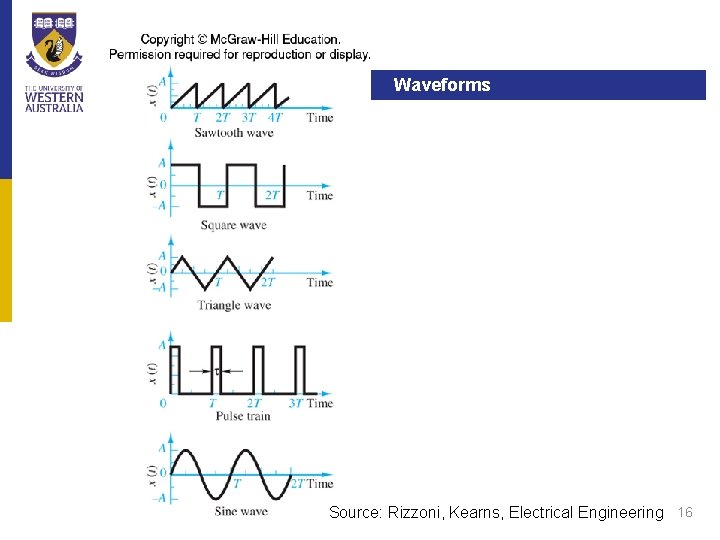
Waveforms Inductors Source: Rizzoni, Kearns, Electrical Engineering 16

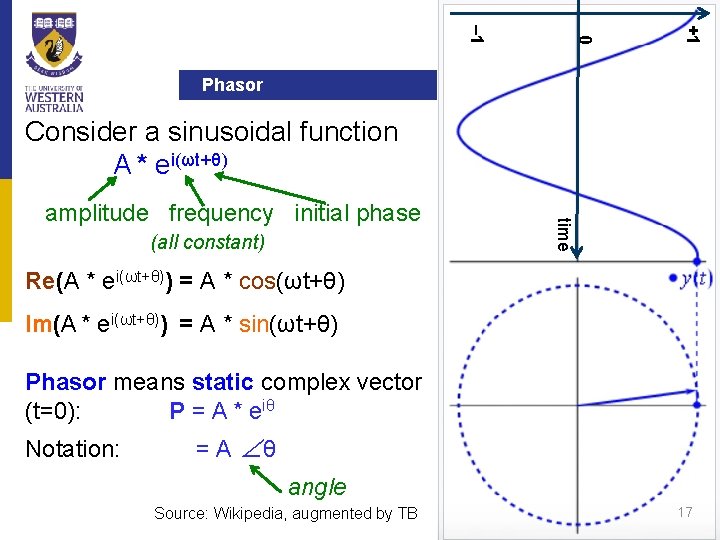
+1 0 – 1 Phasor Inductors Consider a sinusoidal function A * ei(ωt+θ) (all constant) time amplitude frequency initial phase Re(A * ei(ωt+θ)) = A * cos(ωt+θ) Im(A * ei(ωt+θ)) = A * sin(ωt+θ) Phasor means static complex vector (t=0): P = A * eiθ Notation: = A ∠θ angle Source: Wikipedia, augmented by TB 17

Sinusoidal Analysis and Phasors Consider v(t) = Vm * cos(wt +f) Then v(t) = Re (Vm * ej(wt +f)) } = Re (Vm * ejf * ejwt) phasor V = Vm * ejf = Vm ∠f of sinusoid v(t) with frequency w = Re (V * ejwt ) 18

Sinusoidal Analysis and Phasors Some handy relationships: Better: θ = atan 2(X, R) Phasors are complex numbers study Polar/Cartesian representations of complex numbers and how to add/multiply 19

Phasors and Impedance Models We define impedance as: Z = V / I and admittance as: Y=I/V We will write i(t) = Im * cos(wt +F) in phasor form I = Im∠F Similarly v(t) = Vm * cos(wt +F) in phasor form V = Vm∠F Node to Datum analysis and Parallel/Series reductions can be applied to circuits where resistance/conductance is replaced by impedance/admittance. These will be complex equations! 20

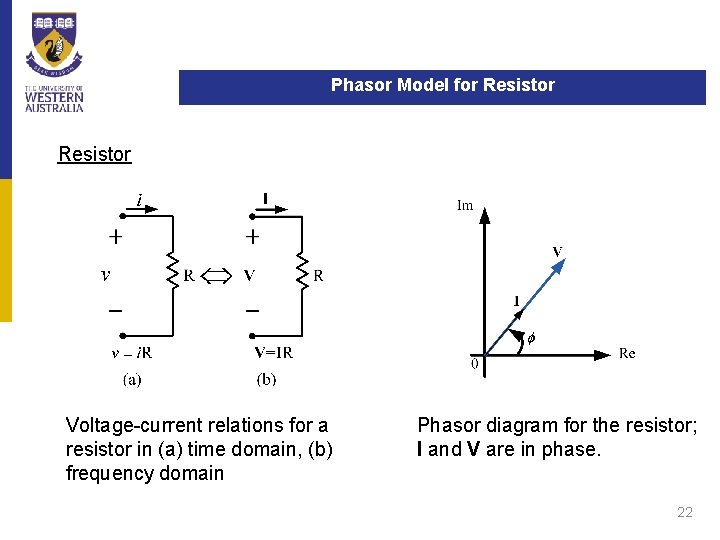
Phasors and Impedance Models Resistor v(t) = R * i(t) = R * Im * cos(wt + ϕ) The phasor form for the voltage is then (t=0): V = R * Im ∠ϕ = R * I Hence we have: Z = R ∠ 0 o Y = (1/R) ∠ 0 o and 21

Phasor Model for Resistor Voltage-current relations for a resistor in (a) time domain, (b) frequency domain Phasor diagram for the resistor; I and V are in phase. 22

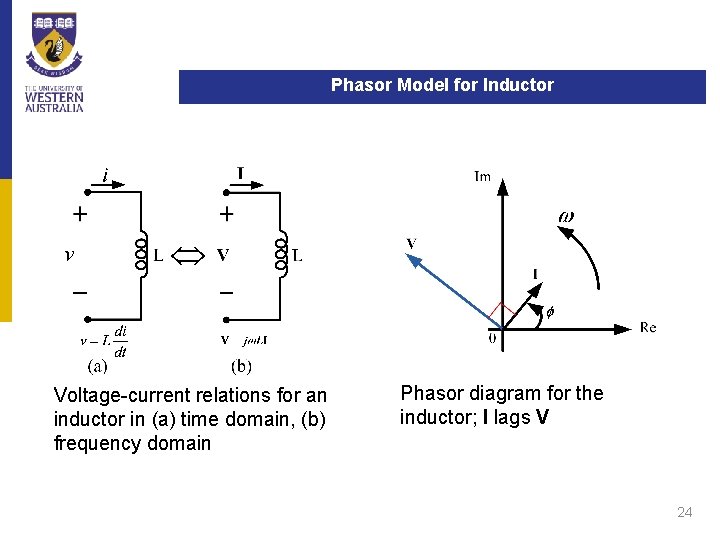
Phasor Model for Inductor Remember: i(t) = Im * cos(wt + ϕ) (t=0) ∠��j 90° 23

Phasor Model for Inductor Voltage-current relations for an inductor in (a) time domain, (b) frequency domain Phasor diagram for the inductor; I lags V 24

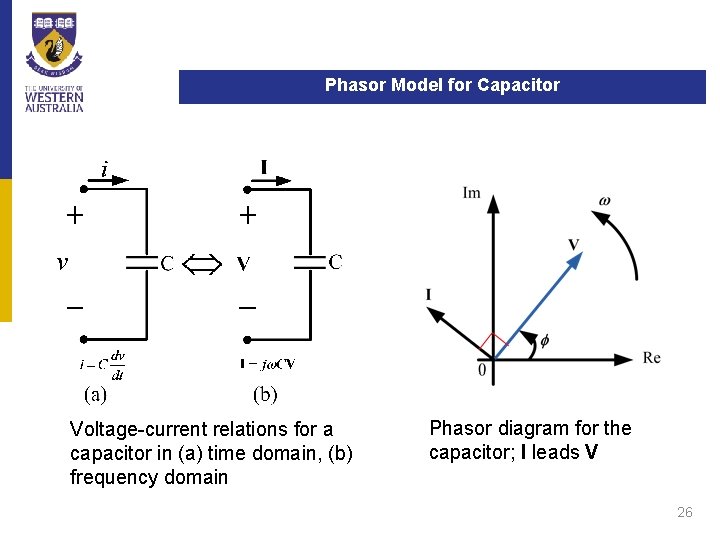
Phasor Model for Capacitor Remember: v(t) = Vm * cos(wt +F) ∠��j 90° 25

Phasor Model for Capacitor Voltage-current relations for a capacitor in (a) time domain, (b) frequency domain Phasor diagram for the capacitor; I leads V 26

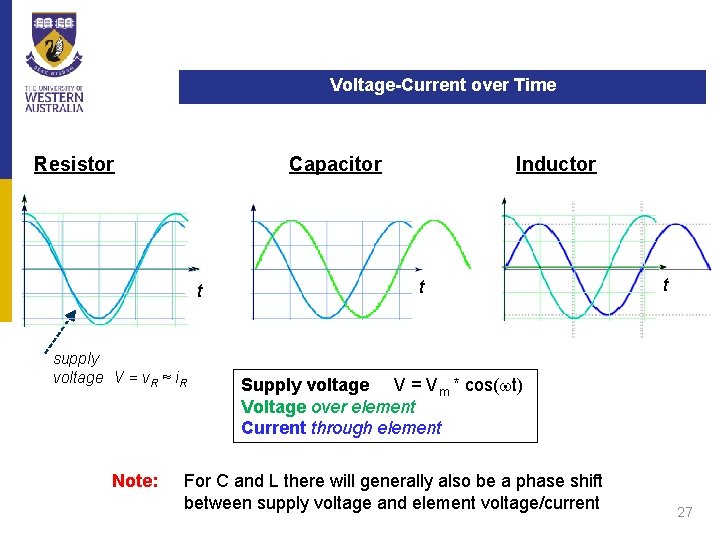
Voltage-Current over Time Resistor Capacitor t supply voltage V = v. R ≈ i. R Note: Inductor t t Supply voltage V = Vm * cos(wt) Voltage over element Current through element For C and L there will generally also be a phase shift between supply voltage and element voltage/current 27

Phasor Relationships for Circuit Elements Summary of voltage-current/current-voltage relationships for resistor, inductor and capacitor Element Time domain Frequency domain Resistor R v=R*i V=R*I Inductor L v = L * di/dt V = jωL * I Capacitor C i = C * dv/dt I = jωC * V 28

Impedance and Admittance 29

Impedance and Admittance • The admittance Y of an element (or a circuit) is the ratio of the phasor current through it to the phasor voltage across it. Equivalently, the admittance is the reciprocal of impedance, measured in siemens (S = 1/W). Y=1/Z = I/V • As a complex quantity, we may write Y as Y = G + j. B where G = Re(Y) is called the conductance and B = Im(Y) is called the susceptance. 30

REVIEWComplex. Numbers Source: Wikipedia 31

REVIEWComplex. Numbers Addition (a+bi) + (c+di) = (a+c) + (b+d)*i Multiplication (a+bi) * (c+di) = (ac–bd) + (bc+ad)*i Conjugate z’ = Re(z) – Im(z)*i Note i 2 = i * i = – 1 1/i = i/i 2 = –i Source: Wikipedia 32

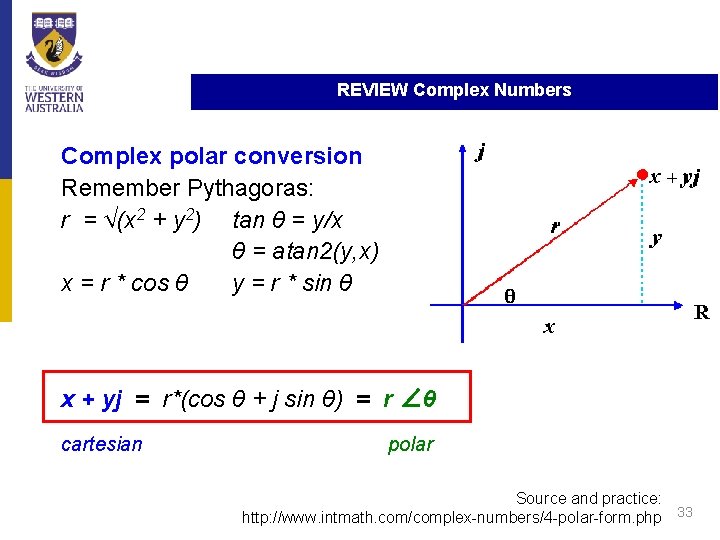
REVIEW Complex Numbers Complex polar conversion Remember Pythagoras: r = √(x 2 + y 2) tan θ = y/x θ = atan 2(y, x) x = r * cos θ y = r * sin θ x + yj = r*(cos θ + j sin θ) = r ∠θ cartesian polar Source and practice: http: //www. intmath. com/complex-numbers/4 -polar-form. php 33

Phasor Arithmetic Better: ϕ = atan 2(B, A) https: //en. wikibooks. org/wiki/Circuit_Theory/Phasor_Arithmetic 34

Phasor Arithmetic https: //en. wikibooks. org/wiki/Circuit_Theory/Phasor_Arithmetic 35

Phasor Arithmetic Multiplication Division https: //en. wikibooks. org/wiki/Circuit_Theory/Phasor_Arithmetic . 36

Phasor Arithmetic Inversion Property Complex Conjugate. https: //en. wikibooks. org/wiki/Circuit_Theory/Phasor_Arithmetic 37

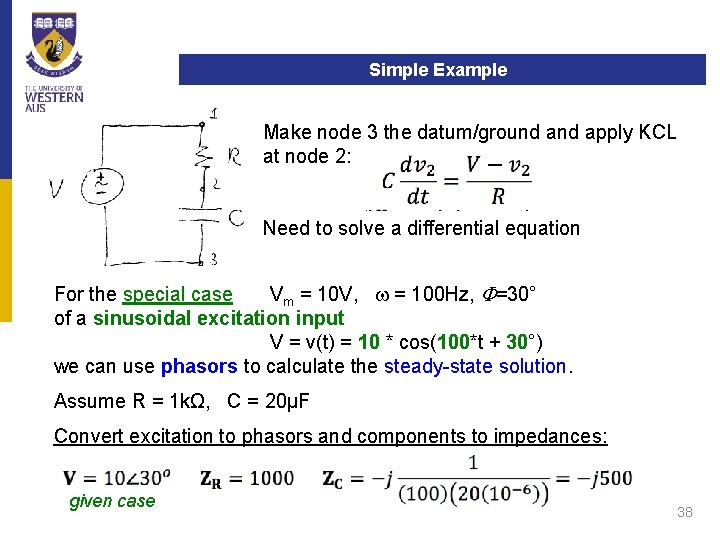
Simple Example Make node 3 the datum/ground apply KCL at node 2: Need to solve a differential equation For the special case Vm = 10 V, w = 100 Hz, F=30° of a sinusoidal excitation input V = v(t) = 10 * cos(100*t + 30°) we can use phasors to calculate the steady-state solution. Assume R = 1 kΩ, C = 20μF Convert excitation to phasors and components to impedances: given case 38

Simple Example Let’s calculate the current. Same techniques as with resistive circuits except that you now use complex numbers 39

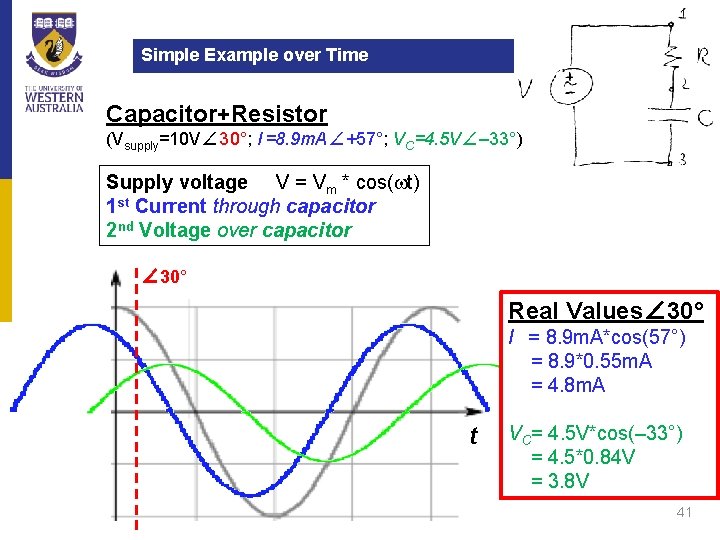
Simple Example We have I = 8. 9 m. A∠ 57° (for case F=30°) Convert phasor solution back to time domain (w=100 Hz) i(t) = 8. 9 m. A * cos(100*t + 57°) Voltage across the capacitor VC = ZC * I = –j*0. 5 kΩ * 8. 9 m. A∠ 57° = 0. 5 kΩ∠– 90° * 8. 9 m. A∠ 57° = 4. 5 V ∠– 33° Note: 90° phase shift! Convert back to time domain vc(t) = 4. 5 V * cos(100 t – 33°) Voltage across resistor VR = ZR * I = 1 kΩ∠ 0° * 8. 9 m. A∠ 57° = 8. 9 V∠ 57° Note: VC + VR = Vsupply 40

Simple Example over Time Capacitor+Resistor (Vsupply=10 V∠ 30°; I =8. 9 m. A∠+57°; VC=4. 5 V∠– 33°) Supply voltage V = Vm * cos(wt) 1 st Current through capacitor 2 nd Voltage over capacitor ∠ 30° Real Values∠ 30° I = 8. 9 m. A*cos(57°) = 8. 9*0. 55 m. A = 4. 8 m. A t VC= 4. 5 V*cos(– 33°) = 4. 5*0. 84 V = 3. 8 V 41

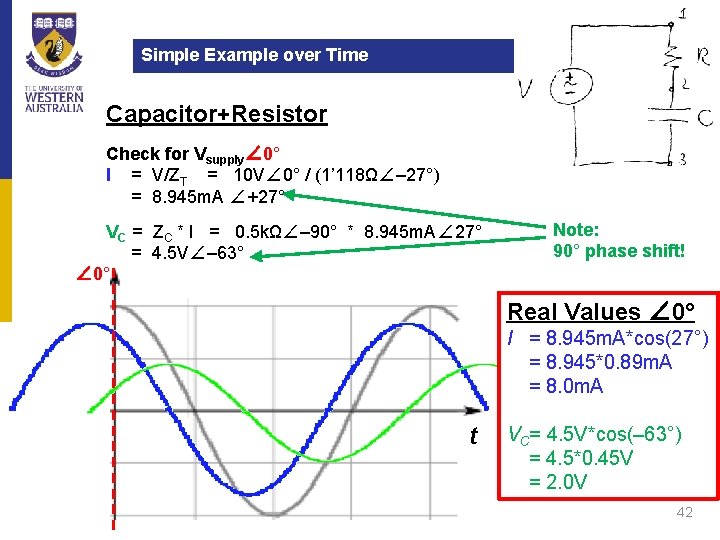
Simple Example over Time Capacitor+Resistor Check for Vsupply∠ 0° I = V/ZT = 10 V∠ 0° / (1’ 118Ω∠– 27°) = 8. 945 m. A ∠+27° VC = ZC * I = 0. 5 kΩ∠– 90° * 8. 945 m. A∠ 27° = 4. 5 V∠– 63° ∠ 0° Note: 90° phase shift! Real Values ∠ 0° I = 8. 945 m. A*cos(27°) = 8. 945*0. 89 m. A = 8. 0 m. A t VC= 4. 5 V*cos(– 63°) = 4. 5*0. 45 V = 2. 0 V 42

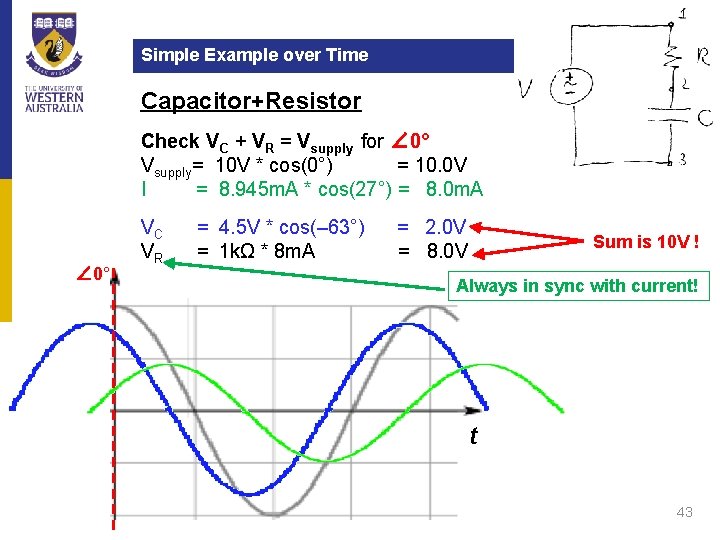
Simple Example over Time Capacitor+Resistor Check VC + VR = Vsupply for ∠ 0° Vsupply= 10 V * cos(0°) = 10. 0 V I = 8. 945 m. A * cos(27°) = 8. 0 m. A ∠ 0° VC VR = 4. 5 V * cos(– 63°) = 1 kΩ * 8 m. A = 2. 0 V = 8. 0 V Sum is 10 V ! Always in sync with current! t 43

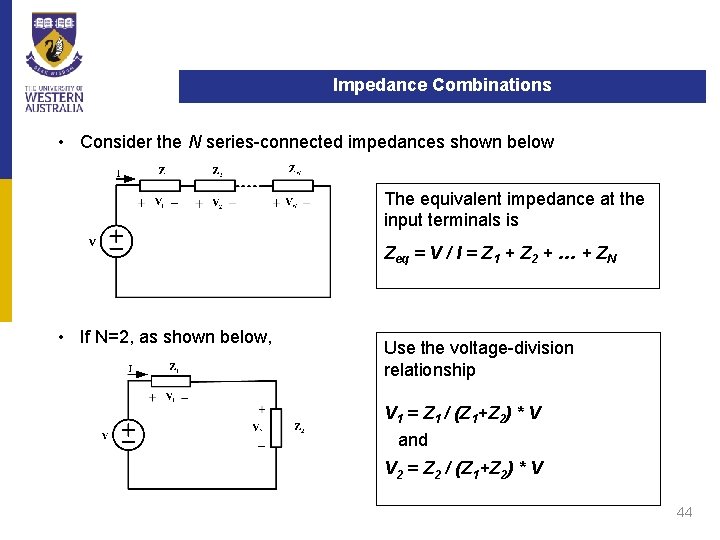
Impedance Combinations • Consider the N series-connected impedances shown below The equivalent impedance at the input terminals is Zeq = V / I = Z 1 + Z 2 + … + ZN • If N=2, as shown below, Use the voltage-division relationship V 1 = Z 1 / (Z 1+Z 2) * V and V 2 = Z 2 / (Z 1+Z 2) * V 44

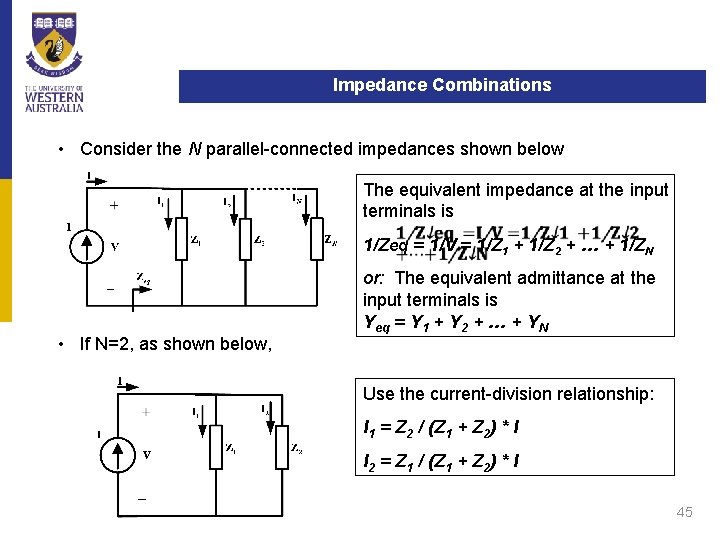
Impedance Combinations • Consider the N parallel-connected impedances shown below The equivalent impedance at the input terminals is 1/Zeq = 1/V = 1/Z 1 + 1/Z 2 + … + 1/ZN • If N=2, as shown below, or: The equivalent admittance at the input terminals is Yeq = Y 1 + Y 2 + … + YN Use the current-division relationship: I 1 = Z 2 / (Z 1 + Z 2) * I I 2 = Z 1 / (Z 1 + Z 2) * I 45

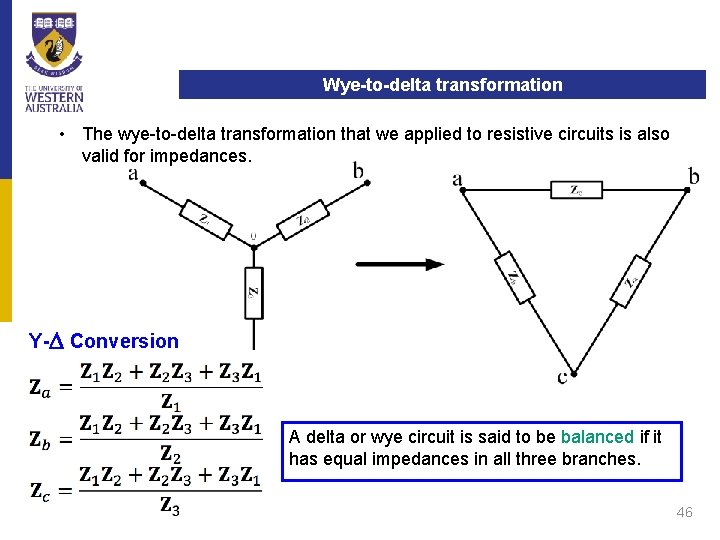
Wye-to-delta transformation • The wye-to-delta transformation that we applied to resistive circuits is also valid for impedances. Y-D Conversion A delta or wye circuit is said to be balanced if it has equal impedances in all three branches. 46

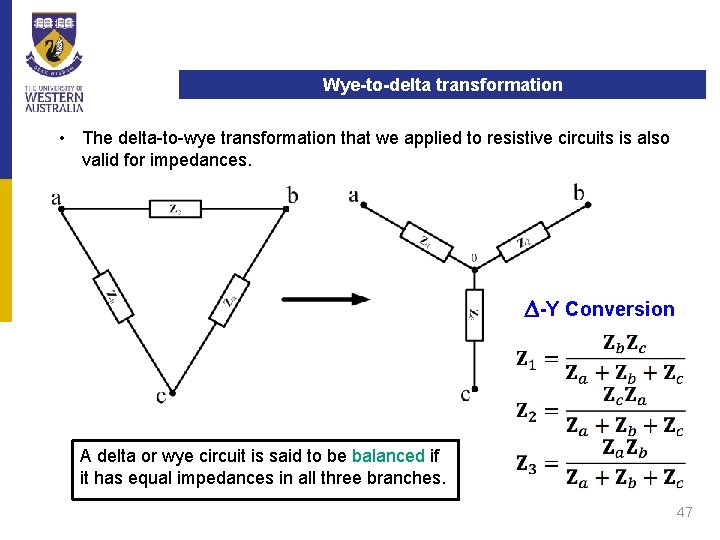
Wye-to-delta Delta-to-wyetransformation • The delta-to-wye transformation that we applied to resistive circuits is also valid for impedances. D-Y Conversion A delta or wye circuit is said to be balanced if it has equal impedances in all three branches. 47