Abstraction of ManMade Shapes Ravish Mehra 1 2

Abstraction of Man-Made Shapes Ravish Mehra 1, 2, Qingnan Zhou 1, Jeremy Long 4, Alla Sheffer 1, Amy Gooch 4, Niloy J. Mitra 2, 3 1 Univ. of British Columbia 2 IIT Abstraction of Man-Made Shapes Delhi 3 KAUST 4 Univ. of Victoria

Human Perception Abstraction of Man-Made Shapes

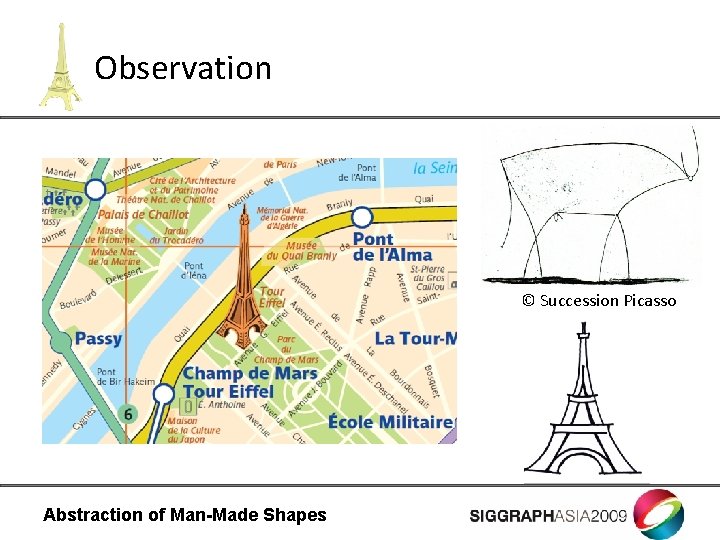
Observation © Succession Picasso Abstraction of Man-Made Shapes

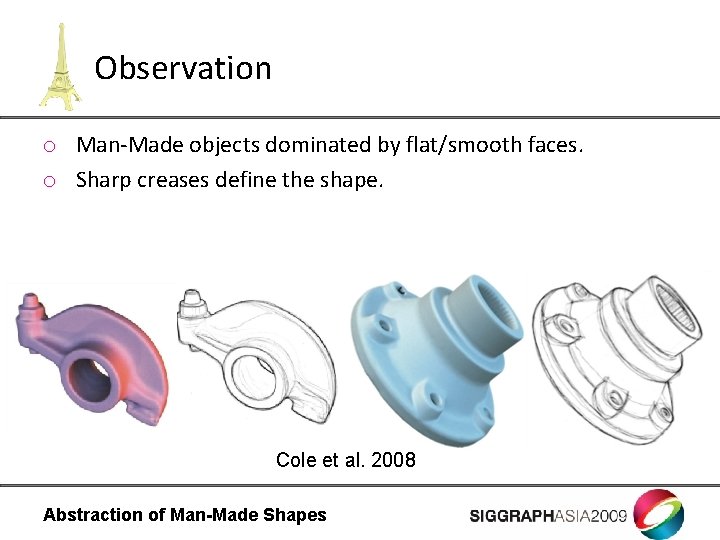
Observation o Man-Made objects dominated by flat/smooth faces. o Sharp creases define the shape. Cole et al. 2008 Abstraction of Man-Made Shapes

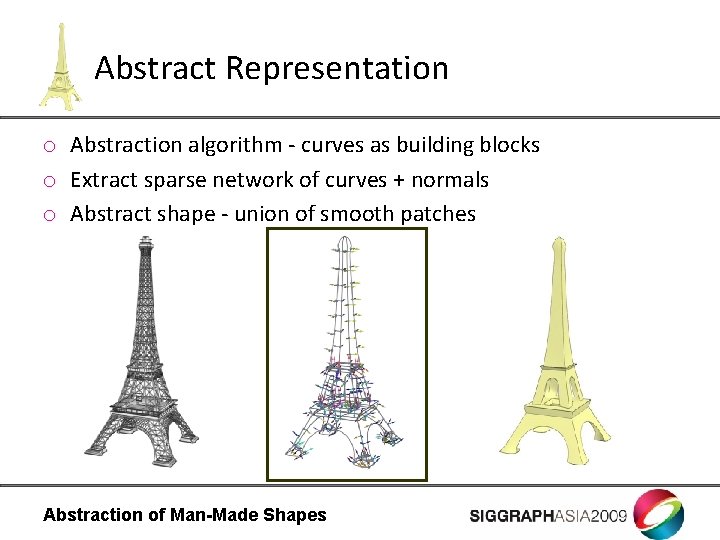
Abstract Representation o Abstraction algorithm - curves as building blocks o Extract sparse network of curves + normals o Abstract shape - union of smooth patches Abstraction of Man-Made Shapes

Related Works o Curve based NPR • Suggestive contours [De. Carlo et al. 2003] • Apparent ridges [Judd et al. 2007] o Curve based surface modeling • Wires [Singh et al. 1998] • Fiber Mesh [Nealen et al. 2007] • i. Wires [Gal et al. 2009] o Vector representation • Diffusion Curves [Orzan et al. 2008] Abstraction of Man-Made Shapes

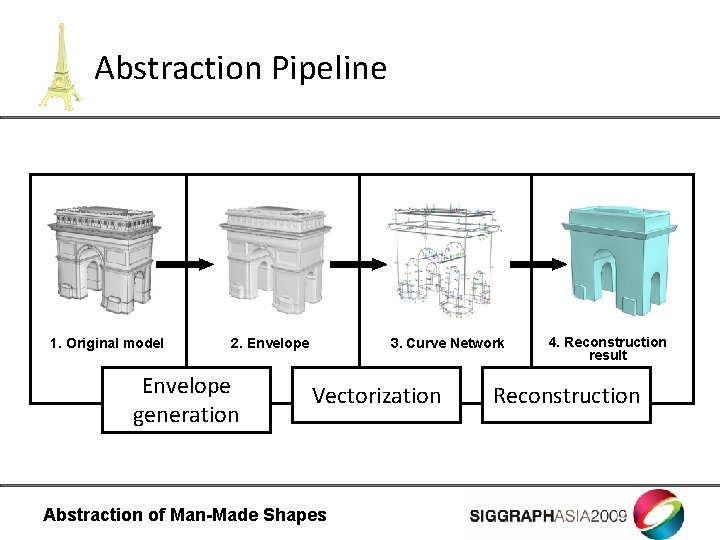
Abstraction Pipeline 1. Original model 2. Envelope generation 3. Curve Network Vectorization Abstraction of Man-Made Shapes 4. Reconstruction result Reconstruction

Challenge o Input contains multiple self-intersecting components. o Can even be a polygon soup. Abstraction of Man-Made Shapes

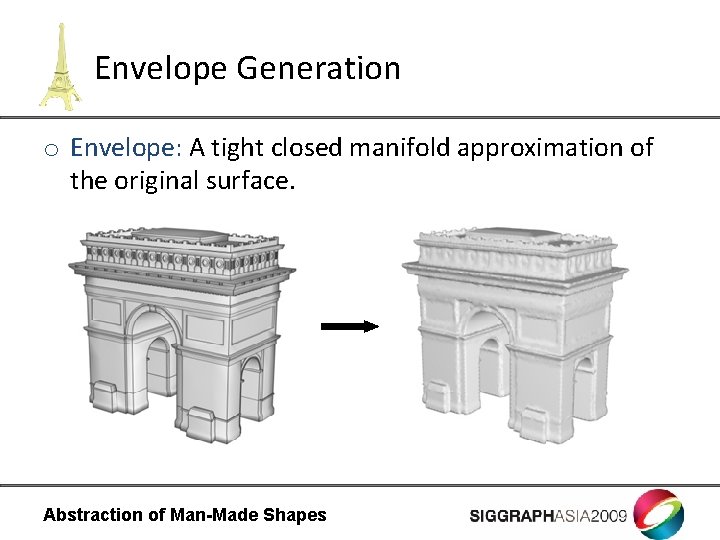
Envelope Generation o Envelope: A tight closed manifold approximation of the original surface. Abstraction of Man-Made Shapes

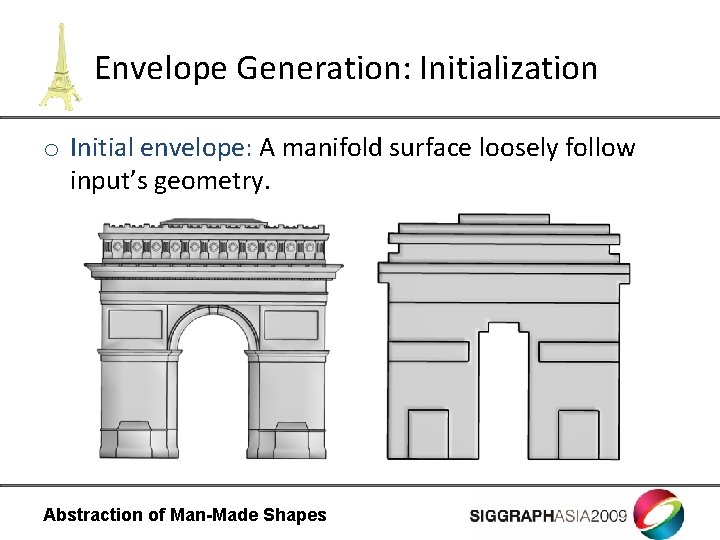
Envelope Generation: Initialization o Initial envelope: A manifold surface loosely follow input’s geometry. Abstraction of Man-Made Shapes

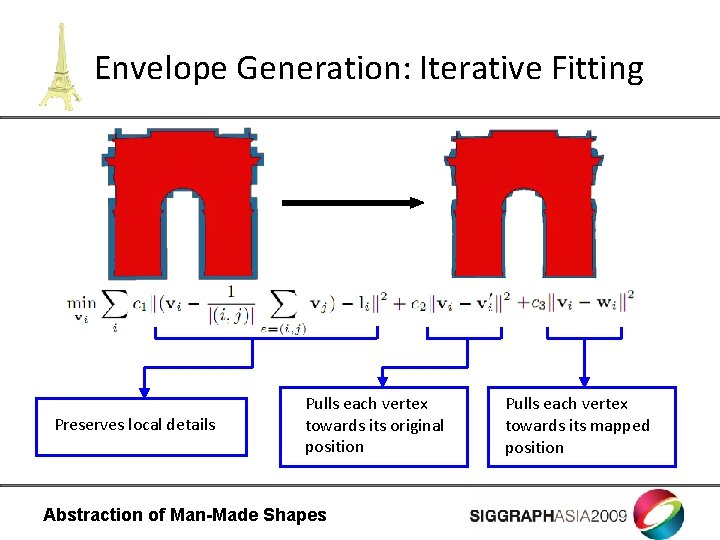
Envelope Generation: Iterative Fitting Preserves local details Pulls each vertex towards its original position Abstraction of Man-Made Shapes Pulls each vertex towards its mapped position

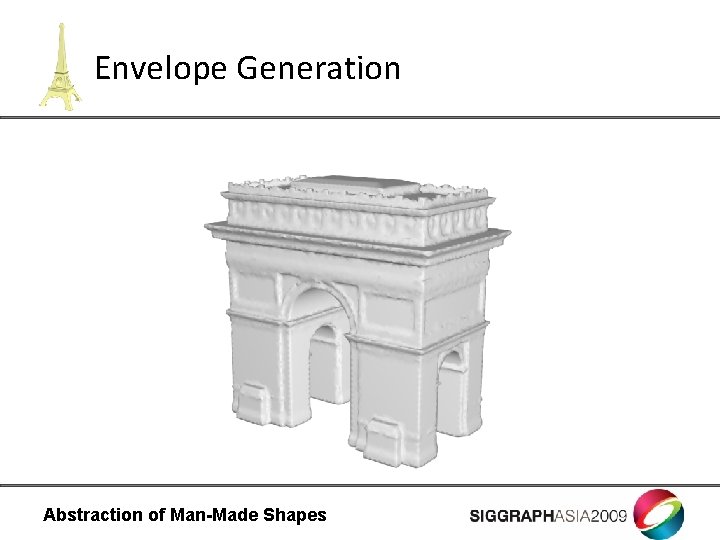
Envelope Generation Abstraction of Man-Made Shapes

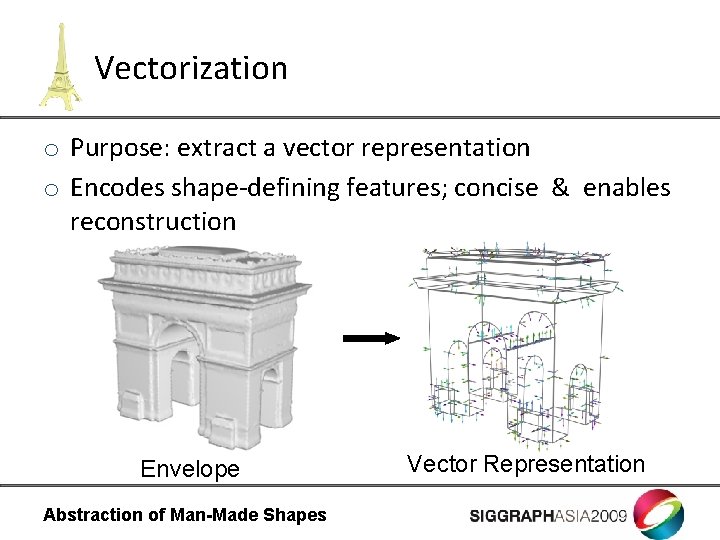
Vectorization o Purpose: extract a vector representation o Encodes shape-defining features; concise & enables reconstruction Envelope Abstraction of Man-Made Shapes Vector Representation

Vectorization as Mesh Segmentation o Man-made shapes - union of smooth patches. o Vectorization as mesh segmentation problem. • Segmentation – collection of charts • Each chart should be smooth o Vector representation = boundary of segmentation + associated normals Abstraction of Man-Made Shapes

Initial Segmentation o Variational Shape Approximation [Cohen. Steiner et al. 2004]. • Speed and simplicity • Satisfies smoothness criteria o Topological Simplification • Merging small charts • Straightening boundaries [ Julius et al. 2005 ] Abstraction of Man-Made Shapes

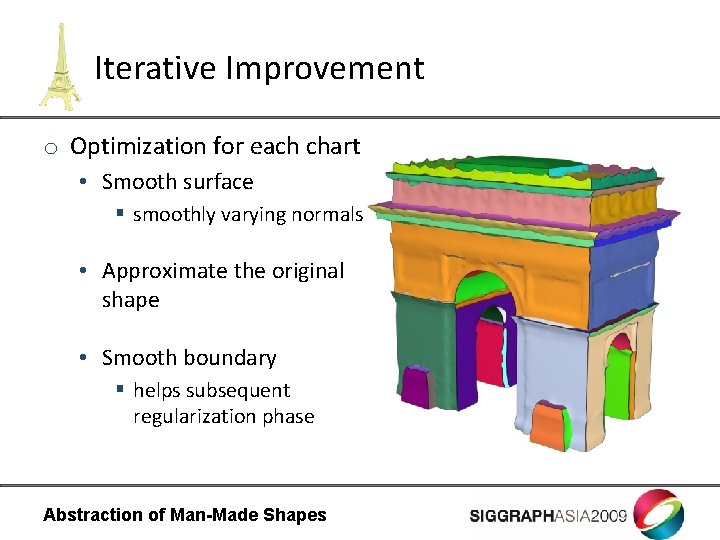
Iterative Improvement o Optimization for each chart • Smooth surface § smoothly varying normals • Approximate the original shape • Smooth boundary § helps subsequent regularization phase Abstraction of Man-Made Shapes

Iterative Improvement o Normal solve • trade-off between smoothness and original normals o Per-triangle solve • vertex positions satisfying desired normals • stay close to original positions o Global assembly • reconcile different per-triangle vertex positions Abstraction of Man-Made Shapes

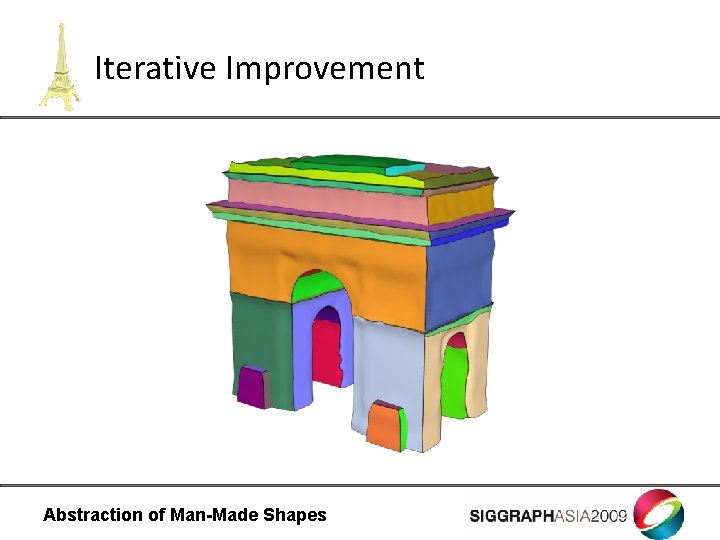
Iterative Improvement Abstraction of Man-Made Shapes

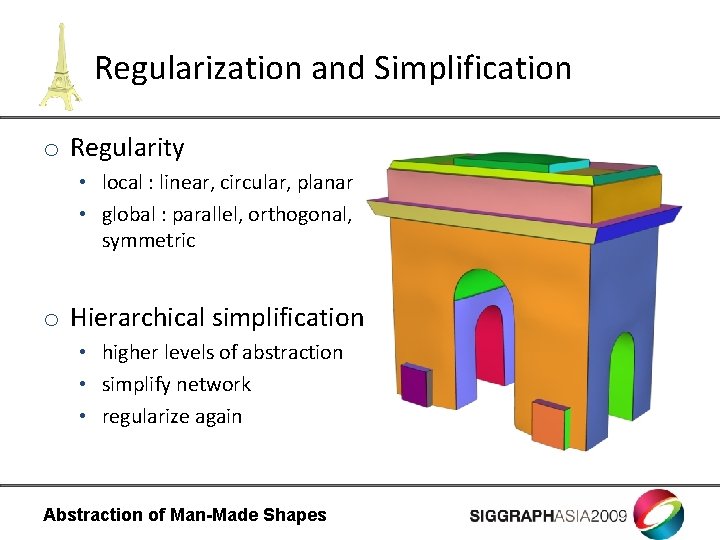
Regularization and Simplification o Regularity • local : linear, circular, planar • global : parallel, orthogonal, symmetric o Hierarchical simplification • higher levels of abstraction • simplify network • regularize again Abstraction of Man-Made Shapes

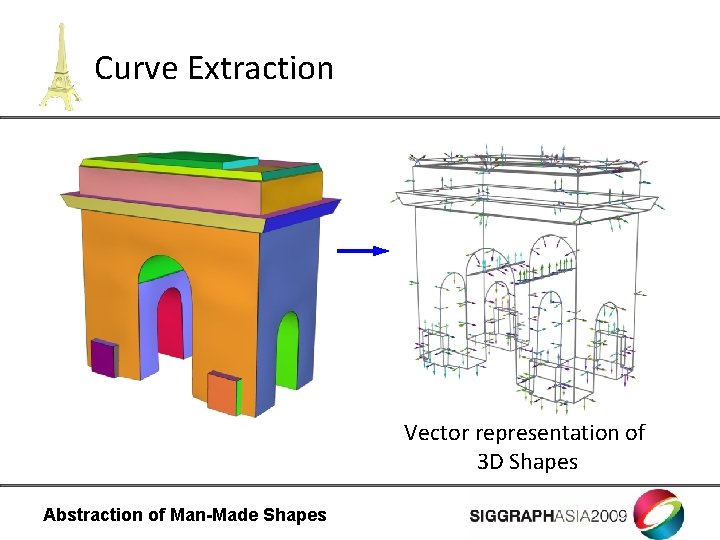
Curve Extraction Vector representation of 3 D Shapes Abstraction of Man-Made Shapes

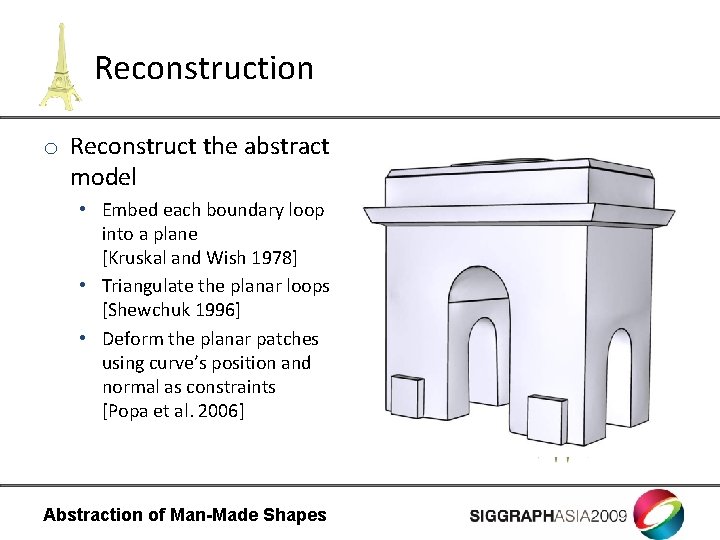
Reconstruction o Reconstruct the abstract model • Embed each boundary loop into a plane [Kruskal and Wish 1978] • Triangulate the planar loops [Shewchuk 1996] • Deform the planar patches using curve’s position and normal as constraints [Popa et al. 2006] Abstraction of Man-Made Shapes

Results Abstraction of Man-Made Shapes

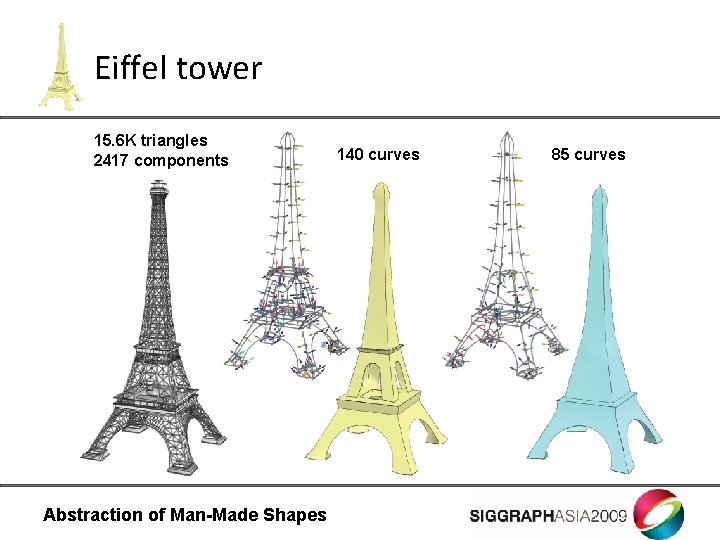
Eiffel tower 15. 6 K triangles 2417 components Abstraction of Man-Made Shapes 140 curves 85 curves

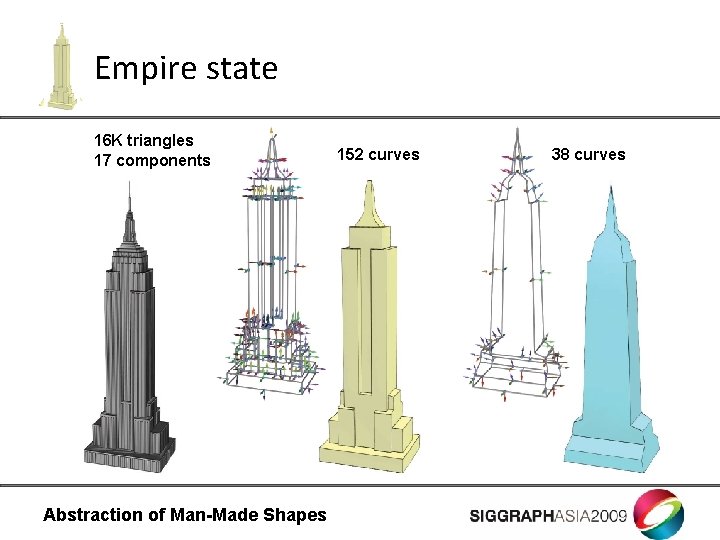
Empire state 16 K triangles 17 components Abstraction of Man-Made Shapes 152 curves 38 curves

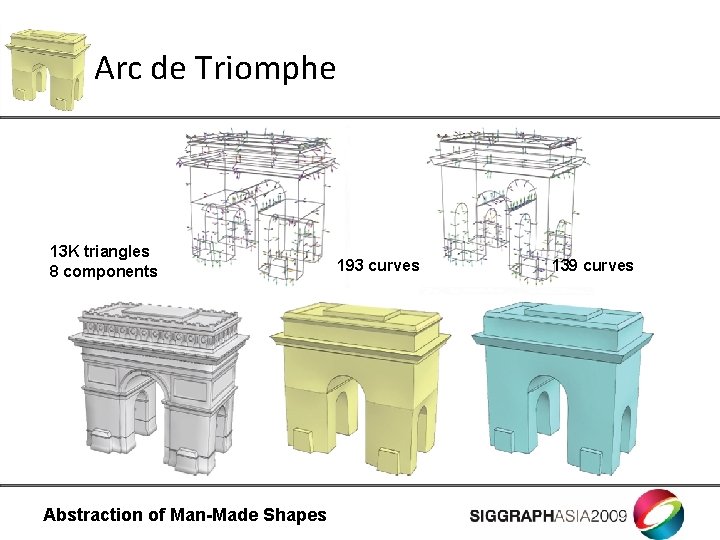
Arc de Triomphe 13 K triangles 8 components Abstraction of Man-Made Shapes 193 curves 139 curves

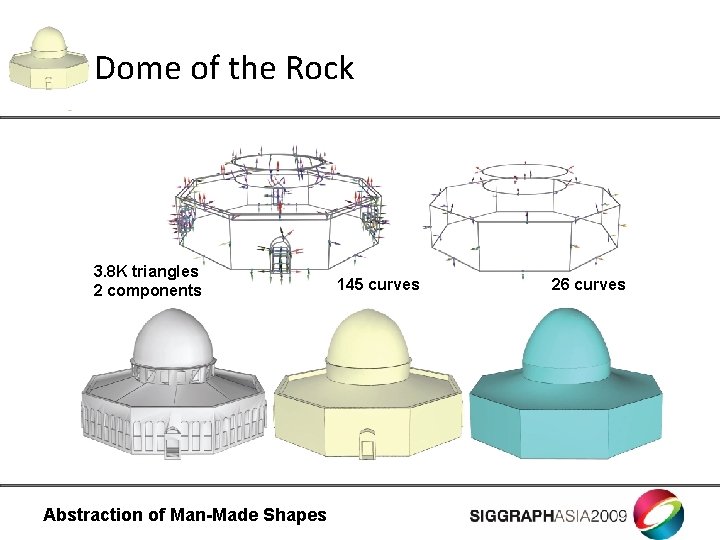
Dome of the Rock 3. 8 K triangles 2 components Abstraction of Man-Made Shapes 145 curves 26 curves

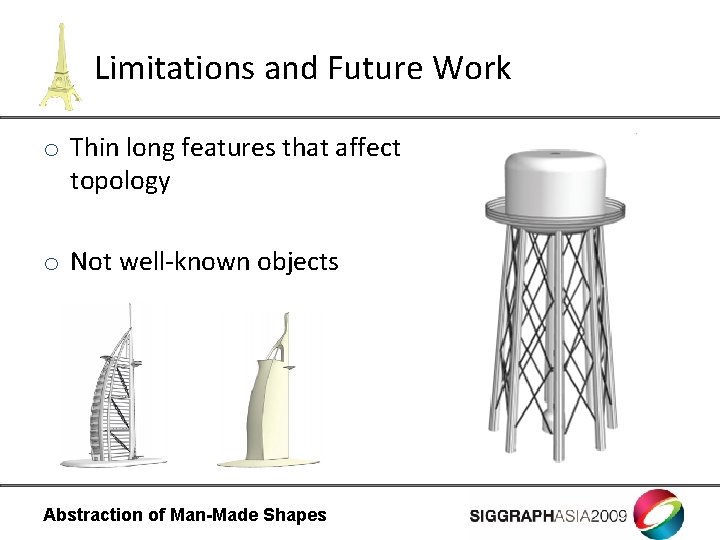
Limitations and Future Work o Thin long features that affect topology o Not well-known objects Abstraction of Man-Made Shapes

Summary o Algorithm for generating abstractions of 3 D manmade models. o Simple yet robust mechanism for approximating polygon soup by a manifold surface. o Novel vector-based representation of 3 D geometry. Abstraction of Man-Made Shapes

Acknowledgements Sponsored by Thanks Adobe Inc. MITACS NCE Microsoft Outstanding Young Faculty Fellowship NSERC Discover Program Benjamin Cecchetto Derek Bradley Karan Singh Tiberiu Popa Vladislav Kraevoy Xi Chen anonymous reviewers Abstraction of Man-Made Shapes

Abstraction of Man-Made Shapes