Abstract Syntax Tree Discrete Mathematics and Its Applications

Abstract Syntax Tree Discrete Mathematics and Its Applications Baojian Hua bjhua@ustc. edu. cn

Grammar Consider this simple grammar: n stm -> | exp -> | | id = exp; stm exp + exp - exp num id (exp) // Nonterminals: stm exp // Terminals: = ; + - ( ) num id

Grammar Sample program: n x = 3+4; y = x-(1+2); Draw the left-most derivation: n stm => id = exp; stm => … => x = 3+4; y = x-(1+2);

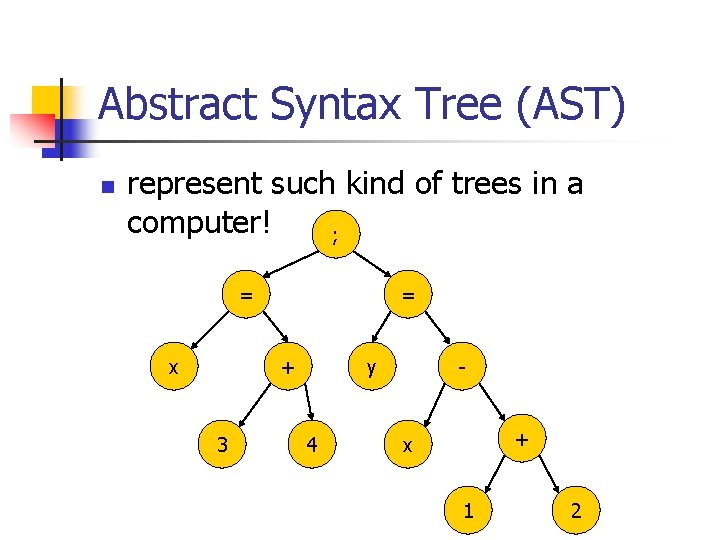
Abstract Syntax Tree (AST) n represent such kind of trees in a computer! ; = x = + 3 y 4 + x 1 2

Abstract Syntax Tree In C

Union n Recall the definition of a union: union uuu { int i; double f; }; union uuu x; x. i = 99; x. f? // Dangerous! f i

Union Operations // Or try to write a print function: void print. Union (union uuu x) { printf (“%d”, x. i); //? ? i // or f printf (“%lf”, x. f); //? ? }

Tagged Union struct tu { enum {INT, DOUBLE} kind; union uuu { int i; double f; } u; }; kind f i struct tu x; x. u. i = 99; // considered atomic operations x. kind = INT; if (x. kind==INT) … // Perfect! : -P

Tagged Union Operations // Another version of the print function: void print. Union (struct tu x) { kind switch (x. kind) { case INT: i printf (“%d”, x. u. i); f break; case DOUBLE: printf (“%lf”, x. u. f); break; default: error (…); break; } }

Or from OO’s Point of View // Some Java code abstract class Int. Or. Double {} class Int extends Int. Or. Double { int i; } class Double extends Int. Or. Double { double f; } kind f i

Local Class Hierarchy Int. Or. Double Int Double

Or from OO’s Point of View // Some Java code void print (Int. Or. Double a) { if (a instanceof Int) { Int t = (Int)a; System. out. println (t. i); } else if (a instanceof Double) { Double t = (Double)a; System. out. println (t. f); } else throw …; } kind f i

AST Recall the grammar: n stm -> | exp -> | | n id = exp; stm exp + exp - exp num id (exp) Oh, it’s just a kind of (tagged) union! : -) n Rethink the inductive definitions

The Interface #ifndef MINIC_H #define MINIC_H stm -> id = exp; stm typedef struct stm. Struct *stm; typedef struct exp. Struct *exp; struct stm. Struct { enum {ASSIGN, SEQUENCE} kind; union { struct {…} assign; struct {…} sequence; } u; }; // to be continued

The Interface struct exp. Struct { enum {ADD, SUB, NUM, ID} kind; union { exp -> exp + exp struct | exp - exp { | num exp e 1; | id exp e 2; | (exp) } binop; int num; char *id; } u; }; // functions on next slide

The Interface // interface continued // constructors for building the tree nodes stm new. Stm. Assign (char *id, exp e); stm new. Stm. Sequence (char *id, exp e, stm s); exp exp new. Exp. Add (exp new. Exp. Sub (exp new. Exp. Num (int new. Exp. Id (char #endif e 1, exp e 2); i); *id);

Implementation #include “mini. C. h” exp new. Exp. Add (exp e 1, exp e 2) { exp e = (exp)malloc (sizeof (*e)); e->kind = ADD; e->u. binop. e 1 = e 1; e->u. binop. e 2 = e 2; return e; } // others are similar, leave to you

Client Code int main () { /* We want to put: x = 3+4; y = x-(1+2); */ stm s 2 = new. Stm. Assign (“y”, new. Exp. Sub (new. Exp. Id (“x”), new. Exp. Add (new. Exp. Num(1), new. Exp. Num(2)))); stm s = new. Stm. Sequence (“x”, new. Exp. Add (new. Exp. Num(3), new. Exp. Num(4)), s 2); return 0; }

Inductively-defined Functions // Suppose we want to write a function // f: exp->{id 1, id 2, …, idn} // to compute set of the variables appear in exp. // The definition for f: { f(e)= { { { f(e 1) f(e 2), {id}, phi, if e==e 1+e 2; if e==e 1 -e 2; if e==id; otherwise. (e 1 is num)

Recursion #include “mini. C. h” set id. Set (exp e) { switch (e->kind){ case ADD: return set. Union (id. Set (e->u. binop. e 1), id. Set (e->u. binop. e 2)); case SUB: … // similar case ID: return singleton. Set (e->u. i); case NUM: return empty. Set (); default: …; } }

Abstract Syntax Tree In Java

Local Class Hierarchy abstract class Stm {} class Stm. Assign extends Stm { String id; Exp e; …; // constructors and methods } class Stm. Sequence extends Stm { String id; Exp e; Stm s; // similar }

Local Class Hierarchy abstract class Exp {} class Exp. Add extends Exp { Exp e 1; Exp e 2; … // constructors and methods } class Exp. Sub extends Exp { // similar } class Exp. Num extends Exp { int i; … // constructors and methods } class Exp. Id extends Exp { String id; }

Client Code void main (String[] args) { /* We want to put: x = 3+4; y = x-(1+2); */ Stm s 2 = new Stm. Assign (“y”, new Exp. Sub (new Exp. Id (“x”), new Exp. Add (new Exp. Num(1), new Exp. Num(2)))); Stm s = new Stm. Sequence (“x”, new Exp. Add (new Exp. Num(3), new Exp. Num(4)), s 2); return 0; }

Recursion Set<String> id. Set (Exp e){ if (e instanceof Exp. Add){ … } else if (e instanceof Exp. Sub) { … } else if (e instanceof Exp. Num) { … } else throw …; } // Or, use the visitor pattern.