Abstract data types ADT Abstract data types ADT

Abstract data types (ADT)

Abstract data types (ADT) • Abstract data type – some internal data structure + high level operations over the ADT over the structure – the user is not interested in internal implementation • they are often dynamic – the size (count of elements) is changed dynamically • operations insert element, get element, is_empty, …

Abstract data types (ADT) insert get ADT

ADT • • linked list queue (FIFO) stack (LIFO) set tree map graph etc.

ADT • we show only non-object oriented implementation of some ADT • object oriented implementation of another ADT in the future • implementation of ADT (set, fifo, …) is part of C++ standard since 1999 – STL (Standard Template Library) – you will probably never implement own ADT

Single linked list • dynamic linear list where elements are often deleted and inserted • dynamic list hardly realized as arrays: 0 1 2 3 4 5 6 7 8 9 3 6 8 12 1 8 5 7 9 -50 delete means copy 0 1 2 3 4 5 6 7 8 9 3 6 8 12 1 8 5 7 9 -50

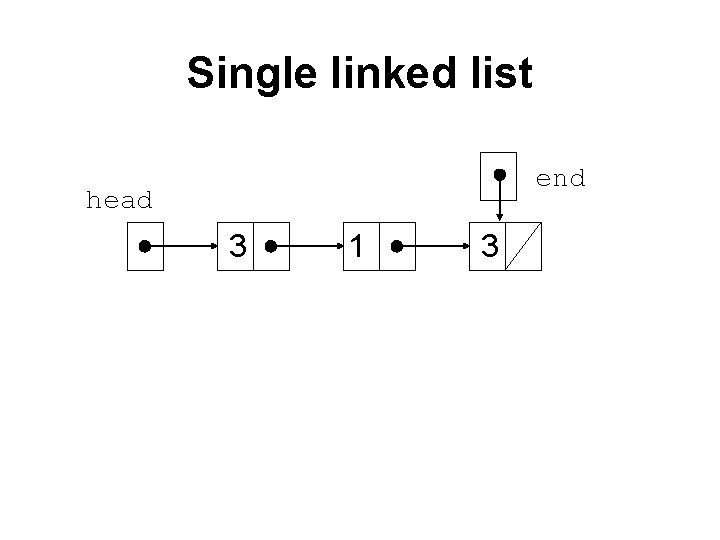
Single linked list end head 3 1 3

• implementation v C non object oriented typedef struct TElement { int item; we must put the name here TElement *next; because we reference to the } TElement; structure itself in declaration typedef struct { TElement *head; TElement *end; } TList;

TList list 1; void Init(TList *list) { list -> head = NULL; list -> end = NULL; }

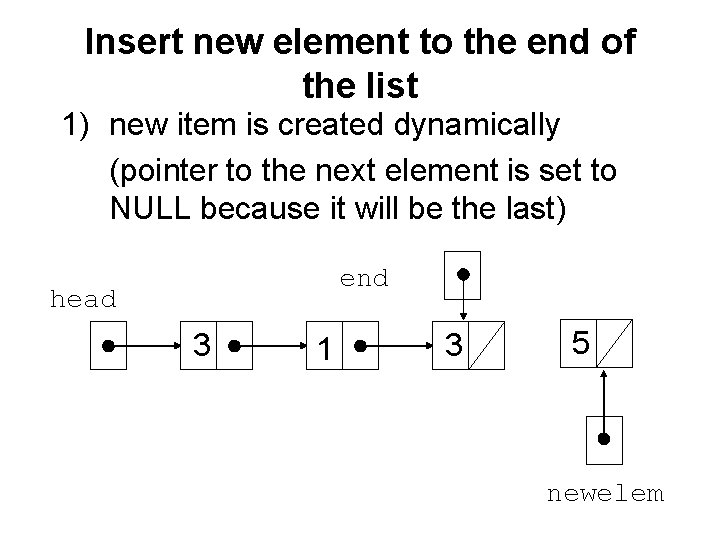
Insert new element to the end of the list 1) new item is created dynamically (pointer to the next element is set to NULL because it will be the last) end head 3 1 3 5 newelem

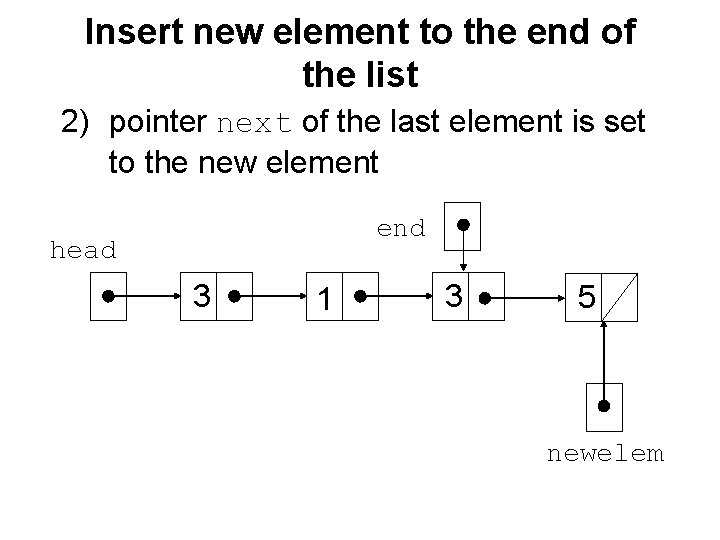
Insert new element to the end of the list 2) pointer next of the last element is set to the new element end head 3 1 3 5 newelem

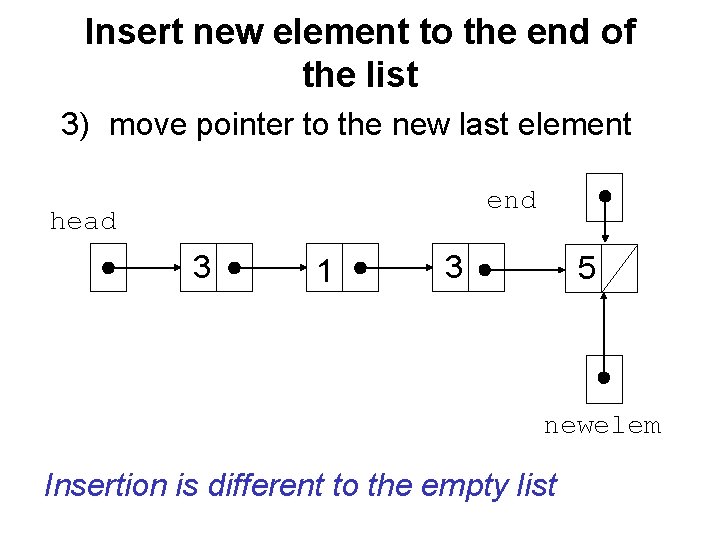
Insert new element to the end of the list 3) move pointer to the new last element end head 3 1 3 5 newelem Insertion is different to the empty list

void Insert_to_end(TList *list, int num) { TElement *newelem; newelem = (TElement*)malloc(sizeof(TElement)); newelem -> item = num; newelem -> next=NULL; if (list -> head != NULL) { list -> end -> next = newelem; list -> end = newelem; } else { list -> end = newelem; list -> head = newelem; } }

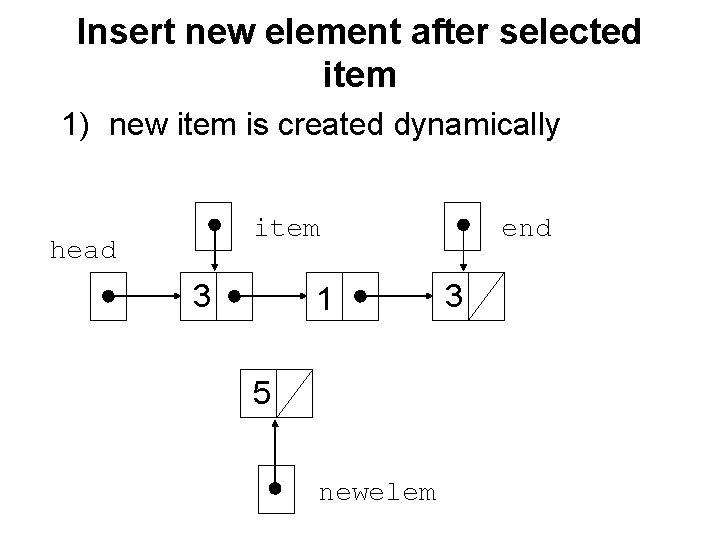
Insert new element after selected item 1) new item is created dynamically item head 3 1 5 newelem end 3

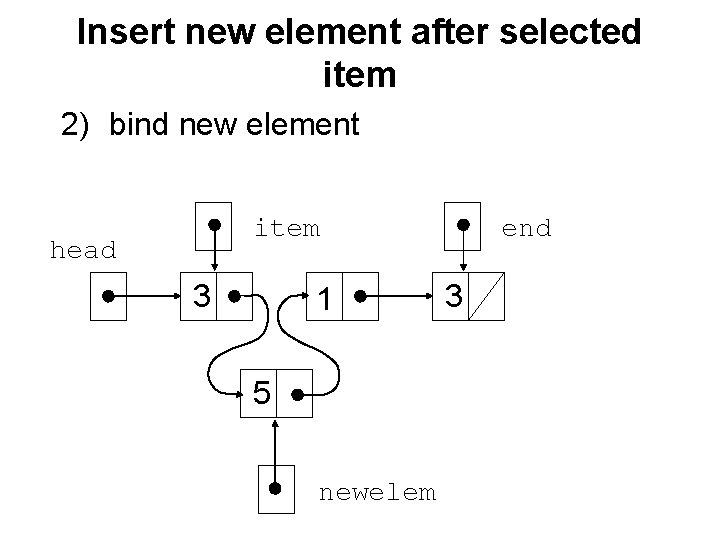
Insert new element after selected item 2) bind new element item head 3 1 5 newelem end 3

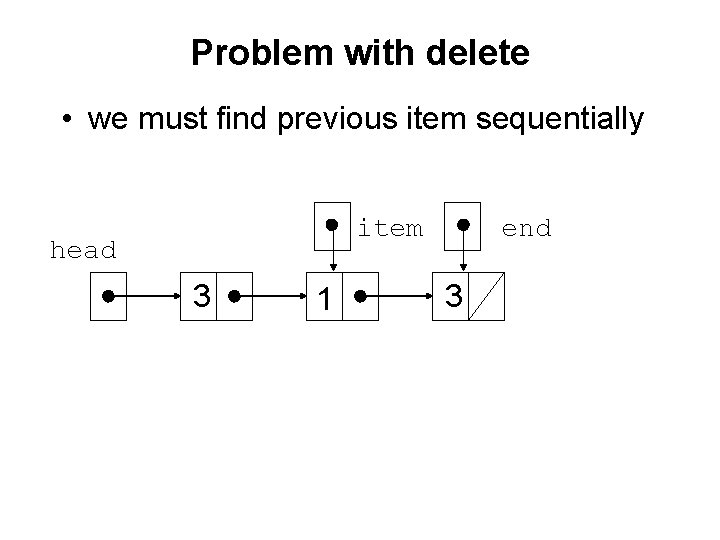
Problem with delete • we must find previous item sequentially item head 3 1 end 3

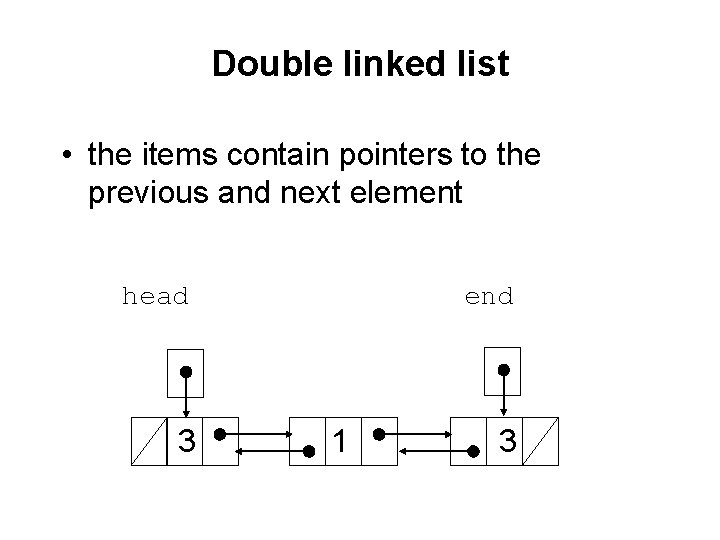
Double linked list • the items contain pointers to the previous and next element head 3 end 1 3

Example of linked list • implementation of the list of phone numbers – linked list is not so suitable for this purpose (non effective search) but illustrative

Queue (FIFO) • FIFO – First In - First Out • elements are got in the same order as inserted

Possible implementations • linked list – „infinity“ size of the fifo (limited only by the size of computer memory) – insert into queue = insert to the end of list – get element = get from the head • array – queue with the limited size – implemented as cyclic queue

Implementation with linked list • FIFO is represented by pointers to the head and to the last element

typedef struct TElement { int x; TElement *next; } TElement; typedef struct { TElement *head; TElement *end; } TFIFO;

head end NULL

head end NULL insert(3)

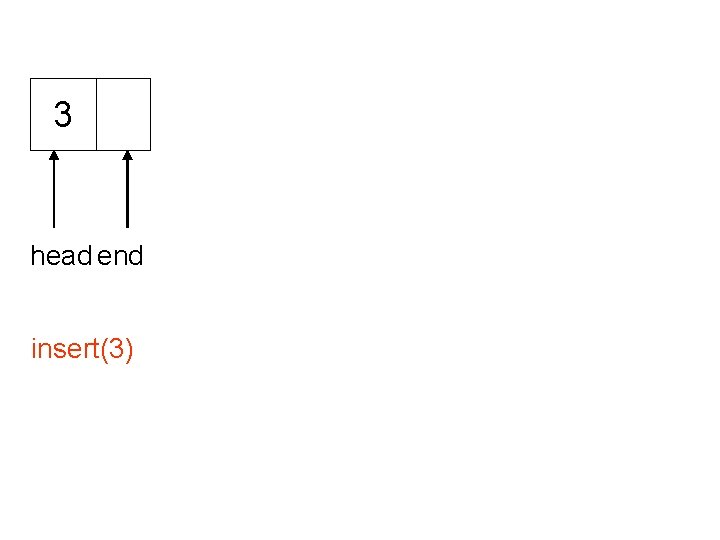
3 head end insert(3)

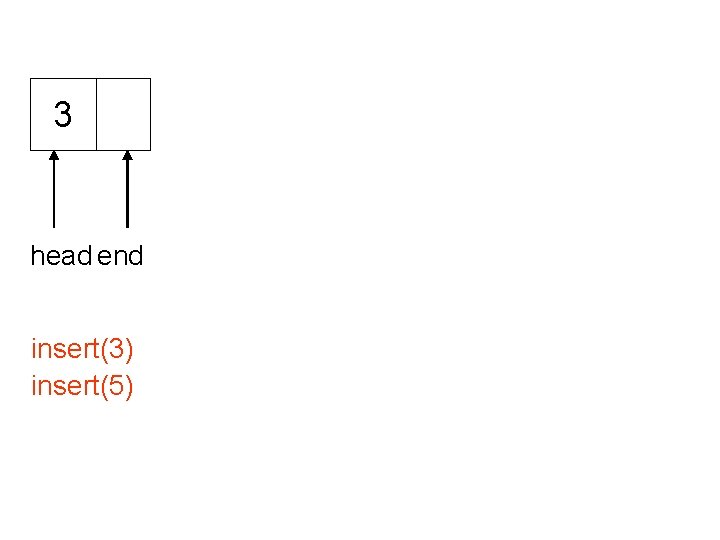
3 head end insert(3) insert(5)

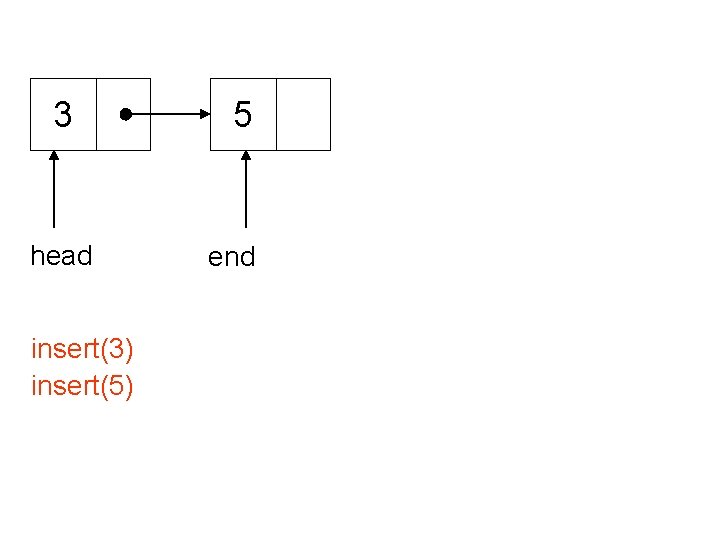
3 head insert(3) insert(5) 5 end

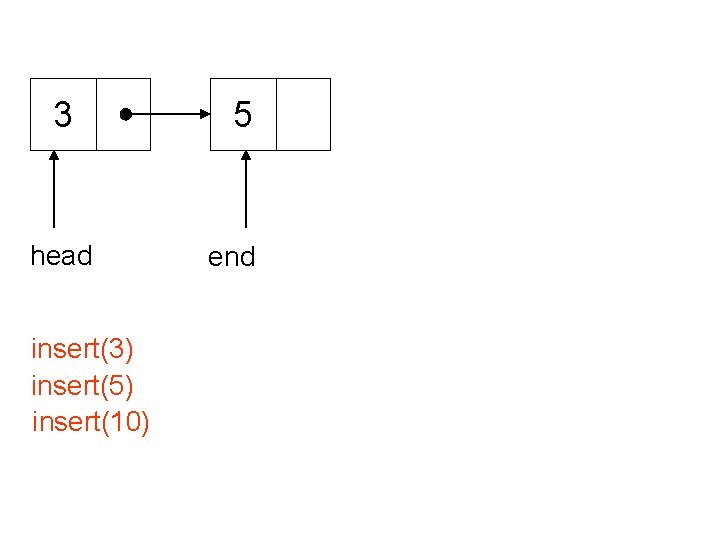
3 head insert(3) insert(5) insert(10) 5 end

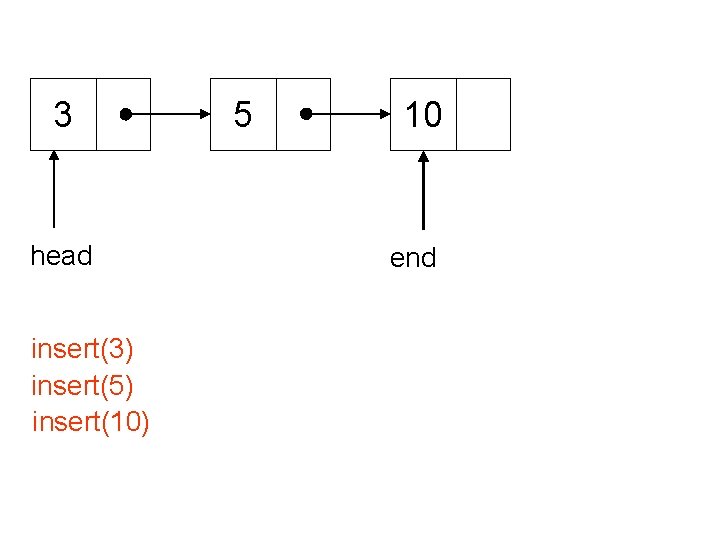
3 head insert(3) insert(5) insert(10) 5 10 end

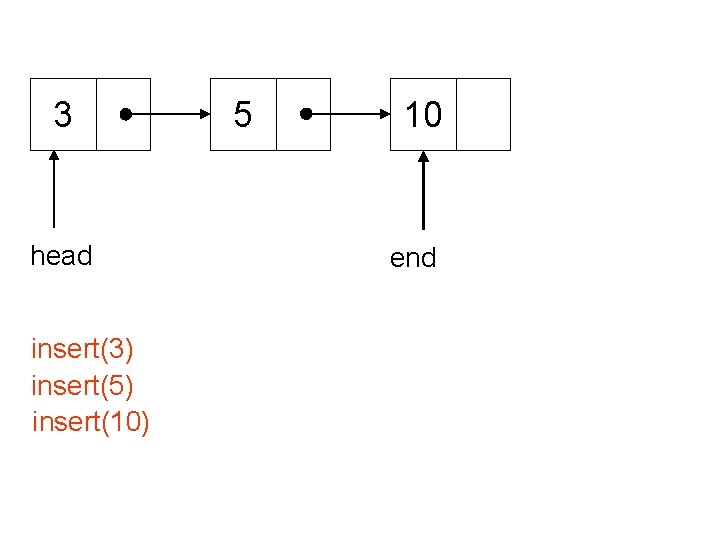
3 head insert(3) insert(5) insert(10) 5 10 end

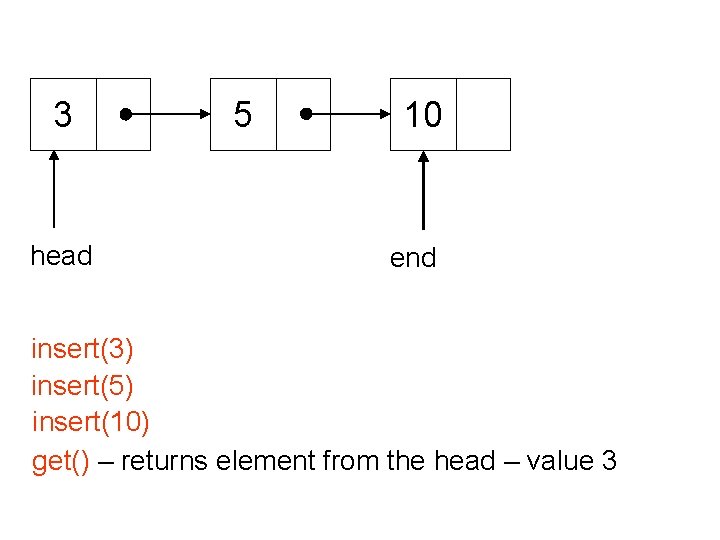
3 head 5 10 end insert(3) insert(5) insert(10) get() – returns element from the head – value 3

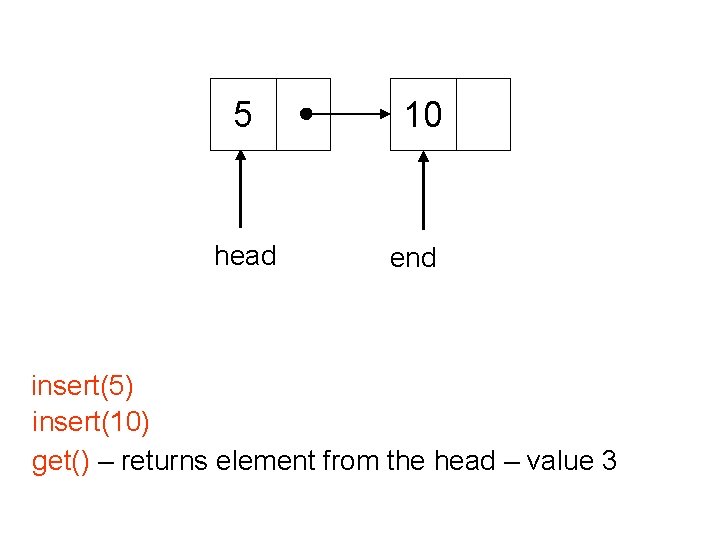
5 head 10 end insert(5) insert(10) get() – returns element from the head – value 3

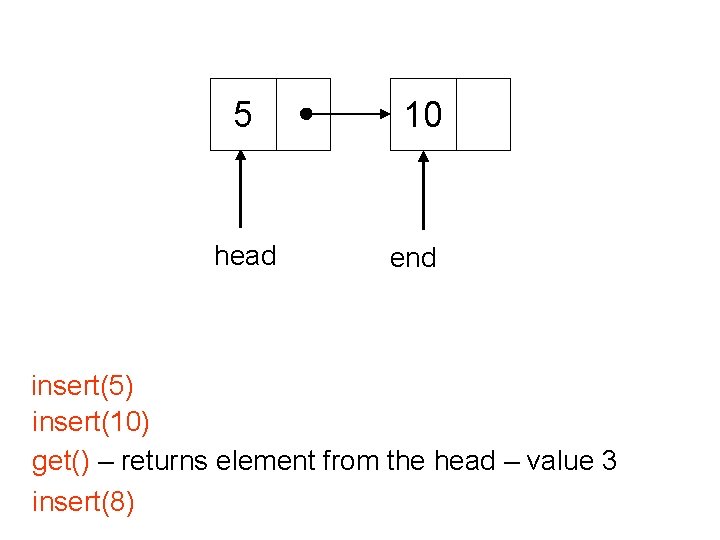
5 head 10 end insert(5) insert(10) get() – returns element from the head – value 3 insert(8)

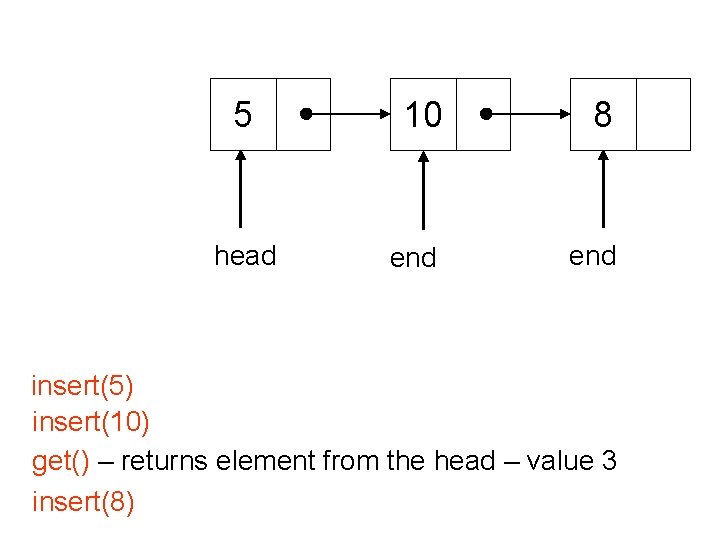
5 head 10 8 end insert(5) insert(10) get() – returns element from the head – value 3 insert(8)

Operation over FIFO void init(TFIFO *f), eventually TFIFO *init() – initialization, creates empty FIFO • int is_empty(TFIFO *f) – return true if the FIFO is empty • void insert(TFIFO *f, int item) – insert new item to the end of FIFO • int get(TFIFO *f) – returns item from the head • void delete(TFIFO *f)

int get(TFIFO *f) { int item; TElement *aux; if (f->head == NULL) return -1; item = f->head->x; aux = f->head; f->head = f->head->next; free(aux); return item; }

• it is not good solution to return -1 if an attempt to get from empty queue is done – it is not possible to distinguish if -1 is correct value or error number – better: set up error variable • solution: correctly use library functions – test before getting if FIFO is not empty – while (!is_empty(&f))

Where to use FIFO? : • queue of events in discrete-event simulation system – transportations – networks – digital systems – queuing system • breath first traversing graphs

Stack • LIFO – Last In - First Out • item inserted as last one (to the top) is got firstly • operations: – PUSH (insert new value to the top of the stack) – POP (get value from the top of the stack)

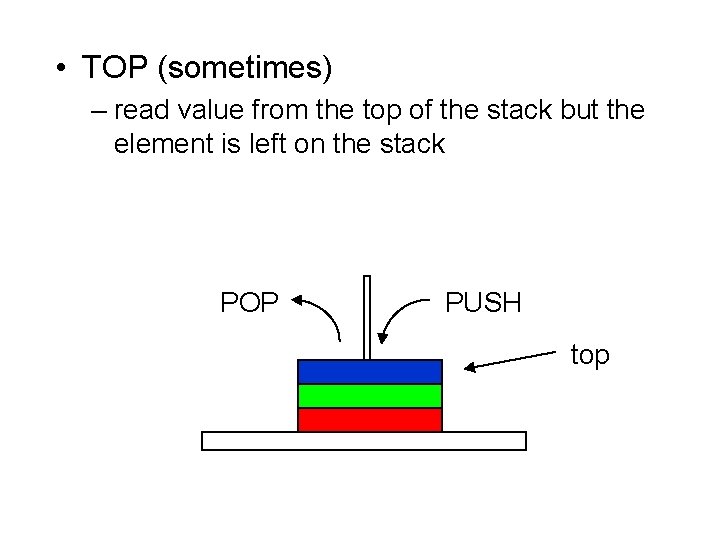
• TOP (sometimes) – read value from the top of the stack but the element is left on the stack POP PUSH top

Possible implementations • linked list – „infinity“ size of the stack (limited only by the size of computer memory) – PUSH = insert to the end of list – PUSH = get from the end of the list • array

Implementation using linked list • the stack is represented with the pointer to the top • element of the linked list carries value and the pointer to the previous element

typedef struct TElement { int x; TElement *previous; } TElement; typedef struct { TElement *top; } TStack;

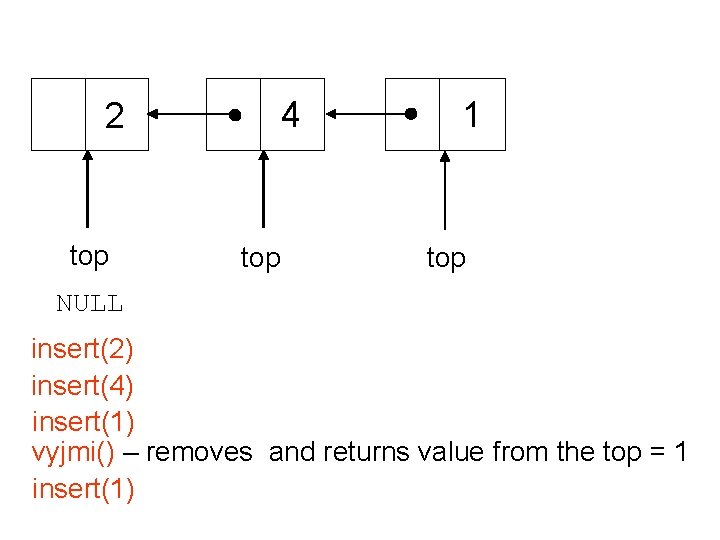
4 2 top 1 top NULL insert(2) insert(4) insert(1) vyjmi() – removes and returns value from the top = 1 insert(1)

Operation over the stack • void init(TStack *z), event. TStack *init() – inicialization, creates empty stack • int is_empty(TStack *z) – returns true if the stack is empty • void push(TStack *z, int item) – insert item to the top of the stack • int pop(TStack *z) – returns and removes item from the top of the stack • void delete(TStack *z)

TStack* init() { TStack *stack =(TStack*)malloc(sizeof(TStack)); stack->top = NULL; return stack; } int pop(TStack *z) { int item; TElement *aux; if (z->top != NULL) { item = z->top->x; aux = z->top->previous; free(z->top); z->top = aux; return item; } return -1; }

Using this stack: TStack *stack; stack = init(); push(stack, 3); push(stack, 4); pop(stack); delete(stack);

Implementation using array • relatively easy • effective implementation with resizing array

Using stack: • reverse of incoming data • elimination of the recursion • deep first traversal graphs