ABSTRACT ALGEBRA GROUP THEORY E Daniel Associate Professor

ABSTRACT ALGEBRA GROUP THEORY E. Daniel Associate Professor and HOD Dept. Of Mathematics Christian College, Chengannur

Groups

The Definition

Familiar Groups, Examples 1

Familiar Groups, Examples 2

Familiar Group, Example 3

A Strange Example So we cannot form a group using vectors and the cross product!
Symmetry Groups

Geometry and Isometries Each of the above examples of groups are “algebraic. ” We now introduce groups based on geometric properties.

Symmetry Groups
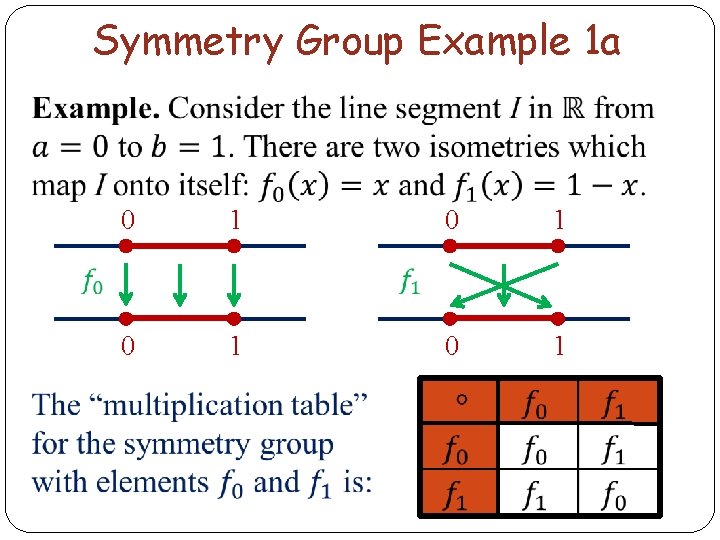
Symmetry Group Example 1 a 0 1 0 1

Symmetry Group Example 1 b
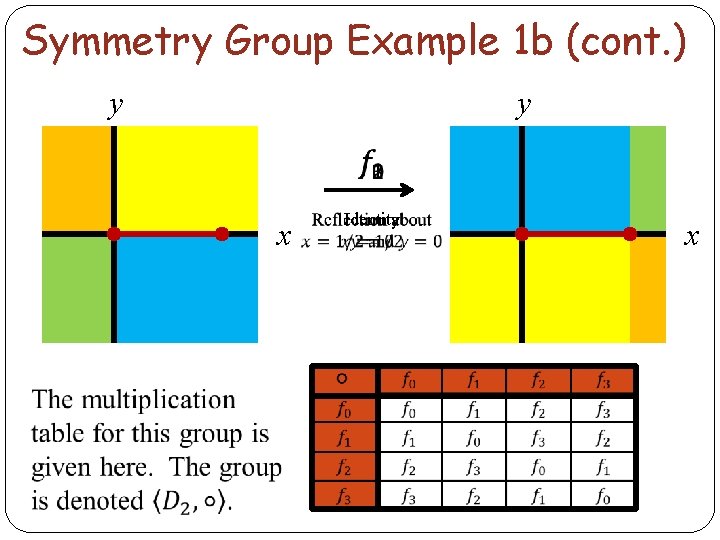
Symmetry Group Example 1 b (cont. ) y y x Identity x
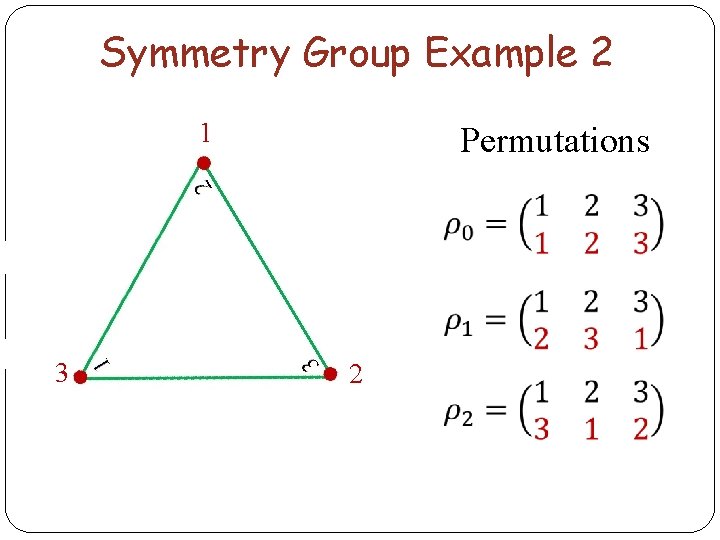
Symmetry Group Example 2 1 3 Permutations 2

Symmetry Group Example 2 (cont. ) 1 3 Permutations 2

Symmetry Group Example 2 (cont. ) 1 3 Permutations 2

Symmetry Group Example 2 (cont. ) 1 3 Permutations 2
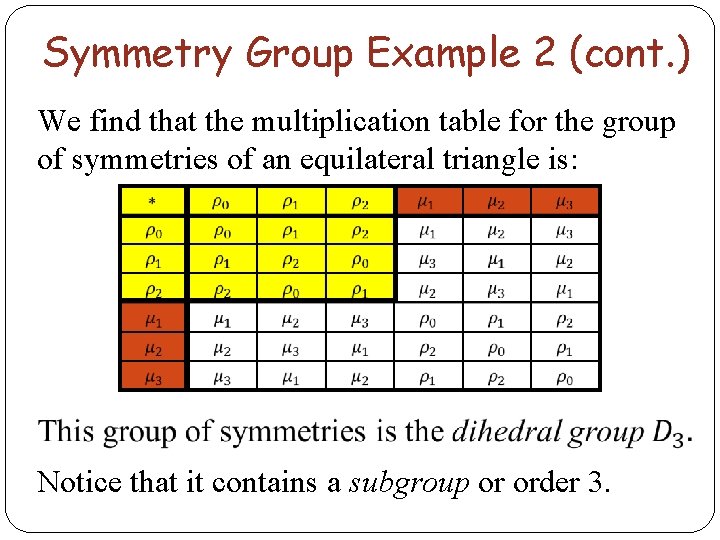
Symmetry Group Example 2 (cont. ) We find that the multiplication table for the group of symmetries of an equilateral triangle is: Notice that it contains a subgroup or order 3.
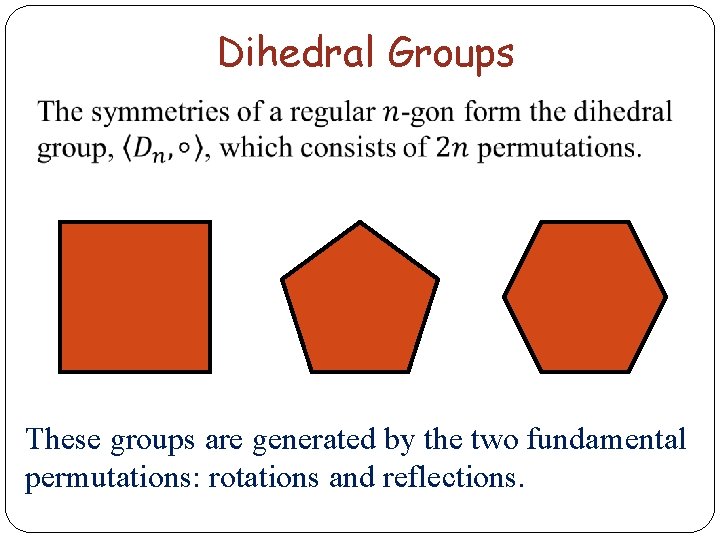
Dihedral Groups These groups are generated by the two fundamental permutations: rotations and reflections.

Cyclic Groups
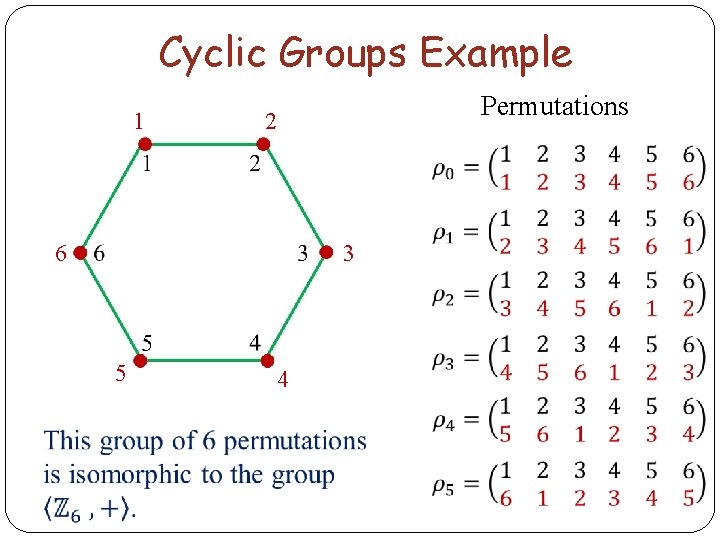
Cyclic Groups Example 1 Permutations 2 3 6 5 4

Generators of a Group

Finite Symmetry Groups We now explore infinite plane symmetry groups. This topic is covered (briefly) in Fraleigh in Section II. 12 (“Plane Isometries”) and in some detail in Gallian’s Chapter 28 (“Frieze Groups and Crystallographic Groups”).
Plane Isometries

Four Plane Isometries
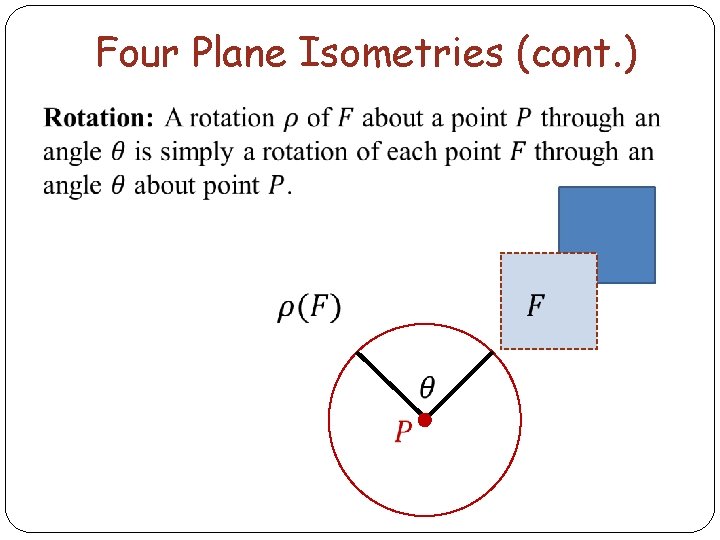
Four Plane Isometries (cont. )
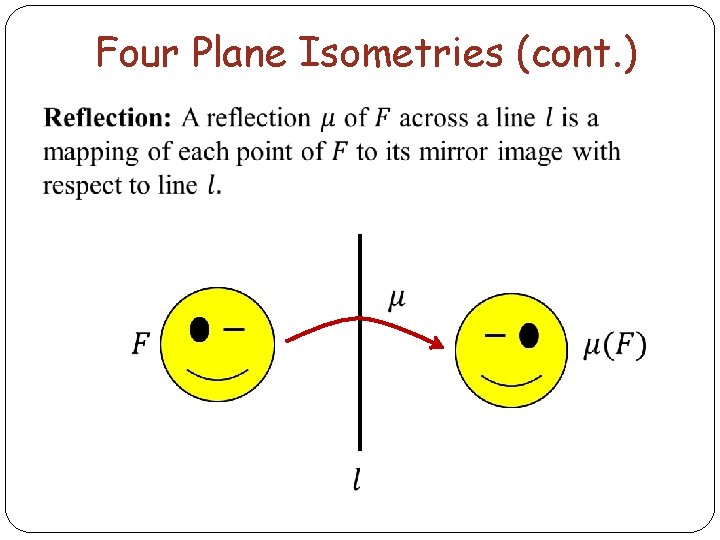
Four Plane Isometries (cont. )
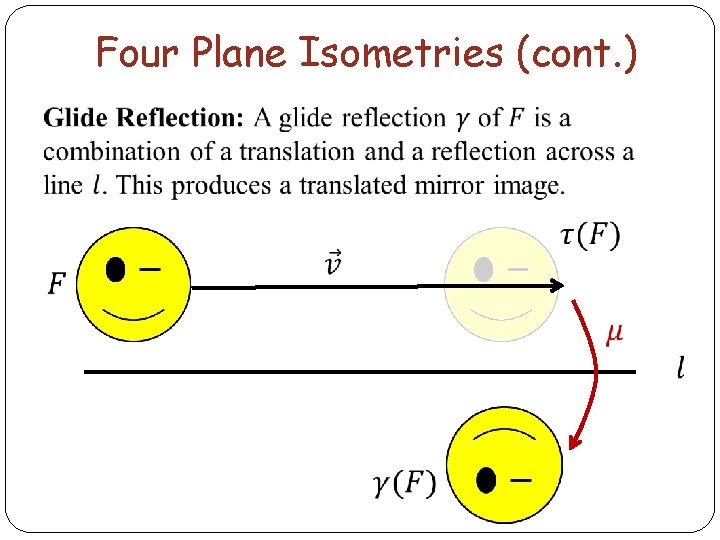
Four Plane Isometries (cont. )

Four Plane Isometries (cont. ) Translations and rotations are examples of orientationpreserving isometries (which we illustrated with squares), whereas reflections and glide reflections are examples of orientation-reversing motions (which we illustrated with winking smiley faces). [Artin, page 157] In fact, the four isometries listed above are the only isometries of the plane:

Finite Symmetry Groups, Translations, and Glide Reflections

Symmetry Groups in 3 Dimensions We can consider symmetry groups in higher dimensional spaces as well. There a total of 230 crystallographic groups in 3 dimensions. [Gallian, page 483] In 4 -dimensions, there are 4, 783 crystallographic groups. [Gallian, page 484]
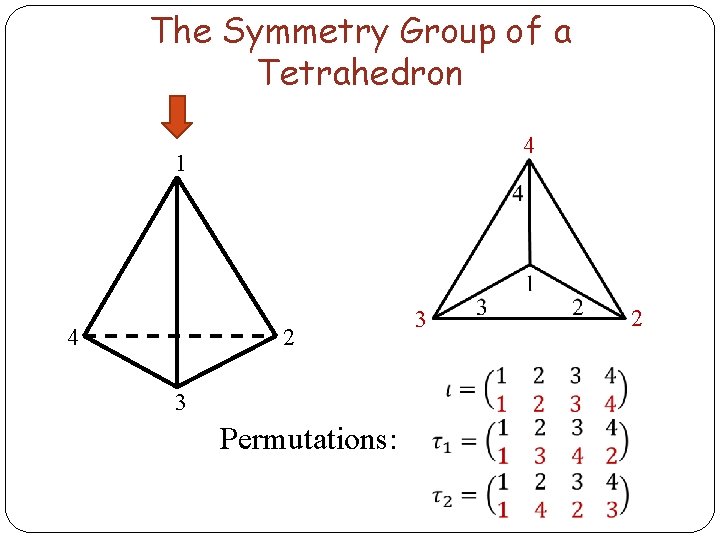
The Symmetry Group of a Tetrahedron 4 1 4 2 3 Permutations: 3 2
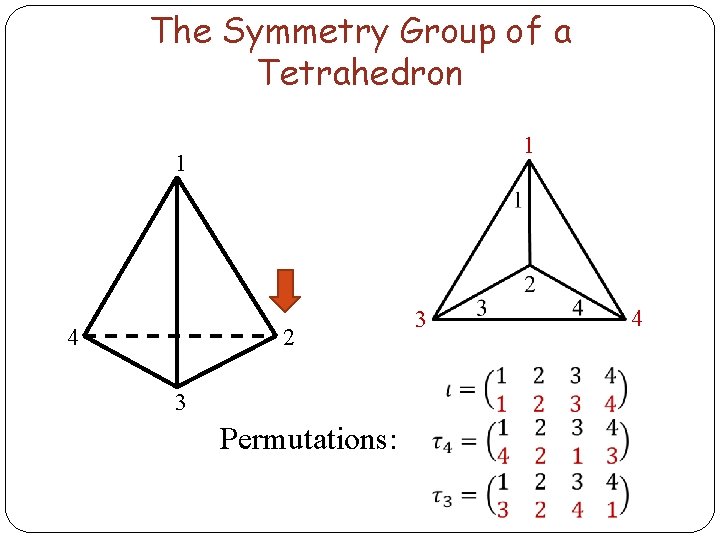
The Symmetry Group of a Tetrahedron 1 1 4 2 3 Permutations: 3 4
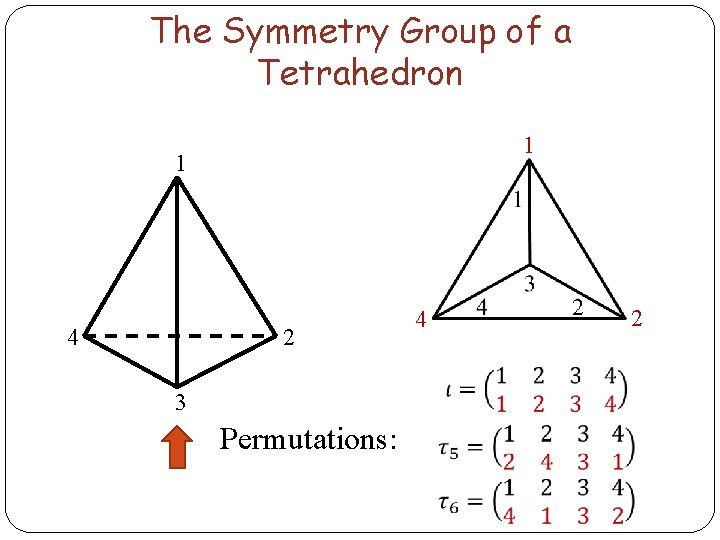
The Symmetry Group of a Tetrahedron 1 1 4 2 3 Permutations: 4 2
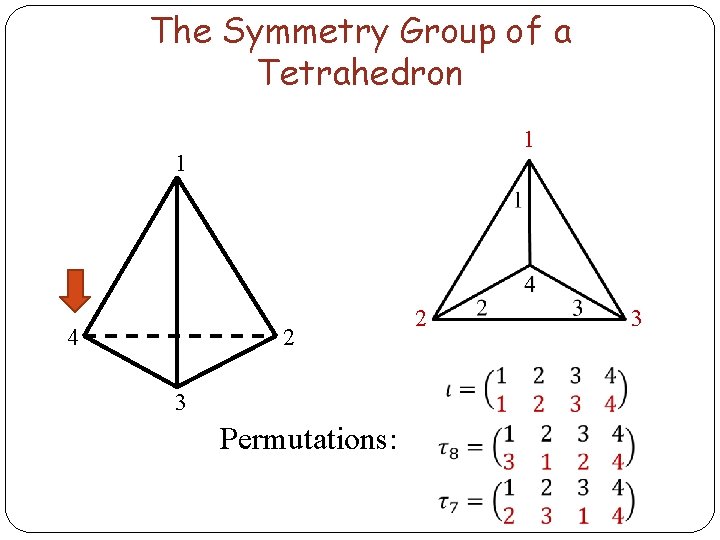
The Symmetry Group of a Tetrahedron 1 1 4 2 3 Permutations: 2 3
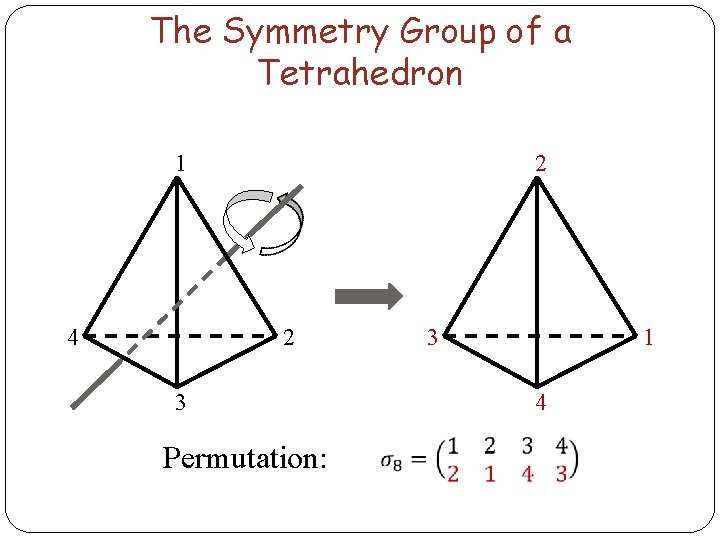
The Symmetry Group of a Tetrahedron 1 4 2 2 3 Permutation: 3 1 4
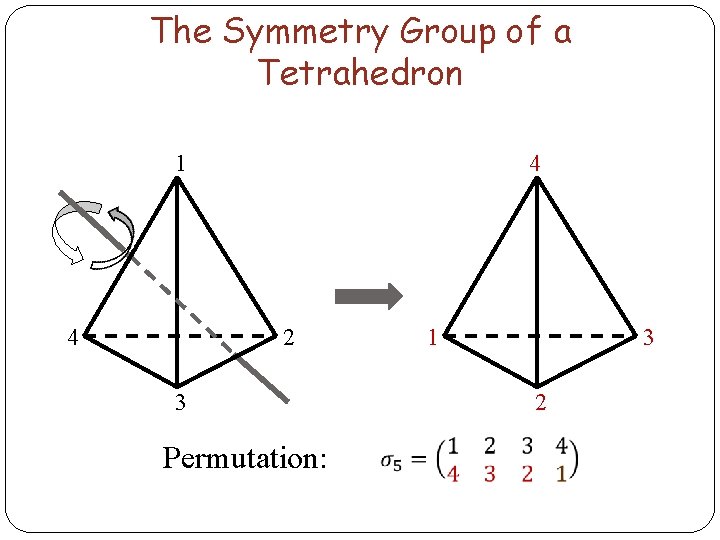
The Symmetry Group of a Tetrahedron 1 4 4 2 3 Permutation: 1 3 2
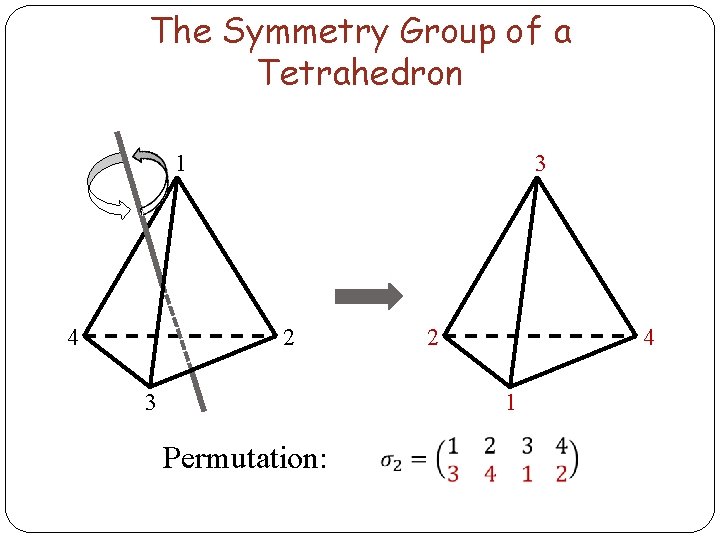
The Symmetry Group of a Tetrahedron 1 4 3 2 4 1 Permutation:
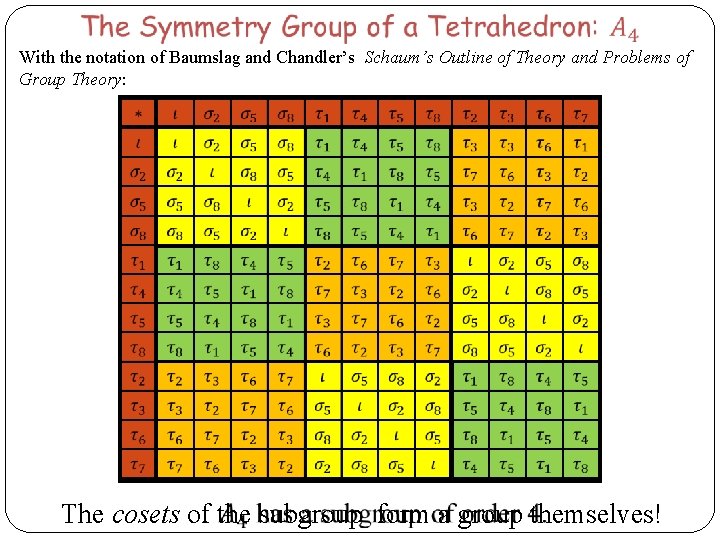
With the notation of Baumslag and Chandler’s Schaum’s Outline of Theory and Problems of Group Theory: The cosets of the subgroup form a group themselves!
References 1. Michael Artin, Algebra, Prentice-Hall (1991). 2. Benjamin Baumslag and Bruce Chandler, Schaum’s Outline of Theory and Problems of Group Theory, Mc. Graw-Hill (1968). 3. John B. Fraleigh, A First Course in Abstract Algebra, 7 th Edition, Addison-Wesley (2002). 4. Joseph A. Gallian, Contemporary Abstract Algebra, 8 th Edition, Brooks/Cole (2013). 5. Mark Ronan, Symmetry and the Monster, Oxford University Press (2006). 6. Doris Schattischneider, The Plane Symmetry Groups: Their Recognition and Notation, The American Mathematical Monthly, 85 (1978), 439 -450. 7. D. K. Washburn and D. W. Crowe, Symmetries of Culture: Theory and Practice of Plane Pattern Analysis, University of Washington Press (1988).

Websites 1. Hop David’s “ 17 Wallpaper Groups” website , an interactive site that illustrates rotations, translations, glide translations, and reflections: http: //clowder. net/hop/17 walppr. html 2. George Baloglou’s “Crystallography Now” webpage which give a brief description and rigorous classification of the seventeen planar crystallographic groups: http: //www. oswego. edu/~baloglou/103/seventeen. html 3. David Joyce’s “Wallpaper Groups” website which gives a pattern for each of the wallpaper groups and shows the rotations, translations, glide translations, and reflections for each: http: //www. clarku. edu/~djoyce/wallpaper/ 4. Martin von Gagern’s “Plane Symmetry Examples” webpage gives patterns and symmetries for the “rosette groups, ” frieze groups, and wallpaper groups: http: //www. morenaments. de/gallery/example. Diagrams/ 5. Xah Lee’s “The 17 Wallpaper Groups” website gives patterns with symmetries and generators, following the notation of Schattisschneider: http: //xahlee. info/Wallpaper_dir/c 5_17 Wallpaper. Groups. html

Thank You!
- Slides: 42