Absorption of Dilute Mixtures Graphical Equilibrium Stage Method

Absorption of Dilute Mixtures Ø Graphical Equilibrium Stage Method for Trayed Tower Ø Consider the countercurrent-flow, trayed tower for absorption (or stripping) operating under: 1. Isobaric, isothermal, continuous, steady-state flow conditions. 2. Phase equilibrium is assumed to be achieved at each of the trays between the vapor and liquid streams leaving the tray. V L Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø Each tray is treated as an equilibrium stage. Assume that the only component transferred from one phase to other is the solute. For application to an absorber let: L' = molar flow rate of solute-free absorbent V' = molar flow rate of solute-free gas (carrier gas) X = mole ratio of solute to solute-free absorbent in the liquid = moles of solute/ mole of solute free-absorbent (solvent) Y = mole ratio of solute to solute-free gas in the vapor = moles of solute / moles of solute-free gas (inert gas) Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø With these definitions, values of L' and V' remain constant through the tower, assuming that: Ø no vaporization of absorbent into carrier gas. Ø no absorption of carrier gas by liquid. E. g. (air + NH 3) + H 2 O(solvent) carrier no H 2 O evaporate with air no absorption of air in H 2 O. solute Ø For the solute at any equilibrium stage n, the K-value is given in terms of X and Y as: Y n n (1) Xn Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures where Y = y/(1 - y) and X = x/(1 - x ). Ø The balances are written around one end of the tower and an arbitrary intermediate equilibrium stage n. Ø For the absorber (solute balance): (2) Yn+1 L` Xn V` Yn+1 Y 1 X 0 Ch. E 334: Separation Processes XN Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø or, solving for Yn+1 (3) Ø Equation (3). which is called operating-line equations, is plotted as shown in the last Figure. Ø The terminal points of this line represent the conditions at the top and bottom of the towers. Ø The operating line is above the equilibrium line because, for a given solute concentration in the liquid, the solute concentration in the gas is always greater than the equilibrium value (driving force from mass transfer of solute from the gas to the liquid). Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø The operating line is straight line with a slope of L`/ V`. Ø The terminal point of the operating line at the top of the tower is fixed at X 0 by the amount of solute. Ø The terminal point of the operating line at the bottom of the tower depend on Yn+1 and the slope of the operating line and, thus, the flow rate, L` of solute-free absorbent. Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø Minimum Absorbent Flow Rate Ø Operating lines for four different absorbent flow rates shown in Figure 6. 9 (Seader) as shown below, where each operating line passes through the terminal point, (Y 1, X 0), at the top of the column and corresponds to a different liquid absorbent rate and corresponding slope, L'/ V'. Moles solute/mole solute-free liquid, X X 0 (liquid in) Ch. E 334: Separation Processes XNmin (for L min) Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø To achieve the desired value of Y 1 for given YN+I , X 0, and V', the solutefree absorbent flow rate L', must lie in the range of (operating line 1) to L`min (operating line 4) Ø Solute balance for the entire absorber (6) (7) N= number of stage in the absorber Notes: The operating line can terminate at the equilibrium line, as operating line 4, but can not cross it because that would be a violation of the second law of thermodynamics (it is not possible to transfer a mass from the low concentration to the higher concentration) Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø The value of L`min corresponds to a value of XN (leaving the bottom of the tower) in equilibrium with YN+1, the solute concentration in the feed gas. Ø It takes an infinite number of stages for this equilibrium to be achieved. Ø For stage N, eqn. (1) becomes, for the minimum absorbent (8) Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø Solving (8) for XN and substituting the result into (7) gives: (9) Ø For dilute-solute conditions, where Y y and X x, (9) approach (10) (fraction of solute absorbed) Ch. E 334: Separation Processes (11) Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø This equation is reasonable because it would be expected that L`min would increase with increasing V`, K-value, and fraction of solute absorbed. Ø The selection of the actual operating absorbent flow rate is based on some multiple of L`min, typically from 1. 1 to 2. A value of 1. 5 corresponds closely to the value of 1. 4 for the optimal absorption factor mentioned earlier Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø NUMBER OF EQUILIBRIUM STAGES operation Ø As shown in Figure (a). the operating line relates the Solute concentration in the vapor passing upward between two stages to the solute concentration in the liquid passing downward between the same two stages. (a) Ø Figure (b) illustrates that the equilibrium curve relates the equilibrium solute concentration in the vapor leaving an equilibrium stage to the salute concentration in the liquid leaving the same stage. Ch. E 334: Separation Processes (b) Dr Saad Al-Shahrani

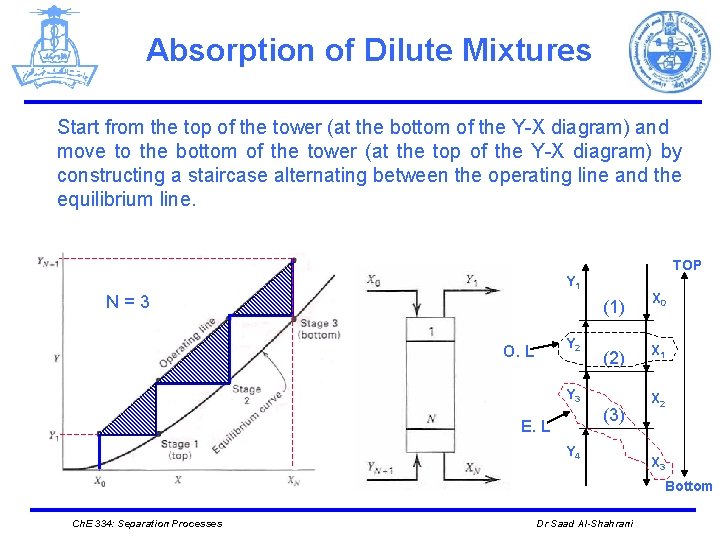
Absorption of Dilute Mixtures Start from the top of the tower (at the bottom of the Y-X diagram) and move to the bottom of the tower (at the top of the Y-X diagram) by constructing a staircase alternating between the operating line and the equilibrium line. TOP Y 1 N=3 Y 2 O. L (1) X 0 (2) X 1 Y 3 (3) E. L Y 4 X 2 X 3 Bottom Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Example: When molasses is fermented to produce a liquor containing ethyl alcohol, a CO 2 rich vapor containing a small amount of ethyl alcohol is evolved. The alcohol can be recovered by absorption with water in a sieve-tray tower. For the following conditions, determine the number of equilibrium stages required for countercurrent flow of liquid and gas, assuming isothermal, isobaric conditions in the tower and neglecting mass transfer of all components except ethyl alcohol. The entering liquid flow rate is 1. 5 times the minimum value. Entering gas: 180 kmol/h, 98% CO 2, 2% ethyl alcohol: 30°C, 110 k. Pa Entering liquid absorbent: 100% water; 30°C, 110 k. Pa Required recovery (absorption) of ethyl alcohol: 97% Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Solution Ø Assume that the exiting absorbent will be dilute alcohol, whose K-value is determined from a. modified law, K = Psat/P. The vapor pressure of ethyl alcohol at 30 o. C= 10. 5 kpa. At infinite dilution in water activity coefficient of ethyl alcohol is taken as 6. 0 therefore, K = 6*10. 5/110 = 0. 57 (fraction of solute absorbed) V`= 180*0. 98 = 176. 4 kmol/ h Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures L`min = (176. 4)(0. 57)(0. 97) = 97. 5 kmol/h The actual solute-free absorbent rate are 1. 5 times the minimum L` = (1. 5) L`min = (1. 5)(97. 5) = 146. 2 kmol/h The amount of ethyl alcohol transferred from the gas to the liquid acid is 97% of the amount of alcohol in the entering gas, or (0. 97)(0. 02)(180)=3. 49 kmo/h the amount of ethyl alcohol remaining in the exiting gas is: (1 -0. 97)(0. 02)(180) = 0. 11 kmol/h we now compute the alcohol mole ratios at both ends of the operating line as follows: Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures top bottom X 0 =0, Y 1 =(0. 11)/ (176. 4) = 0. 0006 YN+1 = (0. 11+3. 49)/(176. 4)= 0. 0204 XN =(3. 49)/ (146. 2) = 0. 0239 The equation for the operating line with X 0 = 0 is Ø The equilibrium curve for ethyl alcohol can be determined using the value of K = 0. 57 computed above. Ch. E 334: Separation Processes Dr Saad Al-Shahrani

Absorption of Dilute Mixtures Ø Solving for Y, we obtain Ø Or this dilute system in ethyl alcohol, the maximum error in Y is 1. 0% if Y is taken simply as Y = KX = 0. 57 X Ø The equilibrium curve, which is almost straight in this example. Ch. E 334: Separation Processes Dr Saad Al-Shahrani

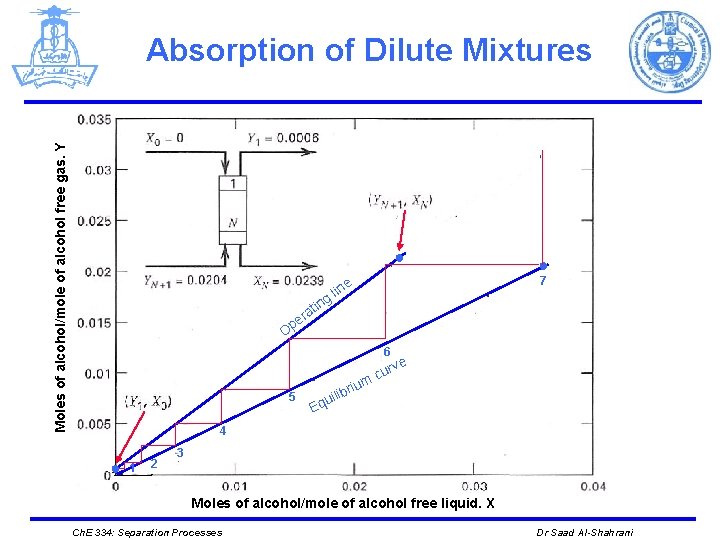
Moles of alcohol/mole of alcohol free gas. Y Absorption of Dilute Mixtures ● g in at r pe ● 7 e lin O 6 5 ve cur m briu uili q E 4 ● 1 2 3 Moles of alcohol/mole of alcohol free liquid. X Ch. E 334: Separation Processes Dr Saad Al-Shahrani