Absolute Value Functions and Graphs Two variables Inequalities

Absolute Value Functions and Graphs. Two variables Inequalities. n r a e l l ’l u o y t Wha To graph absolute value functions To graph two variables inequalities y r a l u b a c o V Absolute value function, axis of symmetry, vertex, linear inequality, test point, boundary, half-plane

Problem 1: Graphing an Absolute Value Function What is the graph of the absolute value How is this graph different from the graph of the parent function Make a table of values and graph x y=lxl-4 -3 -1 -1 -3 0 -4 1 -3 3 -1 Since the vertex is (0, -4), you translated the graph of y=lxl down 4 units

Notes The simplest example of an absolute value function is f(x). The graph of the value of a linear function in two variables is V- shape and symmetric about a vertical line called the axis of symmetry. Such a graph has either a single maximum point or a single minimum point called vertex Parent function y=lxl Vertical Translation up k units, k>0 y=lxl+k Translation down k units, k>0 y=lxl-k Vertical Stretch and Compression Vertical Stretch, a>1 y=alxl Vertical Compression, 0<a<1 y=alxl Horizontal Translation right h units, h>0 y=lx-hl Translation left h units, h>0 y=lx+hl Reflection In the x-axis y=-lxl In the y-axis y=l-xl

Problem 2: Combining Translations A. What is the graph of the function y=lx-2 l+1? B. What is the graph of the function y=2 lxl? C. What is the graph of each function

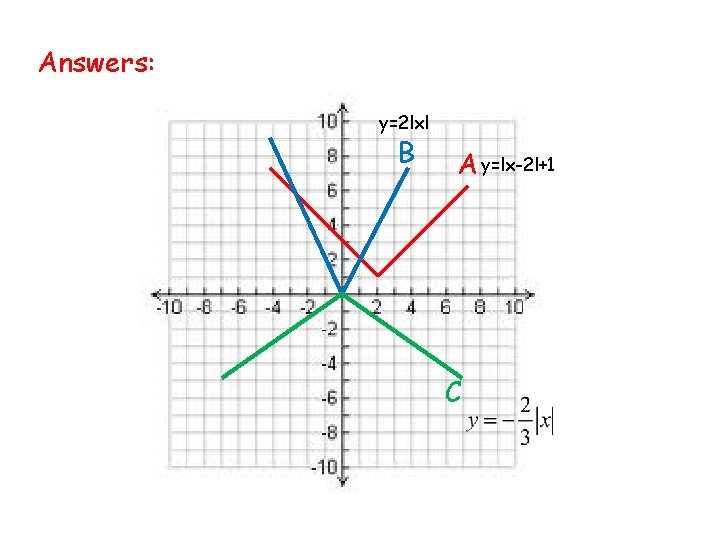
Answers: y=2 lxl B A y=lx-2 l+1 C

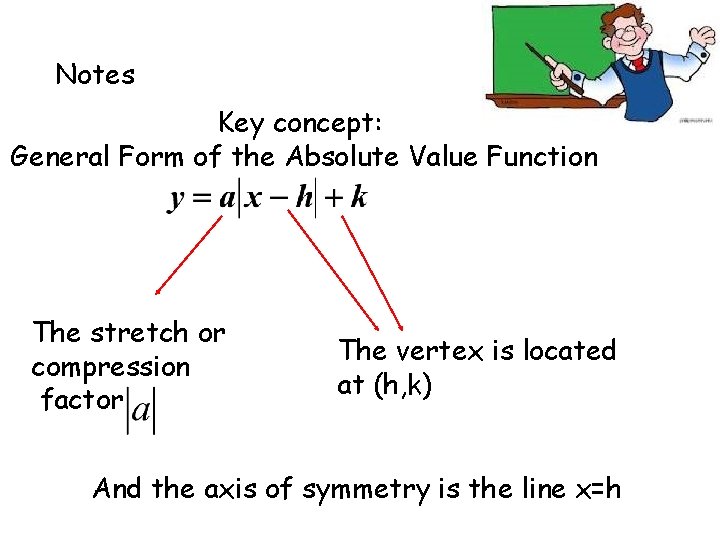
Notes Key concept: General Form of the Absolute Value Function The stretch or compression factor The vertex is located at (h, k) And the axis of symmetry is the line x=h

Problem 3: Identifying Transformations Without graphing, what is the vertex and axis of symmetry of the graph a=3 h=2 and k=4 The vertex (2, 4) and the axis of symmetry is x=2 The parent function is translated 2 units to the right , vertically stretched by the factor 3, and translated 4 units up

Problem 4: Writing Absolute Value Function What is the equation of the absolute value function? Answer: Note: the right branch of the graph of has slope 1. The graph of a>0, is a stretch or compression of the graph of. It’s right branch has slope a. The graph of is a reflection of in the x-axis and its right branch has slope –a.

Your turn 1. Which of the following is the graph of ? B 2. What is the graph of ? What are the transformations of the parent function? Vertical compression by the factor and reflection on the x-axis 3. Compare with the parent function. Without graphing, what are the vertex, axis of symmetry, and transformations of the parent function? Vertex( -2, 3), axis of symmetry x=-2 translated 2 units left Vertically stretched by the factor 2, reflected in the x-axis and translated 3 units up

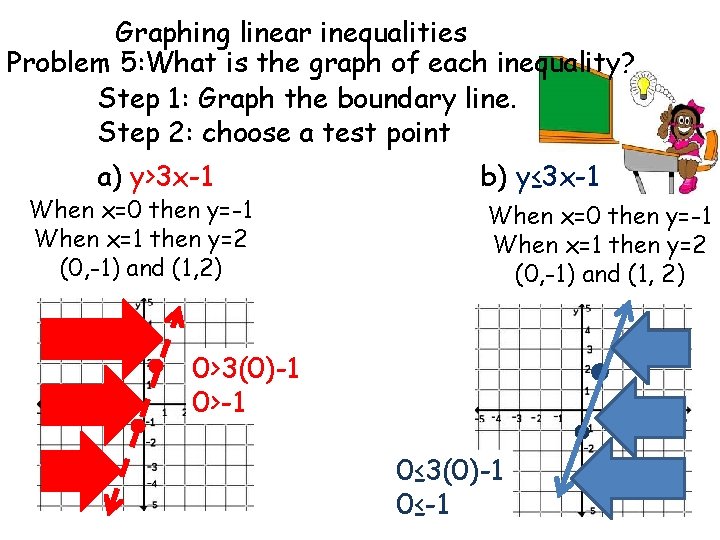
Graphing linear inequalities Problem 5: What is the graph of each inequality? Step 1: Graph the boundary line. Step 2: choose a test point a) y>3 x-1 When x=0 then y=-1 When x=1 then y=2 (0, -1) and (1, 2) b) y≤ 3 x-1 When x=0 then y=-1 When x=1 then y=2 (0, -1) and (1, 2) 0>3(0)-1 0>-1 0≤ 3(0)-1 0≤-1

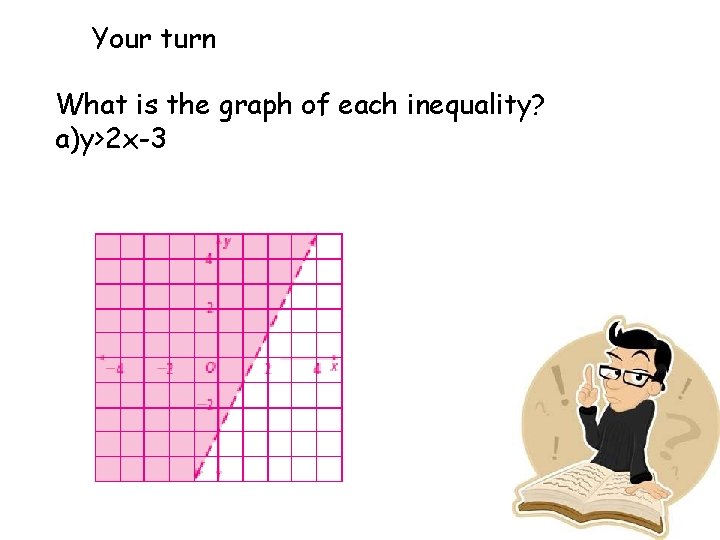
Your turn What is the graph of each inequality? a)y>2 x-3

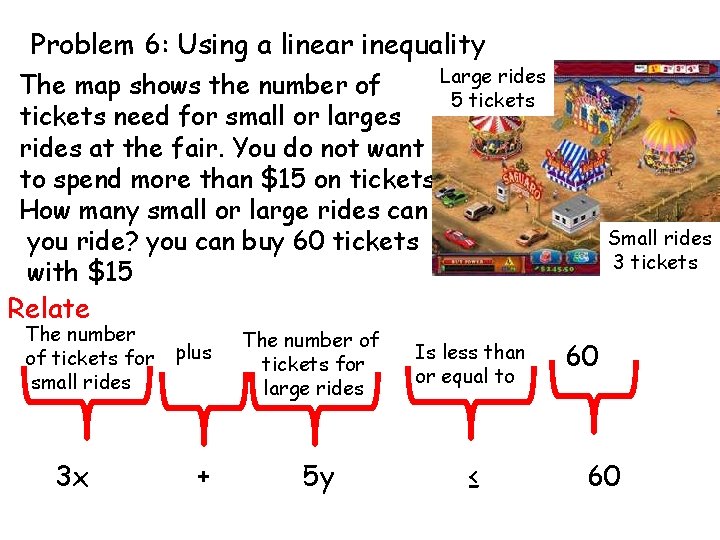
Problem 6: Using a linear inequality Large rides The map shows the number of 5 tickets need for small or larges rides at the fair. You do not want to spend more than $15 on tickets. How many small or large rides can you ride? you can buy 60 tickets with $15 Relate The number of tickets for small rides 3 x plus + The number of tickets for large rides 5 y Is less than or equal to ≤ Small rides 3 tickets 60 60

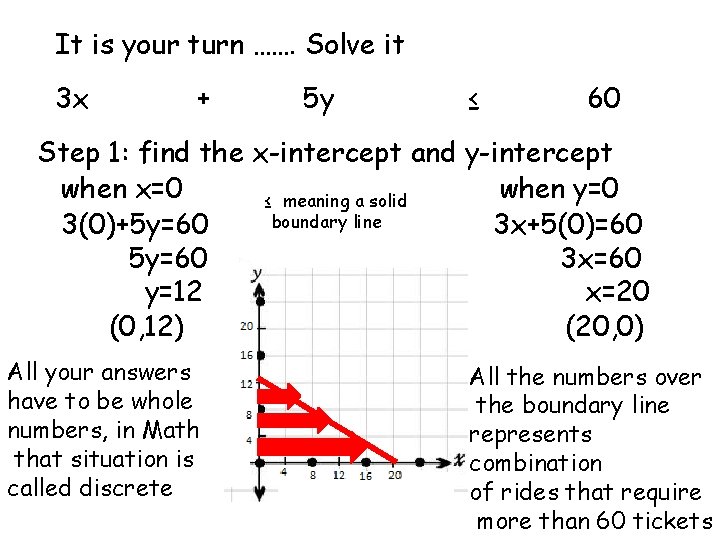
It is your turn ……. Solve it 3 x + 5 y ≤ 60 Step 1: find the x-intercept and y-intercept when x=0 when y=0 ≤ meaning a solid boundary line 3(0)+5 y=60 3 x+5(0)=60 5 y=60 3 x=60 y=12 x=20 (0, 12) (20, 0) All your answers have to be whole numbers, in Math that situation is called discrete All the numbers over the boundary line represents combination of rides that require more than 60 tickets

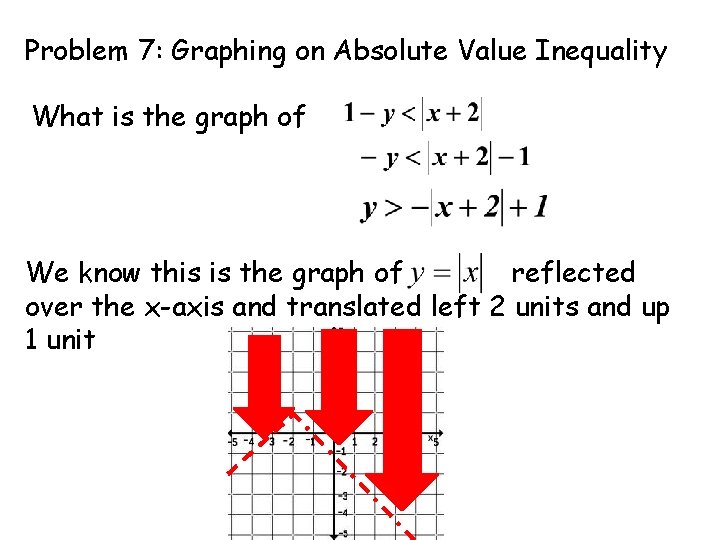
Problem 7: Graphing on Absolute Value Inequality What is the graph of We know this is the graph of reflected over the x-axis and translated left 2 units and up 1 unit

Your turn What is the graph of

Problem 8: Writing an inequality based on a graph What inequality does this graph represent? The vertex is translated 2 units to the right and 1 up, (2, 1)so the boundary is the graph of now is a dashed line

Classwork odd Homework even