Absolute Metabolite Concentrations on Brain Tissue by Gaussian

Absolute Metabolite Concentrations on Brain Tissue by Gaussian and Lorentzian Functions Amarjeet Bhullar Bimonthly Meeting on Dec. 5, 2008

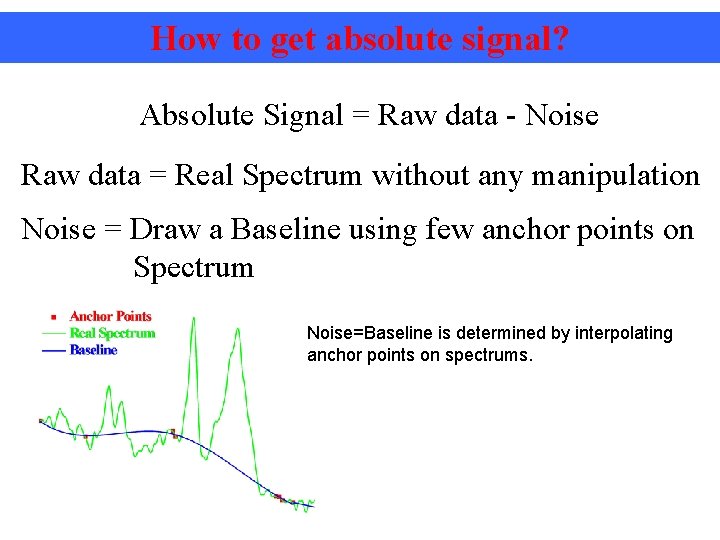
How to get absolute signal? Absolute Signal = Raw data - Noise Raw data = Real Spectrum without any manipulation Noise = Draw a Baseline using few anchor points on Spectrum Noise=Baseline is determined by interpolating anchor points on spectrums.

Absolute Metabolite Concentrations • Create baseline using few anchor points on spectrum. • Find metabolite peaks. • Fit Mathematical function on metabolite peaks. • Integrate peaks between the limits to calculate absolute metabolite concentrations.

Mathematical Model: Gaussian Function

Integral of Gaussian Function : Error Function Numerically: Codes developed in C and Mathematica 6. 0

Integral of Gaussian Function : Gamma Function

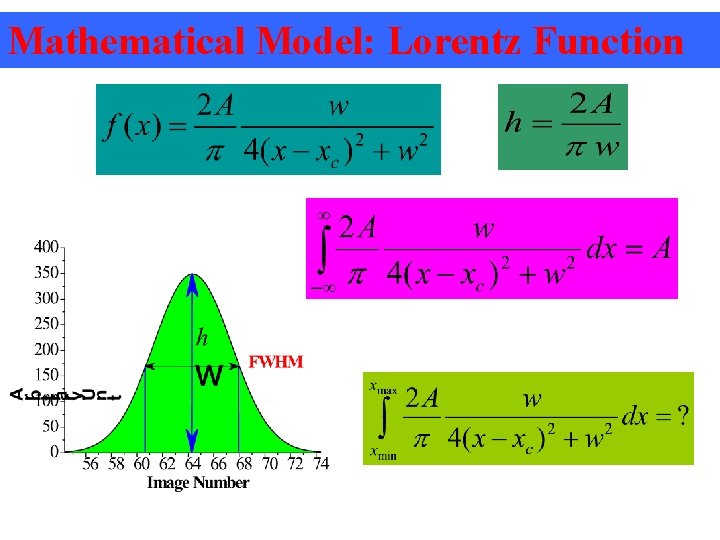
Mathematical Model: Lorentz Function

Integral of Lorentzian Function : Arc. Tan

Difference Between Lorentzian and Gaussian Function

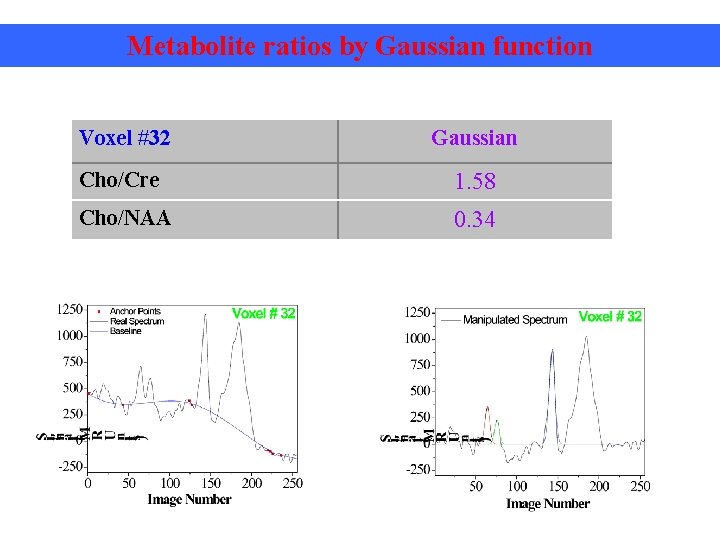
Metabolite ratios by Gaussian function Voxel #32 Gaussian Cho/Cre 1. 58 Cho/NAA 0. 34

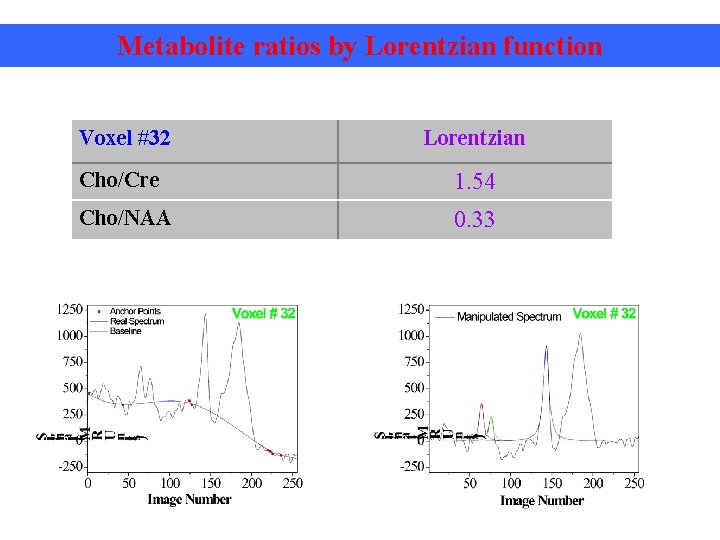
Metabolite ratios by Lorentzian function Voxel #32 Lorentzian Cho/Cre 1. 54 Cho/NAA 0. 33

Conclusion: Voxel #32 Gaussian Lorentzian Average Cho/Cre 1. 58 1. 54 1. 55 Cho/NAA 0. 34 0. 33 Both mathematical models have produced the same ratios. Suggestions are welcome