About the Use of Correlations in Component Based

About the Use of Correlations in Component Based Frameworks Georg Jung jung@cis. ksu. edu Department of Computing and Information Sciences Kansas State University
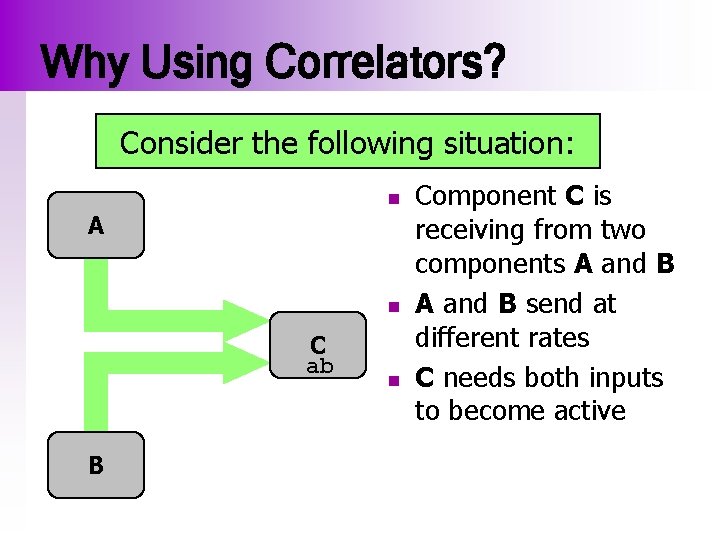
Why Using Correlators? Consider the following situation: n A a n C ab b B n Component C is receiving from two components A and B send at different rates C needs both inputs to become active
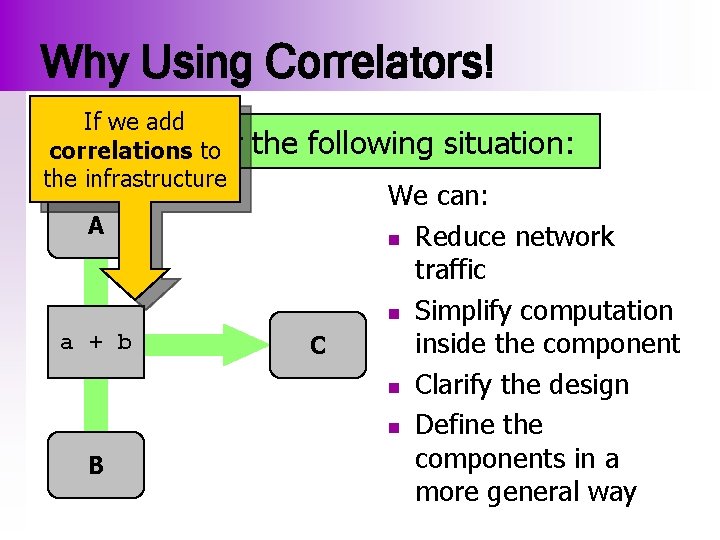
Why Using Correlators! If we add Consider correlations to the infrastructure the following situation: A a a +ab b b B C We can: n Reduce network traffic n Simplify computation inside the component n Clarify the design n Define the components in a more general way
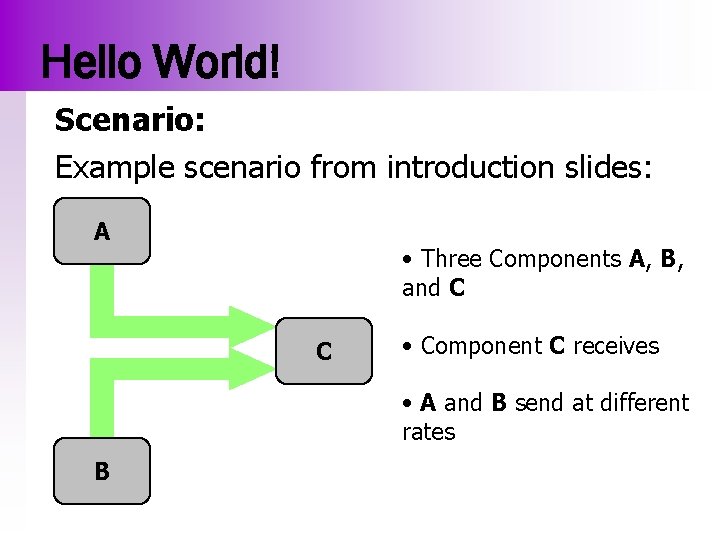
Hello World! Scenario: Example scenario from introduction slides: A • Three Components A, B, and C C • Component C receives • A and B send at different rates B

Hello World! φC correlation Hello. World (φA a, φB b)Head a + b Filter { Transformer case true: push new φC { x : = a. data, y : = b. data } }
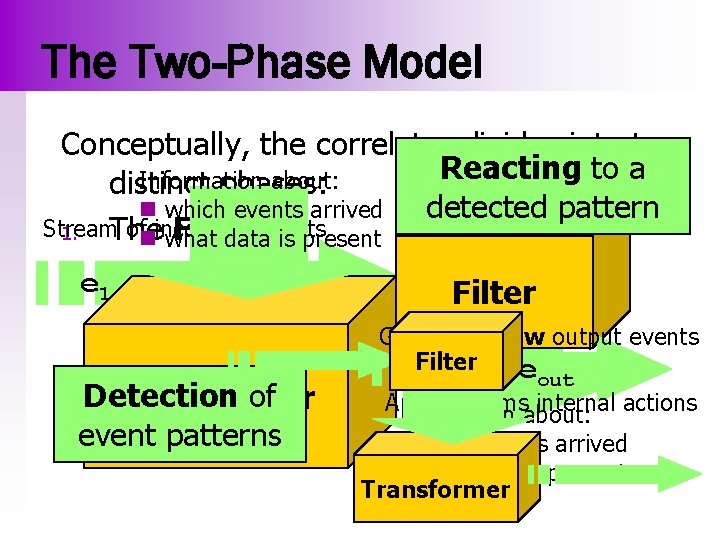
The Two-Phase Model Conceptually, the correlator divides into two Reacting to a Information about: distinct phases: detected pattern n which events arrived Stream ofnincoming events 1. The Filter what data is present 2. e The Transformer e e 1 e 2 1 3 Filter Detection of Transformer event patterns Generates new output events Filter e e out And performsabout: internal actions Information n which events arrived n what data is present Transformer

Back to “Hello World!” φC correlation Hello. World (φA a, φB b) a + In b this simple example { the transformer does a type conversion! case true: push new φC { x : = a. data, y : = b. data } }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems

Race Condition Scenario: Components A and B carry out a task and deliver the results to C. Component C expects the results to come in first from A, then from B. The resulting race condition between A and C can be caught with a correlator.

Race Condition Solution: φdata correlation Catch. Racing (φdata a, φdata b) a + b { case true: push a; push b; }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems

Most Recent / Earliest Scenario: A component C receives from A and B. a + b when both events arrive, C wants the most recent (earliest) of both forwarded. We change the filter expression to: la: (a ; b) | lb: (b ; a)

Most Recent / Earliest φData correlation First (φData a; φData b) la: (a; b) | lb: (b; a) { case la: push a; case lb: push b; }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems

Double Match Consider the following filter expression: (a + b) | (a + c) And the following streams: a b a a c c … matches: a + b a c a b b a … matches: a + c c b b c a a … matches: a + b and a + c

Double Match l 1: (a + b) | l 2: (a + c) Adding Labels to the expression (a + b) | (a + c)

Double Match l 1: (a + b) | l 2: (a + c) Transformer 1: Send a general notification { } case true: push new φnote {};

Double Match l 1: (a + b) | l 2: (a + c) Transformer 2: Send two outputs { case l 1: push b; case l 2: push c; }

Double Match l 1: (a + b) | l 2: (a + c) Transformer 3: Send one output, with priority on b if present. { case l 1: push b; case l 2 & !l 1: push c; }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems

Interleaving Event We consider three subexpressions x 1, x 2, x 3. x 2 shall not interleave between x 1 and x 3. x 1 ; (l 2: (x 2 ; x 3) | l 3: x 3) φ correlation Interleaving (. . . ) x 1 ; (l 2: (x 2 ; x 3) | l 3: x 3) { case l 2: push some error event; case l 3 & !l 2: push some success event; }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems
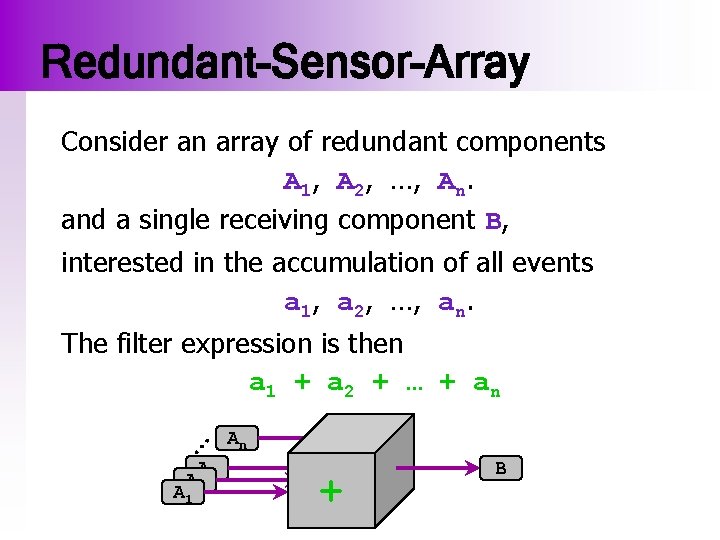
Redundant-Sensor-Array Consider an array of redundant components A 1, A 2, …, An. and a single receiving component B, interested in the accumulation of all events a 1, a 2, …, an. … The filter expression is then a 1 + a 2 + … + a n A A 2 3 A 1 An + B

Redundant-Sensor-Array a 1 + a 2 + … + a n In a component system some components can be temporarily unavailable! … If one component does not send anymore the whole pattern is never satisfied! A A 2 3 A 1 An + B
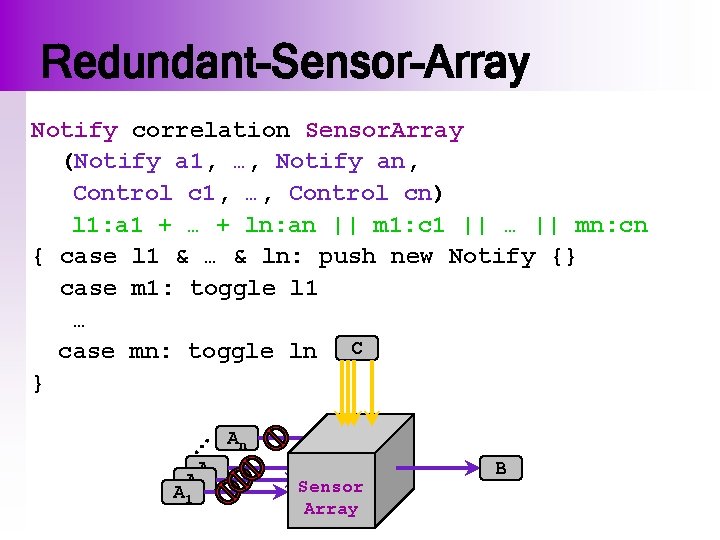
Redundant-Sensor-Array … Notify correlation Sensor. Array (Notify a 1, …, Notify an, Control c 1, …, Control cn) l 1: a 1 + … + ln: an || m 1: c 1 || … || mn: cn { case l 1 & … & ln: push new Notify {} case m 1: toggle l 1 … case mn: toggle ln C } A A 2 3 A 1 An Sensor Array B

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems

Mode-Awareness Scenario: This scenario generalizes the previous. Instead of single devices to switch on or off, we have a several modes to chose from. The same mechanism is used to switch between modes as previously to switch the different devices on and off.

Mode Awareness n filter expressions, labeled with n labels: m 1: e 1 || … || mn: en n labeled control events: l 1: c 1 || … || ln: cn

Mode Awareness φout correlation Modal 3 (φc c 1, φ c c 2, φ c c 3, arguments for ei…) m 1: e 1 || m 2: e 2 || m 3: e 3 || l 1: c 1 || l 2: c 2 || l 3: c 3 { abort (m 2, m 3); clauses for e 1, e 2, e 3… case l 1: revive (m 1); abort (m 2, m 3); case l 2: revive (m 2); abort (m 1, m 3); case l 3: revive (m 3); abort (m 1, m 2); }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to handle a double match n How to catch interleaving events n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems

Periodic Checks of Aperiodic Events Scenario: We introduce a periodic supervisor component into an aperiodic system. Whenever a clock-tick occurs, a sample is collected and sent to the supervisor.

Periodic Checks of Aperiodic Events φsample correlation Periodic. Chck (φtimer t, φa a, φb b, φc c) t ; (l 1: (a + b + c) | l 2: t) { case l 1: push new φsample{d 1 : = a. data, d 2 : = b. data, d 3 : = c. data } case l 2: push some error event (missed sample); }

Examples This presentation will include: n How to prevent a race condition n How to chose the most recent/earliest in a sequence n How to These handle are a double match our examples. n How to catch interleaving events Feel free to add your own… n How to deal with redundant-device-components n How to introduce mode-dependent behavior n How to bridge the gap between periodic and aperiodic systems
- Slides: 33