abdulhadisutrisno Yang kuingin Standar kompetensi Kompetensi dasar Indikator

abdulhadisutrisno
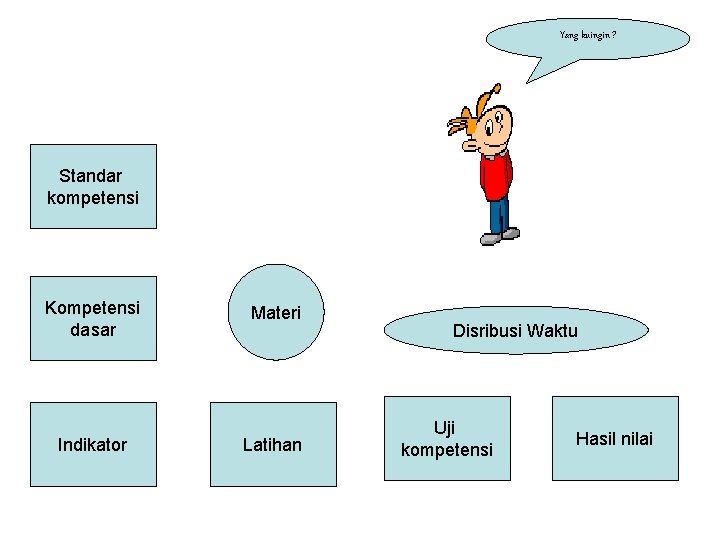
Yang kuingin ? Standar kompetensi Kompetensi dasar Indikator Materi Latihan Disribusi Waktu Uji kompetensi Hasil nilai

Standar Kompetensi : 3. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah

Kompetensi Dasar : 3. 3 Menggunakan sifat dan aturan turunan dalam perhitunganan turunan fungsi aljabar

INDIKATOR 1. Siswa dapat menggunakan rumus turunan fungsi konstan 2. Siswa dapat menggunakan rumus turunan fungsi identitas 3. Siswa dapat menggunakan rumus turunan fungsi pangkat 4. Siswa dapat menggunakan rumus turunan jumlah fungsi 5. Siswa dapat menggunakan rumus turunan selisih fungsi 6. Siswa dapat menggunakan rumus turunan perkalian fungsi 7. Siswa dapat menggunakan rumus turunan pembagian fungsi

RENCANA PEMBELAJARAN (LESSON PLAN) Nama : Abdul Hadi Sutrisno Sekolah : SMA NEGERI 1 BANJARMASIN Mata Pelajaran : Matematika Kompetensi Dasar : 3. 3 Menggunakan sifat dan aturan turunan dalam perhitunganan turunan fungsi aljabar Indikator menggunakan rumus turunan fungsi dalam menyelesaikan perhitungan turunan fungsi aljabar :

Materi Pokok : Rumus Turunan Fungsi Kelas / Program/ Semester : XI / IPA/2 Sasaran Hasil Belajar : siswa dapat menggunakan rumus turunan fungsi dalam menyelesaikan perhitungan turunan fungsi aljabar Waktu : 2 x 45 menit Perangkat ICT/ Sumber yang digunakan : Hand-out, LKS, Buku Matematika, Lab. Computer, Lab. internet Koneksi internet dengan web broser yang sudah di install program Plug-In Flash, Java, Adobe, Maromedia Power Point XP
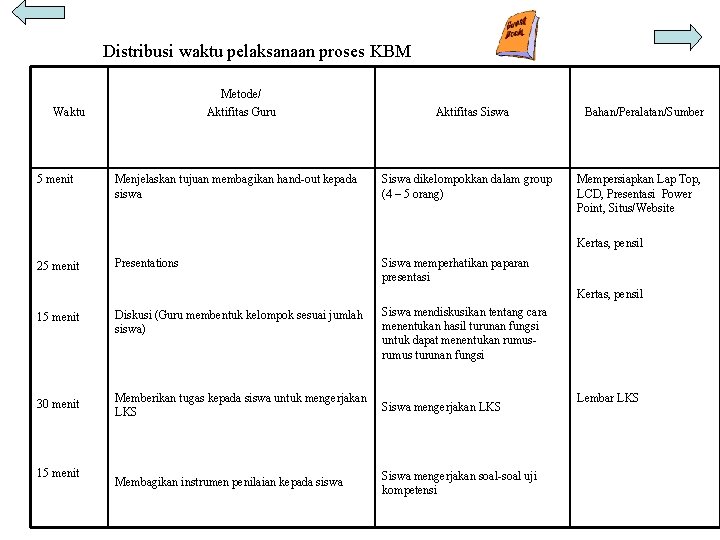
Distribusi waktu pelaksanaan proses KBM Metode/ Aktifitas Guru Waktu 5 menit Menjelaskan tujuan membagikan hand-out kepada siswa Aktifitas Siswa dikelompokkan dalam group (4 – 5 orang) Bahan/Peralatan/Sumber Mempersiapkan Lap Top, LCD, Presentasi Power Point, Situs/Website Kertas, pensil 25 menit Presentations Siswa memperhatikan paparan presentasi Kertas, pensil Siswa mendiskusikan tentang cara menentukan hasil turunan fungsi untuk dapat menentukan rumus turunan fungsi 15 menit Diskusi (Guru membentuk kelompok sesuai jumlah siswa) 30 menit Memberikan tugas kepada siswa untuk mengerjakan LKS Siswa mengerjakan LKS Membagikan instrumen penilaian kepada siswa Siswa mengerjakan soal-soal uji kompetensi 15 menit Lembar LKS

Teorema Umum. Turunan Fungsi • Teorema 1 : Turunan fungsi konstan Jika f(x)=k dengan k konstanta, maka f ‘(x)=0 • Teorema 2 : Turunan fungsi identitas Jika f(x)=x , maka f ‘(x)=0 • Teorema 3 : Turunan fungsi pangkat Jika f(x)= , maka f ‘(x)=

• Teorema 4 : Turunan Hasilkali Konstanta dengan Fungsi Jika f(x) suatu fungsi dan c suatu konstanta yang didefinisikan oleh g(x)=c. f(x) dan f’(x) ada maka g’(x)=c. f’(x) • Teorema 5 : Turunan Jumlah Fungsi Jika u dan v adalah fungsi-fungsi dari x yang dapat diturunkan dan f(x) =u(x) + v(x) maka f ‘(x) = u’(x) + v’(x)

• Teorema 6 : Turunan Selisih Fungsi Jika u dan v adalah fungsi-fungsi dari x yang dapat diturunkan dan f(x) =u(x) - v(x) maka f ‘(x) = u’(x) - v’(x) • Teorema 7 : Turunan Perkalian Fungsi Jika u dan v adalah fungsi-fungsi dari x yang dapat diturunkan dan f(x) =u(x). v(x) maka f ‘(x) = u’(x). V(x) + u(x). v’(x)

• Teorema 8 : Turunan Pembagian Fungsi Jika u dan v adalah fungsi-fungsi dari x yang dapat diturunkan dan f(x) = maka f ‘(x) =

Contoh 1 Turunan fungsi adalah Contoh 2 Turunan fungsi adalah Contoh 3 Turunan fungsi adalah

Latihan : Tentukan hasil turunan fungsi-fungsi nomor 1 sampai 7

UJI KOMPETENSI Tentukan turunan fungsi-fungsi pada soal nomor 1 sampai 10


LATIHAN KERJA SISWA


- Slides: 19