ABC Logic Synthesis basics ECE 667 Synthesis and

ABC Logic Synthesis basics ECE 667 Synthesis and Verification of Digital Systems Spring 2011 Archana Rengaraj Electrical and Computer Engineering

Overview § Introduction • Previous synthesis methods § ABC synthesis § And-Inverter Graphs (AIG) representation • AIG canonicity and redundancy • AIG construction § NPN equivalence § AIG transformations • Rewriting • ABC commands § Summary Electrical and Computer Engineering 2

Introduction § Synthesis of a design • Conversion of abstract form of desired circuit behavior into a form of logic gates § Processing combinational logic before technology mapping • technology independent optimization § Technology dependent optimization • Synthesis targeting ASICs and FPGAs Electrical and Computer Engineering 3

SIS Synthesis § Previous systems for logic synthesis and optimization: SIS, VIS – Verification Interacting with Synthesis, MVSIS - Multi valued SIS § Drawbacks of these systems • Cannot integrate technology mapping and retiming • Inefficient for large circuits • Areas of improvement • quality and runtime of synthesis and verification Electrical and Computer Engineering 4

SIS Synthesis algorithm § Traditional combinational synthesis steps • • sweep – removing redundant nodes eliminate, resubstitute - finding better logic boundaries fast_extract – detect shared logic simplify, full_simplify – optimization of nodes Electrical and Computer Engineering 5

ABC synthesis § Representing logic in terms of And Inverter Graphs (AIG) § Difference from SIS systems • simple data structure: Two-input ANDs and Inverters • Transformation of network done by rewriting AIGs § Advantages: scalable, faster, uniformity in computation, better quality after technology mapping Electrical and Computer Engineering 6

ABC applications § synthesis and verification § combinational and sequential synthesis § combinational and sequential equivalence checking Electrical and Computer Engineering 7

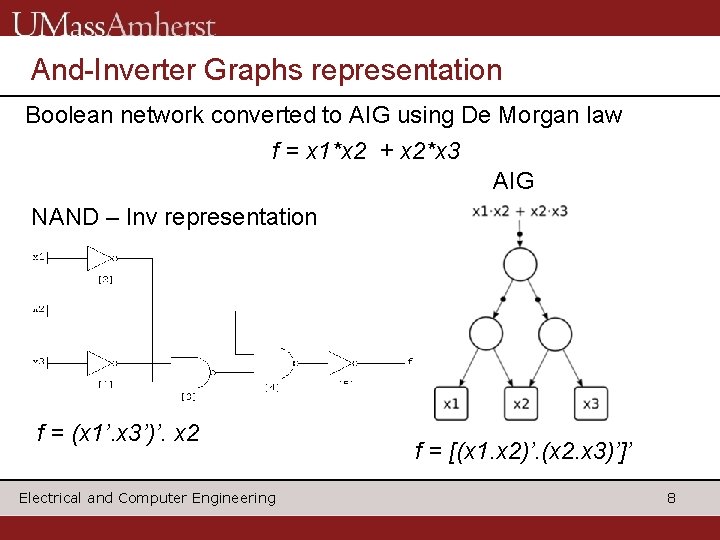
And-Inverter Graphs representation Boolean network converted to AIG using De Morgan law f = x 1*x 2 + x 2*x 3 AIG NAND – Inv representation f = (x 1’. x 3’)’. x 2 Electrical and Computer Engineering f = [(x 1. x 2)’. (x 2. x 3)’]’ 8

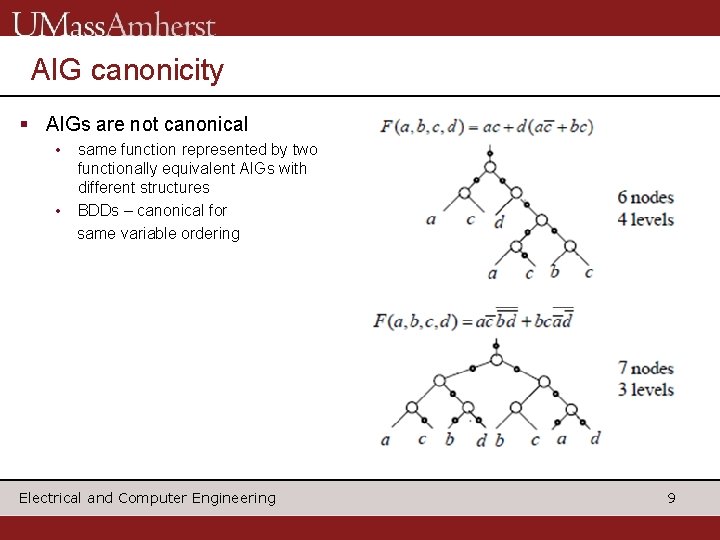
AIG canonicity § AIGs are not canonical • • same function represented by two functionally equivalent AIGs with different structures BDDs – canonical for same variable ordering Electrical and Computer Engineering 9

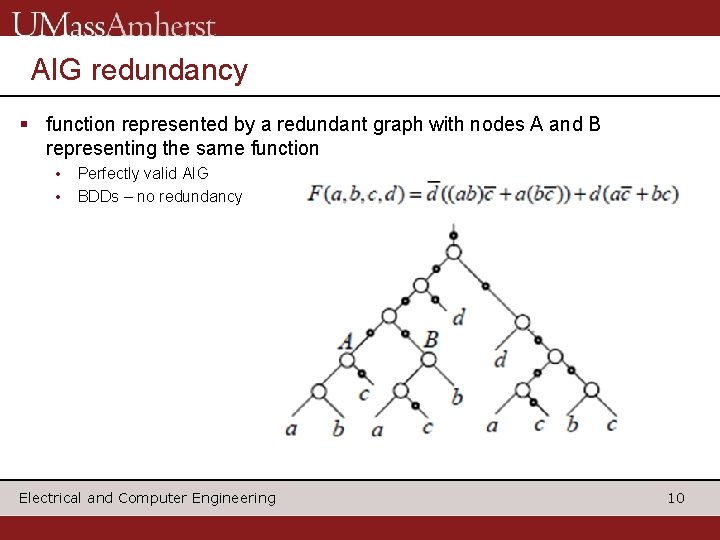
AIG redundancy § function represented by a redundant graph with nodes A and B representing the same function • • Perfectly valid AIG BDDs – no redundancy Electrical and Computer Engineering 10

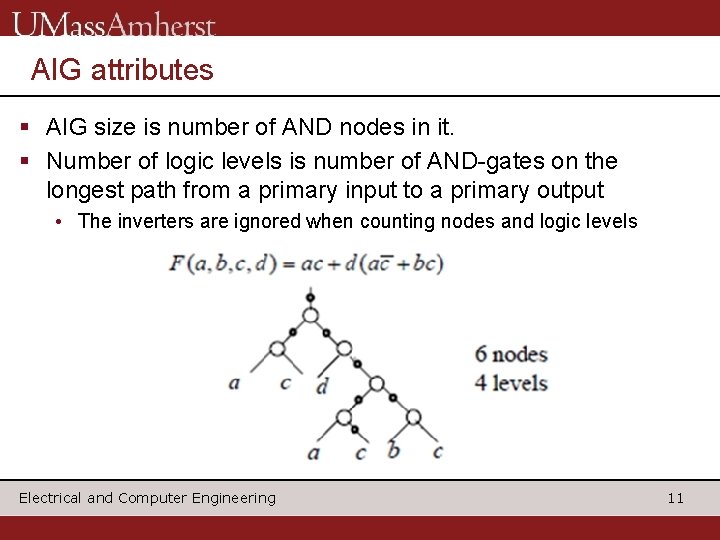
AIG attributes § AIG size is number of AND nodes in it. § Number of logic levels is number of AND-gates on the longest path from a primary input to a primary output • The inverters are ignored when counting nodes and logic levels Electrical and Computer Engineering 11

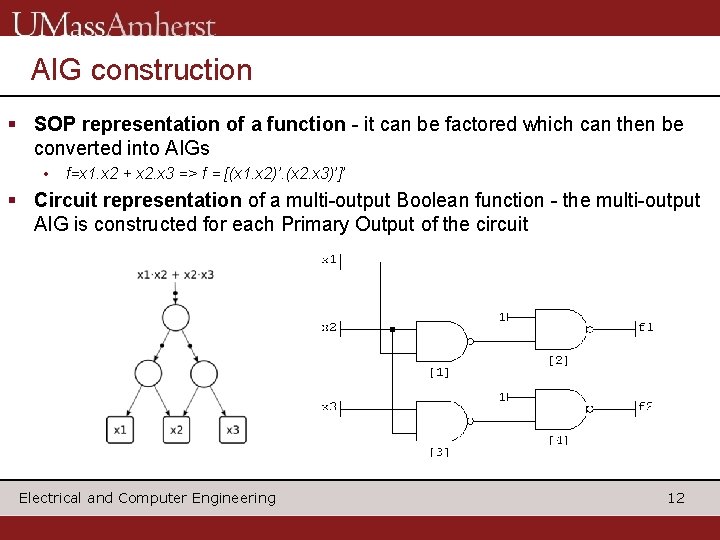
AIG construction § SOP representation of a function - it can be factored which can then be converted into AIGs • f=x 1. x 2 + x 2. x 3 => f = [(x 1. x 2)’. (x 2. x 3)’]’ § Circuit representation of a multi-output Boolean function - the multi-output AIG is constructed for each Primary Output of the circuit Electrical and Computer Engineering 12

Definitions § Cut • set of nodes of network, called leaves • each path from PIs to n passes through at least one leaf § K-feasible cut • if the number of leaves does not exceed K § Cut function of an AIG node n, fn(x) • A boolean function of the logic cone rooted in node n and expressed in terms of the cut leaves of the AIG. § Structural hashing (command: strash) • during AIG construction, no two AND gates should have identical pairs of incoming edges • to detect and merge isomorphic circuit structures • AIG not canonical, it contains sub-graphs, which are canonical Electrical and Computer Engineering 13

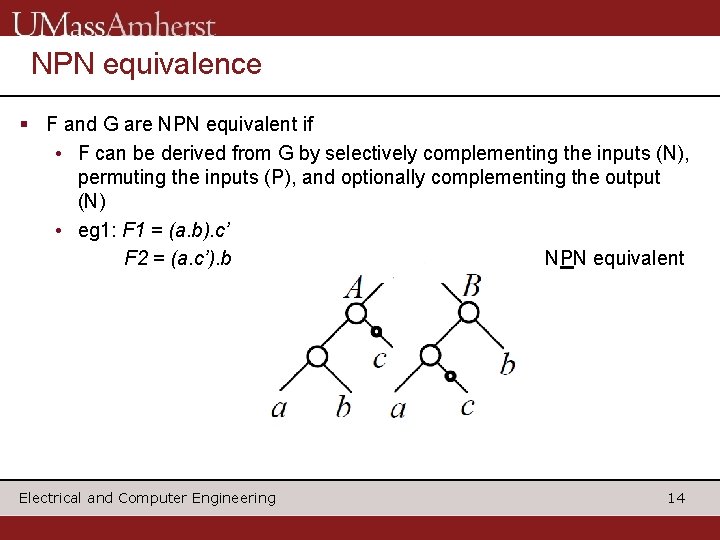
NPN equivalence § F and G are NPN equivalent if • F can be derived from G by selectively complementing the inputs (N), permuting the inputs (P), and optionally complementing the output (N) • eg 1: F 1 = (a. b). c’ F 2 = (a. c’). b NPN equivalent Electrical and Computer Engineering 14

NPN equivalence contd. • eg 2: f 1 = x 1 x 2’x 3 + x 2 x 3’ + x 4 f 2 = x 1’x 2’x 3 + x 4 f 3 = x 1 x 2 x 3 + x 2’x 3’ + x 4’ NPN equivalent f 1 and f 2 not N-equivalent f 1 and f 3 are N-equivalent - f 1 and f 3 can be transformed into each other by complementing x 2, x 4 § Representatives of each class can be transformed into each other by complementing their inputs § But no transformation between representatives of different classes Electrical and Computer Engineering 15

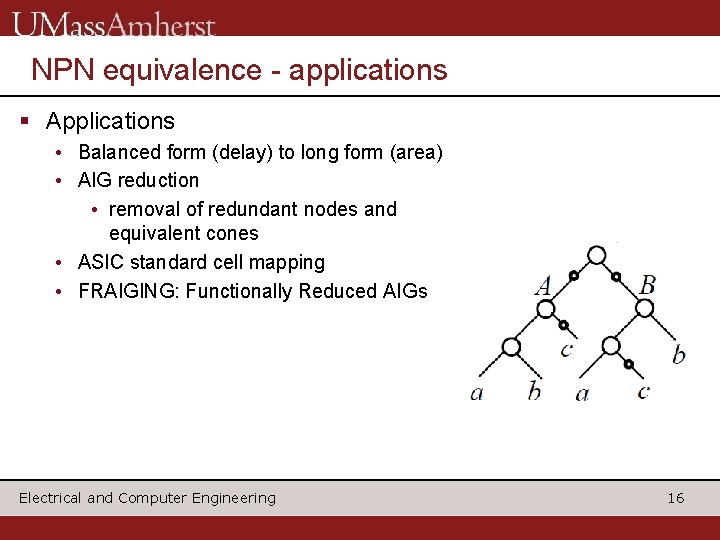
NPN equivalence - applications § Applications • Balanced form (delay) to long form (area) • AIG reduction • removal of redundant nodes and equivalent cones • ASIC standard cell mapping • FRAIGING: Functionally Reduced AIGs Electrical and Computer Engineering 16

Overview § Introduction • Previous synthesis methods § ABC synthesis § And-Inverter Graphs (AIG) representation • AIG canonicity and redundancy • AIG construction § NPN equivalence § AIG transformations • Rewriting • ABC commands § Summary Electrical and Computer Engineering 17

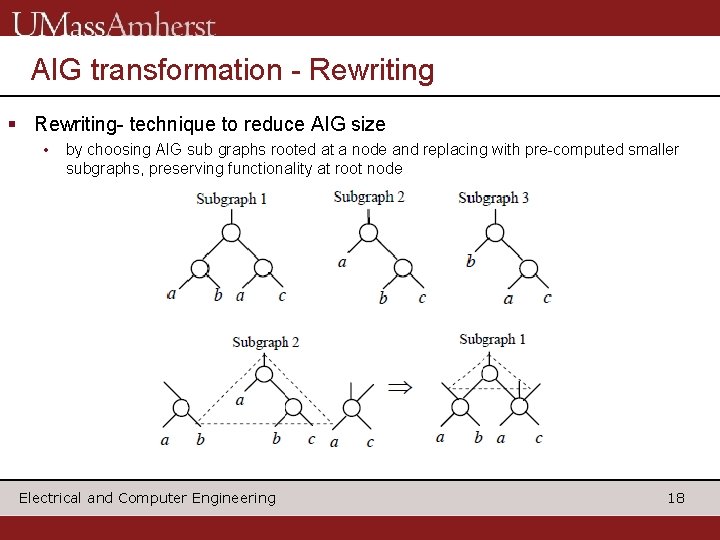
AIG transformation - Rewriting § Rewriting- technique to reduce AIG size • by choosing AIG sub graphs rooted at a node and replacing with pre-computed smaller subgraphs, preserving functionality at root node Electrical and Computer Engineering 18

AIG rewriting basics § Selectively collapse, refactor and balance § Collapse – elimination • f = (g). c’ • g = a. b => f = (a. b). c’ Refactor • iterative collapsing and refactoring of logic cones in the AIG to reduce the number of AIG nodes and number of logic levels § Balance • creates a second AIG from an input AIG, having minimum delay (number of logic levels) § Synthesis based on AIGs • Alternating DAG aware AIG rewriting and algebraic AIG balancing Electrical and Computer Engineering 19

AIG rewriting algorithm Electrical and Computer Engineering 20

AIG rewriting variation Refactoring § compute one large cut for each AIG node § replace AIG structure of the cut by a factored form of the cut function § Accept change if there is a decrease or no change in number of nodes Cost function § AIG rewriting - total number of AIG nodes and the maximum number of AIG levels § SIS methods - total number of literals in the factored forms Electrical and Computer Engineering 21

AIG rewriting - advantages § Not much hand-tuning and trial and error § Complexity of logic given by AIG nodes or levels § An implementation of synthesis flow takes person-weeks • Orders of magnitude faster § AIG rewriting leads to better quality than those offered by MVSIS and SIS • AIG rewriting is local, fast, can be applied many times • No longer local rewriting – better quality § Scalability - applicable to large examples Electrical and Computer Engineering 22

AIG rewriting - applications § Applications • • formal verification design complexity estimation equivalence checking hardware emulation Electrical and Computer Engineering 23

ABC rewriting script § resyn 2 - rewriting script § Performs ten passes on the network • • • b – Balance rw – rewrite rf – refactor b rw rwz – rewrite with switch enabling zero-cost replacements b rfz - refactor with switch enabling zero-cost replacements rwz b Electrical and Computer Engineering 24

ABC commands – logic synthesis § resyn, resyn 2, and resyn 2 rs – logic synthesis scripts § strash • Structural hashing - standard alias st § renode • recreates node boundaries in AIG by using command renode • standard alias ren Electrical and Computer Engineering 25

ABC commands contd. § share and sharedsd • scripts for logic sharing extraction § rr • Performs redundancy removal for AIGs Electrical and Computer Engineering 26

Summary § Synthesis done using ABC represents network in terms of a simpler data structure - AIGs § Performs combinational synthesis, mapping, and verification § faster § Better quality of results after technology mapping § Scalable for large designs Electrical and Computer Engineering 27

References [1] Alan Mishchenko , Satrajit Chatterjee, Robert Brayton, “DAG-Aware AIG Rewriting”, DAC 2006, July 24– 28, 2006, San Francisco, California, USA. [2] Alan Mishchenko, “A New Enhanced Approach to Technology Mapping”. [3] Alan Mishchenko, Satrajit Chatterjee, Roland Jiang, Robert Brayton, “FRAIGs: A Unifying Representation for Logic Synthesis and Verification”. Electrical and Computer Engineering 28

Thank you Electrical and Computer Engineering 29