AB Unit 6 B 49 Steps for Eulers

AB Unit 6 B

49. Steps for Euler’s Method ● Approximation is based on tangent line ● ynext = yold + dy/dx(△x) ● Identify the step size, derivative, and initial value ● Step size can be negative

Example Problem Given dy/dx = x + 2 and y is 3 when x is 0. Use Euler’s method with step size 1/2 Find the value of y when x is 1.

50. Relationship Between Direct Variation and Exponential Decay ● If problems states rate of change is proportional to amount. ○ dy/dx = ky ● If problems states rate of change is inversely proportional to amount ○ dy/dx = k/y

Example Problem The rate of change of y is proportional to y. When t = 0, y = 2. When t = 2, y = 4. What is y when t = 3?

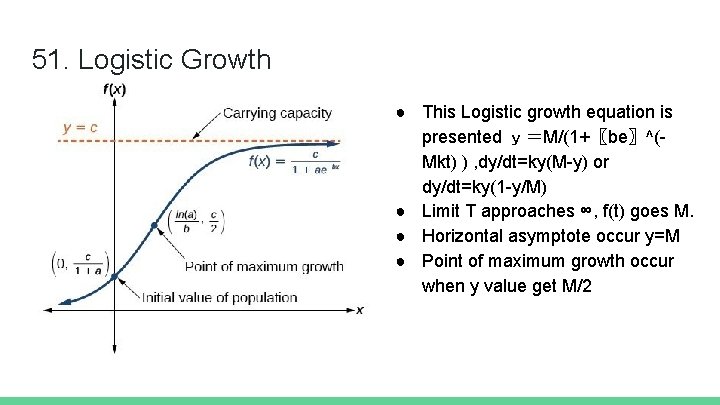
51. Logistic Growth ● This Logistic growth equation is presented ｙ＝M/(1+〖be〗^(Mkt) ) , dy/dt=ky(M-y) or dy/dt=ky(1 -y/M) ● Limit T approaches ∞, f(t) goes M. ● Horizontal asymptote occur y=M ● Point of maximum growth occur when y value get M/2

Example problem The number N(t)N, left parenthesis, t, right parenthesis of people who have adopted a certain fashion style after ttt months satisfies the logistic differential equation: d. N/dt=N(0. 1 -N/700000) Initially, there were 3000 people who had adopted the style. What is the number of people who have adopted the style when it's growing the fastest? Solution 1. Find d. N/dt=0 2. Take average for N The answer is 35000

Play Quizizz! https: //quizizz. com/admin/quiz/start_new/5 cab 3 db 28 af 501001 a 7 cd 2 de

Free Response

Answers www. umath 2. com/Calc. BC/docs/chap 6/BCEuler. Slope. Field. Diff. Eq. pdf