AASTMT Engineering and Technology College CC 215 DATA

AASTMT Engineering and Technology College CC 215 DATA STRUCTURES MORE ABOUT STACK APPLICATIONS Lecture 6 Dr. Manal Helal - Fall 2014 1

Quick Recap 2 Stacks are linear lists. All deletions and insertions occur at one end of the stack known as the TOP. Data going into the stack first, leaves out last. Stacks are also known as LIFO data structures (Last-In, First-Out).

Basic Stack Operations 3 push – Adds an item to the top of a stack. pop – Removes an item from the top of the stack and returns it to the user. stack top (top, peek) – Copies the top item of the stack and returns it to the user; the item is not removed, hence the stack is not altered.

Additional Notes 4 Stacks structures are usually implemented using arrays or linked lists. For both implementations, the running time is O(n). We will be examining common Stack Applications.

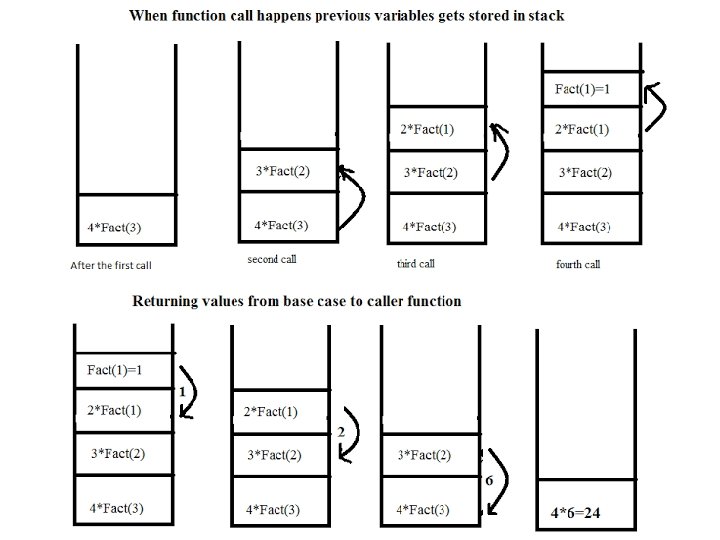
Uses of Stacks 5 The runtime stack used by a process (running program) to keep track of methods in progress Undo, redo, back, forward

Search Backtracking 7 Stacks can be used to backtrack to achieve certain goals. Usually, we set up backtrack tokens to indicate a backtrack opportunity.

Stack Applications 8 Reversing Data: We can use stacks to reverse data. (example: files, strings) Very useful for finding palindromes. Consider the following pseudocode: 1) read (data) 2) loop (data not EOF and stack not full) 1) push (data) 2) read (data) 3) Loop (while stack not. Empty) 1) pop (data) 2) print (data)

Stack Applications 9 Converting Decimal to Binary: Consider the following pseudocode Read (number) 2) Loop (number > 0) 1) digit = number modulo 2 2) print (digit) 3) number = number / 2 // from Data Structures by Gilbert and Forouzan 1) The problem with this code is that it will print the binary number backwards. (ex: 19 becomes 11001000 instead of 00010011. ) To remedy this problem, instead of printing the digit right away, we can push it onto the stack. Then after the number is done being converted, we pop the digit out of the stack and print it.

Balanced Symbol Checking 10 In processing programs and working with computer languages there are many instances when symbols must be balanced {}, [], () A stack is useful for checking symbol balance. When a closing symbol is found it must match the most recent opening symbol of the same type. Applicable to checking html and xml tags!

11 Algorithm for Balanced Symbol Checking Make an empty stack read symbols until end of file if the symbol is an opening symbol push it onto the stack if it is a closing symbol do the following if the stack is empty report an error otherwise pop the stack. If the symbol popped does not match the closing symbol report an error At the end of the file if the stack is not empty report an error

Algorithm in practice 12 list[i] = 3 * ( 44 - method( foo( list[ 2 * (i + 1) + foo( list[i - 1] ) ) / 2 * ) - list[ method(list[0])]; Complications Processing a file when is it not an error to have non matching symbols? Tokenization: the process of scanning an input stream. Each independent chunk is a token. Tokens may be made up of 1 or more characters

Mathematical Calculations 13 What does 3 + 2 * 4 equal? 2 * 4 + 3? 3 * 2 + 4? The precedence of operators affects the order of operations. A mathematical expression cannot simply be evaluated left to right. A challenge when evaluating a program. Lexical analysis is the process of interpreting a program. What about 1 - 2 - 4 ^ 5 * 3 * 6 / 7 ^ 2 ^ 3

Infix and Postfix Expressions 14 The way we are use to writing expressions is known as infix notation Postfix expression does not require any precedence rules 3 2 * 1 + is postfix of 3 * 2 + 1 evaluate the following postfix expressions and write out a corresponding infix expression: 2324*+* 12 -32^3*6/+ Stacks 1234^*+ 25^1 CS 314

Clicker Question 2 15 What does the following postfix expression evaluate to? 632+* A. 18 B. 36 C. 24 D. 11 E. 30 8 Stacks CS 314

Stack Applications 16 Postponement: Evaluating arithmetic expressions. Prefix: + a b Infix: a + b (what we use in grammar school) Postfix: a b + In high level languages, infix notation cannot be used to evaluate expressions. We must analyze the expression to determine the order in which we evaluate it. A common technique is to convert a infix notation into postfix notation, then evaluating it.

Infix to Postfix Conversion 17 Rules: Operands immediately go directly to output Operators are pushed into the stack (including parenthesis) - compare current operator o 1 to stack top operator o 2 - - while ((o 1<= o 2 and o 1 is left-associative) or (o 1< o 2 and o 1 is right associative)) - Pop (o 2) and check the next o 2 to remain in the loop or exit Push (o 1); i. e. push o 1 when its precedence is higher than o 2 generally, otherwise, pop o 2 taking into consideration the associativity rules shown above. Priority 1: * / ^ Priority 0: + - Open parenthesis are always pushed on the stack. If we encounter a closing parenthesis, pop the stack and print the operators until you see a left parenthesis. Do not output parenthesis.

Infix to Postfix Example #1 18 A + B * C - D / E (general example) Infix Stack(bot->top) a) A + B * C - D / E b) + B * C - D / E c) B * C - D / E + d) *C-D/E + e) C-D/E +* f) -D/E +* g) D/E h) /E i) E -/ j) k) Postfix A A AB AB ABC*+D -/ ABC*+DE/-

Infix to Postfix Example #2 19 A / B ^ C - D (operator precedence example) Infix a) b) c) d) e) f) g) h) i) Stack(bot->top) A/B^C-D C-D -D D empty / / /^ /^ / empty - empty A A AB AB ABC^/ - j) k) Postfix empty ABC^/D-

Infix to Postfix Example #3 20 A * B - ( C + D ) + E (parenthesis example) Infix a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) Stack(bot->top) A*B-(C+D)+E -(C+D)+E D)+E-(+ )+E -(+ +E + E empty E + empty * * empty -( -( + empty Postfix empty A A AB AB* AB*CD AB*CD+AB*CD+-E+

Infix to Postfix Example #4 21 A-B+C Infix a) b) c) d) e) f) g) Stack(bot->top) A-B+C B+C +C C (left to right association) Postfix empty + + empty A A AB ABAB-C+

Infix to Postfix Example #5 22 A^B^C Infix a) b) c) d) e) f) g) Stack(bot->top) A^B^C B^C ^C C (right to left association) Postfix empty ^ ^ ^^ ^^ empty A A AB AB ABC^^

Evaluation of Postfix Expressions 23 Easy to do with a stack given a proper postfix expression: get the next token if it is an operand push it onto the stack else if it is an operator pop the stack for the right hand operand pop the stack for the left hand operand apply the operator to the two operands push the result onto the stack when the expression has been exhausted the result is the top (and only element) of the stack

Postfix Evaulation 24 Operand: push Operator: pop 2 operands, do the math, pop result back onto stack 123+* Postfix a) 123+* b) 23+* c) 3+* d) +* e) * f) Stack( bot -> top ) 5 1 12 123 1 5 // 5 from 2 + 3 // 5 from 1 * 5

25 Postfix Evaulation For Example #1 Infix: A + B * C - D / E Postfix: A B C * + D E / Values: A = 1, B = 2, C = 3, D = 4, E = 2 Postfix Stack( bot -> top ) a) 123*+42/empty b) 23*+42/1 c) 3*+42/12 d) *+42/123 e) +42/1 6 // 6 from 2 * 3 f) 42/7 // 7 from 1 + 6 g) 2/74 h) /742 i) 72 // 2 from 4 / 2 j) 5 // 5 from 7 - 2