AAE 556 Aeroelasticity The Pk flutter solution method

AAE 556 Aeroelasticity The P-k flutter solution method (also known as the “British” method) Purdue Aeroelasticity 1

The eigenvalue problem from the Lecture 33 Purdue Aeroelasticity 2

Genealogy of the V-g or “k” method i Equations of motion for harmonic response (next slide) – Forcing frequency and airspeeds are is known parameters – Reduced frequency k is determined from w and V – Equations are correct at all values of w and V. i Take away the harmonic applied forcing function – Equations are only true at the flutter point – We have an eigenvalue problem – Frequency and airspeed are unknowns, but we still need k to define the numbers to compute the elements of the eigenvalue problem – We invent ed Theodorsen’s method or V-g artificial damping to create an iterative approach to finding the flutter point Purdue Aeroelasticity 3

Go back to the original typical section equations of motion, restricted to steady-state harmonic response Purdue Aeroelasticity 4

The coefficients for the EOM’s Purdue Aeroelasticity 5

The eigenvalue problem Purdue Aeroelasticity 6

Another version of the eigenvalue problem with different coefficents Purdue Aeroelasticity 7

Definitions of terms for alternative set-up of eigenvalue equations for “k-method” Purdue Aeroelasticity 8

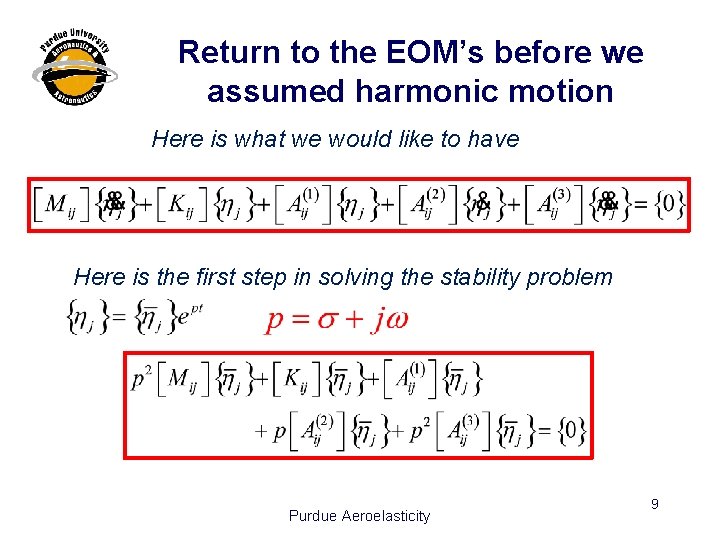
Return to the EOM’s before we assumed harmonic motion Here is what we would like to have Here is the first step in solving the stability problem Purdue Aeroelasticity 9

The p-k method will use the harmonic aero results to cast the stability problem in the following form …but first, some preliminaries Purdue Aeroelasticity 10

Revisit the original, harmonic EOM’s where the aero forces were still on the right hand side of the EOM’s and we hadn’t yet nondimensionalized h P Purdue Aeroelasticity 11

This lift expression looks strange; where is the dynamic pressure? Purdue Aeroelasticity 12

Writing aero force in different notation - more term definitions The Qij’s are complex numbers Purdue Aeroelasticity 13

Aero force in terms of the Qij’s Purdue Aeroelasticity 14

Focus first on the term Purdue Aeroelasticity 15

The second term Purdue Aeroelasticity 16

Let’s adopt notation from the controls community to help with our conversion Purdue Aeroelasticity 17

Continue working on the first term in the aero force expression The expression for A 11 reads Purdue Aeroelasticity 18

The term with the p in it looks like a damping term so let’s work on it Purdue Aeroelasticity 19

Finally, the exact expressions for each term are as follows Both terms are real numbers, there is no j here. Purdue Aeroelasticity 20

Aerodynamic moment expression Purdue Aeroelasticity 21

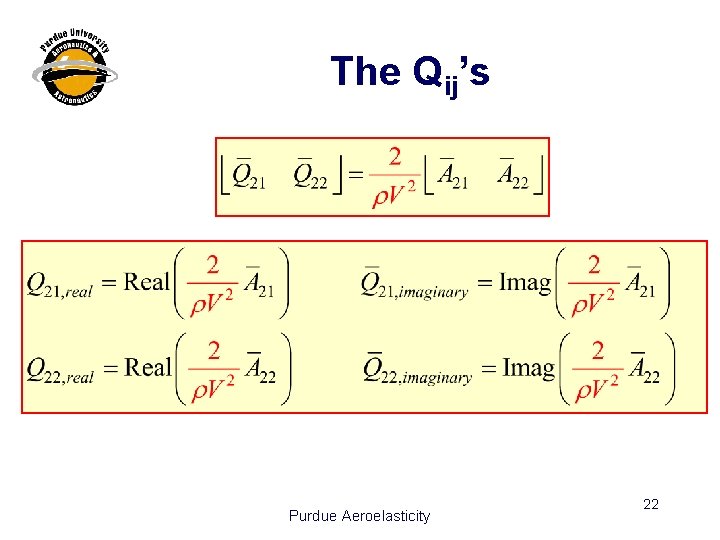
The Qij’s Purdue Aeroelasticity 22

The p-k process i Step 1 i Choose a value of k and compute all four complex aerodynamic coefficients – These are the complex Aij’s with the Theodorsen Circulation function in them – These will be a set of complex numbers, not algebraic expressions i Choose an air density (altitude) and airspeed (V) Purdue Aeroelasticity 23

Perform this computation Purdue Aeroelasticity 24

Compute the aerodynamic damping matrix, defined as Purdue Aeroelasticity 25

Take the results and insert them into an eigenvalue problem that reads as follows Purdue Aeroelasticity 26

Summary i i i Choose k=wb/V arbitrarily Choose altitude (r), and airspeed (V) Mach number is now known Compute AIC’s from Theodorsen formulas or others Compute aero matrices-B and Q matrices are real Purdue Aeroelasticity 27

Solving for the eigenvalues Convert the “p-k” equation to first-order state vector form State vector = Purdue Aeroelasticity 28

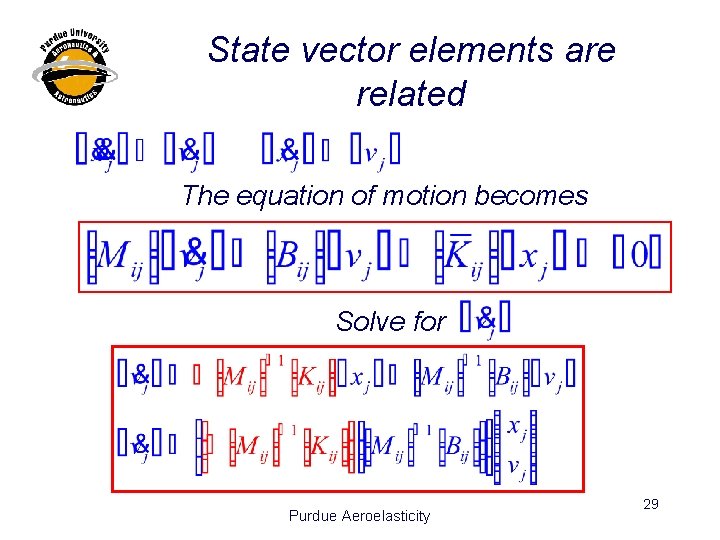
State vector elements are related The equation of motion becomes Solve for Purdue Aeroelasticity 29

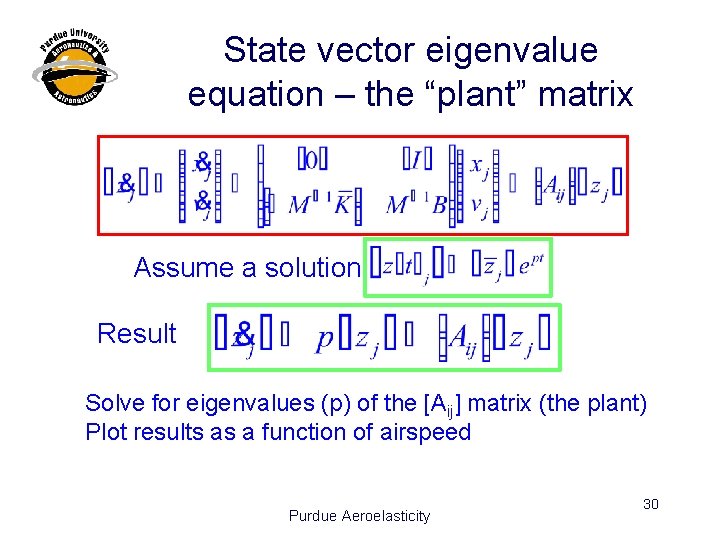
State vector eigenvalue equation – the “plant” matrix Assume a solution Result Solve for eigenvalues (p) of the [Aij] matrix (the plant) Plot results as a function of airspeed Purdue Aeroelasticity 30

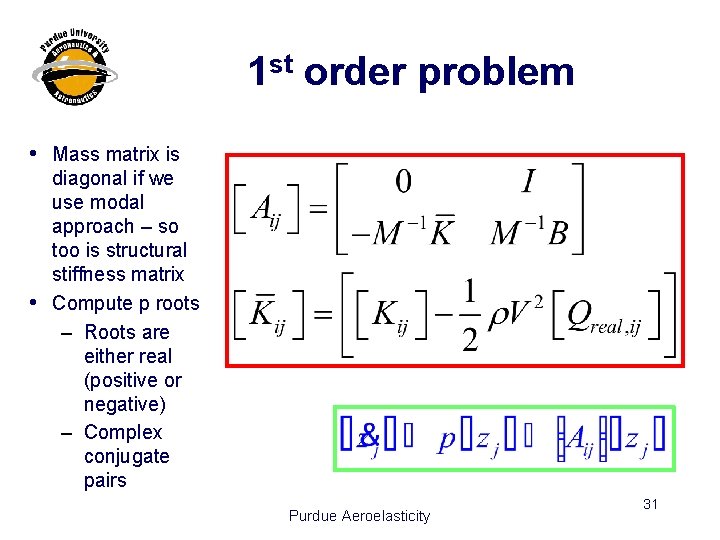
1 st order problem i i Mass matrix is diagonal if we use modal approach – so too is structural stiffness matrix Compute p roots – Roots are either real (positive or negative) – Complex conjugate pairs Purdue Aeroelasticity 31

Eigenvalue roots i wg=s is the estimated system damping i There are “m” computed values of w at the airspeed V i You chose a value of k=wb/V, was it correct? – “line up” the frequencies to make sure k, w and V are consistent Purdue Aeroelasticity 32

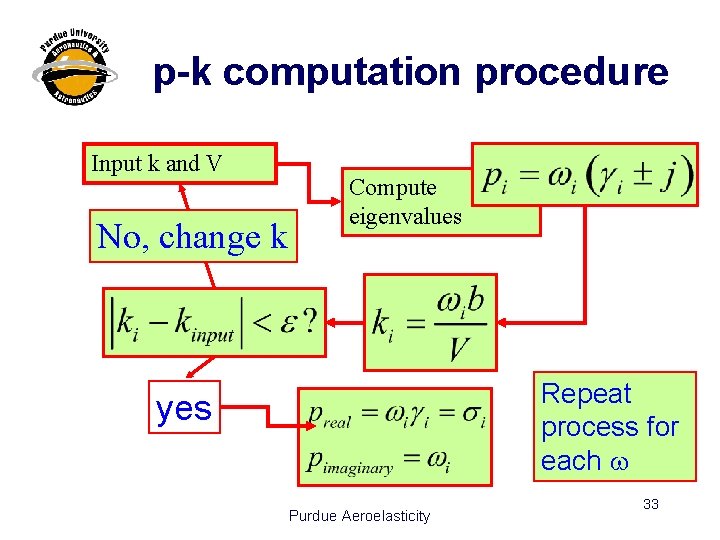
p-k computation procedure Input k and V No, change k Compute eigenvalues Repeat process for each w yes Purdue Aeroelasticity 33

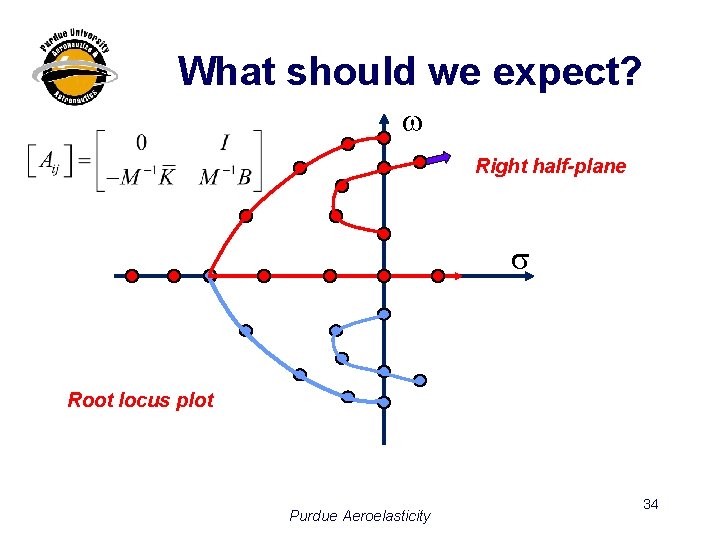
What should we expect? w Right half-plane s Root locus plot Purdue Aeroelasticity 34

Back-up slides for Problem 9. 2 Purdue Aeroelasticity 35

A comparison between V-g and p-k Purdue Aeroelasticity 36

A comparison between V-g and p-k Purdue Aeroelasticity 37

A comparison between V-g and p-k Purdue Aeroelasticity 38

A comparison between V-g and p-k Purdue Aeroelasticity 39

Flutter in action Accident occurred APR-27 -95 at STEVENSON, AL Aircraft: WITTMAN O&O, registration: N 41 SW Injuries: 2 Fatal. REPORTS FROM GROUND WITNESSES, NONE OF WHOM ACTUALLY SAW THE AIRPLANE, VARIED FROM HEARING A HIGH REVVING ENGINE TO AN EXPLOSION. EXAMINATION OF THE WRECKAGE REVEALED THAT THE AIRPLANE EXPERIENCED AN IN-FLIGHT BREAKUP. DAMAGE AND STRUCTURAL DEFORMATION WAS INDICATIVE OF AILERONWING FLUTTER. WING FABRIC DOPE WAS DISTRESSED OR MISSING ON THE AFT INBOARD PORTION OF THE LEFT WING UPPER SURFACE AND ALONG THE ENTIRE LENGTH OF THE TOP OF THE MAIN SPAR. LARGE AREAS OF DOPE WERE ALSO MISSING FROM THE LEFT WING UNDERSURFACE. THE ENTIRE FABRIC COVERING ON THE UPPER AND LOWER SURFACES OF THE RIGHT WING HAD DELAMINATED FROM THE WING PLYWOOD SKIN. THE DOPED FINISH WAS SEVERELY DISTRESSED AND MOTTLED. THE FABRIC COVERING HAD NOT BEEN INSTALLED IN ACCORDANCE WITH THE POLY-FIBER COVERING AND PAINT MANUAL; THE PLYWOOD WAS NOT TREATED WITH THE POLYBRUSH COMPOUND. Probable Cause AILERON-WING FLUTTER INDUCED BY SEPARATION AT THE TRAILING EDGE OF AN UNBONDED PORTION OF WING FABRIC AT AN AILERON WING STATION. THE DEBONDING OF THE WING FABRIC WAS A RESULT OF IMPROPER INSTALLATION. Purdue Aeroelasticity 40

Things you should know Royal Aircraft Establishment The RAE started as HM Balloon Factory. From 1911 -18 it was called the Royal Aircraft Factory, but was changed its name to Royal Aircraft Establishment to avoid confusion with the newly established Royal Air Force. Farnborough was known as a center of excellence for aircraft research. Major flutter research was conducted there. Famous R&M’s such as the “flutter bible” came from this facility. The RAE played a major role in both World Wars. So confident was Hitler that he could occupy England with relative ease that he spared the RAE from bombing in the hope of benefiting from its research. Recently the RAE (now known as the Royal Aerospace Establishment) was absorbed into the DRA (Defence Research Agency), itself renamed as DERA (Defence Evaluation and Research Agency). The world famous initials are no more. Purdue Aeroelasticity 41