A VLSI Architecture for the 2 D Discrete

A VLSI Architecture for the 2 -D Discrete Wavelet Transform Zhiyu Liu Xin Zhou May 2004

Motivation n q To apply the knowledge learned in ECE 734 to practical problems Popular Methods n Folding n Parallel n Pipeline n Systolic n … q n n Possible Application Image Processing (Discrete Wavelet Transform) Speech Processing Communication Systems …

Goal To propose a new VLSI architecture to implement 2 -D Discrete Wavelet Transform (DWT). n q q q Based on RPA (Recursive Pyramid Algorithm) Parallel Architecture Systolic Architecture to Deal with Borders

Wavelet Transform n Wavelets: functions that cut up data into different frequency components, and then study each component with a resolution matched to its scale 2 2

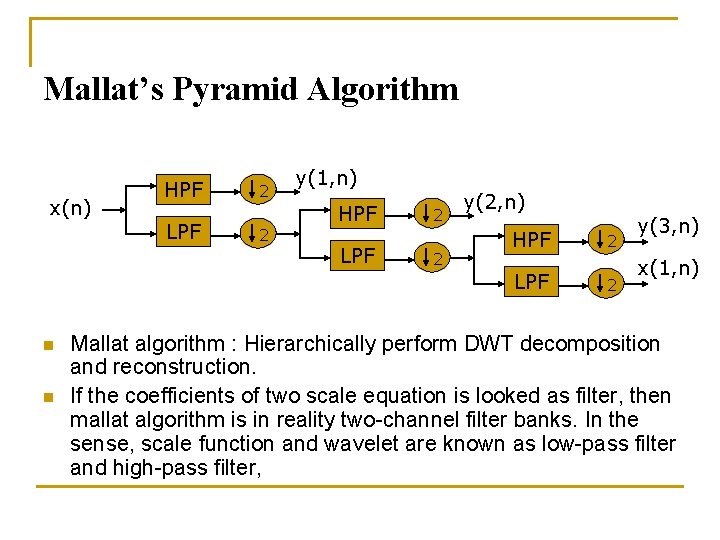
Mallat’s Pyramid Algorithm x(n) n n HPF LPF 2 2 y(1, n) HPF LPF 2 2 y(2, n) HPF LPF 2 2 y(3, n) x(1, n) Mallat algorithm : Hierarchically perform DWT decomposition and reconstruction. If the coefficients of two scale equation is looked as filter, then mallat algorithm is in reality two-channel filter banks. In the sense, scale function and wavelet are known as low-pass filter and high-pass filter,

Recursive Pyramid Algorithm n n RPA is a modification of Mallat’s PA In Mallat’s PA, each level is completely computed before the next RPA rearranges the order of the N outputs such that an output is scheduled at the `earliest' instance that it can be scheduled. The earliest instance is based on the following precedence relation: if the earliest `instance' of the ith octave clashes with that of the (i + 1)th octave, then the ith octave gets scheduled first.

Recursive Pyramid Algorithm(Cont. )

Recursive Pyramid Algorithm(Cont. 2)

Proposed Algorithm n Using Parallel Architecture to build up rowbased RPA and using the Systolic Architecture to deal with borders

Proposed Algorithm(Cont. ) n Row based RPA q q Intersperse the row operation of various octaves in between the first octave After each row operation, we proceed the column operation

Proposed Algorithm(Cont. 1) 0 Octave 1 Row + Octave 1 Column 1 Octave 2 Row + Octave 2 Column 2 Octave 1 Row + Octave 1 Column 3 Octave 3 Row + Octave 3 Column 4 Octave 1 Row + Octave 1 Column 5 Octave 2 Row + Octave 2 Column 6 Octave 1 Row + Octave 1 Column … …

Proposed Algorithm(Cont. 2) --- Hardware Implementation Architecture

Proposed Algorithm(Cont. 3) -- Dealing with Borders n Decomposition of Periodic Extension RPA n Reconstruction of Periodic Extension RPA

Proposed Algorithm(Cont. 4)

Conclusion n Parallel q n Periodic extension q q n To speed up the chip Implement the perfect reconstruction Compute coefficients. Future work q Theoretic analysis