A Venndiagram hasznlata 2 9 dia A Venn

A Venn-diagram használata 2 -9. dia: A Venn diagram használatáról 10 -15. dia: A Venn diagram használatára 3 példa 16. dia: Elérhetőség, további anyagok, konzultációs időpont.

Tegyük fel, hogy van egy dobozunk kisgolyókkal és kiskockákkal (nemkisgolyókkal), amik lehetnek piros vagy sárgászöld színűek (nempiros színűek), ehetőek vagy nem ehetőek. Ha van két nyers információnk a dobozban lévő dolgokról, hogyan juthatunk harmadik információhoz? Ilyesmiről szólnak a szillogizmusok. Hogyan lehet őket látványosan bizonyítani vagy pusztán átlátni? Ehhez kell a Venn-diagram.

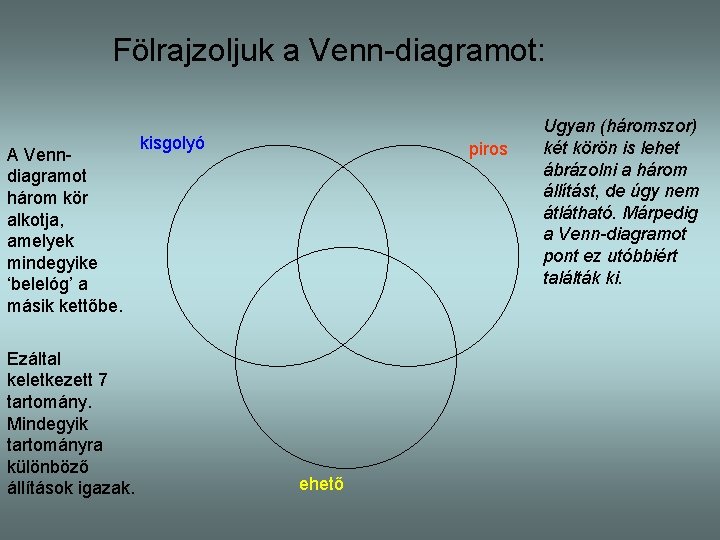
Fölrajzoljuk a Venn-diagramot: A Venndiagramot három kör alkotja, amelyek mindegyike ‘belelóg’ a másik kettőbe. Ezáltal keletkezett 7 tartomány. Mindegyik tartományra különböző állítások igazak. kisgolyó piros ehető Ugyan (háromszor) két körön is lehet ábrázolni a három állítást, de úgy nem átlátható. Márpedig a Venn-diagramot pont ez utóbbiért találták ki.

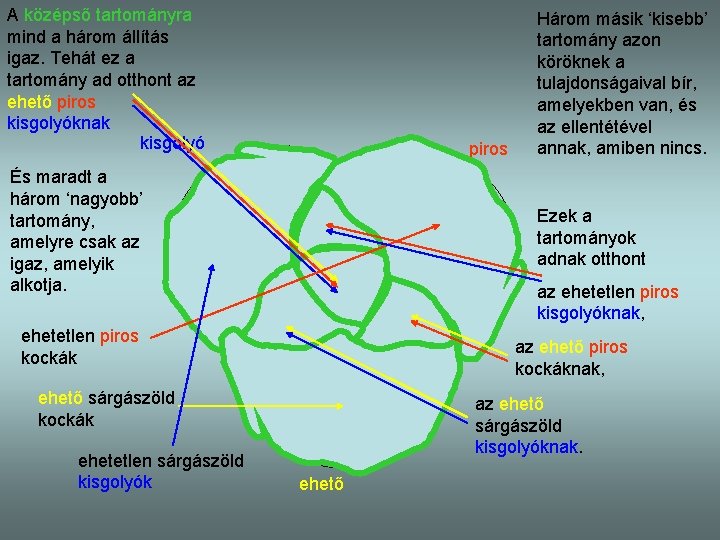
A középső tartományra mind a három állítás igaz. Tehát ez a tartomány ad otthont az ehető piros kisgolyóknak kisgolyó piros És maradt a három ‘nagyobb’ tartomány, amelyre csak az igaz, amelyik alkotja. Ezek a tartományok adnak otthont az ehetetlen piros kisgolyóknak, ehetetlen piros kockák az ehető piros kockáknak, ehető sárgászöld kockák ehetetlen sárgászöld kisgolyók Három másik ‘kisebb’ tartomány azon köröknek a tulajdonságaival bír, amelyekben van, és az ellentétével annak, amiben nincs. az ehető sárgászöld kisgolyóknak. ehető

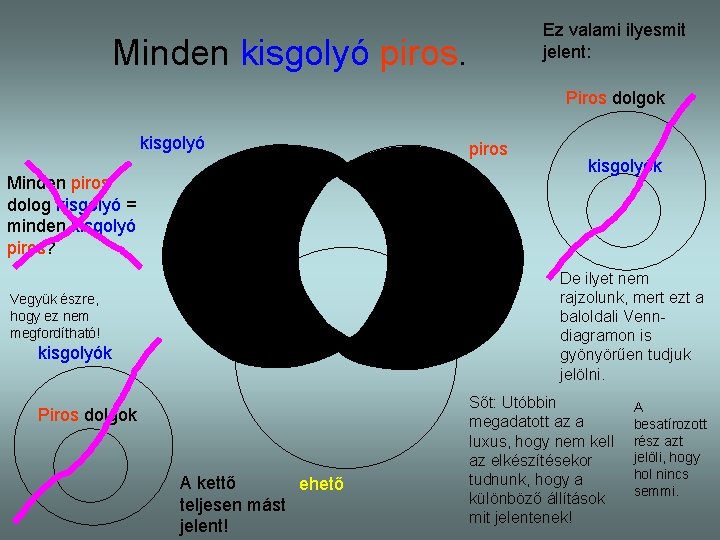
Ez valami ilyesmit jelent: Minden kisgolyó piros. Piros dolgok kisgolyó Minden piros dolog kisgolyó = minden kisgolyó piros? piros kisgolyók De ilyet nem rajzolunk, mert ezt a baloldali Venndiagramon is gyönyörűen tudjuk jelölni. Vegyük észre, hogy ez nem megfordítható! kisgolyók Piros dolgok A kettő ehető teljesen mást jelent! Sőt: Utóbbin megadatott az a luxus, hogy nem kell az elkészítésekor tudnunk, hogy a különböző állítások mit jelentenek! A besatírozott rész azt jelöli, hogy hol nincs semmi.

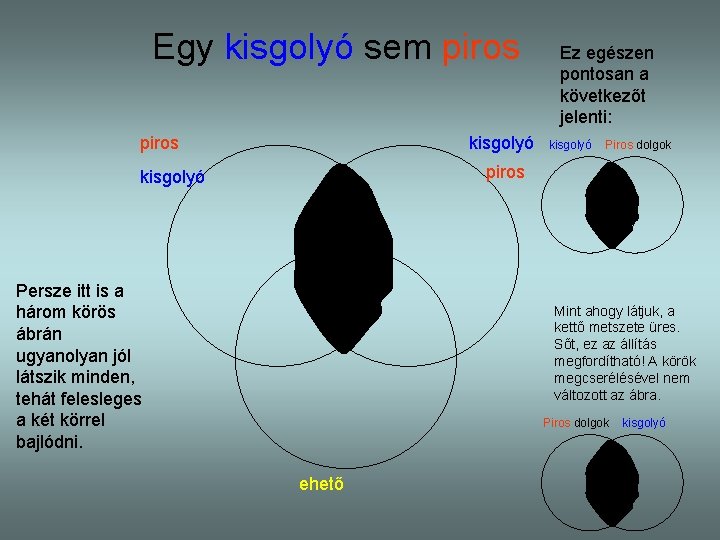
Egy kisgolyó sem piros kisgolyó Ez egészen pontosan a következőt jelenti: kisgolyó Piros dolgok piros kisgolyó Persze itt is a három körös ábrán ugyanolyan jól látszik minden, tehát felesleges a két körrel bajlódni. Mint ahogy látjuk, a kettő metszete üres. Sőt, ez az állítás megfordítható! A körök megcserélésével nem változott az ábra. Piros dolgok ehető kisgolyó

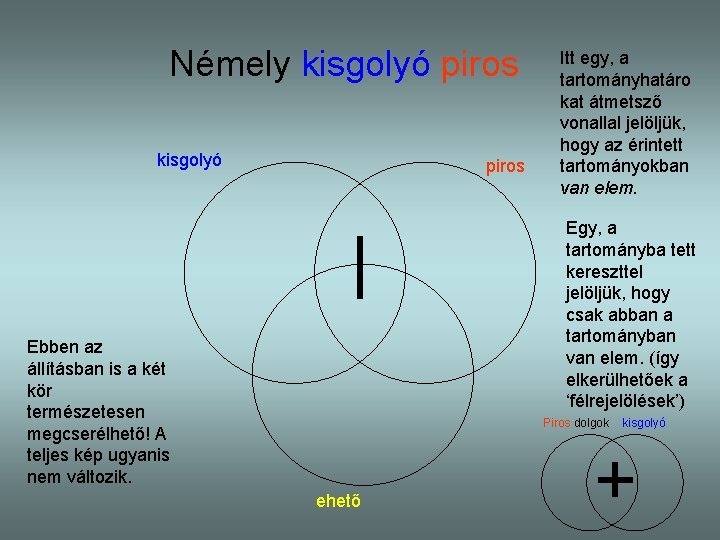
Némely kisgolyó piros Itt egy, a tartományhatáro kat átmetsző vonallal jelöljük, hogy az érintett tartományokban van elem. Egy, a tartományba tett kereszttel jelöljük, hogy csak abban a tartományban van elem. (így elkerülhetőek a ‘félrejelölések’) Ebben az állításban is a két kör természetesen megcserélhető! A teljes kép ugyanis nem változik. Piros dolgok ehető kisgolyó

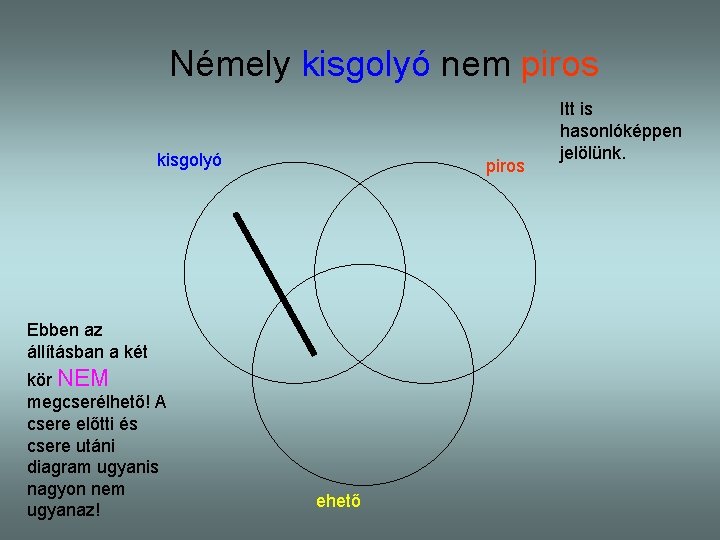
Némely kisgolyó nem piros kisgolyó piros Ebben az állításban a két kör NEM megcserélhető! A csere előtti és csere utáni diagram ugyanis nagyon nem ugyanaz! ehető Itt is hasonlóképpen jelölünk.

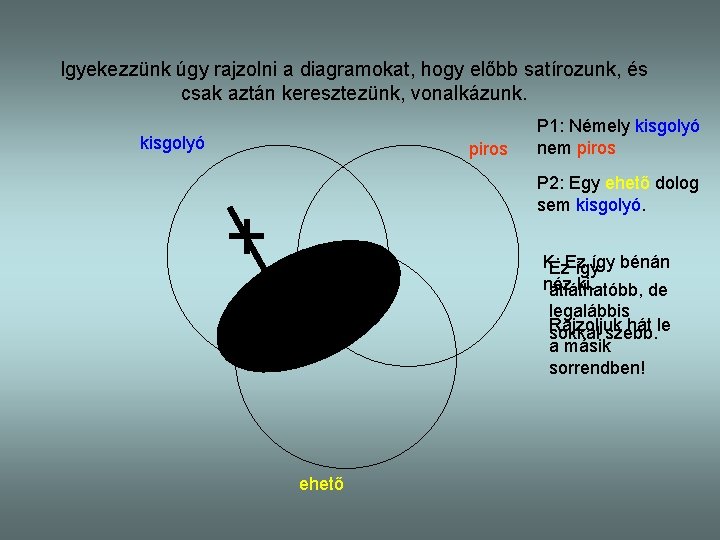
Igyekezzünk úgy rajzolni a diagramokat, hogy előbb satírozunk, és csak aztán keresztezünk, vonalkázunk. kisgolyó piros P 1: Némely kisgolyó nem piros P 2: Egy ehető dolog sem kisgolyó. K: Ez. Ez ígyígy bénán néz ki. átláthatóbb, de legalábbis Rajzoljuk hát le sokkal szebb. a másik sorrendben! ehető

Igaz-e hogy… • P 1: Minden kisgolyó piros. • P 2: Minden ami piros, az ehető. • K: Minden kisgolyó ehető. 1. lépés: ‘Lerajzoljuk’ a premisszákat 2. lépés: Fejben, vagy egy másik rajzon ‘lerajzoljuk’ a konklúziót. 3. Lépés: Eltöprengünk azon, vajon benne van-e a konklúzió rajza a premisszás rajzban? 4. Lépés: Akármilyen nehéz is, szöveggel megpróbálunk mindent megindokolni.

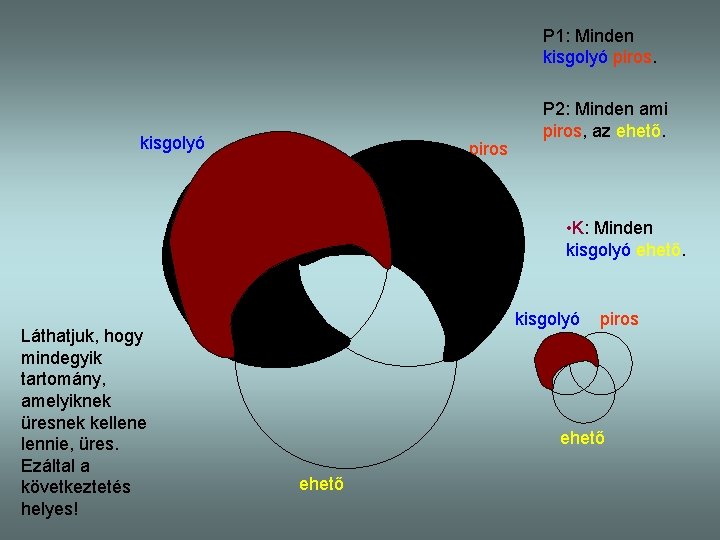
P 1: Minden kisgolyó piros P 2: Minden ami piros, az ehető. • K: Minden kisgolyó ehető. Láthatjuk, hogy mindegyik tartomány, amelyiknek üresnek kellene lennie, üres. Ezáltal a következtetés helyes! kisgolyó piros ehető

Igaz-e hogy… • P 1: Némely piros dolog kisgolyó. • P 2: Egy ehető dolog sem kisgolyó. • K: Némely piros dolog nem ehető.

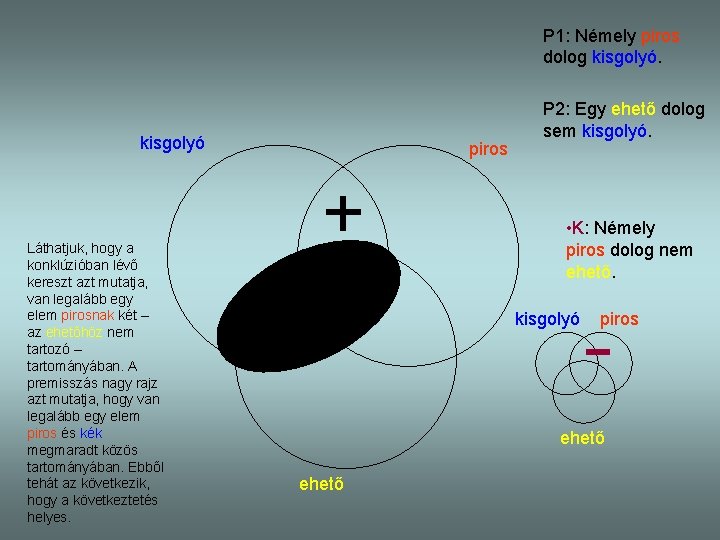
P 1: Némely piros dolog kisgolyó Láthatjuk, hogy a konklúzióban lévő kereszt azt mutatja, van legalább egy elem pirosnak két – az ehetőhöz nem tartozó – tartományában. A premisszás nagy rajz azt mutatja, hogy van legalább egy elem piros és kék megmaradt közös tartományában. Ebből tehát az következik, hogy a következtetés helyes. piros P 2: Egy ehető dolog sem kisgolyó. • K: Némely piros dolog nem ehető. kisgolyó piros ehető

Igaz-e hogy… • P 1: Némely piros dolog nem kisgolyó. • P 2: Minden ehető dolog kisgolyó. • K: Egy piros dolog sem ehető.

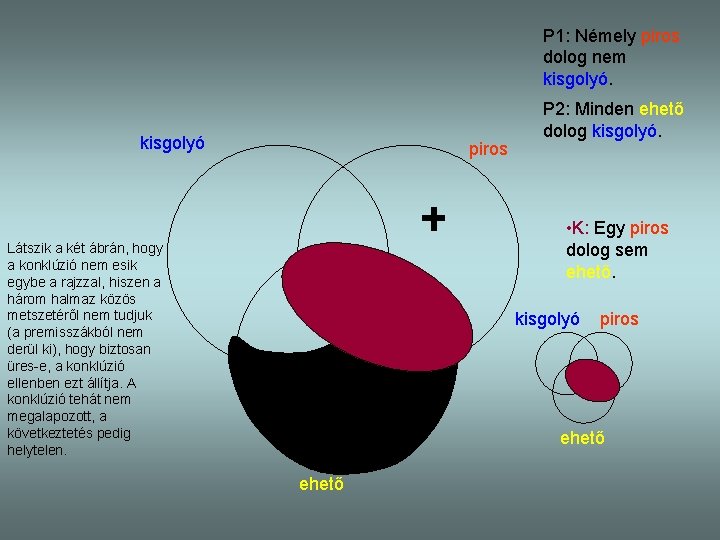
P 1: Némely piros dolog nem kisgolyó piros P 2: Minden ehető dolog kisgolyó. • K: Egy piros dolog sem ehető. Látszik a két ábrán, hogy a konklúzió nem esik egybe a rajzzal, hiszen a három halmaz közös metszetéről nem tudjuk (a premisszákból nem derül ki), hogy biztosan üres-e, a konklúzió ellenben ezt állítja. A konklúzió tehát nem megalapozott, a következtetés pedig helytelen. kisgolyó piros ehető

Még nagyon sok hasznos információ található a Forrai Gábor által készített internetes tananyagban is: http: //www. uni-miskolc. hu/~filtort/erveles/4 dederv. ppt Bárki, akinek problémája van, vagy hibát talál valahol, legyen az súlyos logikai vagy helyesírási hiba, írjon erre a címre: thuluviel@hu. inter. net Erre a címre ezen kívül is mindenféle tananyaggal kapcsolatos kérdést szívesen várok. A konzultációs időpontomban is várok minden kedves érdeklődőt. Konzultáció a Logika tanszéken, Csütörtökön 16. 00 -tól, Szerdán 10. 00 -től. Ha 15 percig nem jön senki, és nem szólt nekem előtte senki ez irányú szándékáról, akkor elmegyek. Molnár Attila