A Uniform Optimization Technique for Offset Assignment Problems

A Uniform Optimization Technique for Offset Assignment Problems Rainer Leupers, Fabian David University of Dortmund, Germany Dept. of Computer Science 12 1 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

Overview • Offset assignment problem • Related work • Genetic algorithm approach • Exploitation of modify registers • Results & conclusions 2 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

Offset assignment problem Context: Code generation for DSPs Given: DSP address generation unit (AGU) with # address registers (ARs): k # modify registers (MRs): m auto-increment range (AIR): r Auto-increment capabilities: AR[i] += d, d <= r AR[i] += MR[j] Other address computations cause extra code ! Problem: Assign program variables to memory addresses and ARs, such that the use of auto-increment address computations is maximized ! 3 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

Offset assignment: example variables: { a, b, c, d } access sequence: (b, d, a, c, b, a, d, a, c, d) Layout 1 0 1 2 3 cost: 9 4 a b c d AR = 1 AR += 2 AR -= 3 AR += 2 AR ++ AR -= 3 AR += 2 AR - AR += 3 AR -= 3 AR += 2 AR ++ Layout 2 0 1 2 3 c a d b cost: 5 AR = 3 AR - AR += 2 AR - AR += 3 AR -= 2 AR ++ AR - AR += 2 Rainer Leupers, University of Dortmund, Computer Science Dept. Simple Offset Assignment: k= 1 m=0 r= 1 ISSS ´ 98

Related work Offset assignment for different AGU models: #ARs #MRs AIR [Bartley 92] 1 - 1 [Liao 95] k - 1 [Leupers 96] k m 1 [Wess 97] 1 - 2 [Sudarsanam 97] k - r this work k m r Further work on address optimization for fixed layout 5 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

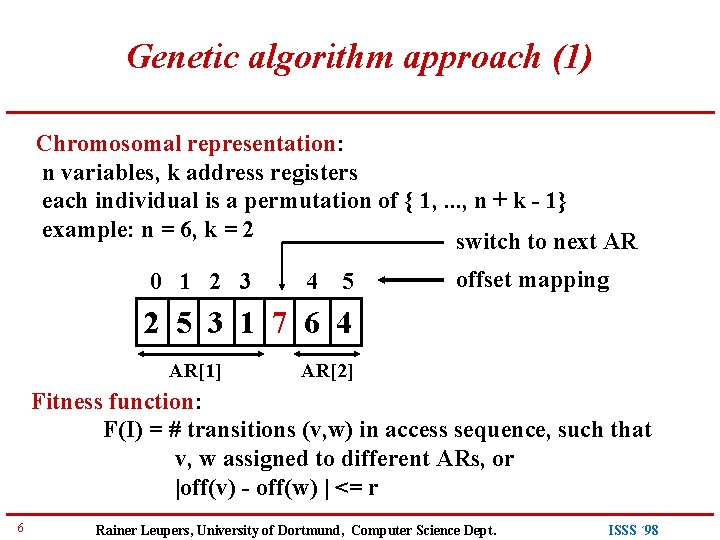
Genetic algorithm approach (1) Chromosomal representation: n variables, k address registers each individual is a permutation of { 1, . . . , n + k - 1} example: n = 6, k = 2 switch to next AR 0 1 2 3 4 5 offset mapping 2 5 3 1 7 6 4 AR[1] AR[2] Fitness function: F(I) = # transitions (v, w) in access sequence, such that v, w assigned to different ARs, or |off(v) - off(w) | <= r 6 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

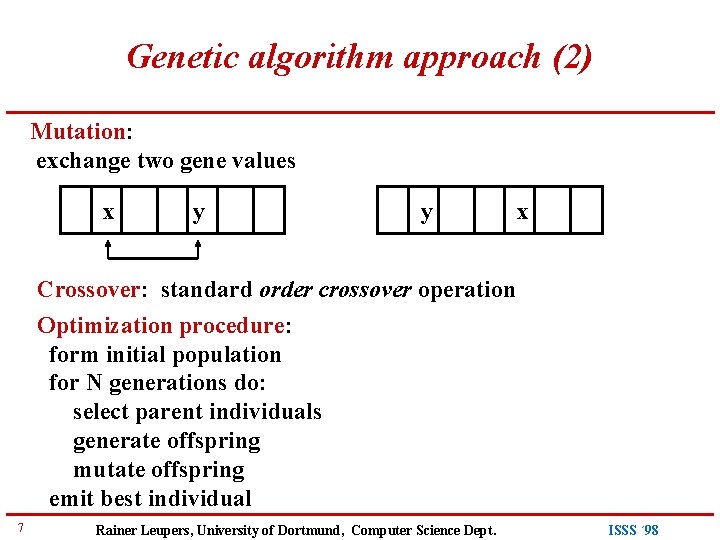
Genetic algorithm approach (2) Mutation: exchange two gene values x y y x Crossover: standard order crossover operation Optimization procedure: form initial population for N generations do: select parent individuals generate offspring mutate offspring emit best individual 7 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

Exploitation of modify registers (1) [Leupers 96]: Modification of Belady‘s optimal page replacement algorithm can be used for optimal exploitation of m MRs for a fixed offset assignment (only postpass optimization) PRA(I) = # address computations that can be saved by exploiting MRs for a given offset assignment modified fitness function: F´(I) = F(I) + PRA(I) => exploitation of MRs included into GA ! 8 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98

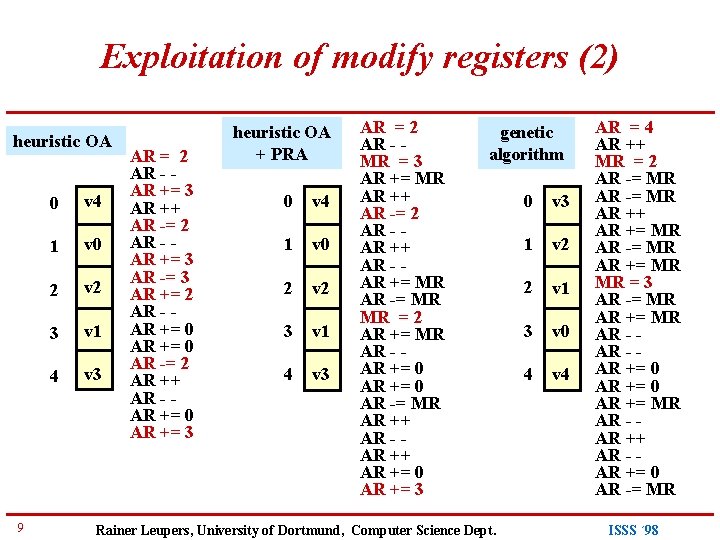
Exploitation of modify registers (2) heuristic OA 9 0 v 4 1 v 0 2 v 2 3 v 1 4 v 3 AR = 2 AR - AR += 3 AR ++ AR -= 2 AR - AR += 3 AR -= 3 AR += 2 AR - AR += 0 AR -= 2 AR ++ AR - AR += 0 AR += 3 heuristic OA + PRA 0 v 4 1 v 0 2 v 2 3 v 1 4 v 3 AR = 2 AR - MR = 3 AR += MR AR ++ AR -= 2 AR - AR ++ AR - AR += MR AR -= MR MR = 2 AR += MR AR - AR += 0 AR -= MR AR ++ AR - AR ++ AR += 0 AR += 3 genetic algorithm Rainer Leupers, University of Dortmund, Computer Science Dept. 0 v 3 1 v 2 2 v 1 3 v 0 4 v 4 AR = 4 AR ++ MR = 2 AR -= MR AR ++ AR += MR AR -= MR AR += MR MR = 3 AR -= MR AR += MR AR - AR += 0 AR += MR AR - AR ++ AR - AR += 0 AR -= MR ISSS ´ 98

Results & conclusions Statistical evaluation: ! 32 % improvement over OA heuristic with postpass MR optimization ! 32 % improvement over Wess‘ simulated annealing technique ! Runtime: typically 10 CPU seconds (Pentium II) Main contributions: ! First uniform offset assignment technique, arbitrary k, m, r values ! Significant improvements in code quality over previous techniques, largely due to better exploitation of MRs 10 Rainer Leupers, University of Dortmund, Computer Science Dept. ISSS ´ 98