A Truthful 2 approximation Mechanism for the Steiner

A Truthful 2 -approximation Mechanism for the Steiner Tree Problem

The Steiner Tree problem n INPUT: n n n Undirected, weighted graph G=(V, E, c) N V: set of terminal nodes OUTPUT: n a tree T spanning N of minimum total cost, i. e. , which minimizes c(T)= e Tc(e)

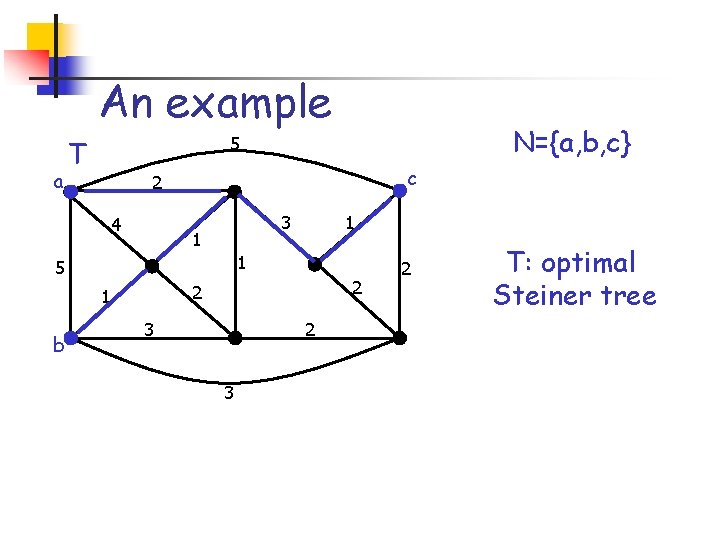
An example a T c 2 4 3 1 1 1 5 2 2 1 b N={a, b, c} 5 3 2 T: optimal Steiner tree

About Steiner Tree problem n n It is NP-hard It is approximable within 1. 55 n Robins, Zelikovsky (2000)

Steiner Tree game n n n Each edge e is controlled by a selfish agent Ae Only Ae knows te (weight of the edge e) We want to compute a “good” solution w. r. t. the true costs We do it by designing a mechanism Our mechanism: n n n Asks each agent to report her cost Computes a solution using an output algorithm g(٠) Hands payments pe to each agent Ae using some payment function p

More formally n Feasible solutions: n n Type of agent Ae: n n n e: weight of edge e Intuition: e is the cost Ae incurs whenever she uses e Ae’s valuation of T F: n n F: set of all trees in G spanning N ve( e, T)= e if e E(T), 0 otherwise SCF: minimum Steiner tree of G=(V, E, ) with terminals N

How to design a truthful mechanism for the problem? Notice that: the (true) total weight of a feasible T is: e E ve( e, T) the problem is utilitarian! …VCG mechanisms apply

VCG mechanism n M= <g(r), p(x)>: g(r): arg minx F j vj(rj, x) n pe(x): for each e E: n pe = j≠e vj(rj, g(r-e)) - j≠e vj(rj, x) g(r) should compute an optimal solution!!! What to do? …we look for (approximated) one-parameter mechanisms! L. Gualà, G. Proietti, A Truthful (2 -2/k)-Approximation Mechanism for the Steiner Tree Problem with k Terminals, COCOON’ 05

Our goal: to design a mechanism satisfying: n 1. 2. 3. g(٠) is monotone Solution returned by g(٠) is a “good” solution, i. e. an approximated solution g(٠) and p(٠) computable in polynomial time

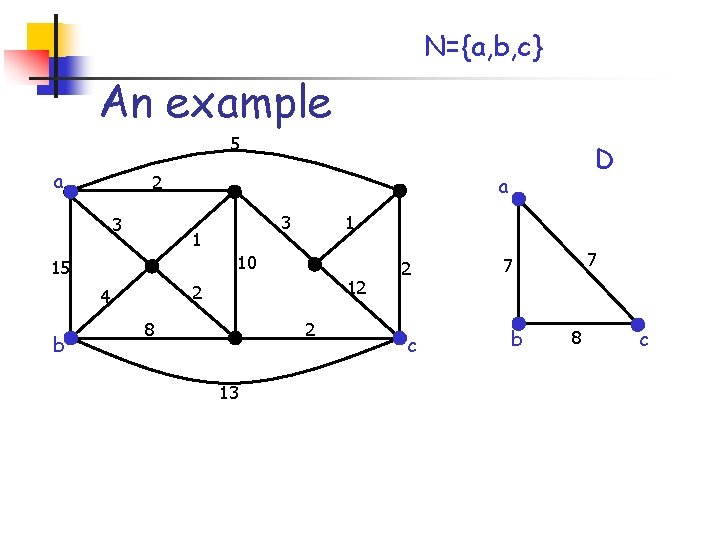
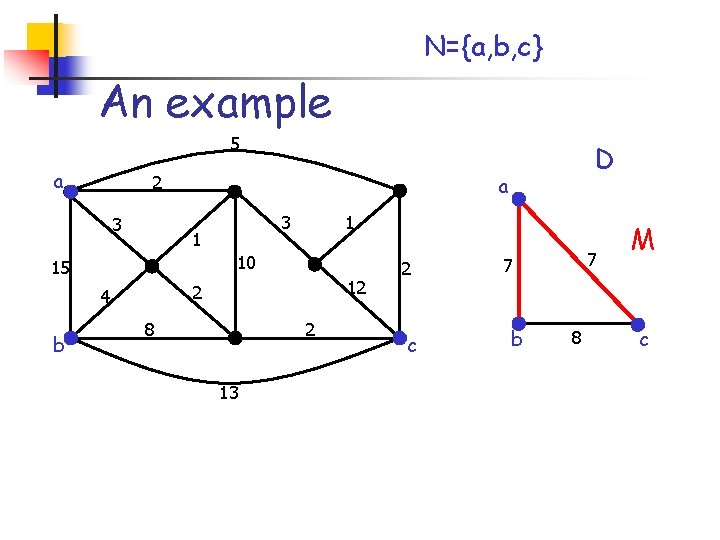
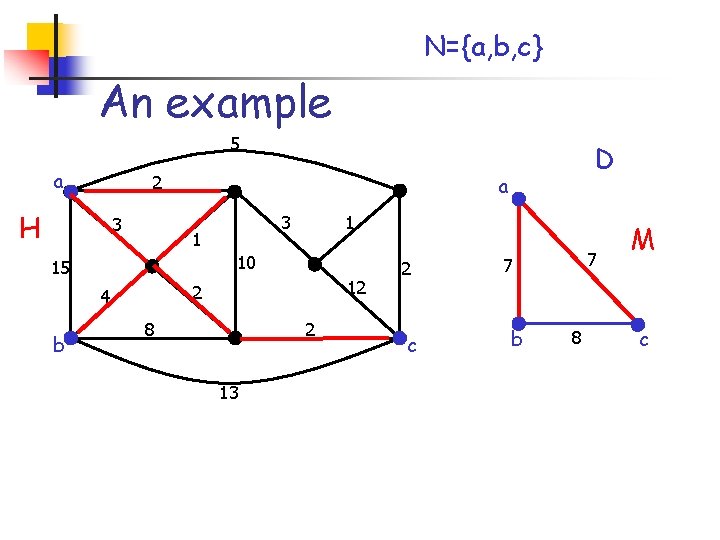
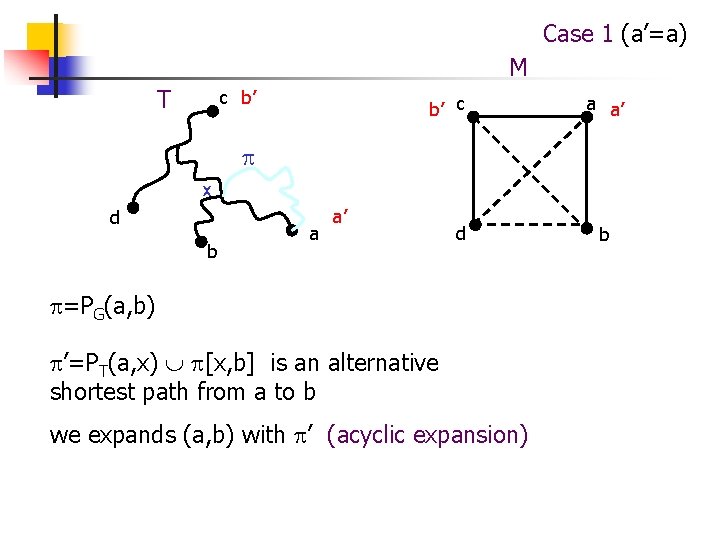
A 2 -approximation algorithm 1. Build the weighted complete graph D with node set N 1. 2. 3. 4. For every pair of nodes in N, w(a, b): = d. G(a, b) Compute an MST M of D Expand any edge of M with the corresponding shortest path. This defines a subgraph H of G Return any feasible tree T which is a subgraph of H

N={a, b, c} An example 5 a 2 3 a 1 10 15 b 3 1 12 2 4 D 8 2 13 2 c 7 7 b 8 c

N={a, b, c} An example 5 a 2 3 a 1 10 15 b 3 1 12 2 4 D 8 2 13 2 c 7 7 b 8 M c

N={a, b, c} An example 5 a 2 H 3 a 1 10 15 b 3 1 12 2 4 D 8 2 13 2 c 7 7 b 8 M c

N={a, b, c} An example 5 a 2 T 3 a 1 10 15 b 3 1 12 2 4 D 8 2 13 2 c 7 7 b 8 M c

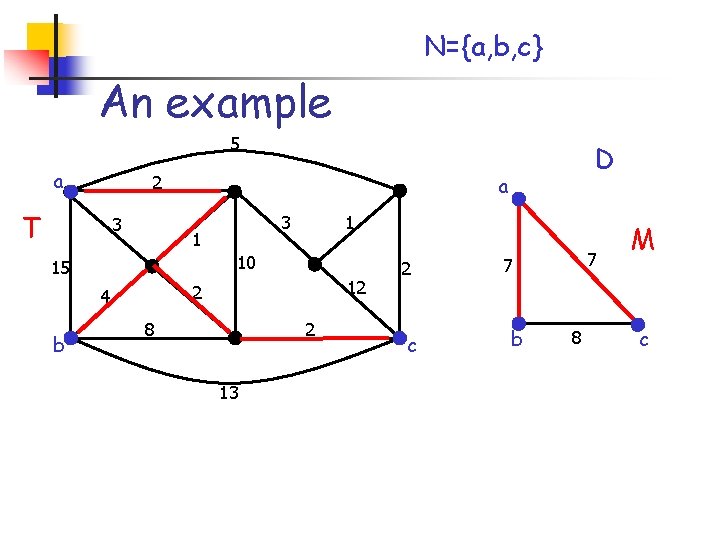
Theorem [Takahashi, Matsuyama, ’ 80] The algorithm is a 2 -approximation algorithm for the Steiner tree problem, i. e. it returns a solution with cost at most twice the cost of the optimal solution. Is the algorithm monotone? . . good question! It depends on Steps 3 and 4

Definition of g(٠) We modify the 2 -apx algorithm in order to garantee n 1. 2. Monotonicity Efficiency w. r. t. the computation to the threshold values Idea: we can guarantee an acyclic expansion of M

High level description of g(٠) 1. Compute D; M=MST(D) 2. Let r be any terminal node. T=({r}, ). N(T)={r} 3. At each step g(٠) reaches a new terminal node b (until N(T)=N) 1. Choose an edge (a, b) of M s. t. a N(T) and b N(T) 2. Try to expand (a, b) whithout forming cycles 3. If this is not possible, look for an edge (a’, b) of D s. t. 1. (a’, b) admits an acyclic expansion 2. a’ N(T) 3. w(a’, b)=w(a, b) 4. M=M{(a, b)} {(a’, b)} 5. Expand (a’, b); N(T) = N(T) {b} 4. Return T and M

Expanding (a, b) n An edge (a, b) admits an acyclic expansion w. r. t. a current tree T if there is a shortest path =PG(a, b) s. t. n n [a, x] is already in the current tree [x, b] passes through no node of T (except x) Notation n Let e’=(a’, b’) E(M) n Removing e’ splits M into two subtrees n N(a’): the node set of the subtree containig a’ n N(b’): remaining nodes n CM(a’, b’): non-tree edges crossing the cut (N(a’), N(b’))

Expanding (a, b) Let =PG(a, b); Let x be the first node of T encountered along (traversing from b to a) Let (a’, b’) be any edge of the current M s. t. : 1. 2. 3. n n n 4. 5. a’, b’ N(T) ’=PT(a’, b’) passes through x a N(a’) N(T)=N(T) {b}; T=T [x, b]; if (a a’) then M=M{(a, b)} {(a’, b)}

Correctness (sketch) n n T is acyclic At any time M is an MST of D we have to show that the expanding step is correct There are 2 cases: n n a=a’ a a’

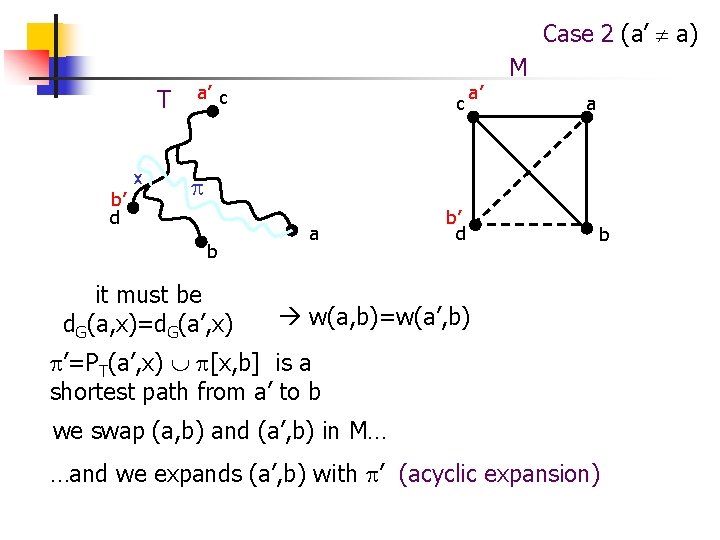
Case 1 (a’=a) M T c b’ b’ c a a’ x d b a a’ d =PG(a, b) ’=PT(a, x) [x, b] is an alternative shortest path from a to b we expands (a, b) with ’ (acyclic expansion) b

Case 2 (a’ a) T x b’ d a’ c c a’ M a b it must be d. G(a, x)=d. G(a’, x) a b’ d b w(a, b)=w(a’, b) ’=PT(a’, x) [x, b] is a shortest path from a’ to b we swap (a, b) and (a’, b) in M… …and we expands (a’, b) with ’ (acyclic expansion)

Lemma The algorithm g( ) is monotone proof It suffices to prove that any non-selected edge e it still non-selected when Ae raises her bid Notice: e does not belong to any shortest path selected in M Thus, if Ae raises her bid, the only edges in D which increase their weight are edges in E(D)E(M) …M remains an MST of D… …the solution computed by g() is the same and e is not selected

Computing the payments …we have to pay each selected edge e as its threshold value How much can Ae raise her bid before exiting from the computed solution?

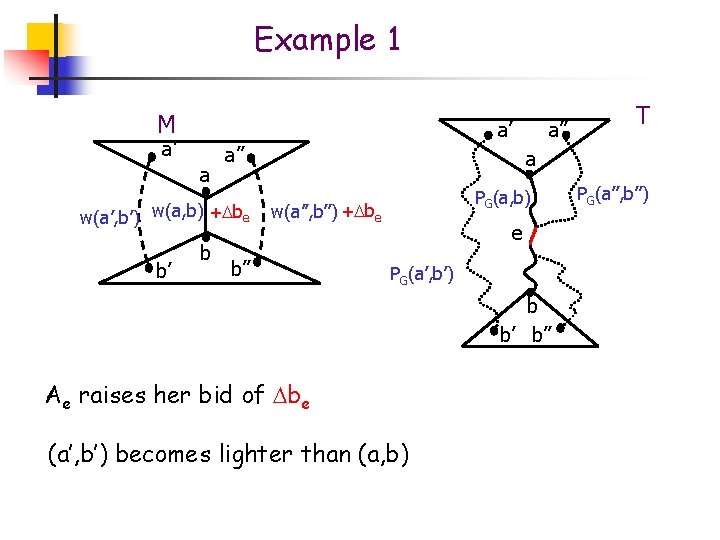
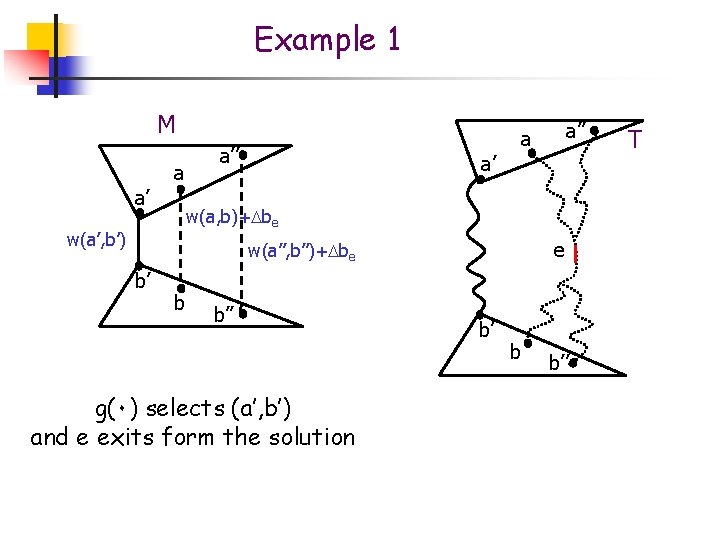
Example 1 M a’ a’ a a’’ w(a’, b’) w(a, b) + be b’ b a’’ T a PG(a, b) w(a’’, b’’) + be b’’ e PG(a’, b’) b b’ b’’ Ae raises her bid of be (a’, b’) becomes lighter than (a, b) PG(a’’, b’’)

Example 1 M a a’ a’ w(a, b)+ be w(a’, b’) e w(a’’, b’’)+ be b’ a’’ a b b’’ g(٠) selects (a’, b’) and e exits form the solution b’ b b’’ T

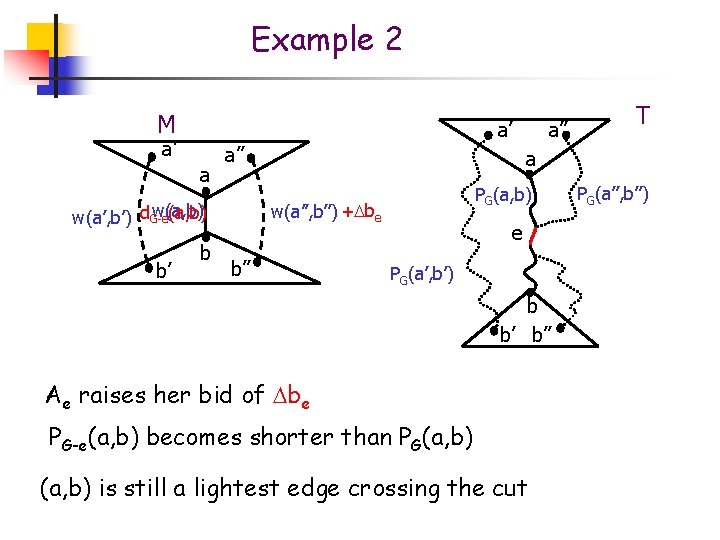
Example 2 M a’ a’ a a’’ b’ b T a PG(a, b) w(a’’, b’’) + be w(a, b) w(a’, b’) d. G-e a’’ b’’ e PG(a’, b’) b b’ b’’ Ae raises her bid of be PG-e(a, b) becomes shorter than PG(a, b) is still a lightest edge crossing the cut PG(a’’, b’’)

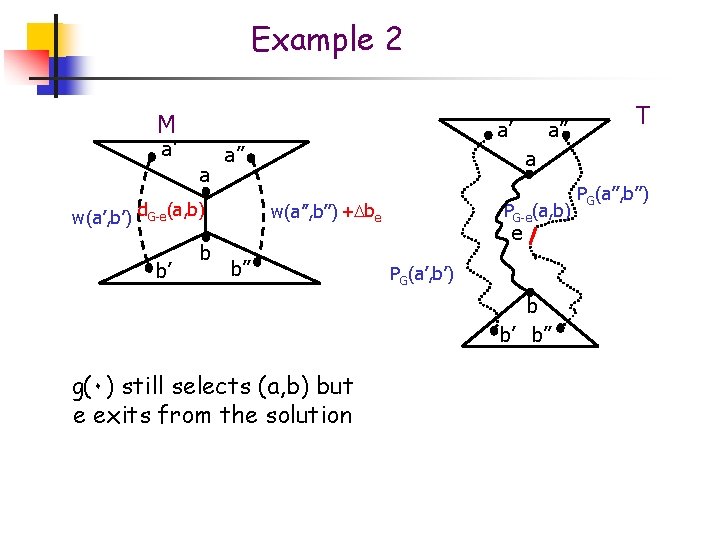
Example 2 M a’ a’ a a’’ w(a’, b’) d. G-e(a, b) b’ b a’’ T a w(a’’, b’’) + be b’’ PG-e(a, b) e PG(a’, b’) b b’ b’’ g(٠) still selects (a, b) but e exits from the solution PG(a’’, b’’)

…more formally… The image of e on M Im(e)={(a, b) E(M) | e PT(a, b)} (a, b) The threshold e is defined as for e w. r. t. the edge (a, b) Im(e) (a, b) e =be + min {(d. G-e(a, b) – d. G(a, b)), (swap(a, b)(e) – d. G(a, b))} where swap(a, b)(e)= min {d. G-e(a’, b’)} (a’, b’) CM(a, b)

Threshold of e If Im(e)={(a 1, b 1), … , (ah, bh)} (ai, bi) e = max { e i=1, . . , h } Easy to see: e can be computed in polynomial time

Theorem The running time of the mechanism is O((n+k 2)m log (m, n). The space used is O(n 2).