A Transformada de Fourier Discreta w A DTFT

A Transformada de Fourier Discreta w A DTFT transforma um sinal discreto num sinal continuo. No entanto o sinal continuo não pode ser processado numa maquina digital, PC, DSP… w Solução: DFT w Corresponde a amostragem da DTFT, ou seja a calcular a DTFT num conjunto finito de pontos: n H[k]=H(ej ) para = 2 k/N A amostragem no domínio da frequência é equivalente á formação de réplicas no domínio do tempo, o que conduz á série de fourier discreta. 1

A Transformada de Fourier Discreta w Existe uma correspondência entre sequências finitas e sequências periódicas n A Transformada de Fourier Discreta de uma sequência finita, corresponde à Transformada de Fourier da Sequência periódica obtida por repetição da sequência finita Série de Fourier (DFS) Transformada de Fourier Discreta (DFT) Transformada de Fourier (DTFT) 2

A Série de Fourier Discreta (DFS) Com: 3

A Série de Fourier Discreta (DFS) Série de Fourier Discreta Inversa Série de Fourier Discreta DFS – Discrete Fourier Series 4

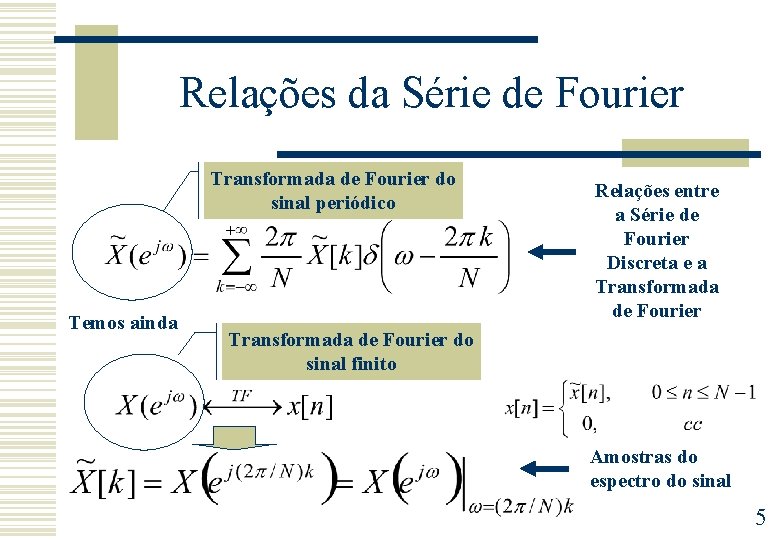
Relações da Série de Fourier Transformada de Fourier do sinal periódico Temos ainda Relações entre a Série de Fourier Discreta e a Transformada de Fourier do sinal finito Amostras do espectro do sinal 5

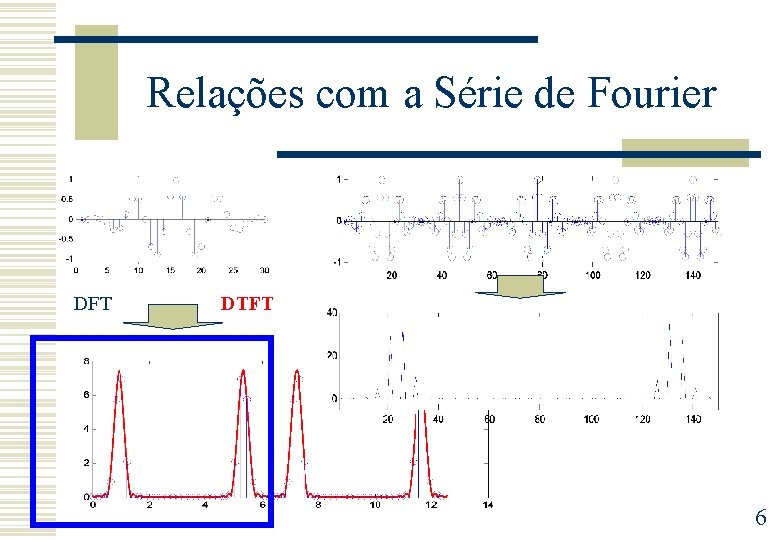
Relações com a Série de Fourier DFT DTFT 6

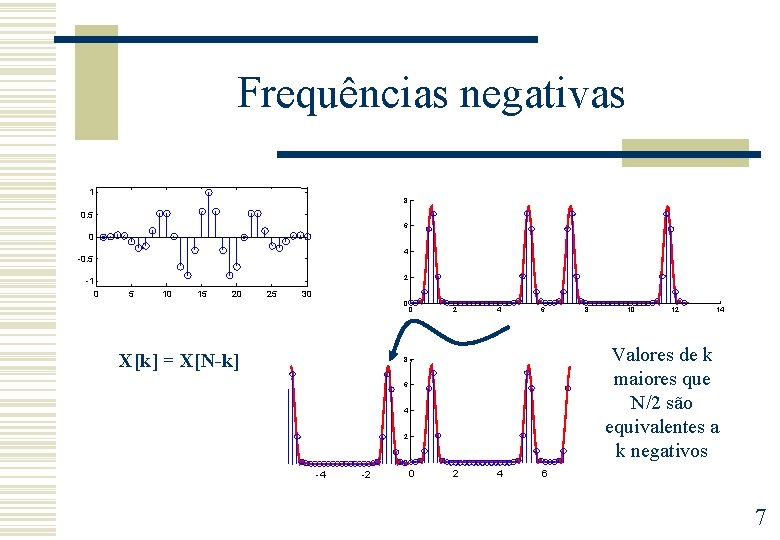
Frequências negativas 1 8 0. 5 6 0 4 -0. 5 2 -1 0 5 10 15 20 25 30 0 X[k] = X[N-k] 0 2 4 6 6 4 2 0 -2 10 12 14 Valores de k maiores que N/2 são equivalentes a k negativos 8 -4 8 0 2 4 6 7

Propriedades da Série de Fourier Discreta 8

Propriedades da Série de Fourier Discreta 9

A Transformada de Fourier Discreta (DFT) vector Matriz (dois índices) A matriz é Otonormal á parte do factor 1/N, sendo a inversa dada pelo matriz transposta, W-kn. N DFT- Discrete Fourier Transform 10

A Transformada de Fourier Discreta (DFT) A DFT corresponde a representação de x[n] numa base diferente, sendo sempre possível recuperar o sinal original. 11

Convolução Periódica (circular) w Convolução periódica A convolução no tempo só corresponde a multiplicação na frequência para a DFS. Para a DFT temos de utilizar a convolução circular. w Convolução circular A convolução circular é comutativa. 12

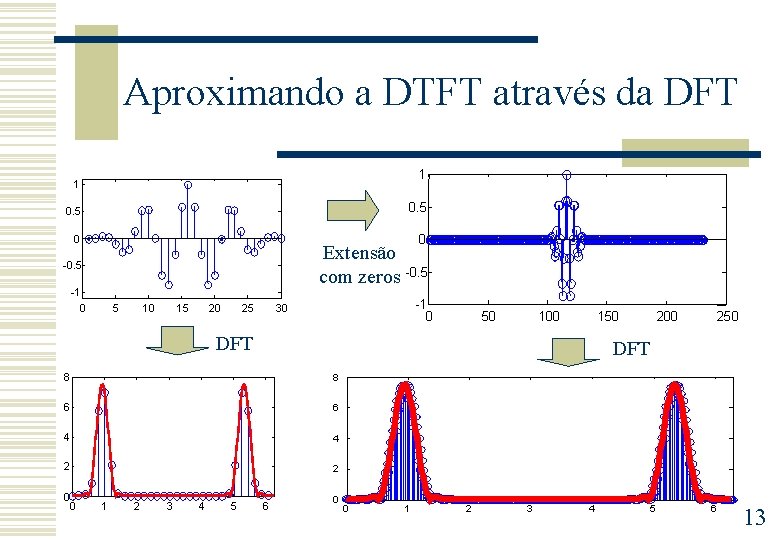
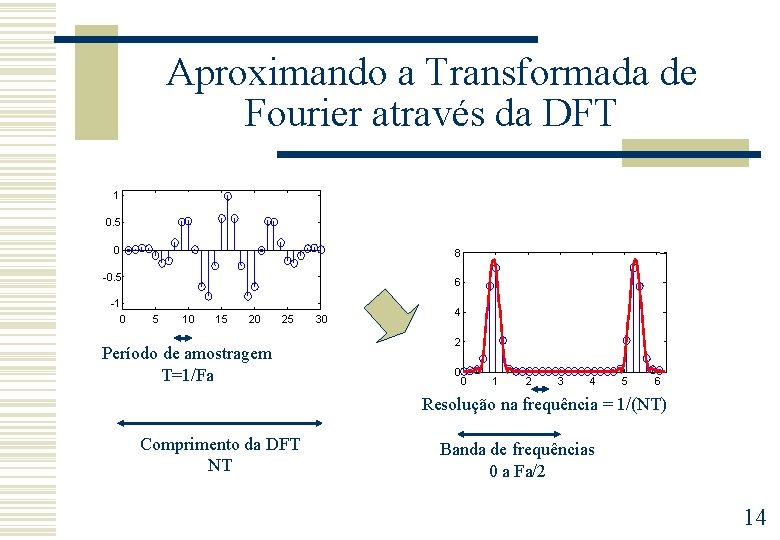
Aproximando a DTFT através da DFT 1 1 0. 5 0 0 Extensão com zeros -0. 5 -1 0 5 10 15 20 25 -1 0 30 50 100 150 DFT 8 6 6 4 4 2 2 0 1 2 3 4 5 250 DFT 8 0 200 6 0 0 1 2 3 4 5 6 13

Aproximando a Transformada de Fourier através da DFT 1 0. 5 0 8 -0. 5 6 -1 0 5 10 15 20 25 Período de amostragem T=1/Fa 30 4 2 0 0 1 2 3 4 5 6 Resolução na frequência = 1/(NT) Comprimento da DFT NT Banda de frequências 0 a Fa/2 14

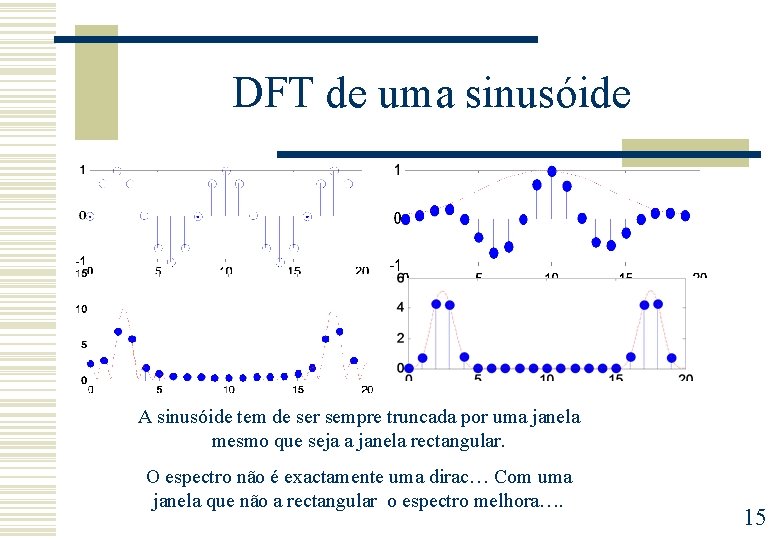
DFT de uma sinusóide A sinusóide tem de ser sempre truncada por uma janela mesmo que seja a janela rectangular. O espectro não é exactamente uma dirac… Com uma janela que não a rectangular o espectro melhora…. 15

Convolução Periódica (circular) DCT = DTFT Amostrada aliasing no tempo 16

Convolução Periódica (aliasing no tempo) z[n] z[n+N] z[n-N] resultado O produto do domínio da DFT é equivalente á convolução no domínio do tempo com aliasing N=10 17

Convolução Periódica Um atraso corresponde a rodar a sequência! 18

Goertzel Algorithm Notar que: x[n]=0 para n<0 19

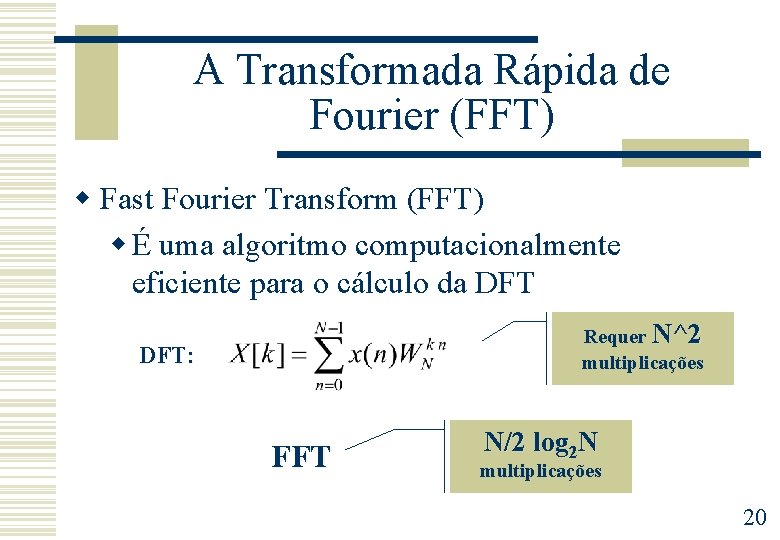
A Transformada Rápida de Fourier (FFT) w Fast Fourier Transform (FFT) w É uma algoritmo computacionalmente eficiente para o cálculo da DFT Requer N^2 multiplicações DFT: FFT N/2 log 2 N multiplicações 20

Principio Básico da FFT n A DFT de um vector de dimensão N pode ser calculada à custa de duas DFT de dimensão N/2 21

Grapho de uma FFT Butterfly FFT DFT x[n] X[k] 22

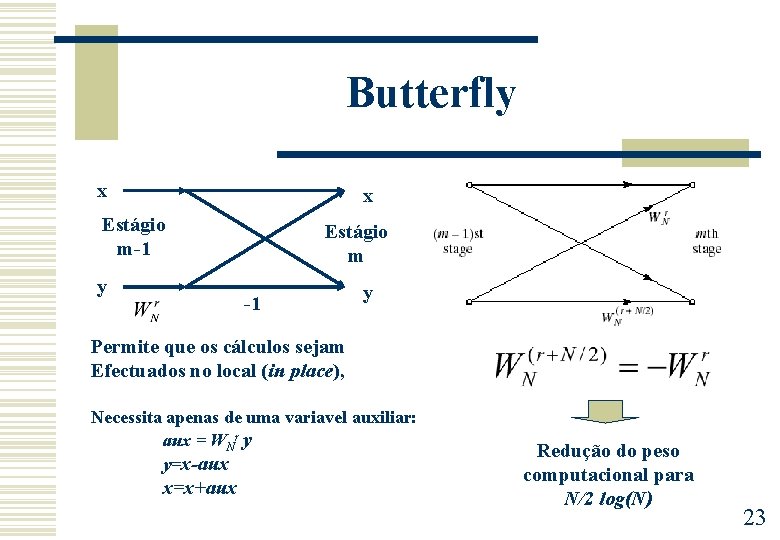
Butterfly x x Estágio m-1 y Estágio m -1 y Permite que os cálculos sejam Efectuados no local (in place), Necessita apenas de uma variavel auxiliar: aux = WNr y y=x-aux x=x+aux Redução do peso computacional para N/2 log(N) 23

Efeito do Ruído de Quantificação (virgula fixa) w Cada valor é calculado através de N-1 Butterflys w Em cada Butterfly há um arredondamento (o erro é b) Ruído no resultado (pior caso): (N-1) b Ruído no resultado assumindo sinais de ruído independentes: 1 Multiplicação Complexa = 4 Multiplicações reais 24

Efeito do Ruído de Quantificação w Para prevenir a saturação no pior caso do resultado devemos ter a componente real e complexa de x[n] menor que 1/N ou seja: N – Dimensão da FFT B – Numero de bits de para representação dos números Ou seja duplicar N implica perder um bit de relação sinal ruído Adicionando um escalamento de ½ às butterflys da FFT reduz a relação ruído sinal (N/S) para: Para processadores de virgula flutuante: Sinais de banda larga: 4 N 2 -2 B Sinais sinusoidais: 4 log 2 N 2 -2 B 25

Ordenação de bits Invertidos w 1ª divisão n n Xx 0 (pares) Xx 1 (impares) w 2ª divisão n n X 00 X 10 X 01 X 11 w 3ª divisão n n n n 000 100 010 110 001 101 011 111 Corresponde à ordenação tradicional mas com bits invertidos!! A reordenação pode ser efectuada “in place” 26

Twiddle factors w Necessários para o cálculo das butterflys w Calculo n n Off-line e armazenados numa tabela Iterativo: (pode ser efectuado com maior precisão) WNr+1 = WN WNr n Imediato: 27

Outras Implementações w Decimação na frequência n n Os coeficientes estão ordenados no tempo, e em ordem de bits invertidos na frequência! Não necessita de Bit_reversed_addressing para implementar a convolução com a FFT. w Outras bases que não a dois! n n Permite FFT de dimensão que não são potência de dois (sem extensão com zeros) Pode conduzir a um menor ruído de quantificação w Implementações com ordem directa na entrada e na saída n Não permite computação no local 28

Implementação w Blocos: corresponde ao cálculo de uma DFT de dimensão inferior Um loop externo para os diferentes estágios w Tamanho do bloco começa por ser dois e duplica para cada novo estádio. w Loop interno para diferentes blocos n n Cálculo de half_block_size Butterflys Os coeficientes das butterflys estão espaçados de half_block_size 29

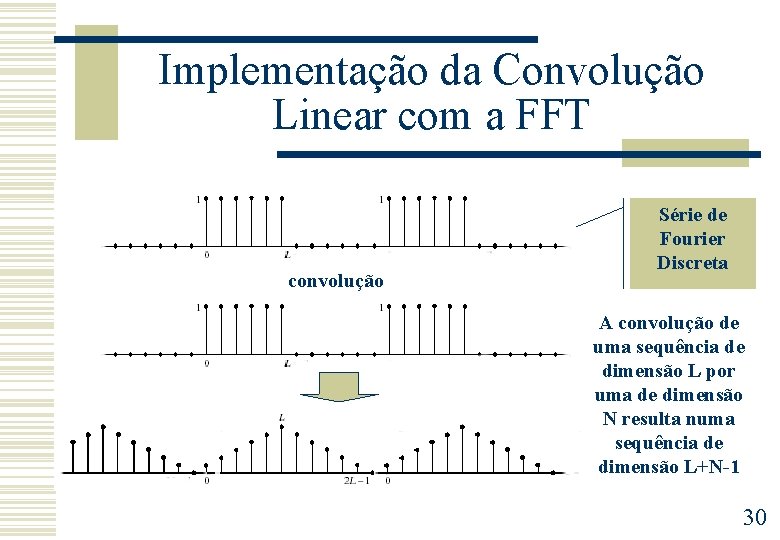
Implementação da Convolução Linear com a FFT convolução Série de Fourier Discreta A convolução de uma sequência de dimensão L por uma de dimensão N resulta numa sequência de dimensão L+N-1 30

Implementação da Convolução Linear com a FFT w Pretendemos obter a convolução de x[n] com y[n], 0 n < N w Estende-se x[n] e y[n] com N zeros w xe[n] = [x[n], 0. . . 0], ye[n] = [y[n], 0. . . 0] w Efectua-se a convolução circular de xe[n] com ye [n] #N #(N+M-1) #M Aplicações: Overlap and Add e Overlap and Save 31

Overlap and SAVE / Overlap and ADD w Implementação de filtros FIR, por blocos usando a FFT. w Implementação de convolução de dois vectores de sinais (x[n] e h[n]) com um dos vectores (x[n]) muito maior que outro (h[n]). w Solução: dividir x[n] em blocos: w Overlap and SAVE n Implementar a convolução circular de dois blocos do sinal de dados com a resposta ao impulso…. w Overlap and ADD n Implementar a convolução de um bloco do sinal de dados com a resposta ao impulso. Somar resultados de outros blocos. Desvantagem: atraso na saída 32

Overlap and Add x 0[n] convolução x 1[n] x 2[n] x 3[n] x 4[n] Convolução linear implementada com a FFT h[n] x 0[n]*h[n] x 1[n]*h[n] x 2[n]*h[n] Add y 0[n] y 1[n] y 2[n] y 3[n] y 4[n] 33

Overlap and Save x 0[n] convolução Bloco errado x 1[n] h[n] x 2[n] x 3[n] x 4[n] Convolução circular implementada com a FFT aliasing (x 0[n]|x 1[n])*h[n] (x 1[n]|x 2[n])*h[n] Bloco correcto y 0[n] (x 2[n]|x 3[n])*h[n] Save y 1[n] y 2[n] y 3[n] y 4[n] 34