A Total Error Framework for Hybrid Estimation Paul

A Total Error Framework for Hybrid Estimation Paul P. Biemer 1, 2 Asley Amaya 1 1 RTI International 2 University of North Carolina at Chapel Hill BIGSURV 18 Barcelona, Spain October 26, 2018 RTI International is a registered trademark and a trade name of Research Triangle Institute. www. rti. org

Outline § Total error framework for the mean of some data set Simple dichotomous decomposition – More complex decompositions for error source targeting – Mathematical formulation of concepts § Expression for the “Total” Mean Squared Error of the unweighted data set mean § Illustration comparing a small random sample with a large census § Data weighting and other error mitigation strategies § 2

Generalized TE Framework Total Error = Sample Recruitment Error + Data Encoding Error Sample Recruitment Error is a generalization of the concept of representation error Data Encoding Error is a generalization of the concept of measurement error 3

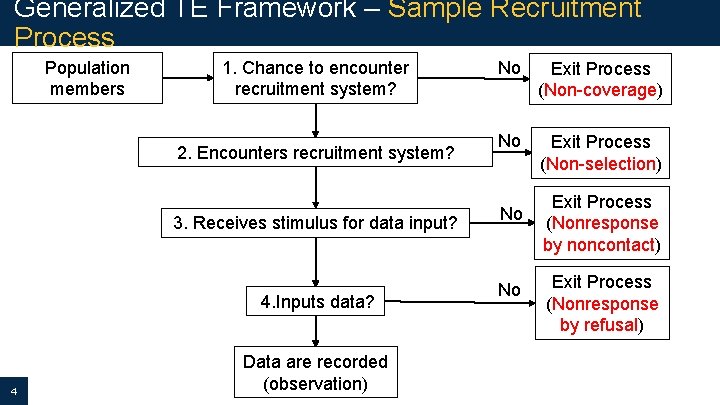
Generalized TE Framework – Sample Recruitment Process Population members 1. Chance to encounter recruitment system? 2. Encounters recruitment system? 3. Receives stimulus for data input? 4. Inputs data? 4 Data are recorded (observation) No Exit Process (Non-coverage) No Exit Process (Non-selection) No No Exit Process (Nonresponse by noncontact) Exit Process (Nonresponse by refusal)

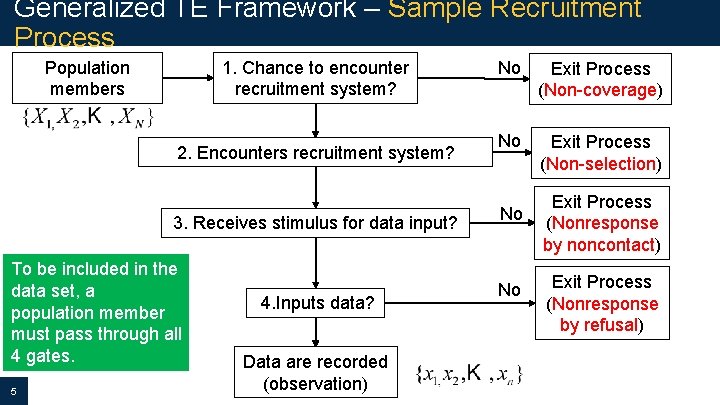
Generalized TE Framework – Sample Recruitment Process Population members 1. Chance to encounter recruitment system? 2. Encounters recruitment system? 3. Receives stimulus for data input? To be included in the data set, a population member must pass through all 4 gates. 5 4. Inputs data? Data are recorded (observation) No Exit Process (Non-coverage) No Exit Process (Non-selection) No No Exit Process (Nonresponse by noncontact) Exit Process (Nonresponse by refusal)

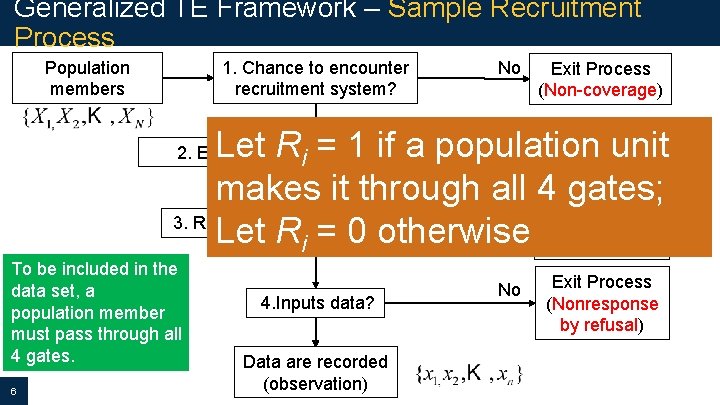
Generalized TE Framework – Sample Recruitment Process Population members 1. Chance to encounter recruitment system? No Exit Process (Non-coverage) No Exit Process Let R = 1 if a population unit (Non-selection) makes it through all 4 Exitgates; Process No (Nonresponse 3. Receives stimulus for data input? Let Ri = 0 otherwise by noncontact) 2. Encounters recruitment system? i To be included in the data set, a population member must pass through all 4 gates. 6 4. Inputs data? Data are recorded (observation) No Exit Process (Nonresponse by refusal)

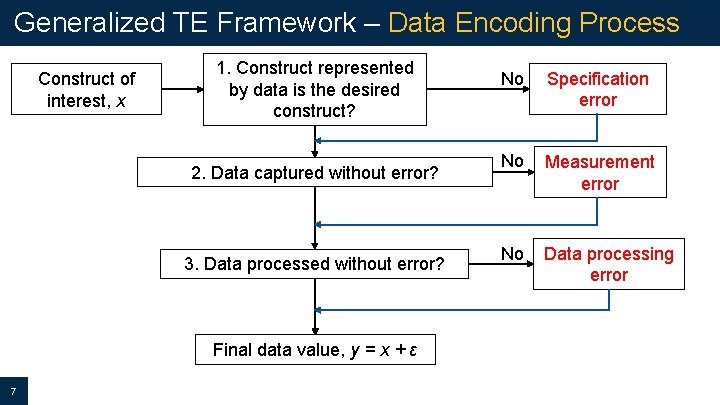
Generalized TE Framework – Data Encoding Process Construct of interest, x 1. Construct represented by data is the desired construct? 2. Data captured without error? 3. Data processed without error? Final data value, y = x + ε 7 No Specification error No Measurement error No Data processing error

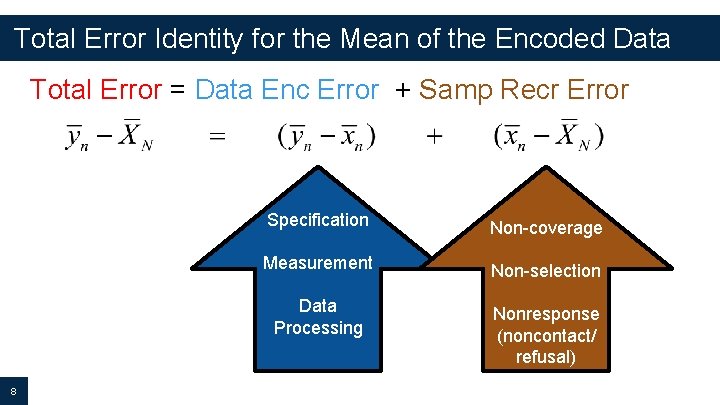
Total Error Identity for the Mean of the Encoded Data Total Error = Data Enc Error + Samp Recr Error 8 Specification Non-coverage Measurement Non-selection Data Processing Nonresponse (noncontact/ refusal)

Data Encoding Error xi is the true characteristic for the ith sample unit § yi is the encoded value of xi § εi = yi - xi is the error in the encoded value for the ith sample unit – Assume εi ~ i. i. d (Bε , ) § 9 Data capture error bias Data capture error variance

Sample Recruitment Error (or Errors of Nonobservation) Xi denotes the characteristic measured for the ith person in the Recruitment Process § , a measure of selection bias § Population variance Bias induced by the data capture process Meng, 2017; Bethlehem, 1988 10

Sample Recruitment Error Xi denotes the characteristic measured for the ith person in the Recruitment Process § , a measure of selection bias § Example: For SRS sampling and no nonresponse, 11

Total Mean Squared Error of the Mean of a Generic Data Set Total Error = Data Enc Error + Samp Recr Error 12 Bias from Variance from • Specification error • Measurement error • Data processing error Variance & Bias from • Noncoverage • Nonselection • Nonresponse Recording error/capture error interaction

Interpretation of Not much is known about ρRX for nonprobability samples. § However, ρRX has been studied extensively for surveys (through the estimation of nonresponse bias). § ρRX will be smaller for nonprobability samples when gates 1, 2 and 3 are entered for all members of the population. § Ability to adjust for sample recruitment bias is better for surveys because § We have more control over who enters gates 1 -3 and thus more control over ρRX – We often know a lot about sample recruitment failures and how to adjust for them through weighting and imputation. – 13

Illustration of Some Uses of these Results? Which is more accurate? An estimate of the population average based upon an administrative data set with almost 100, 000 population records and over 80% coverage? or 2. A national survey estimate based upon probability sample of size 3, 300 completed cases with a 55% response rate? 1. 14

We try to answer this question for the US Residential Energy Consumption Survey (RECS) § Survey Data: 2015 RECS Mode changed from face to web/mail – Respondent reports of housing unit square footage not reliable – Substituting administrative data could be more accurate – response rate ≈ 55% – n ≈ 6, 000*. 55 = 3, 300 completed cases – § Administrative data: Zillow real estate data base Coverage ≈ 82% – n ≈ 100, 000 records – Other data bases were also considered (Acxiom and Core. Logic) – 15

We try to answer this question for the US Residential Energy Consumption Survey (RECS) § § § 16 HU square footage is primarily used for micro-econometric modeling We will consider estimation of the U. S. average HU square footage to demonstrate the MSE analysis Similar analysis could be considered for other parameters of interest (i. e. , regression coefficients) However, the current formulation would not be appropriate. Our analysis will use results from Amaya (2017)

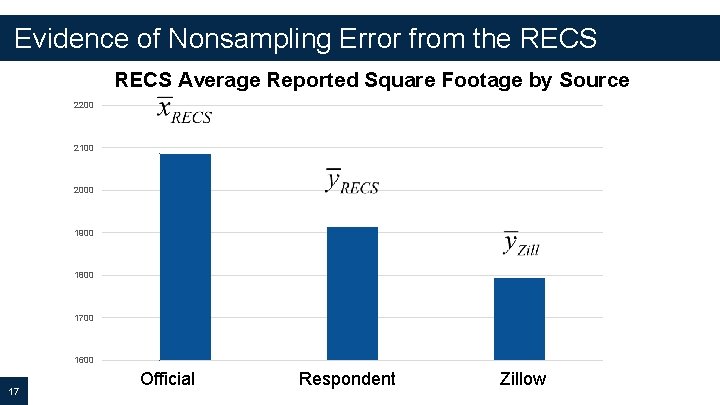
Evidence of Nonsampling Error from the RECS Average Reported Square Footage by Source 2200 2100 2000 1900 1800 1700 1600 17 Official Respondent Zillow

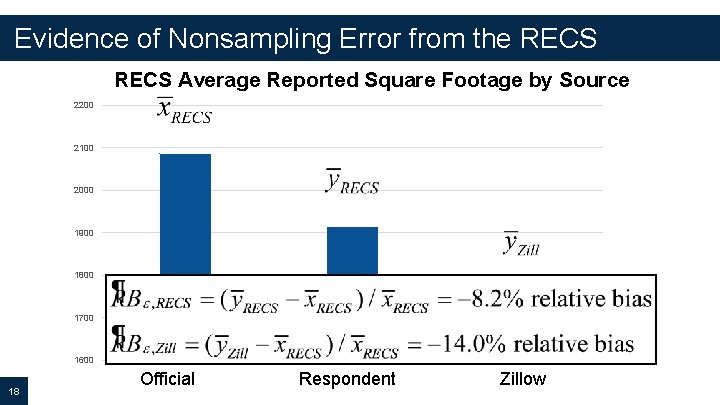
Evidence of Nonsampling Error from the RECS Average Reported Square Footage by Source 2200 2100 2000 1900 1800 1700 1600 18 Official Respondent Zillow

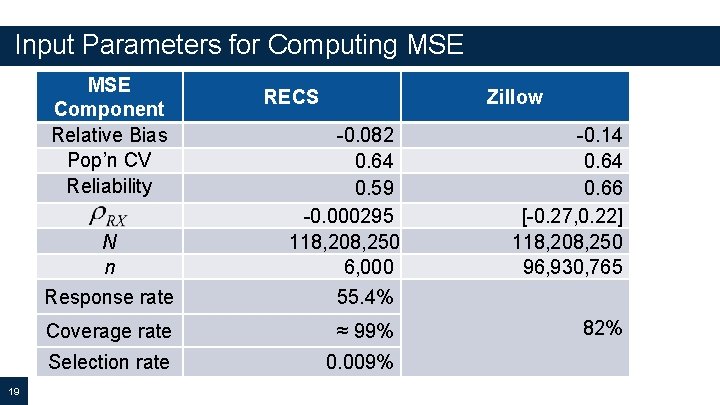
Input Parameters for Computing MSE Component Relative Bias Pop’n CV Reliability N n Response rate 19 RECS Zillow -0. 082 0. 64 0. 59 -0. 000295 118, 208, 250 6, 000 55. 4% Coverage rate ≈ 99% Selection rate 0. 009% -0. 14 0. 66 [-0. 27, 0. 22] 118, 208, 250 96, 930, 765 82%

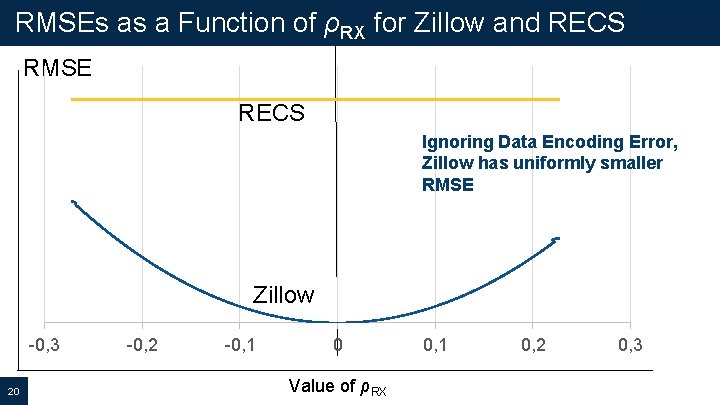
RMSEs as a Function of ρRX for Zillow and RECS RMSE RECS Ignoring Data Encoding Error, Zillow has uniformly smaller RMSE Zillow -0, 3 20 -0, 2 -0, 1 0 Value of ρRX 0, 1 0, 2 0, 3

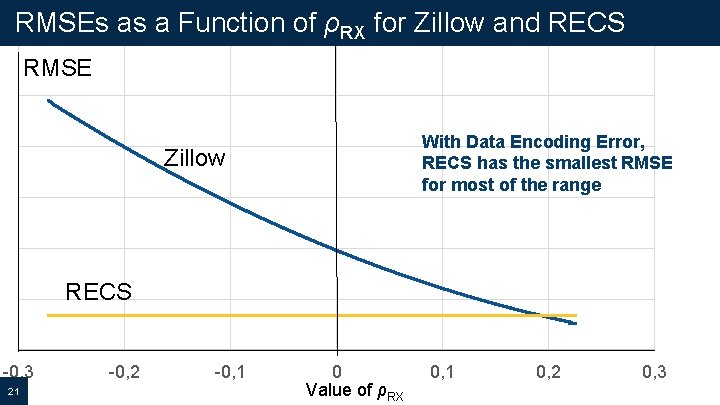
RMSEs as a Function of ρRX for Zillow and RECS RMSE With Data Encoding Error, RECS has the smallest RMSE for most of the range Zillow RECS -0, 3 21 -0, 2 -0, 1 0 Value of ρRX 0, 1 0, 2 0, 3

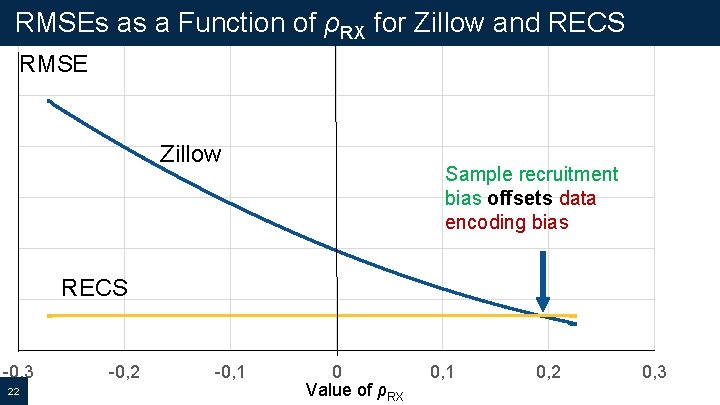
RMSEs as a Function of ρRX for Zillow and RECS RMSE Zillow Sample recruitment bias offsets data encoding bias RECS -0, 3 22 -0, 1 0 Value of ρRX 0, 1 0, 2 0, 3

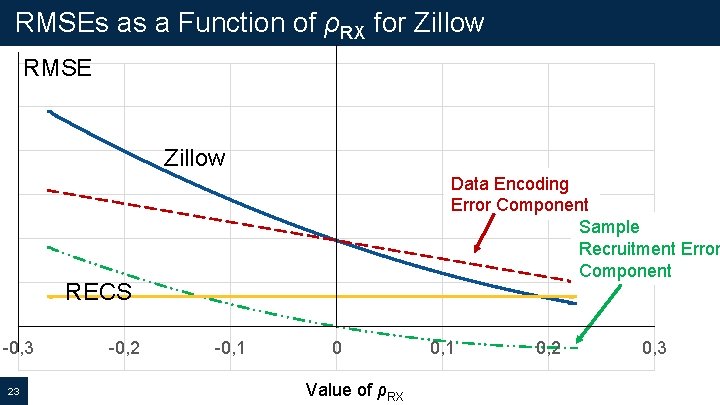
RMSEs as a Function of ρRX for Zillow RMSE Zillow Data Encoding Error Component Sample Recruitment Error Component RECS -0, 3 23 -0, 2 -0, 1 0 Value of ρRX 0, 1 0, 2 0, 3

Results Summary Whether RMSEZillow < RMSERECS depends on value of ρRX § In this case, reducing ρRX may lead to larger RMSE because two biases are offsetting one another § Ideally, both biases should be minimized because an offsetting biases situation is not sustainable § 24

Potential Zillow Error Mitigation Strategies Data Encoding Error § Estimate the bias and adjust for it § May need ground truth square footage data to model this bias Sample Recruitment Error § Weight the Zillow data to reduce |ρRX| § Weights will approximate [E(Ri)]-1 § Modeling E(Ri|X) will require understanding how Ri varies by housing unit and other characteristics (X) of the sample recruitment process 25

A Few Take Aways § As we move towards integrating survey and Big Data, need to consider the total error. Sample recruitment bias is the least understood component of the total error. – Understanding this component will lead to statistical products of greater quality, utility and efficiency. – Focusing solely on data missingness may substantially underestimate total uncertainty. In this illustration, data encoding error dominated the MSE. § The monograph paper will further explore error mitigation strategies for dealing with both data encoding and sample recruitment error. § 26