A thermal radiation model for numerical simulation of

A thermal radiation model for numerical simulation of reacting fluidized beds with MFi. X-TFM, MFi. X-DEM and MFi. X-PIC Michael Stoellinger V M Krushnarao Kotteda Postdoc, Mechanical Engineering Assistant Professor, Mechanical Engineering NETL 2019 Workshop On Multiphase Flow Science, August 6 -8, Morgantown WV

Outline • Introduction • Objectives • Modeling approach • Framework • Test cases- Verification and Validation • Results • Concluding Remarks 2

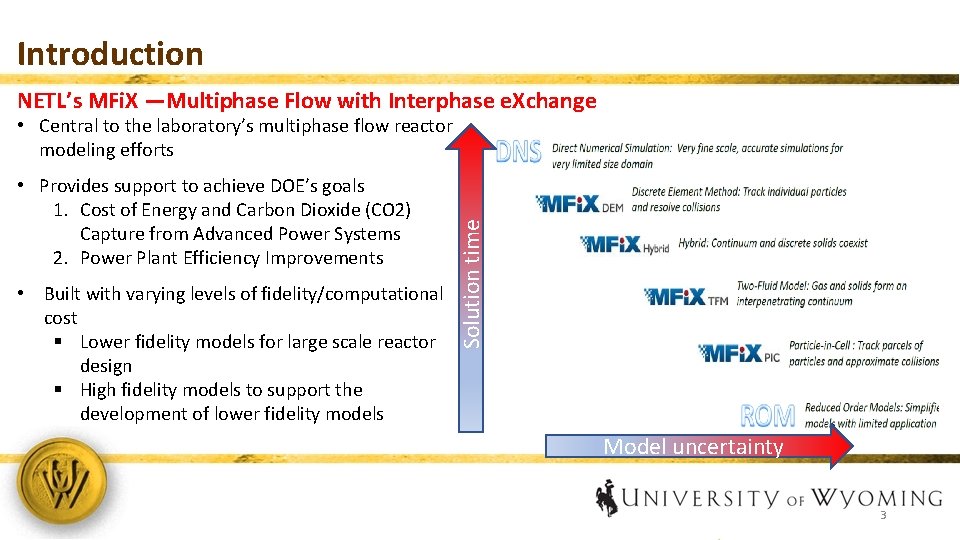
Introduction NETL’s MFi. X —Multiphase Flow with Interphase e. Xchange • Provides support to achieve DOE’s goals 1. Cost of Energy and Carbon Dioxide (CO 2) Capture from Advanced Power Systems 2. Power Plant Efficiency Improvements • Built with varying levels of fidelity/computational cost § Lower fidelity models for large scale reactor design § High fidelity models to support the development of lower fidelity models Solution time • Central to the laboratory’s multiphase flow reactor modeling efforts Model uncertainty 3

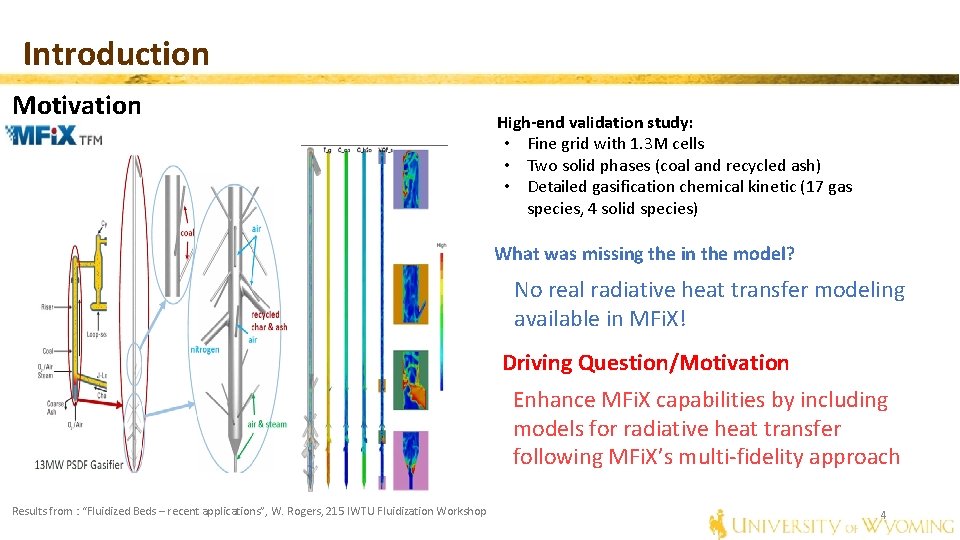
Introduction Motivation High-end validation study: • Fine grid with 1. 3 M cells • Two solid phases (coal and recycled ash) • Detailed gasification chemical kinetic (17 gas species, 4 solid species) What was missing the in the model? No real radiative heat transfer modeling available in MFi. X! Driving Question/Motivation Enhance MFi. X capabilities by including models for radiative heat transfer following MFi. X’s multi-fidelity approach Results from : “Fluidized Beds – recent applications”, W. Rogers, 215 IWTU Fluidization Workshop 4

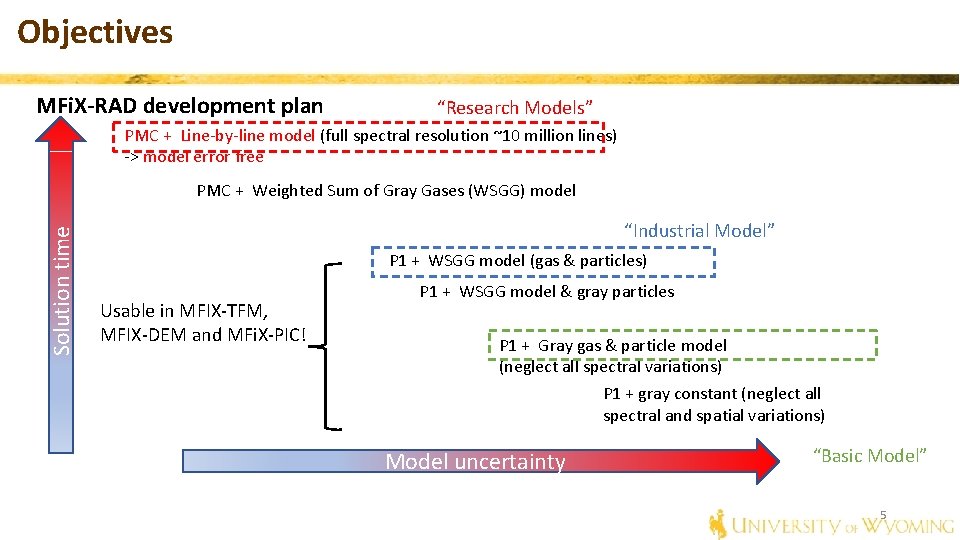
Objectives MFi. X-RAD development plan “Research Models” PMC + Line-by-line model (full spectral resolution ~10 million lines) -> model error free Solution time PMC + Weighted Sum of Gray Gases (WSGG) model “Industrial Model” P 1 + WSGG model (gas & particles) Usable in MFIX-TFM, MFIX-DEM and MFi. X-PIC! P 1 + WSGG model & gray particles P 1 + Gray gas & particle model (neglect all spectral variations) P 1 + gray constant (neglect all spectral and spatial variations) Model uncertainty “Basic Model” 5

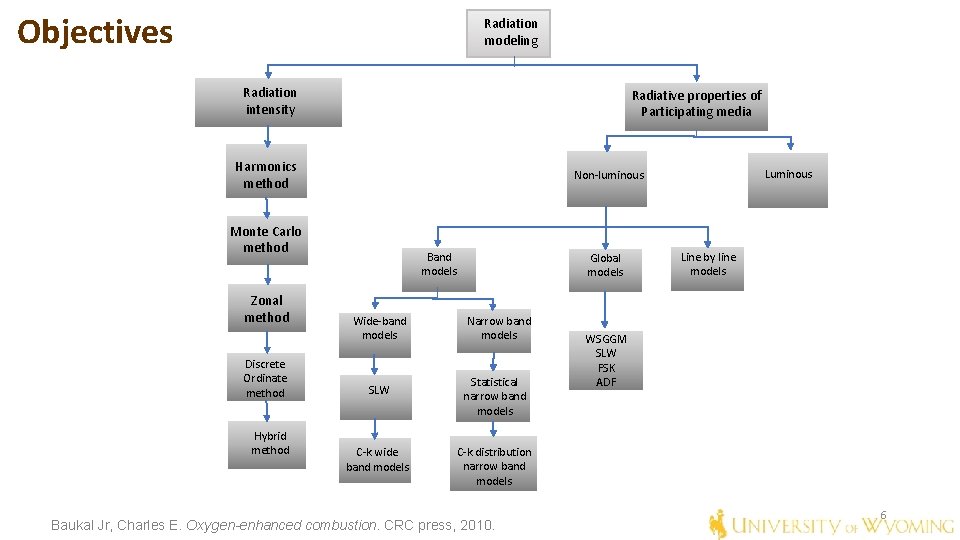
Objectives Radiation modeling Radiation intensity Radiative properties of Participating media Harmonics method Monte Carlo method Zonal method Discrete Ordinate method Hybrid method Luminous Non-luminous Band models Wide-band models SLW C-k wide band models Global models Narrow band models Statistical narrow band models Line by line models WSGGM SLW FSK ADF C-k distribution narrow band models Baukal Jr, Charles E. Oxygen-enhanced combustion. CRC press, 2010. 6

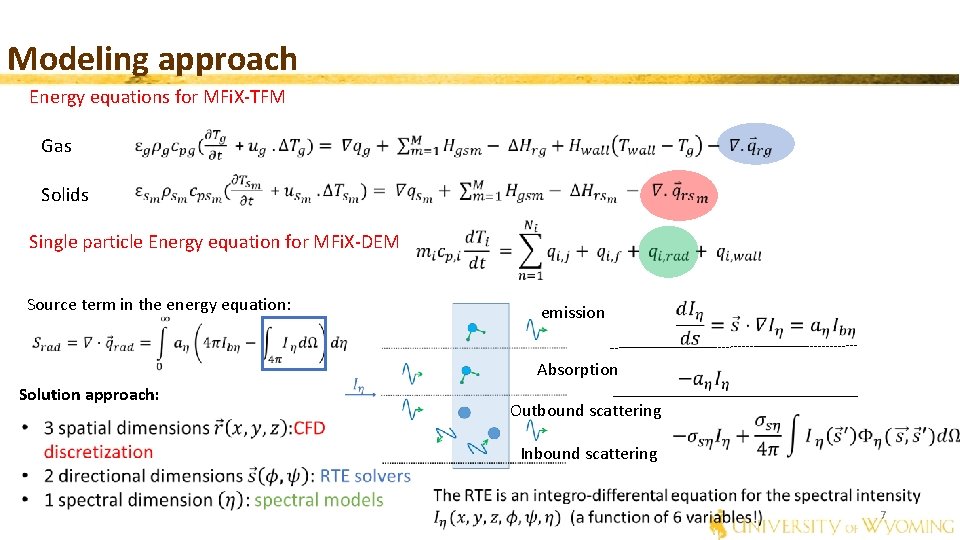
Modeling approach Energy equations for MFi. X-TFM Gas Solids Single particle Energy equation for MFi. X-DEM Source term in the energy equation: emission Absorption Solution approach: Outbound scattering Inbound scattering 7

Modeling approach Gray P 1 model assumptions Spherical harmonics Spatially varying coefficients 4) Solve a “combined” (including all phases) P 1 equation for G (Helmholtz type) Gas phase absorption Solid phase absorption Gas phase emission Solid phases emission 8

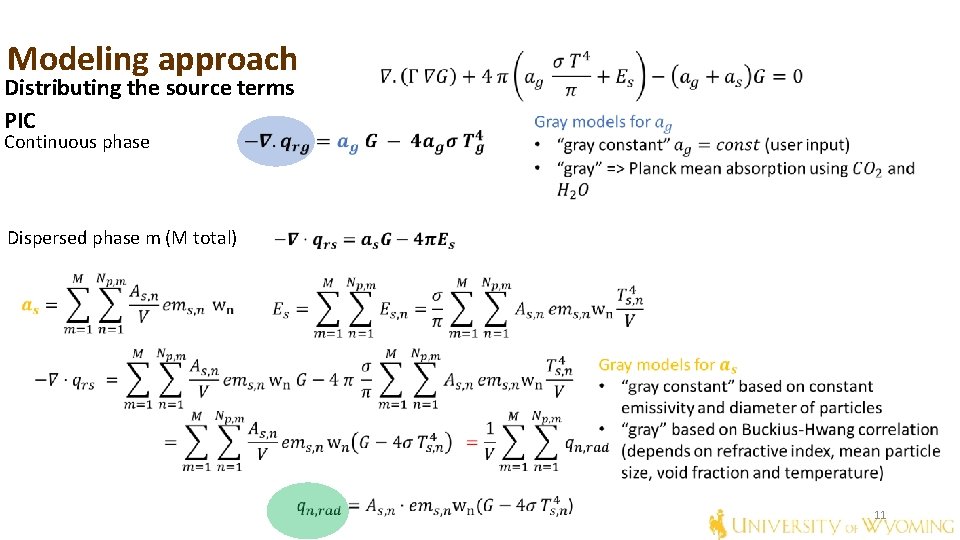
Modeling approach Distributing the source terms TFM Continuous phase Dispersed phase m (M total) 9

Modeling approach Distributing the source terms DEM Continuous phase Dispersed phase m (M total) DEM source terms 10

Modeling approach Distributing the source terms PIC Continuous phase Dispersed phase m (M total) 11

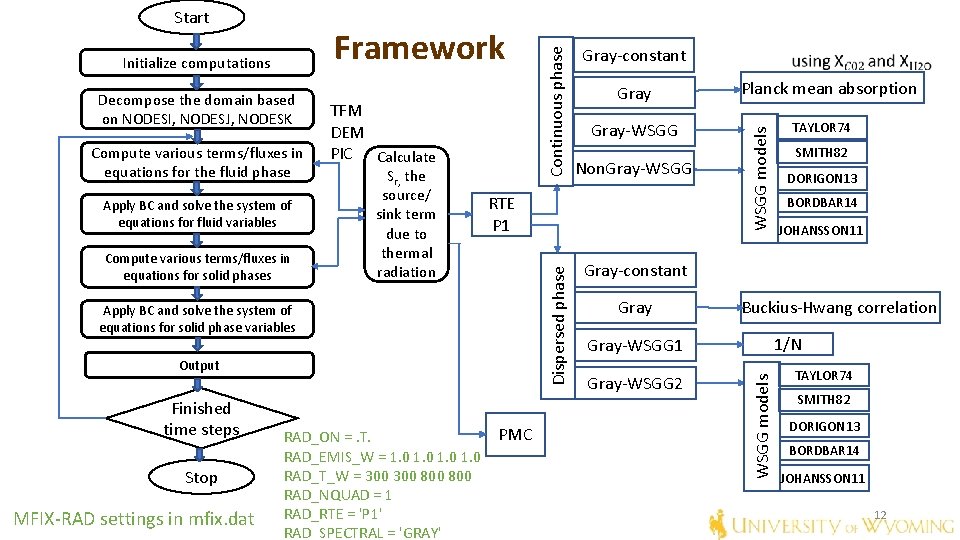
Apply BC and solve the system of equations for fluid variables Compute various terms/fluxes in equations for solid phases Sr, the source/ sink term due to thermal radiation Output Stop MFIX-RAD settings in mfix. dat RAD_ON =. T. RAD_EMIS_W = 1. 0 RAD_T_W = 300 800 RAD_NQUAD = 1 RAD_RTE = 'P 1' RAD_SPECTRAL = 'GRAY' Gray-WSGG Non. Gray-WSGG RTE P 1 Apply BC and solve the system of equations for solid phase variables Finished time steps Gray PMC Planck mean absorption WSGG models Compute various terms/fluxes in equations for the fluid phase TFM DEM PIC Calculate Dispersed phase Decompose the domain based on NODESI, NODESJ, NODESK Gray-constant TAYLOR 74 SMITH 82 DORIGON 13 BORDBAR 14 JOHANSSON 11 Gray-constant Gray Buckius-Hwang correlation 1/N Gray-WSGG 1 Gray-WSGG 2 WSGG models Framework Initialize computations Continuous phase Start TAYLOR 74 SMITH 82 DORIGON 13 BORDBAR 14 JOHANSSON 11 12

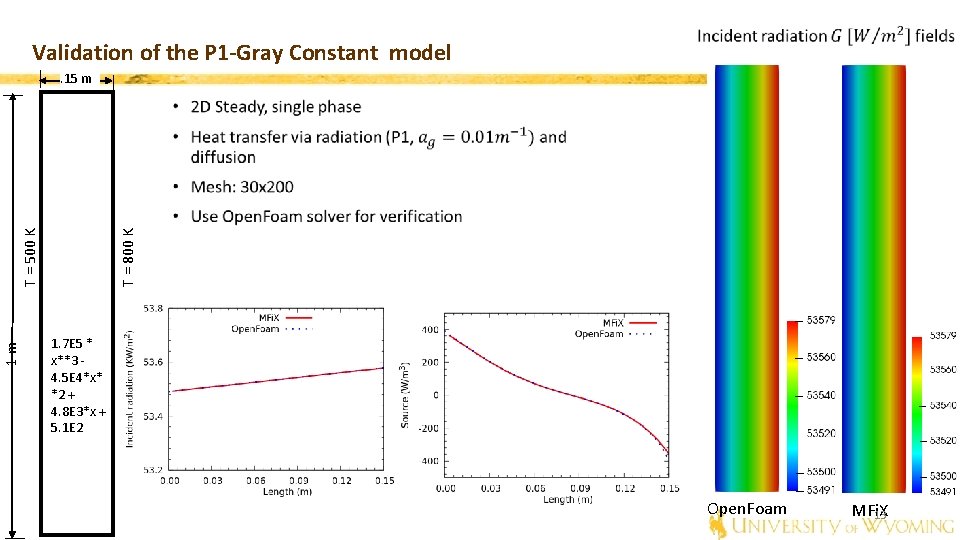
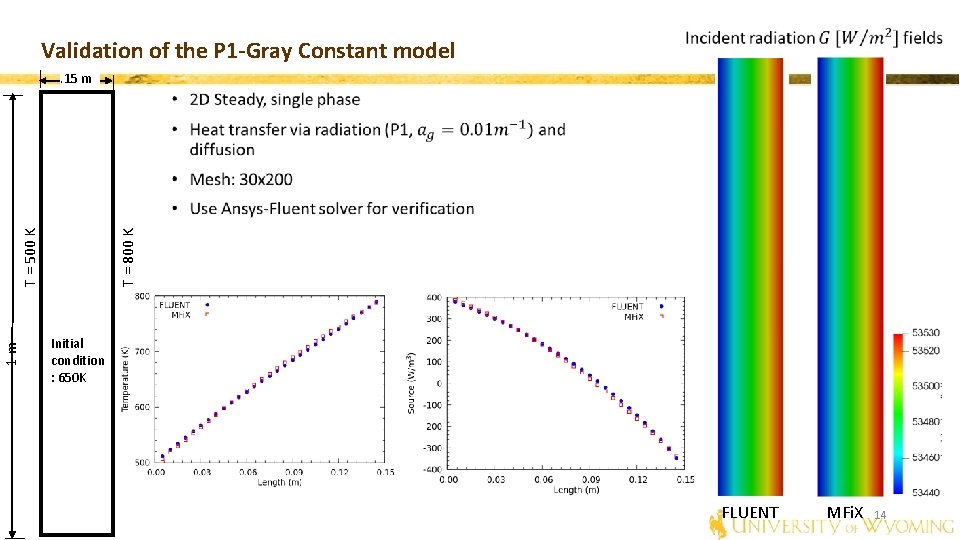
Validation of the P 1 -Gray Constant model . 15 m 1 m T = 800 K T = 500 K 1. 7 E 5 * x**3 - 4. 5 E 4*x* *2 + 4. 8 E 3*x + 5. 1 E 2 Open. Foam MFi. X 13

Validation of the P 1 -Gray Constant model . 15 m 1 m T = 800 K T = 500 K Initial condition : 650 K FLUENT MFi. X 14

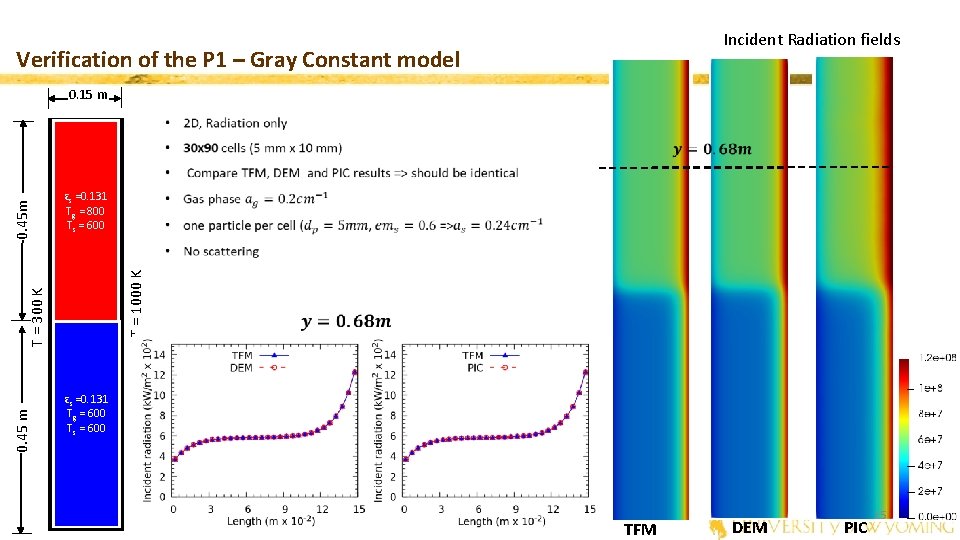
Incident Radiation fields Verification of the P 1 – Gray Constant model 0. 15 m T = 1000 K εs =0. 131 Tg = 800 Ts = 600 0. 45 m T = 300 K 0. 45 m εs =0. 131 Tg = 600 Ts = 600 TFM DEM PIC 15

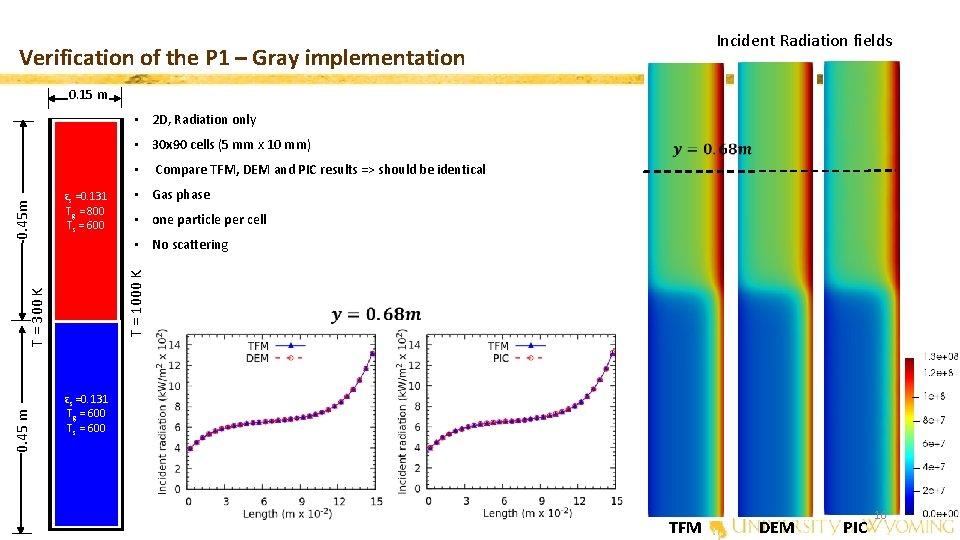
Incident Radiation fields Verification of the P 1 – Gray implementation 0. 15 m • 2 D, Radiation only • 30 x 90 cells (5 mm x 10 mm) εs =0. 131 Tg = 800 Ts = 600 0. 45 m • Gas phase • one particle per cell T = 1000 K • No scattering T = 300 K 0. 45 m • Compare TFM, DEM and PIC results => should be identical εs =0. 131 Tg = 600 Ts = 600 TFM DEM PIC 16

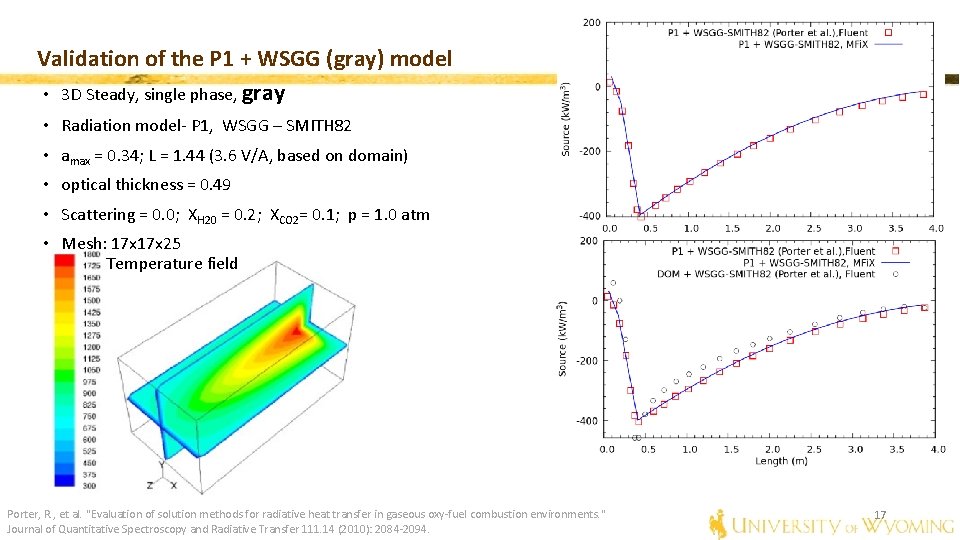
Validation of the P 1 + WSGG (gray) model • 3 D Steady, single phase, gray • Radiation model- P 1, WSGG – SMITH 82 • amax = 0. 34; L = 1. 44 (3. 6 V/A, based on domain) • optical thickness = 0. 49 • Scattering = 0. 0; XH 20 = 0. 2; XCO 2= 0. 1; p = 1. 0 atm • Mesh: 17 x 25 Temperature field Porter, R. , et al. "Evaluation of solution methods for radiative heat transfer in gaseous oxy-fuel combustion environments. " Journal of Quantitative Spectroscopy and Radiative Transfer 111. 14 (2010): 2084 -2094. 17

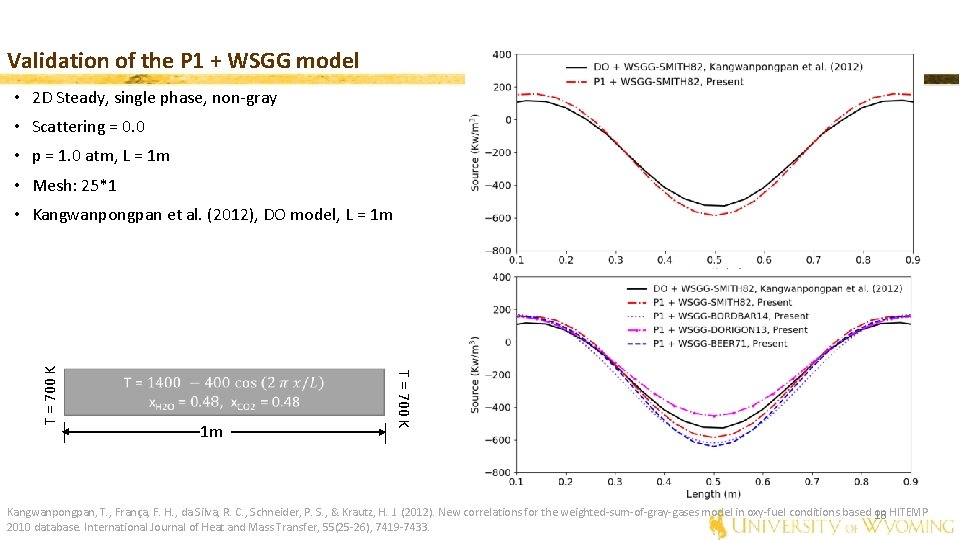
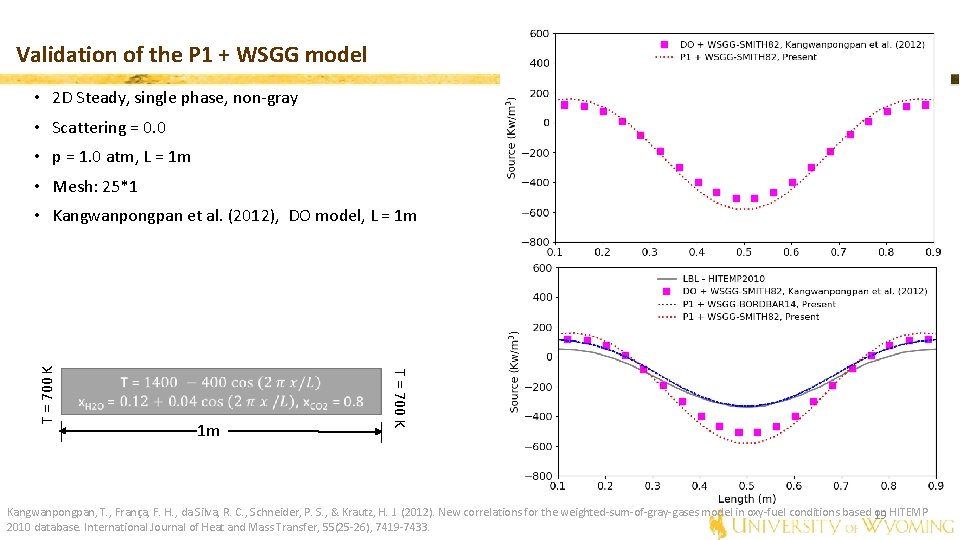
Validation of the P 1 + WSGG model • 2 D Steady, single phase, non-gray • Scattering = 0. 0 • p = 1. 0 atm, L = 1 m • Mesh: 25*1 1 m T = 700 K • Kangwanpongpan et al. (2012), DO model, L = 1 m Kangwanpongpan, T. , França, F. H. , da Silva, R. C. , Schneider, P. S. , & Krautz, H. J. (2012). New correlations for the weighted-sum-of-gray-gases model in oxy-fuel conditions based on HITEMP 18 2010 database. International Journal of Heat and Mass Transfer, 55(25 -26), 7419 -7433.

Validation of the P 1 + WSGG model • 2 D Steady, single phase, non-gray • Scattering = 0. 0 • p = 1. 0 atm, L = 1 m • Mesh: 25*1 1 m T = 700 K • Kangwanpongpan et al. (2012), DO model, L = 1 m Kangwanpongpan, T. , França, F. H. , da Silva, R. C. , Schneider, P. S. , & Krautz, H. J. (2012). New correlations for the weighted-sum-of-gray-gases model in oxy-fuel conditions based on HITEMP 19 2010 database. International Journal of Heat and Mass Transfer, 55(25 -26), 7419 -7433.

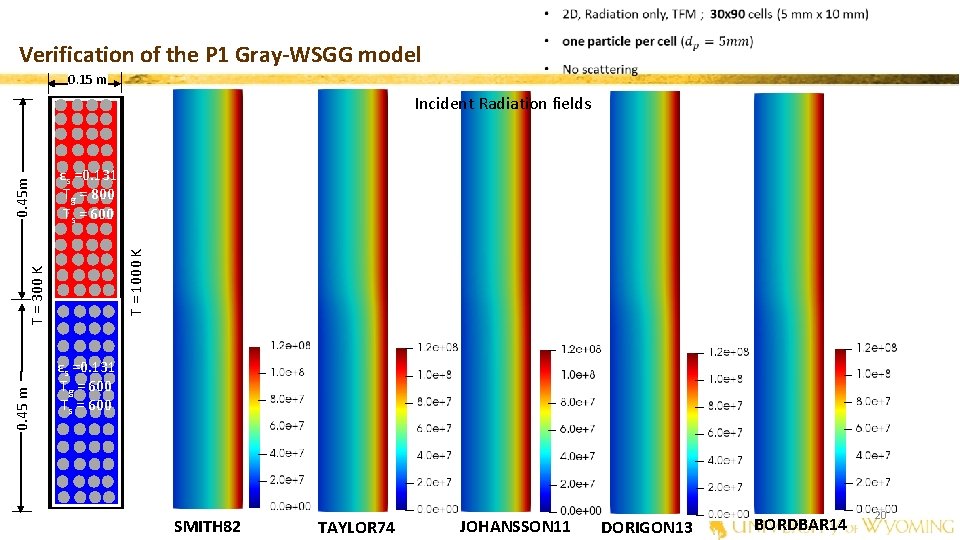
Verification of the P 1 Gray-WSGG model 0. 15 m T = 1000 K εs =0. 131 Tg = 800 Ts = 600 0. 45 m T = 300 K 0. 45 m Incident Radiation fields εs =0. 131 Tg = 600 Ts = 600 SMITH 82 TAYLOR 74 JOHANSSON 11 DORIGON 13 BORDBAR 14 20

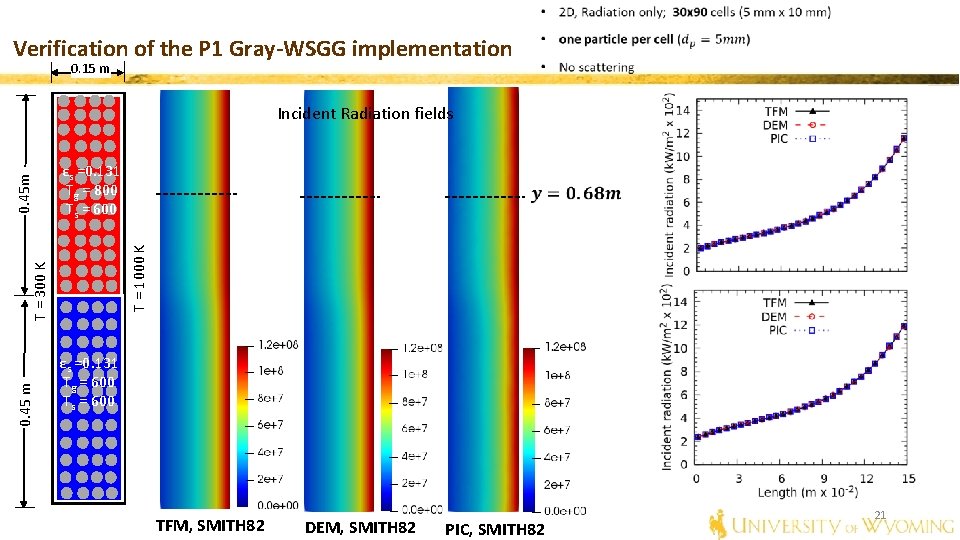
Verification of the P 1 Gray-WSGG implementation 0. 15 m εs =0. 131 Tg = 800 Ts = 600 0. 45 m T = 1000 K T = 300 K 0. 45 m Incident Radiation fields εs =0. 131 Tg = 600 Ts = 600 TFM, SMITH 82 DEM, SMITH 82 PIC, SMITH 82 21

r=10 cm Relevance of thermal radiation in Lab-Scale reactors (54 k. Wth) Gas & solid phase reactions 2*CO --> Soot + CO 2 CO + 0. 5*O 2 --> CO 2 2*FC 1 + O 2 --> 2*CO FC 1 + CO 2 --> 2*CO 2*FC 2 + O 2 --> 2*CO FC 2 + CO 2 --> 2*CO FC 2 --> FC 1 Ash 2 --> Ash 1 Air 300 K, 4 g/s Char 300 K 1. 8 g/s H=60 cm Compare results with and without radiative heat transfer! Air 300 K, 11. 6 g/s 22

Relevance of thermal radiation in Lab-Scale reactors (54 k. Wth) Gas Temperature [K] Gas volume fraction Mass weighted average temperatures at the outlet Even in low-Temp Lab scale reactor! No rad P 1 gray 23

Concluding Remarks 24

Acknowledgement Thank you 25

Gas volume fraction Time : 16. 0 Gas Temperature [K] Time : 16. 0 Solid Temperature [K] Average temperatures at the outlet Time : 16. 0 26