A Theory of Predicatecomplete Test Coverage and Generation

A Theory of Predicate-complete Test Coverage and Generation Thomas Ball Testing, Verification and Measurement Microsoft Research FMCO Symposium November 2 -5 2004

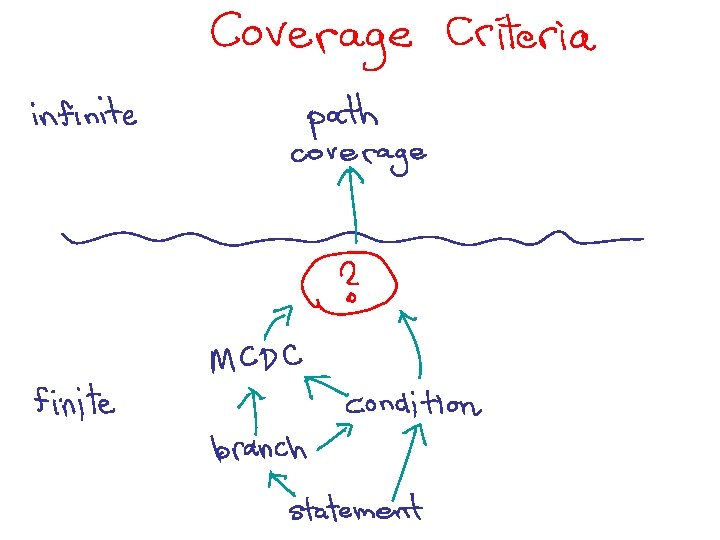
Control-flow Coverage Criteria • Statement/branch coverage widely used in industry • 100% coverage ≠ a bug-free program!! • More stringent criteria – modified-condition-decision, predicate, dataflow, mutation, path, …

Beyond Statement and Branch Coverage void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; while (lo<=hi) { while (a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }

Beyond Statement and Branch Coverage void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; while (lo<=hi) { while (a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }

Beyond Statement and Branch Coverage void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; while (lo<=hi) { while (a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }

Corrected Program void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; while (lo<=hi) { while (lo<=hi && a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }

Corrected Program void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; while (lo<=hi) { while (lo<=hi && a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }

Predicate-complete Testing • Program predicates – relational expression such as (x<0) – the expression (x<0) || (y>0) has two predicates • Program with m statements and n predicates – m x 2 n possible observable states S – finest partition of behavior based on programmer’s observations • Goal – cover all reachable observable states R S

Reachable Observable States L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

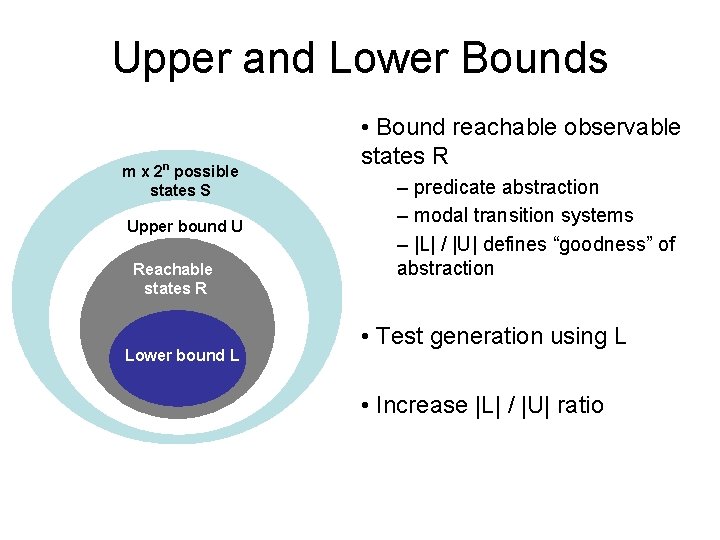
Upper and Lower Bounds m x 2 n possible states S Upper bound U Reachable states R Lower bound L • Bound reachable observable states R – predicate abstraction – modal transition systems – |L| / |U| defines “goodness” of abstraction • Test generation using L • Increase |L| / |U| ratio

Overview • • • Upper and lower bounds Example Test case generation Refinement Discussion Conclusions

Predicate Abstraction of Infinite-state Systems – Graf & Saïdi, CAV ’ 97 – Abstract Interpretation, Cousot & Cousot ‘ 77 • Idea – Given set of predicates P = { P 1, …, Pk } • Formulas describing properties of system state • Abstract State Space – Set of Abstract Boolean variables B = { b 1, …, bk } • bi = true Set of states where Pi holds

Modal Transitions [Larsen] MC MA a may total a’ a’ a a total & onto a’ a’

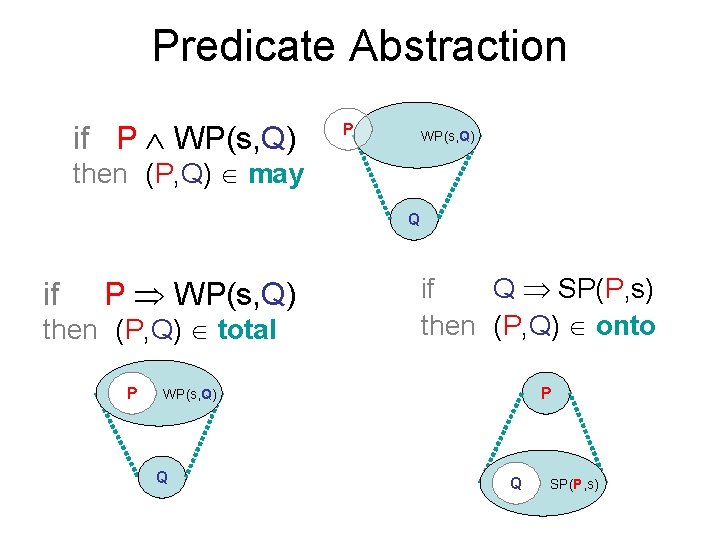
Predicate Abstraction if P WP(s, Q) P WP(s, Q) then (P, Q) may Q if P WP(s, Q) then (P, Q) total P if Q SP(P, s) then (P, Q) onto P WP(s, Q) Q Q SP(P, s)

Example

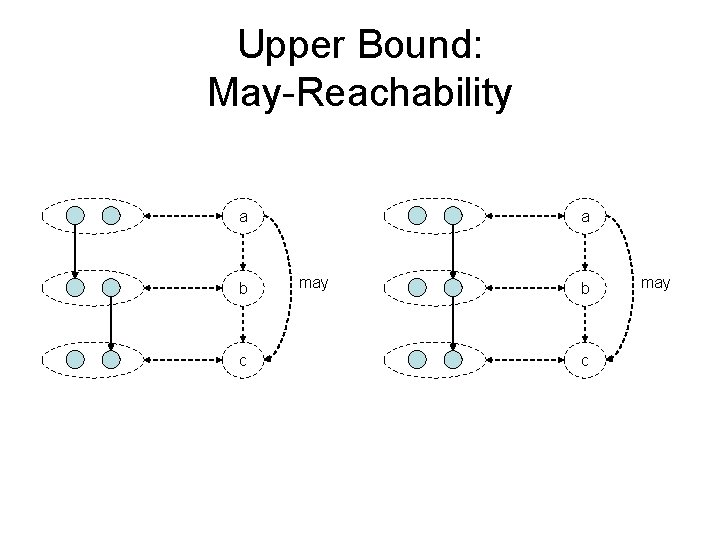
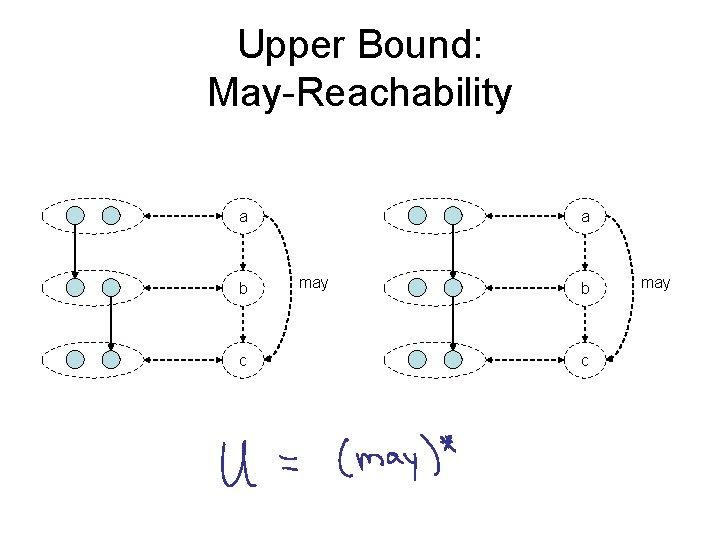
Upper Bound: May-Reachability a b c a may b c may

Upper Bound: May-Reachability a b c a may b c may

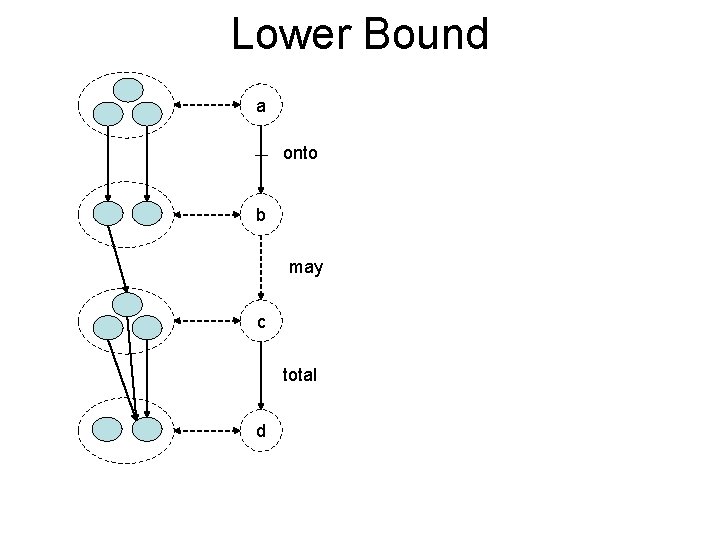
Lower Bound a onto b may c total d

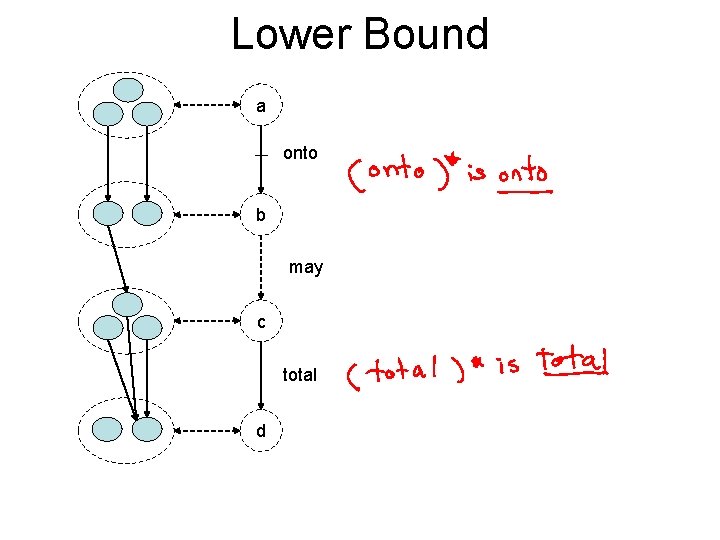
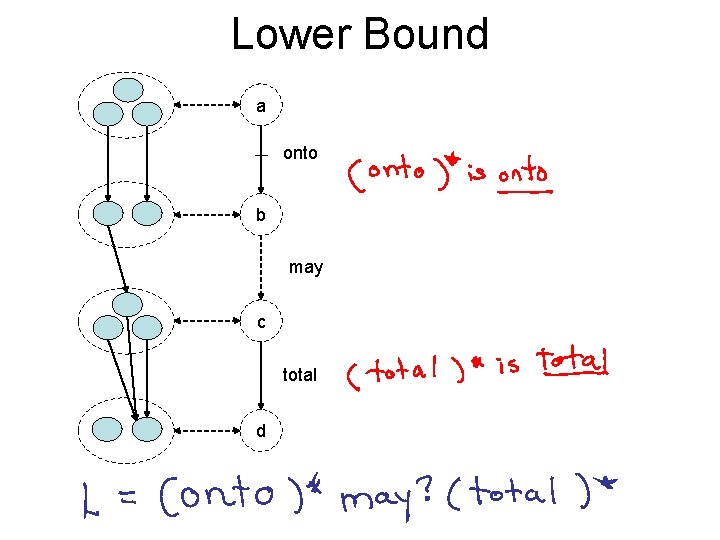
Lower Bound a onto b may c total d

Lower Bound a onto b may c total d

Overview • • • Upper and lower bounds Example Test case generation Refinement Discussion Conclusions

Example void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; while (lo<=hi) { while (a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }

Observation Vector [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] • lo<hi lo<=hi • lo<hi lo<=hi (a[lo]<=pivot a[hi]>pivot) ( a[lo]<=pivot a[hi]>pivot) Only 10/16 observations possible

void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; L 0: while (lo<=hi) { L 1: ; L 2: while (a[lo]<=pivot) { L 3: lo++; L 4: ; } L 5: while (a[hi]>pivot) { L 6: hi--; L 7: ; } L 8: if (lo<hi) { L 9: swap(a, lo, hi); LA: ; } LB: ; } LC: ; } 13 labels x 10 observations = 130 observable states But, program constrains reachable observable states greatly.

Overview • • • Upper and lower bounds Example Test case generation Refinement Discussion Conclusions

Test Generation • DFS of lower bound generates covering set of paths • Symbolically execute paths to generate tests • Run program on tests to find errors and compute coverage of observable states

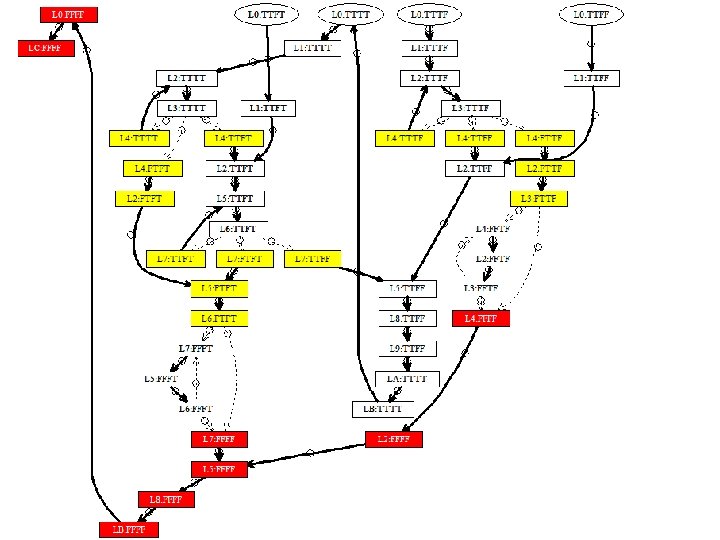
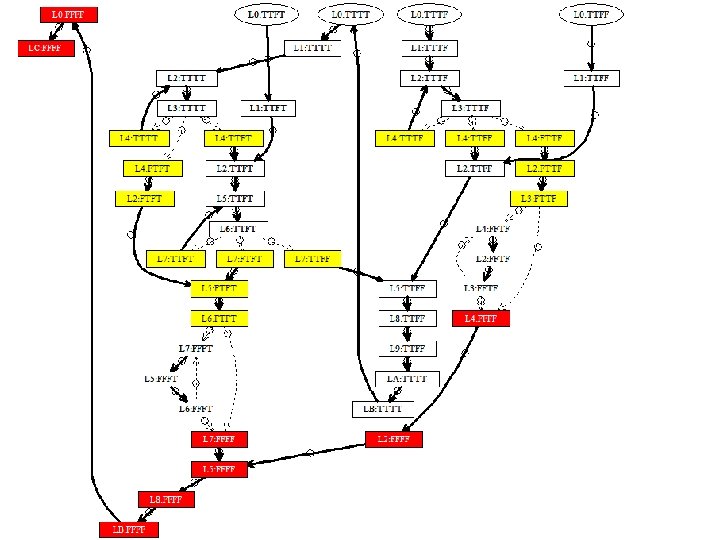
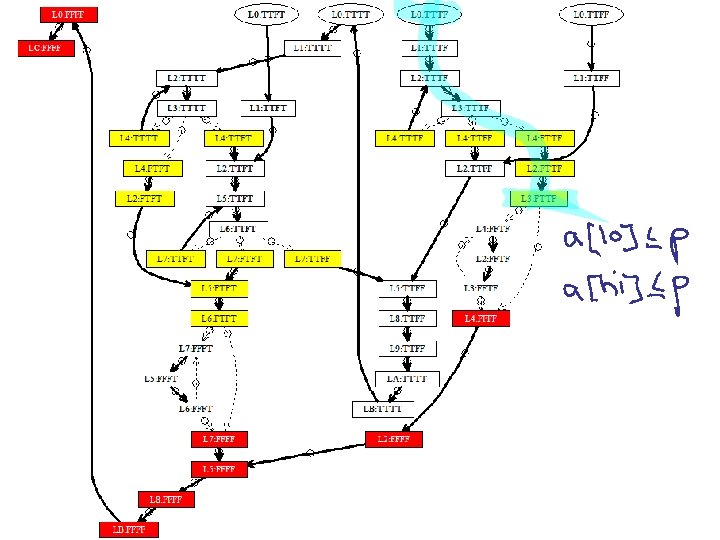
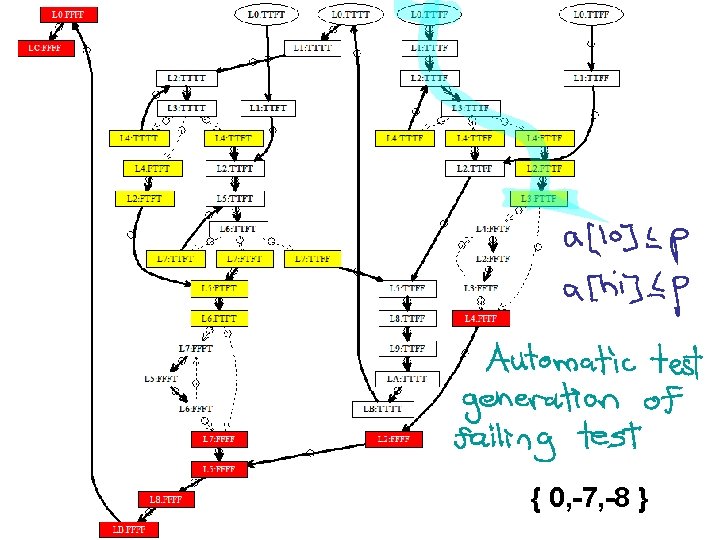
Generated Inputs void partition(int a[]) { assume(a. length>2); int pivot = a[0]; int lo = 1; int hi = a. length-1; Array bounds violations (L 0: TTTT, L 4: FTFT) (L 0: TTTT, L 4: TTTT) while (lo<=hi) { (L 0: TTTF, L 4: TTFF) ; (L 0: TTTF, L 4: FTTF) while (a[lo]<=pivot) { (L 0: TTTF, L 4: TTTF) lo++; (L 0: TTFT, L 7: TTFF) (L 0: TTFT, L 7: FTFT) ; } while (a[hi]>pivot) { (L 0: TTFT, L 7: TTFT) (L 0: TTFF, L 0: TTTT) hi--; L 0: L 1: L 2: L 3: L 4: L 5: L 6: L 7: ; } L 8: if (lo<hi) { L 9: swap(a, lo, hi); LA: ; } LB: ; } LC: ; } { 0, -8, 1 } { 0, -8, 2, 1 } { 0, -8, 1 } { 1, -7, 3, 0 } { 0, -7, -8 } { 1, -7, 0 } { 0, 2, -8, 1 } { 0, 1, 2 } { 0, 3, 1, 2 } { 1, 2, -1, 0 }

Results • Buggy partition function – U=49, L=43, Tested=42 • Fixed partition function – U=56, L=37, Tested=43 • What about the remaining 13 states?

Overview • • • Upper and lower bounds Example Test case generation Refinement Discussion Conclusions

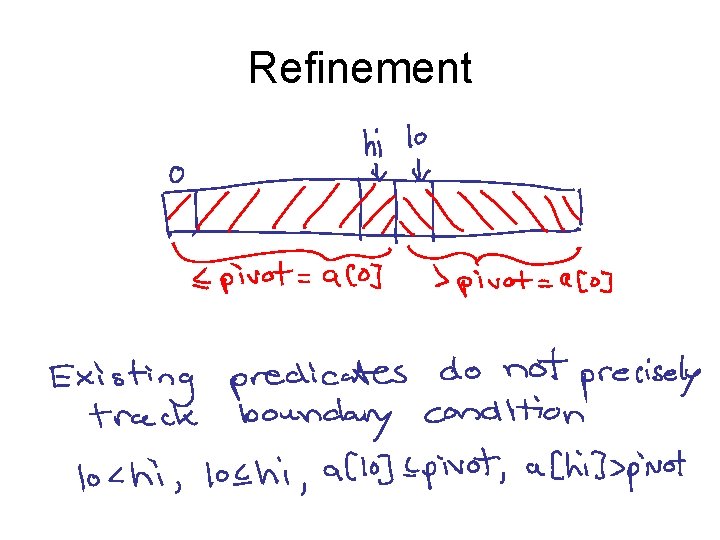
Refinement

New Observation Vector [ lo<hi, lo<=hi, lo=hi+1, a[lo]<=pivot, a[hi]>pivot, a[lo-1]<=pivot, a[hi+1]>pivot ] Only 48/128 observations possible For this set of predicates, L = U

Overview • • • Upper and lower bounds Example Test case generation Refinement Discussion Conclusions

Discussion • Comparison to bisimulation • Completeness of abstractions • Related work

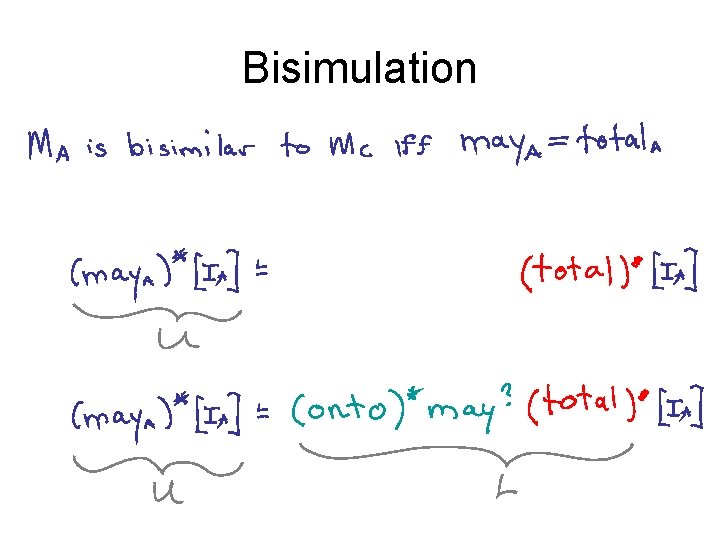
Bisimulation

Bisimulation

Abstraction Completeness

Abstraction Completeness

Related Work • • • Predicate abstraction Modal transition systems Abstraction-guided test generation Symbolic execution/constraint satisfaction Test coverage criteria

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

Path Coverage does not imply PCT Coverage L 1: L 2: L 3: L 4: if (p) if (q) x=0; y=p+q;

Path Coverage does not imply PCT Coverage L 1: L 2: L 3: L 4: if (p) if (q) x=0; y=p+q;

Conclusions • PCT coverage – new form of state-based coverage – similar to path coverage but finite • Upper and lower bounds – computed using predicate abstraction and modal transitions – use lower bound to guide test generation – refine bounds