A Theoretical Model for Learning from Labeled and

A Theoretical Model for Learning from Labeled and Unlabeled Data Maria-Florina Balcan & Avrim Blum Carnegie Mellon University, Computer Science Department Maria-Florina Balcan

What is Machine Learning? • Design of programs that adapt from experience, identify patterns in data. • Used to: – recognize speech, faces, … – categorize documents, info retrieval, . . . • Goals of ML theory: develop models, analyze algorithmic and statistical issues involved. Maria-Florina Balcan

Outline of the talk • Brief Overview of Supervised Learning – PAC Model • Semi-Supervised Learning – An Augmented PAC Style Model Maria-Florina Balcan

Usual Supervised Learning Problem • Decide which email messages are spam and which are important. • Might represent each message by n features. (e. g. , keywords, spelling, etc. ). • Take a sample S of data, labeled according to whether they were/weren't spam. • Goal of algorithm is to use data seen so far to produce good prediction rule h (a "hypothesis") for future data. Maria-Florina Balcan

The Concept Learning Setting E. g. , example label Given data, some reasonable rules might be: • Predict SPAM if unknown AND (money OR pills) • Predict SPAM if money + pills – known > 0 • . . . Maria-Florina Balcan

Supervised Learning, Big Questions • Algorithm Design. How to optimize? – How might we automatically generate rules that do well on observed data? • Sample Complexity/Confidence Bound – Real goal is to do well on new data. – What kind of confidence do we have that rules that do well on sample will do well in the future? • for a given learning alg, how much data do we need. . . Maria-Florina Balcan

Supervised Learning: Formalization (PAC) • PAC model – standard model for learning from labeled data. • Have sample S = {(x, l)} drawn from some distrib D over examples x 2 X, labeled by some target function c*. • Alg does optimization over S to produce some hypothesis h 2 C (e. g. , C = linear separators). • Goal is for h to be close to c* over D. – err(h)=Prx 2 D(h(x) c*(x)) • Allow failure with small probability (to allow for chance that S is not representative). Maria-Florina Balcan

The Issue of Sample-Complexity • We want to do well on D, but all we have is S. – Are we in trouble? – How big does S have to be so that low error on S implies low error on D? • Luckily, sample-complexity bounds. • Algorithm: Pick a concept that agrees with S. • Sample Complexity Statement: – If |S| ¸ (1/ )[log|C| + log 1/ ], then with probability at least (1 ), all h 2 C that agree with sample S have true error · . Maria-Florina Balcan

Outline of the talk • Brief Overview of Supervised Learning – PAC Model • Semi-Supervised Learning – An Augmented PAC Style Model Maria-Florina Balcan

Combining Labeled and Unlabeled Data • Hot topic in recent years in Machine Learning. • Many applications have lots of unlabeled data, but labeled data is rare or expensive: • Web page, document classification • OCR, Image classification • Several methods have been developed to try to use unlabeled data to improve performance, e. g. : • Transductive SVM • Co-training • Graph-based methods Maria-Florina Balcan

An Augmented PAC style Model for Semi-Supervised Learning • Extends PAC naturally to the case of learning from both labeled and unlabeled data. • Unlabeled data is useful if we have beliefs not only about the form of the target, but also about its relationship with the underlying distribution. – Different algorithms are based on different assumptions about how data should behave. – Question – how to capture many of the assumptions typically used? Maria-Florina Balcan

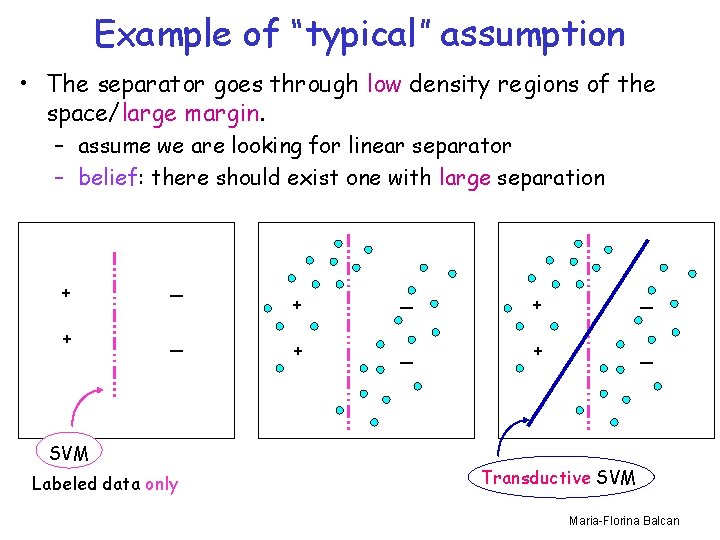
Example of “typical” assumption • The separator goes through low density regions of the space/large margin. – assume we are looking for linear separator – belief: there should exist one with large separation + _ SVM Labeled data only + _ + _ Transductive SVM Maria-Florina Balcan

Another Example • Agreement between two parts : co-training. – examples contain two sufficient sets of features • i. e. an example is x=h x 1, x 2 i – belief: the two parts of the example are consistent • 9 c 1, c 2 such that c 1(x 1)=c 2(x 2)=c*(x) – for example, if we want to classify web pages: Maria-Florina Balcan

Another Example, cont • Agreement between two parts : co-training. – examples contain two sufficient sets of features • i. e. an example is x=h x 1, x 2 i – belief: the two parts of the example are consistent • 9 c 1, c 2 such that c 1(x 1)=c 2(x 2)=c*(x) – for example, if we want to classify web pages: x = h x 1, x 2 i Prof. Avrim Blum My Advisor x - Link info & Text info Prof. Avrim Blum My Advisor x 1 - Link info x 2 - Text info Maria-Florina Balcan

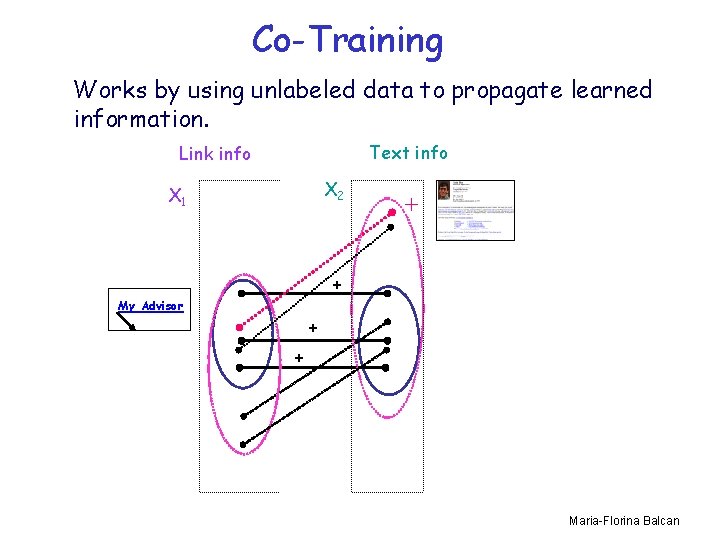
Co-Training Works by using unlabeled data to propagate learned information. Text info Link info X 2 X 1 + + My Advisor + + Maria-Florina Balcan

Semi-Supervised Learning Formalization. Main Idea • Augment the notion of a concept class C with a notion of compatibility between a concept and the data distribution ( (h, D) 2 [0, 1]). • “Learn C” becomes “learn (C, )” (i. e. learn class C under compatibility notion ). • Express relationships that one hopes the target function and underlying distribution will possess. Maria-Florina Balcan

Semi-Supervised Learning Formalization. Main Idea • Augment the notion of a concept class C with a notion of compatibility between a concept and the data distribution ( (h, D) 2 [0, 1]). • “Learn C” becomes “learn (C, )” (i. e. learn class C under compatibility notion ). • Express relationships that one hopes the target function and underlying distribution will possess. • Use unlabeled data & the belief that the target is compatible to reduce C down to just {the highly compatible functions in C}. Maria-Florina Balcan

Semi-Supervised Learning Formalization. Main Idea, cont • Use unlabeled data & our belief to reduce size(C) down to size(highly compatible functions in C) in our sample complexity bounds. • Need to analyze how much unlabeled data is needed to uniformly estimate compatibilities well. • Require that the degree of compatibility be something that can be estimated from a finite sample. Maria-Florina Balcan

Margins, Compatibility • Margins: belief is that there should exist a separator with margin . Highly compatible • + _ (h, D) =1 -(the probability mass within distance of h). • can be estimated from a finite sample. Maria-Florina Balcan

Types of Results in Our Model • As in the usual PAC model, can discuss algorithmic and sample complexity issues. • Can analyze how much unlabeled data we need to see: – depends both on the complexity of C and the complexity of our notion of compatibility. • Can analyze the ability of a finite unlabeled sample to reduce our dependence on labeled examples: – as a function of compatibility of the target function and various measures of the helpfulness of the distribution. Maria-Florina Balcan

Examples of Results in Our Model • Algorithm: pick a compatible concept that agrees with the labeled sample. • Sample Complexity Statement: Maria-Florina Balcan

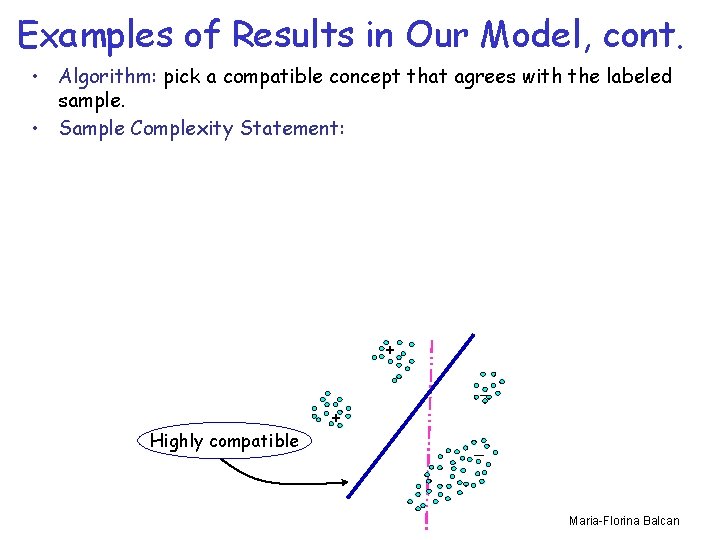
Examples of Results in Our Model, cont. • Algorithm: pick a compatible concept that agrees with the labeled sample. • Sample Complexity Statement: + _ Highly compatible + _ Maria-Florina Balcan

Summary • Provided a PAC style model for semi-supervised learning. • Captures many of the ways in which unlabeled data is typically used. • Unified framework for analyzing when and why unlabeled data can help. • Can get much better bounds in terms of labeled examples. Maria-Florina Balcan

Maria-Florina Balcan