A TBRbased Trajectory PiecewiseLinear Algorithm for Generating Accurate

A TBR-based Trajectory Piecewise-Linear Algorithm for Generating Accurate Low-order Models for Nonlinear Analog Circuits and MEMS Dmitry Vasilyev, Michał Rewieński, Jacob White Massachusetts Institute of Technology

Outline n Background n n Trajectory-piecewise linear (TPWL) framework for model order reduction Choice of projection bases n TBR-based reduction procedure for TPWL model reduction n Examples and computational results n Issues in selecting order of the model n Efficiency and accuracy n Future work and conclusions

Differential Equation Model n Original complex model: n Model can represent: Finite-difference spatial discretization of PDEs n Circuits with linear capacitors and inductors n Need accurate input-output behavior

Model reduction problem n n Original complex model: n Reduced model: Requirements for reduced model 3 n Want q << n (cost of simulation is q ) r n Want y (t) to be close to y(t)

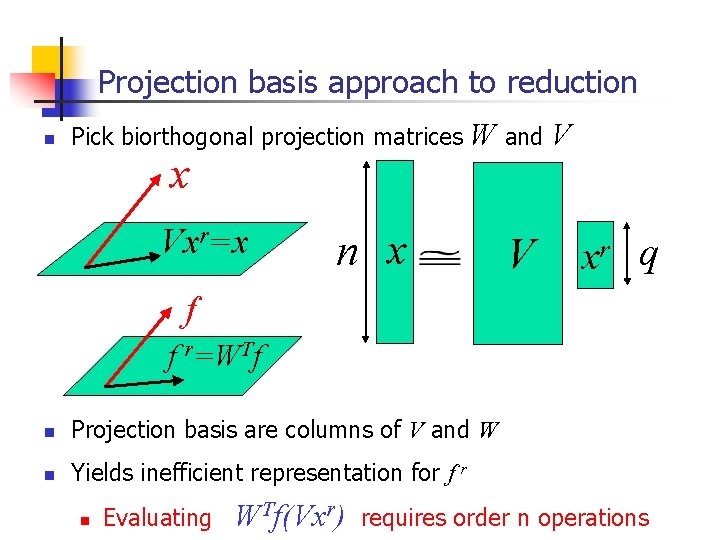
Projection basis approach to reduction n Pick biorthogonal projection matrices x Vxr=x W and V n x V xr q f f r=WTf n Projection basis are columns of V and W n Yields inefficient representation for f r n Evaluating WTf(Vxr) requires order n operations

Trajectory Piecewise Linear approximation of f( ) [Rewieński, 2001] Training trajectory x 0 x 1 x 2 … xn Simulating trajectory wi(x) is zero outside circle

Projection and TPWL approximation yields efficient f r( ) qx 1 WT Ai A ir V = n n A ir q q

TPWL approximation of f( ). Extraction algorithm x 0 Initial system position x 1 x 2 … xn Training trajectory Non-reduced state space 1. Compute A 1 2. Obtain W 1 and V 1 using linear reduction for A 1 3. Simulate training input, collect and reduce linearizations Air = W 1 TAi. V 1 f r (xi)=W 1 Tf(xi)

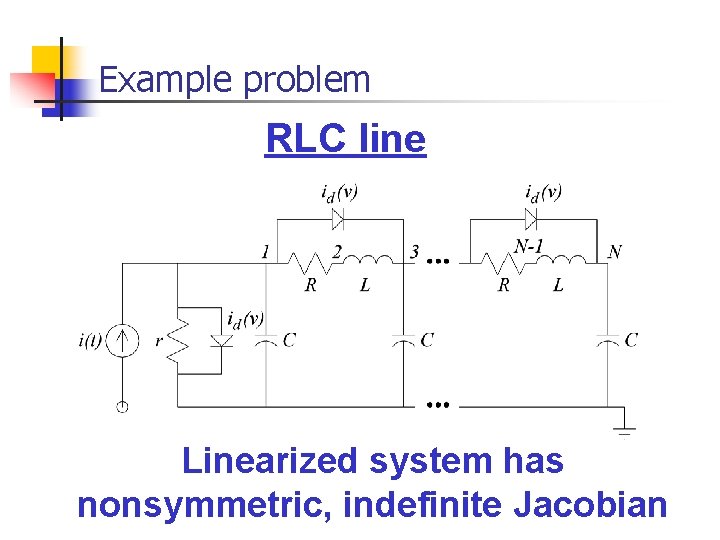
Example problem RLC line Linearized system has nonsymmetric, indefinite Jacobian

Numerical results – nonlinear RLC transmission line System response for input current i(t) = (sin(2π/10)+1)/2 Input: training input testing input Voltage at node 1 [V] n Time [s]

Outline n Background n n Trajectory-piecewise linear (TPWL) framework for model order reduction Choice of projection bases n TBR-based reduction procedure for TPWL model reduction n Examples and computational results n Issues in selecting order of the model n Efficiency and accuracy n Future work and conclusions

Key issue: choosing projection basis Krylov-subspace methods n Fast n Don’t guarantee accuracy Balanced-truncation methods n Expensive (~n 3) n Guarantee accuracy

Key issue: choosing projection Krylov-subspace methods Balanced-truncation methods Result: projection matrices W and V

The matter of this presentation Which method more suitable for TPWL? Krylov-subspace methods Balanced-truncation methods Can we use it? Used in previous works Our presentation aims to answer this question

Reminder: TBR reduction algorithm Given linear system (A, B, C) 1)Compute Controllability and observability gramians P and Q 2)Compute Cholesky factor of P: P = RTR 3)Compute SVD of RQRT: UΣ 2 UT = RQRT Diagonal values of Σ are called the Hankel singular values 4)Projection basis V contains first r columns of the balancing transformation T = RTU Σ-1/2

Our Approach: x 0 n Use TPWL to handle nonlinearity x 1 x 2 … xn n Use TBR for projection matrices W and V

Outline n Background n n Trajectory-piecewise linear (TPWL) framework for model order reduction Choice of projection bases n TBR-based reduction procedure for TPWL model reduction n Examples and computational results n Issues in selecting order of the model n Efficiency and accuracy n Future work and conclusions

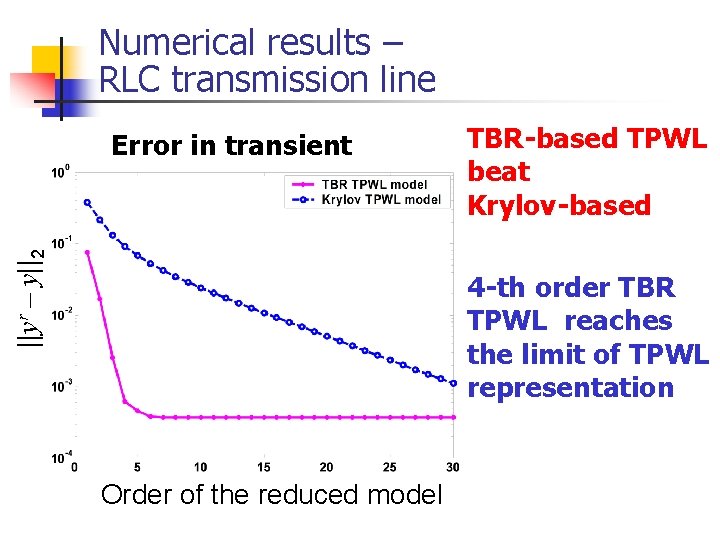
Numerical results – RLC transmission line ||yr – y||2 Error in transient TBR-based TPWL beat Krylov-based 4 -th order TBR TPWL reaches the limit of TPWL representation Order of the reduced model

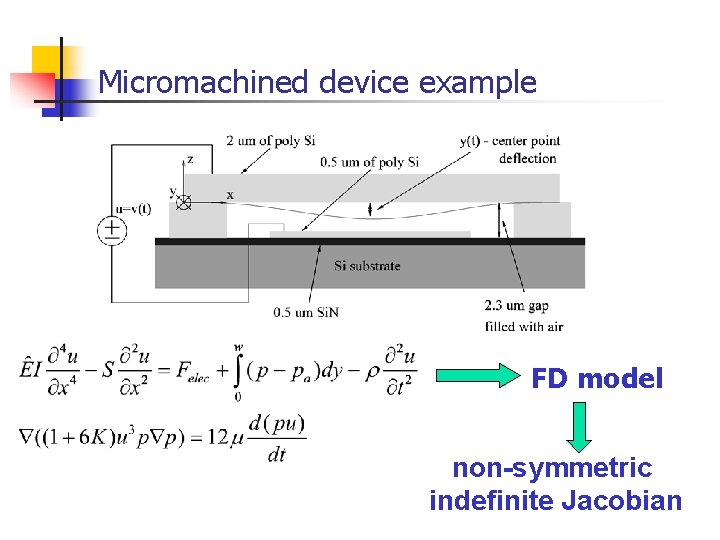
Micromachined device example FD model non-symmetric indefinite Jacobian

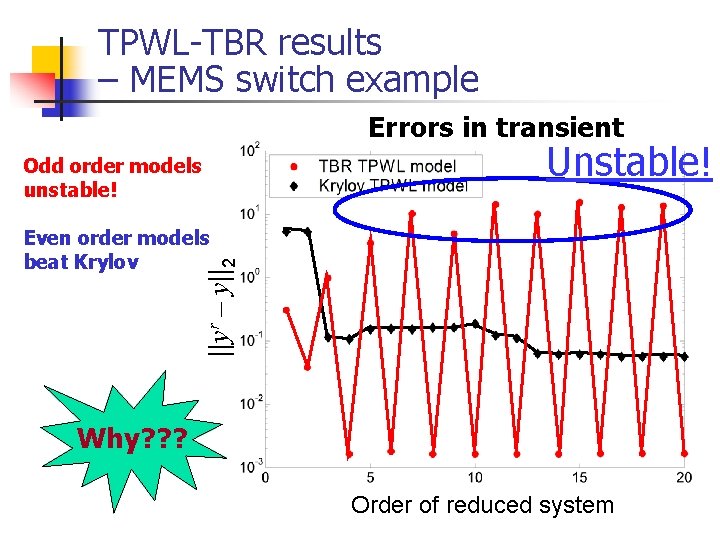
TPWL-TBR results – MEMS switch example Errors in transient Unstable! Odd order models unstable! ||yr – y||2 Even order models beat Krylov Why? ? ? Order of reduced system

Outline n Background n n Trajectory-piecewise linear (TPWL) framework for model order reduction Choice of projection bases n TBR-based reduction procedure for TPWL model reduction n Examples and computational results n Issues in selecting order of the model n Efficiency and accuracy n Future work and conclusions

Illustrating even-odd behavior for MEMS beam example Observation: First-point Jacobian has many complex-conjugate eigenvalues. Just curious: How complex-conjugate pairs are represented by TPWL models?

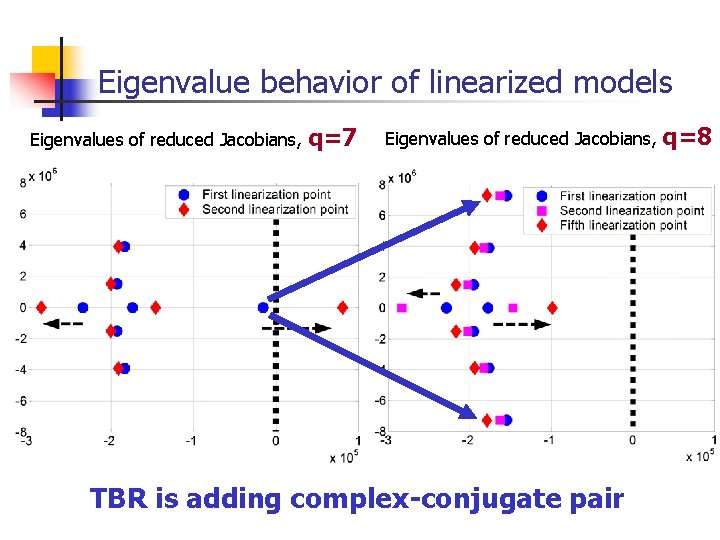
Eigenvalue behavior of linearized models Eigenvalues of reduced Jacobians, q=7 Eigenvalues of reduced Jacobians, TBR is adding complex-conjugate pair q=8

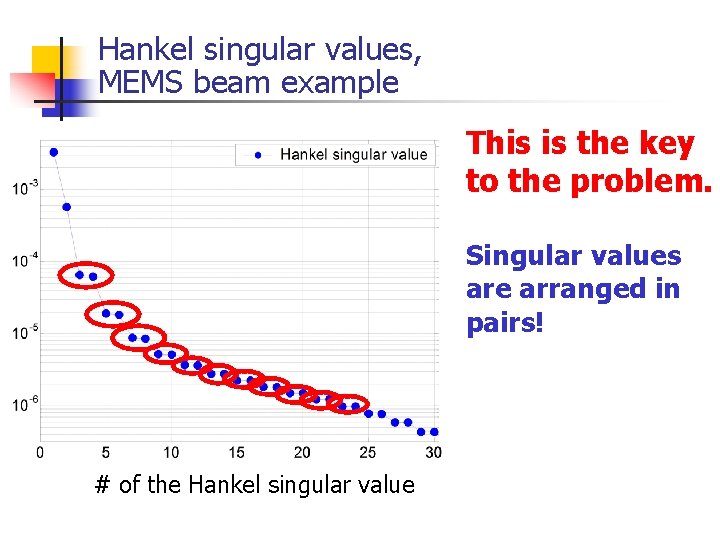
Hankel singular values, MEMS beam example This is the key to the problem. Singular values are arranged in pairs! # of the Hankel singular value

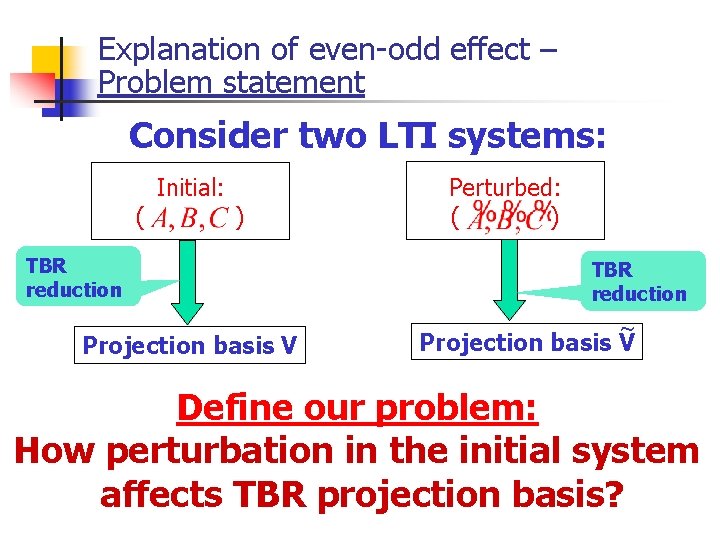
Explanation of even-odd effect – Problem statement Consider two LTI systems: ( Initial: ) TBR reduction Projection basis V Perturbed: ( ) TBR reduction ~ Projection basis V Define our problem: How perturbation in the initial system affects TBR projection basis?

TBR reduction algorithm 1) Compute Controllability and observability gramians P and Q 2) Compute Cholesky factor of P: P = RTR 3) Compute SVD of RQRT: UΣ 2 UT = RQRT 4) Projection basis V is first r columns of the matrix T = RTU Σ-1/2 Our goal: How perturbation in the initial system affects balancing transformation T ?

TBR reduction algorithm Perturbation behavior of TBR projection is dictated by: 3) Compute SVD of RQRT: UΣ 2 UT = RQRT Symmetric eigenvalue problem for RQRT

Perturbation theory for symmetric eigenvalue problem Eigenvectors of M 0 : Eigenvectors of M 0 + Δ : Mixing of eigenvectors (assuming small perturbations): cik large when λi 0 ≈ λk 0

Explaining even-odd behavior The closer Hankel singular values lie to each other, the more corresponding eigenvectors of V tend to intermix! n Analysis implies simple recipe for using TBR n n Pick reduced order to insure n Remaining Hankel singular values are small enough n The last kept and first removed Hankel Singular Values are well separated Helps insure that all linearizations stably reduced

Outline n Background n n Trajectory-piecewise linear (TPWL) framework for model order reduction Choice of projection bases n TBR-based reduction procedure for TPWL model reduction n Examples and computational results n Issues in selecting order of the model n Efficiency and accuracy n Future work and conclusions

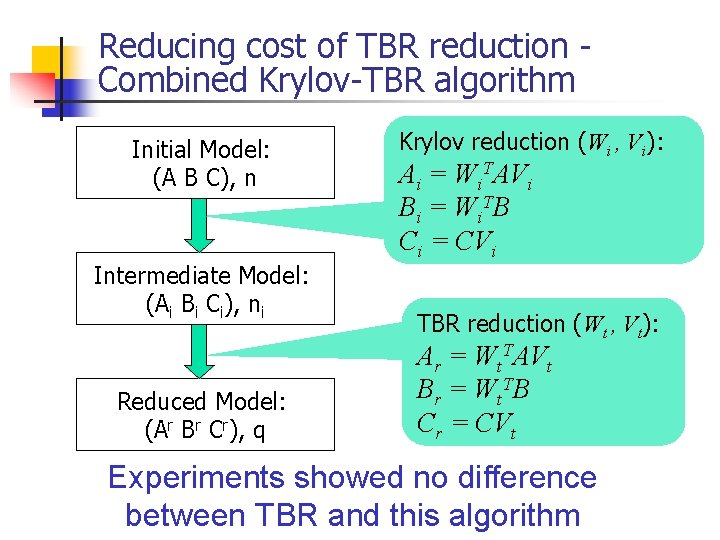
Reducing cost of TBR reduction Combined Krylov-TBR algorithm Initial Model: (A B C), n Intermediate Model: (Ai Bi Ci), ni Reduced Model: (Ar Br Cr), q Krylov reduction (Wi , Vi): Ai = Wi. TAVi B i = Wi T B Ci = CVi TBR reduction (Wt , Vt): Ar = Wt. TAVt B r = Wt T B Cr = CVt Experiments showed no difference between TBR and this algorithm

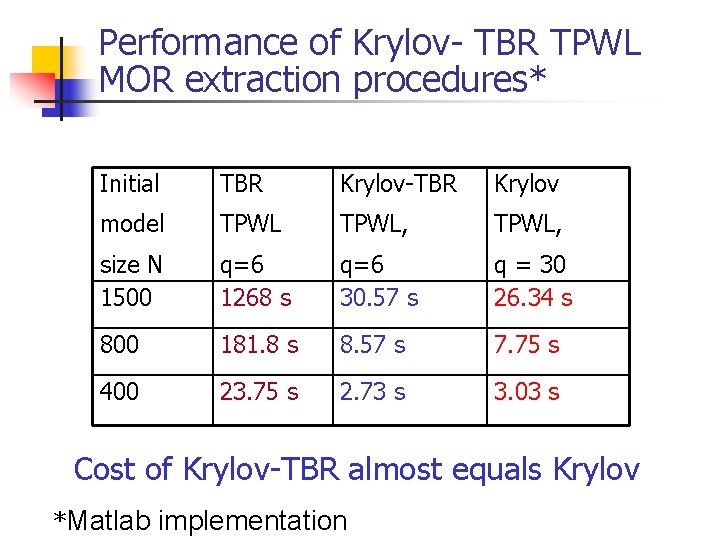
Performance of Krylov- TBR TPWL MOR extraction procedures* Initial TBR Krylov-TBR Krylov model TPWL, size N 1500 q=6 1268 s q=6 30. 57 s q = 30 26. 34 s 800 181. 8 s 8. 57 s 7. 75 s 400 23. 75 s 2. 73 s 3. 03 s Cost of Krylov-TBR almost equals Krylov *Matlab implementation

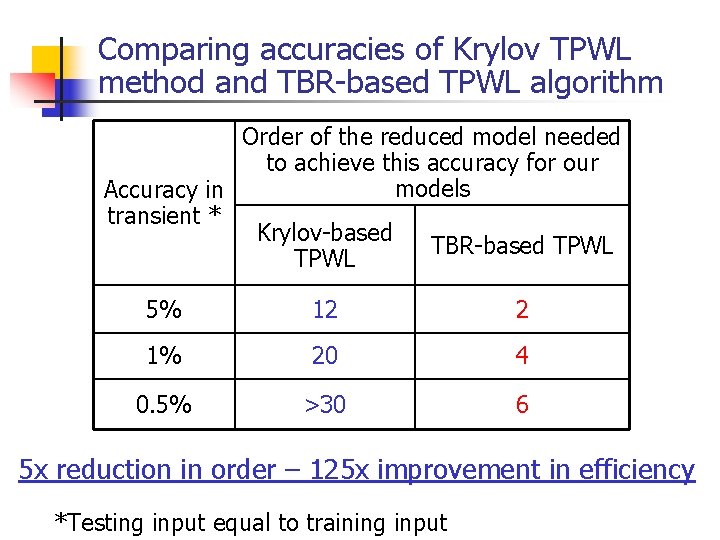
Comparing accuracies of Krylov TPWL method and TBR-based TPWL algorithm Order of the reduced model needed to achieve this accuracy for our models Accuracy in transient * Krylov-based TBR-based TPWL 5% 12 2 1% 20 4 0. 5% >30 6 5 x reduction in order – 125 x improvement in efficiency *Testing input equal to training input

Proposed improvement To aggregate projection bases: W 1 , V 1 W 2 , V 2 Biorthogonalization W 1 TV 1 = Ik 1 × k 1 W 2 TV 2 = Ik 2 × k 2 make Wagg , Vagg Wagg. TVagg = IN_agg × N_agg Nagg ≤ k 1 + k 2 Question. How to remove redundant directions? (in case of Krylov reduction we used SVD, since Krylov uses orthogonal projection)

Future work n n Are TBR-based TPWL models valid for unstable linearizations? What about systems having the following form (i. e. circuits with nonlinear capacitors):

Conclusions n n In this work we used TBR-based linear reduction procedure to generate TPWL reduced models Order reduced 5 times while maintaining comparable accuracy with Krylov TPWL method (efficiency improved 125 times!) Combined Krylov-TBR reduction allows to extract TPWL models at low cost One should take care of repeated or almost equal Hankel singular values when applying this method.