A talajok mechanikai tulajdonsgai V Korszer mechanikai modellek

A talajok mechanikai tulajdonságai V.

Korszerű mechanikai modellek

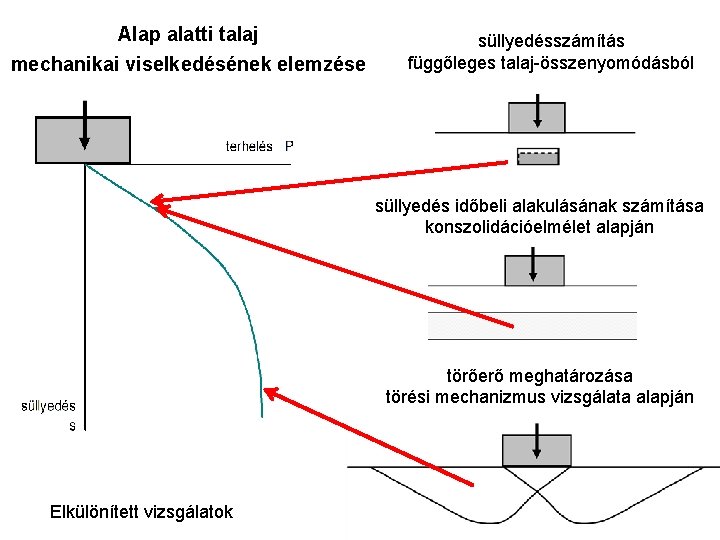
Alap alatti talaj mechanikai viselkedésének elemzése süllyedésszámítás függőleges talaj-összenyomódásból süllyedés időbeli alakulásának számítása konszolidációelmélet alapján törőerő meghatározása törési mechanizmus vizsgálata alapján Elkülönített vizsgálatok

A talajok mechanikai viselkedésének hagyományos kezelése egy alap alatti talaj példáján 1. alapok alatti feszültségszétterjedés számítása a lineáris rugalmasságtan alapján, azt feltételezve, hogy a talaj viselkedése egy bizonyos feszültségszintig rugalmas, 2. a talajdeformációk meghatározása lineáris feszültségalakváltozás összefüggéssel e „rugalmas” tartományra ésszerűen megválasztott modulusokkal, 3. az alakváltozások időbeli alakulásának elkülönített számítása lineáris konszolidációs modellel csak a kritikus talajzónákra 4. a képlékeny (törési) határállapot elkülönített vizsgálata a Coulomb-féle törési feltétel alkalmazásával törési mechanizmusokat feltételezve

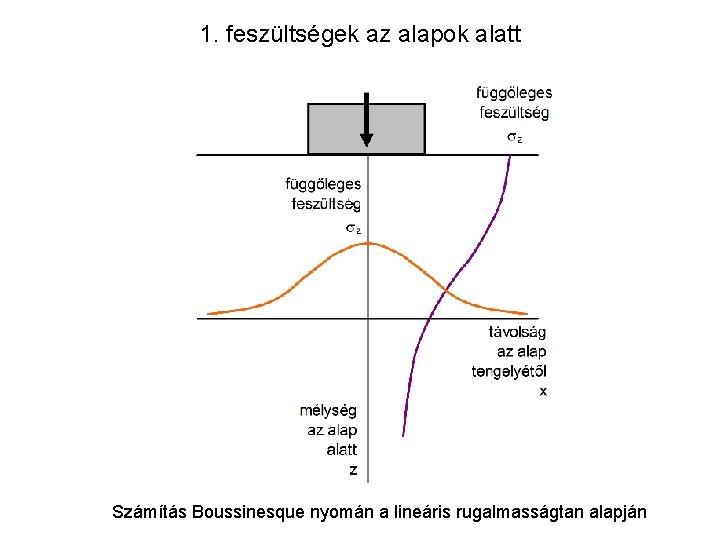
1. feszültségek az alapok alatt Számítás Boussinesque nyomán a lineáris rugalmasságtan alapján

2. Alakváltozások számítása lineáris feszültség-alakváltozás kapcsolattal Térbeli feszültségi-alakváltozási állapot Lineáris alakváltozási állapot

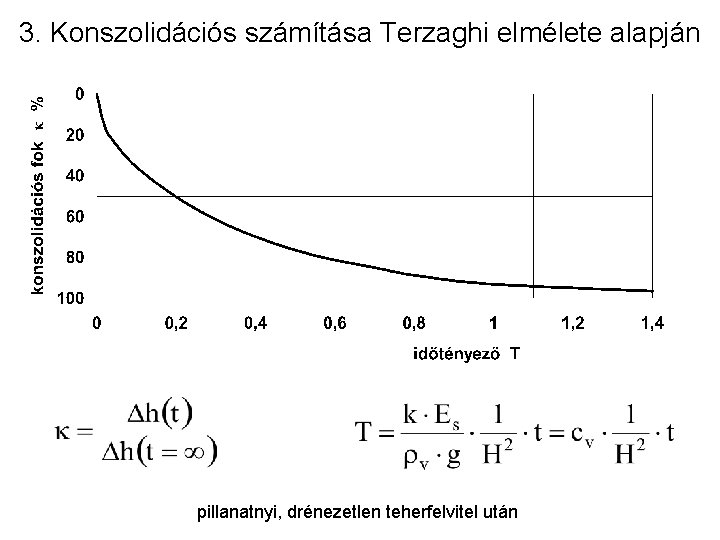
3. Konszolidációs számítása Terzaghi elmélete alapján pillanatnyi, drénezetlen teherfelvitel után

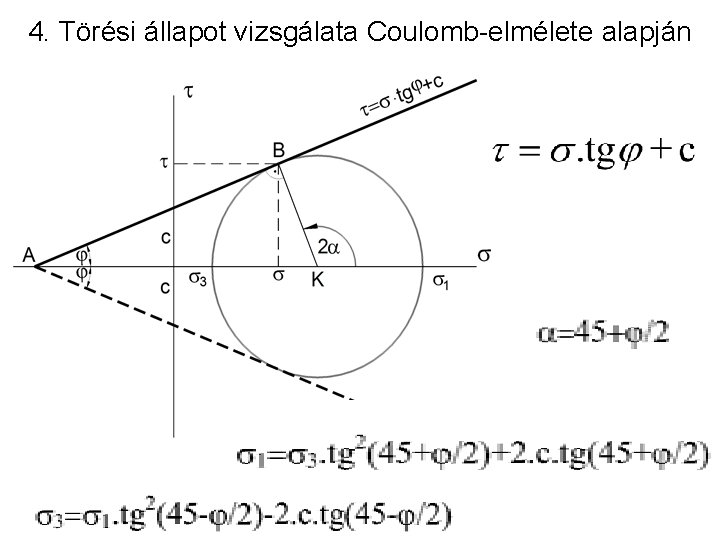
4. Törési állapot vizsgálata Coulomb-elmélete alapján

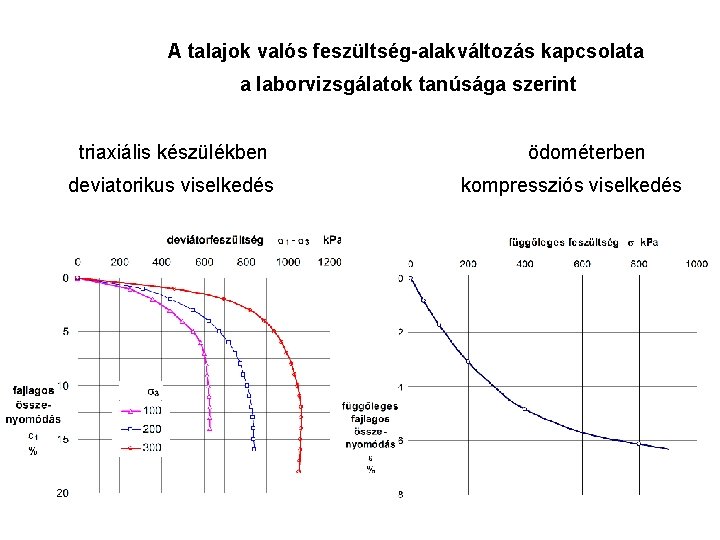
A talajok valós feszültség-alakváltozás kapcsolata a laborvizsgálatok tanúsága szerint triaxiális készülékben deviatorikus viselkedés ödométerben kompressziós viselkedés

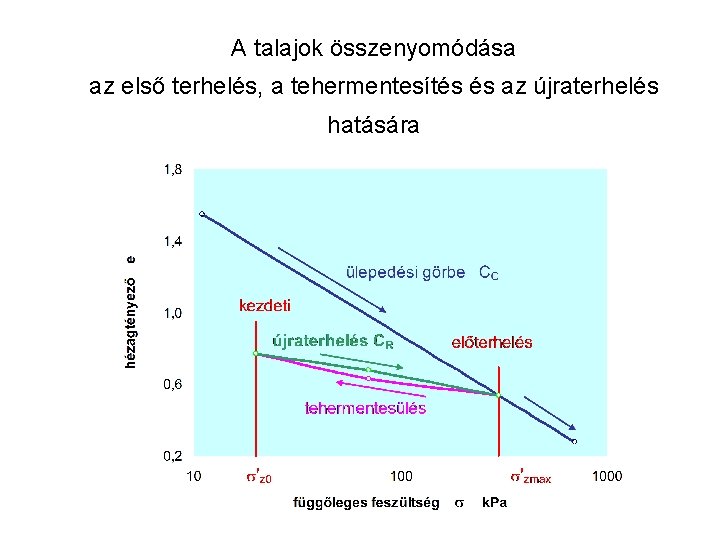
A talajok összenyomódása az első terhelés, a tehermentesítés és az újraterhelés hatására

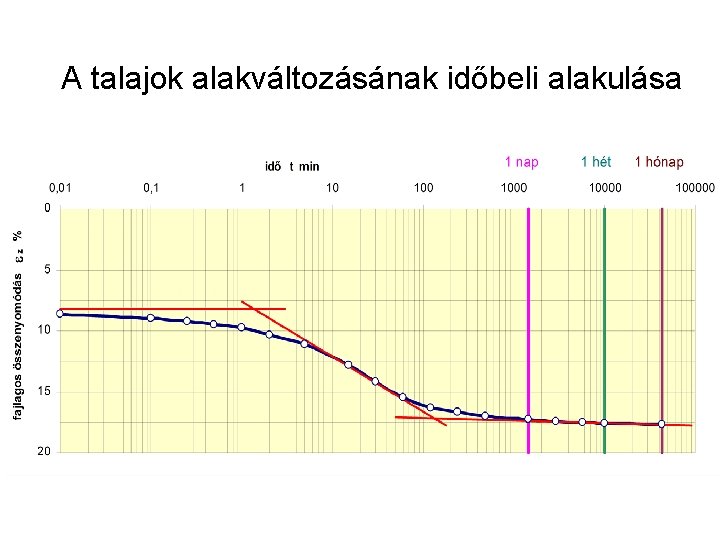
A talajok alakváltozásának időbeli alakulása

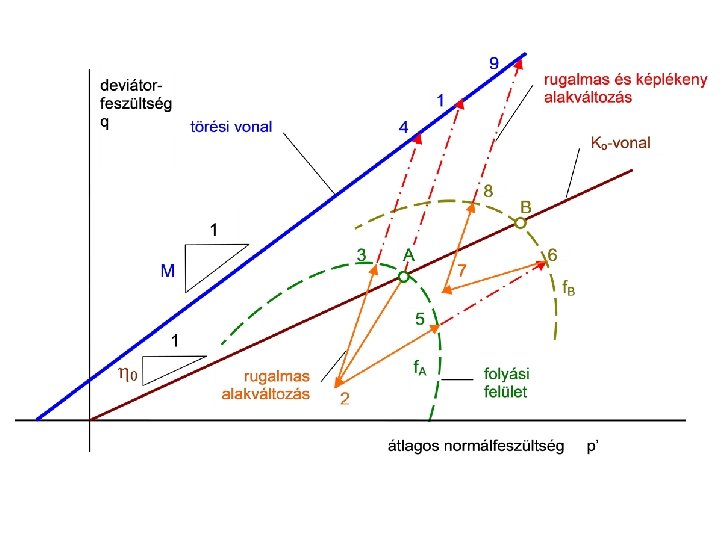
Eltérések az idealizált viselkedésétől • homogén? előterheltséggel, mélységgel javul • izotróp? vízszintesen más, mint függőlegesen • rugalmas? • lineáris? tehermentesülés és újraterhelés közben szűk feszültségtartományokban • képlékeny? az első terhelés hatására a kezdetektől • tönkremenetel? deviátorfeszültség hatására • javulás? az átlagos normálfeszültség hatására • konszolidáció? a tehernövekedés alatt is

x 1 y 2 z 3 xy yz zx a b d Feszültségjellemzők

ex ey ez gxy gyz gzx e 1 e 2 e 3 a b d Alakváltozási jellemzők

Izotróp, homogén, lineárisan rugalmas anyag Hooke-törvény általánosított felírása

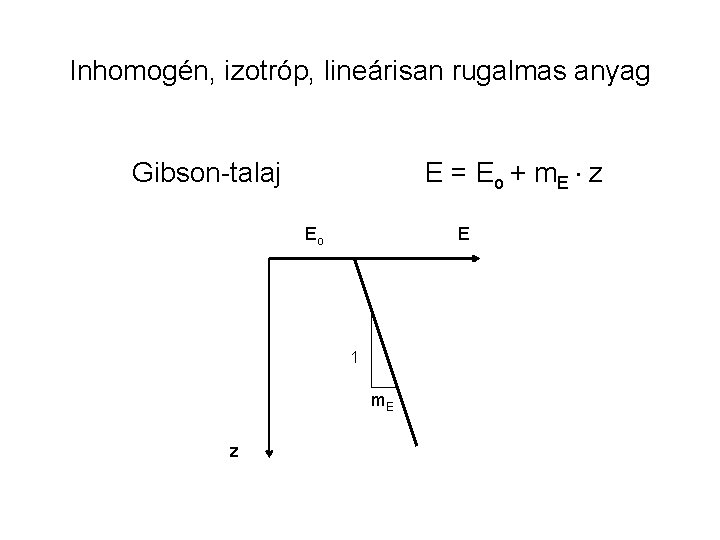
Inhomogén, izotróp, lineárisan rugalmas anyag E = E o + m. E z Gibson-talaj Eo E 1 m. E z

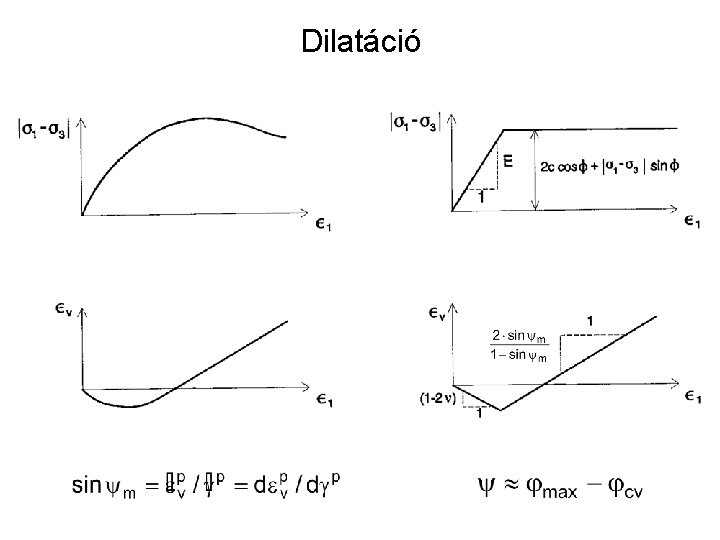
Dilatáció

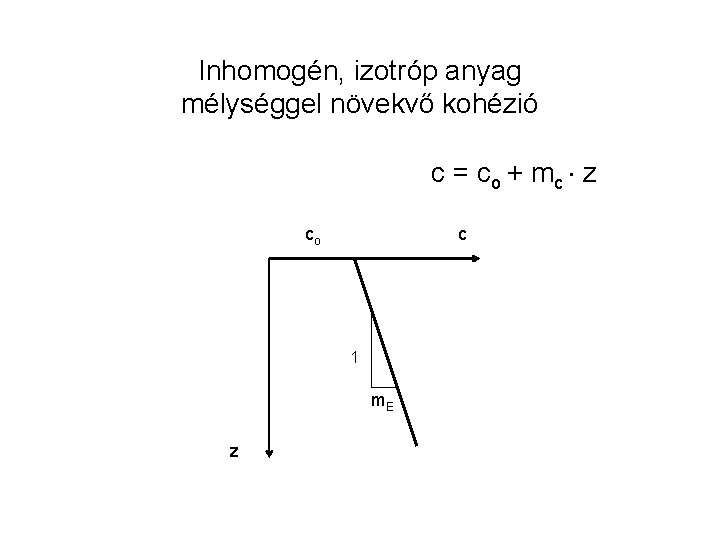
Inhomogén, izotróp anyag mélységgel növekvő kohézió c = co + m c z co c 1 m. E z

Homogén, keresztirányban anizotróp, lineárisan rugalmas anyag Feszültség alakváltozási összefüggések (fizikai egyenletek) Független anyagjellemzők Anyagjellemzők kapcsolata

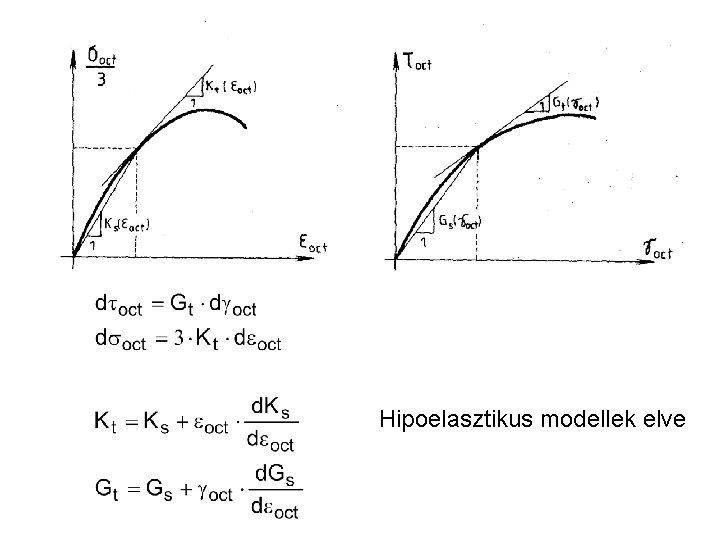
Hipoelasztikus modellek elve

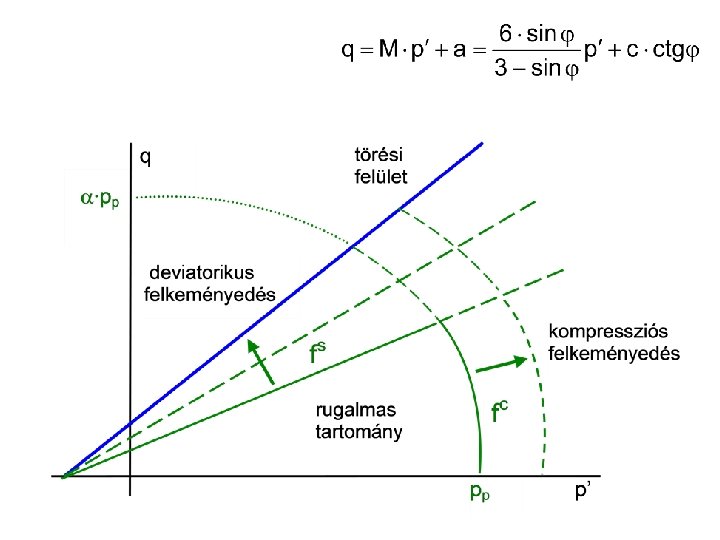
Felkeményedő talaj: deviatorikus viselkedés E 50 ≈ Eoed Eur ≈ (3… 5)∙E 50

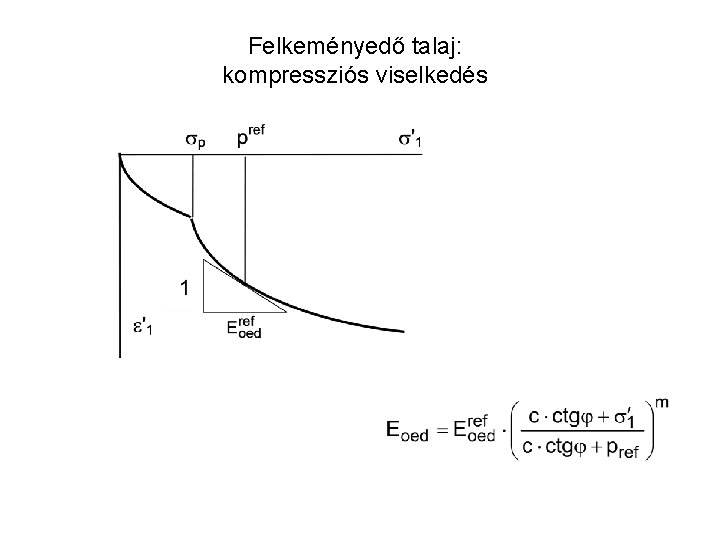
Felkeményedő talaj: kompressziós viselkedés

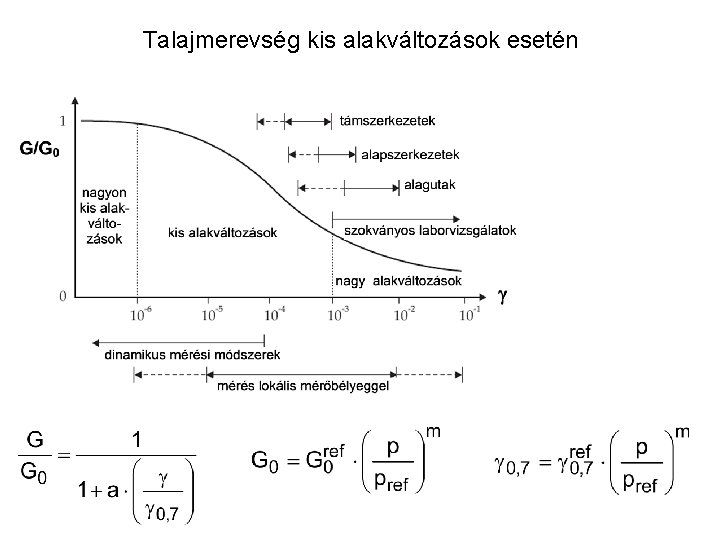
Talajmerevség kis alakváltozások esetén