A STOCHASTIC VARIATIONAL MULTISCALE METHOD WITH EXPLICIT SUBGRID

A STOCHASTIC VARIATIONAL MULTISCALE METHOD WITH EXPLICIT SUBGRID MODELING FOR ADVECTIONDIFFUSION SYSTEMS NICHOLAS ZABARAS and B. VELAMUR ASOKAN Materials Process Design and Control Laboratory Sibley School of Mechanical and Aerospace Engineering 169 Frank H. T. Rhodes Hall Cornell University Ithaca, NY 14853 -3801 Email: zabaras@cornell. edu, bnv 2@cornell. edu URL: http: //mpdc. mae. cornell. edu/ Materials Process Design and Control Laboratory

OUTLINE q Stochastic variational multiscale method q Uncertainty modeling – Overview and techniques q Stochastic advection-diffusion systems – ASGS modeling q Stochastic fluid-flow – ASGS modeling q Stochastic natural-convection – capturing unstable equilibrium q Stochastic multiscale elliptic equation q Stochastic multiscale advection-diffusion q Extensions and future research Materials Process Design and Control Laboratory

MULTISCALE TRANSPORT SYSTEMS Solidification Fluid-flow Diffusion in composites q Presence of various spatial and temporal length scales q Varied application areas – Engineering, Material science and other q Uncertainty manifests from impreciseness in boundary condition, material property specification and other modeling assumptions Materials Process Design and Control Laboratory

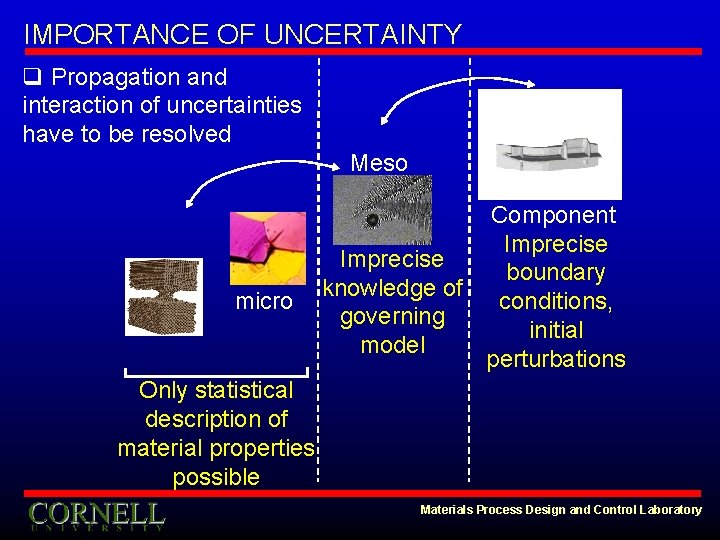
IMPORTANCE OF UNCERTAINTY q Propagation and interaction of uncertainties have to be resolved Meso micro Component Imprecise boundary knowledge of conditions, governing initial model perturbations Only statistical description of material properties possible Materials Process Design and Control Laboratory

MODELING ASPECTS OF UNCERTAINTY q Probabilistic interpretation – Imprecise knowledge about boundary conditions, governing models, material properties described using stochastic processes q Uncertainty due to codes, algorithms, machine precision are not considered here q Physically, the uncertainty at progressively finer scales is higher [fluctuations] q Ideally, our computation paradigm should reflect above consideration q Computational approach should be orders of magnitude faster than other uncertainty analysis approaches that are sampling based Materials Process Design and Control Laboratory

q Uncertainty representation techniques q Introduction to spectral stochastic theory [Ghanem, Stochastic finite elements: A spectral approach] q Generalized polynomial chaos expansion [Karniadakis, J. Fluids Engrg. , 125, 2001] q Support-space [stochastic Galerkin expansion] [Zabaras, JCP, 208, 2005], [Babuska SIAM J. Num. Anal. , 42, 2005] Materials Process Design and Control Laboratory

STOCHASTIC PROCESSES AS FUNCTIONS q A probability space is a triple comprising of collection of the sample space , the s-algebra of subsets (events) of and the probability measure on. q A real-valued random variable is a function that maps the probability space to a real line [regions in go to intervals in the real line] q : Random variable q A space-time stochastic process is can be represented as + other regularity conditions Materials Process Design and Control Laboratory

SERIES REPRESENTATION q For special kinds of stochastic processes that have finite variance-covariance function, we have mean-square convergent expansions Series expansions q Known covariance function q Unknown covariance function Karhunen-Loeve Generalized polynomial chaos q Best approximation in mean-square sense q Can yield exponentially convergent expansions q Useful typically for input uncertainty modeling q Used typically for output uncertainty modeling Materials Process Design and Control Laboratory

SERIES REPRESENTATION [CONTD] q Karhunen-Loeve ON random variables Mean Stochastic Deterministic functions process function q The deterministic functions are based on the eigen-values and eigenvectors of the covariance function of the stochastic process. q The orthonormal random variables depend on the kind of probability distribution attributed to the stochastic process. q Any function of the stochastic process (typically the solution of PDE system with as input) is of the form Materials Process Design and Control Laboratory

SERIES REPRESENTATION [CONTD] q Generalized polynomial chaos expansion is used to represent quantities like Stochastic input Askey polynomials in input Deterministic functions Stochastic process q The Askey polynomials depend on the kind of joint PDF of the orthonormal random variables q Typically: Gaussian – Hermite, Uniform – Legendre, Beta -Jacobi polynomials Materials Process Design and Control Laboratory

NEED FOR SUPPORT-SPACE APPROACH q GPCE and Karhunen-Loeve are Fourier like expansions q Gibb’s effect in describing highly nonlinear, discontinuous uncertainty propagation Onset of natural convection [Zabaras JCP 208(1)] – Using support-space method [Ghanem JCP 197(1)] – Using Wiener-Haar wavelets q Finite element representation of stochastic processes [stochastic Galerkin method: Babuska et al] q Incorporation of importance based meshing concept for improving accuracy [support space method] Materials Process Design and Control Laboratory

SUPPORT-SPACE [STOCHASTIC GALERKIN] q Let stochastic inputs be represented by ON random variables with a joint PDF q Support space is the region in the span of stochastic input that has a positive PDF q Example of a 2 D input and associated support-space PDF Grid q Piecewise polynomials defined on support-space grid Materials Process Design and Control Laboratory

q VMS – Basic idea q Algebraic subgrid modeling approaches q Illustration of the approach with derivation of subgrid problems for stochastic natural convection equation q Numerical examples q Stochastic advection-diffusion equation q Stochastic fluid-flow q Stochastic natural convection [GPCE approach and capturing unstable equilibrium using support-space method] Materials Process Design and Control Laboratory

VMS – ILLUSTRATION [NATURAL CONVECTION] Continuity Momentum Energy Constitutive laws Materials Process Design and Control Laboratory

DEFINITION OF FUNCTION SPACES q Deterministic function spaces q Stochastic function spaces – The space of all second order random variables is critical to spectral uncertainty modeling Materials Process Design and Control Laboratory

DERIVED FUNCTION SPACES q Velocity function space q Test q Trial q Pressure function space q Test q Trial q Energy function space q Test q Trial Materials Process Design and Control Laboratory

VARIATIONAL FORMULATION q Energy equation – Find following holds such that, for all , the q Momentum and continuity equation – Find such that, for all , the following holds q Wherein, and are the random Rayleigh number and Prandtl number, respectively. These will be defined separately for each example considered. Materials Process Design and Control Laboratory

VMS HYPTOTHESIS q VMS hypothesis: Exact solution can be written as a sum of coarse scale resolved components [bar quantities] and subgrid scale unresolved components [prime quantities] q Induced function space decomposition [Hughes 1995]: This induces a function space decomposition as follows q The coarse scale function spaces are to be approximated using finite element basis functions, the small scales are to be solved using Green’s functions, element Fourier transform and other Materials Process Design and Control Laboratory

q Stochastic VMS applied to the energy equation – The algebraic subgrid modeling approach q Scale decomposed variational formulation q Element Fourier transform [Codina, CMAME 191, 2002] q Algebraic subgrid scale model [Stochastic] q Modified coarse scale equation Materials Process Design and Control Laboratory

ENERGY EQUATION – SCALE DECOMPOSITION q Energy equation – Find and , the following holds such that, for all q Coarse scale variational formulation q Subgrid scale variational formulation q These equations can be re-written in the strong form with assumption on regularity as follows Materials Process Design and Control Laboratory

ASGS APPROACHES q In VMS, the central idea is to solve the subgrid scale variational formulation in an approximate manner q Different techniques to generate an algebraic subgrid scale model [approximation] are q Green’s functions and Residual-free bubbles q Element Fourier transform q Two-level finite element methods q Spatial domain discretized into Nel disjoint finite element sub-domains Spatial domain discretized Materials Process Design and Control Laboratory

ELEMENT FOURIER TRANSFORM q For a random field defined over a coarse element subdomain, the element Fourier transform is defined as q The spatial derivative can now be represented as Term is negligible for large wave numbers Note – Subgrid solution denotes fluctuations and hence is captured with large wave number terms Materials Process Design and Control Laboratory

ASGS MODEL FOR ENERGY EQUATION Time integration rule Time-discretized equation After application of Parseval’s and Mean value theorem Materials Process Design and Control Laboratory

MODIFIED COARSE FORMULATION q We assume the following strong regularity conditions q Applying the ASGS model, we obtain the following modified coarse scale equation q. Time integration choice plays a role in deciding the coarse scale formulation Materials Process Design and Control Laboratory

VARIATIONAL MULTISCALE METHOD q The nonlinear advection term is linearized using Picard assumption [accurate for moderate Reynolds numbers] q Similar to the energy equation, we can derive the subgrid scale strong form of equations as follows Materials Process Design and Control Laboratory

ALGEBRAIC SUBGRID SCALE MODEL q After time discretization, application of element Fourier transform, we have q Application of mean value theorem and Parseval’s theorem Materials Process Design and Control Laboratory

MODIFIED COARSE FORMULATION q Assuming strong regularity conditions, we have q Modified coarse scale momentum equation Materials Process Design and Control Laboratory

MODIFIED COARSE FORMULATION q Modified coarse scale continuity equation q Wherein, the test function Materials Process Design and Control Laboratory

IMPLEMENTATION ISSUE - GPCE q Assume that the input can be represented as a function of orthonormal random variables Spatial random field Random variables Galerkin shape function q The random variables are represented in a GPCE Askey chaos polynomials GPCE coefficients Materials Process Design and Control Laboratory

IMPLEMENTATION ISSUES – SUPPORT-SPACE q We use a two level grid approach q Again, we assume that the input can be represented as a function of orthonormal polynomials Each Gauss point has an underlying support-space grid q Finite element interpolation at spatial and support-space grid q Object oriented structure: every coarse element has nbf basis functions, support-space grid has nbf’ basis functions Materials Process Design and Control Laboratory

CURSE OF DIMENSIONALITY q Both GPCE and support-space method are fraught with the curse of dimensionality q As the number of random input orthonormal variables increase, computation time increases exponentially q Support-space grid is usually in a higher-dimensional manifold (if the number of inputs is > 3), we need special tensor product techniques for generation of the support-space q Parallel implementations are currently performed using PETSc (Parallel scientific extensible toolkit ) Materials Process Design and Control Laboratory

q Numerical examples q Stochastic fluid flow – GPCE implementation q Stochastic natural convection – capturing unstable equilibrium using support-space methodology Materials Process Design and Control Laboratory

TRANSIENT ROTATING CONE PROBLEM q Advection velocity – pure rotation about origin q Fourth order Legendre chaos used for simulation q 1200 bilinear elements used for solution, preconditioned GMRES q Time of simulation [0, 9], time step [0. 003] q Transient response is observed Materials Process Design and Control Laboratory

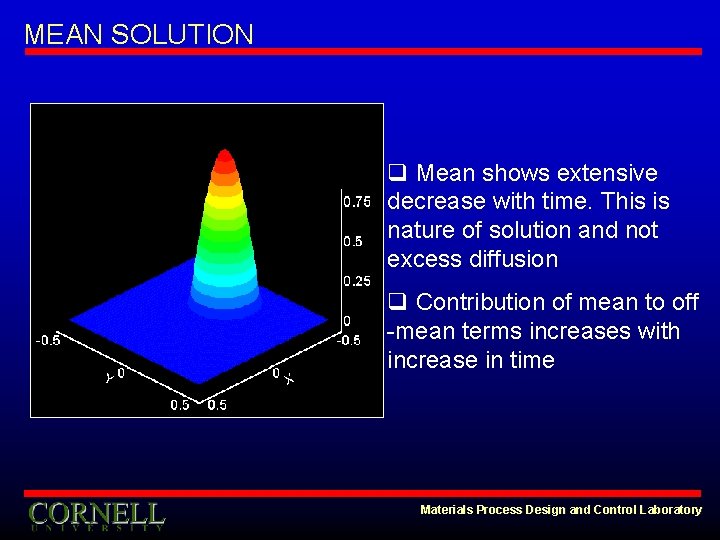
MEAN SOLUTION q Mean shows extensive decrease with time. This is nature of solution and not excess diffusion q Contribution of mean to off -mean terms increases with increase in time Materials Process Design and Control Laboratory

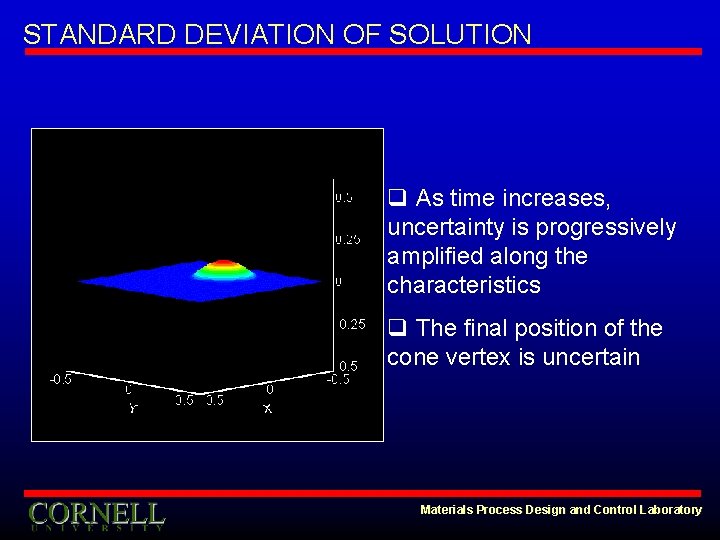
STANDARD DEVIATION OF SOLUTION q As time increases, uncertainty is progressively amplified along the characteristics q The final position of the cone vertex is uncertain Materials Process Design and Control Laboratory

FLOW PAST A CIRCULAR CYLINDER Traction free Uinlet = unif[-0. 9, 1. 1] q 2000 bilinear elements, 3 rd order Legendre chaos expansion for velocity and pressure, preconditioned GMRES No-slip q Time [0, 180], time step [0. 03], Kinematic viscosity [0. 01] q Onset of vortex shedding, wake characteristic Materials Process Design and Control Laboratory

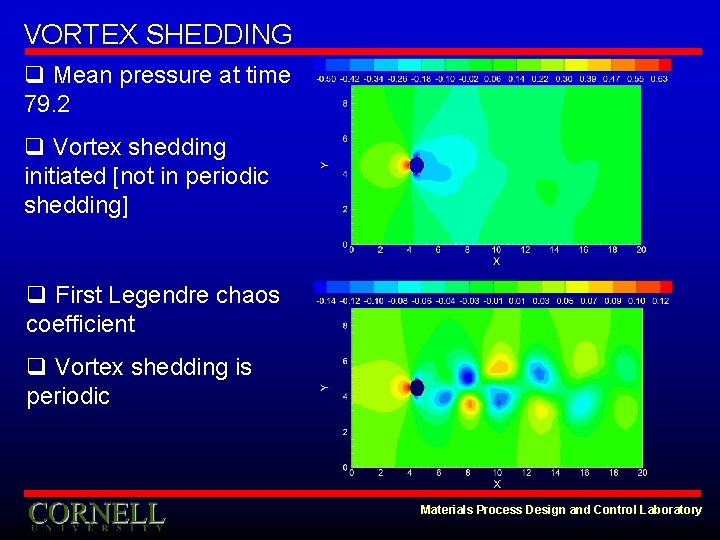
VORTEX SHEDDING q Mean pressure at time 79. 2 q Vortex shedding initiated [not in periodic shedding] q First Legendre chaos coefficient q Vortex shedding is periodic Materials Process Design and Control Laboratory

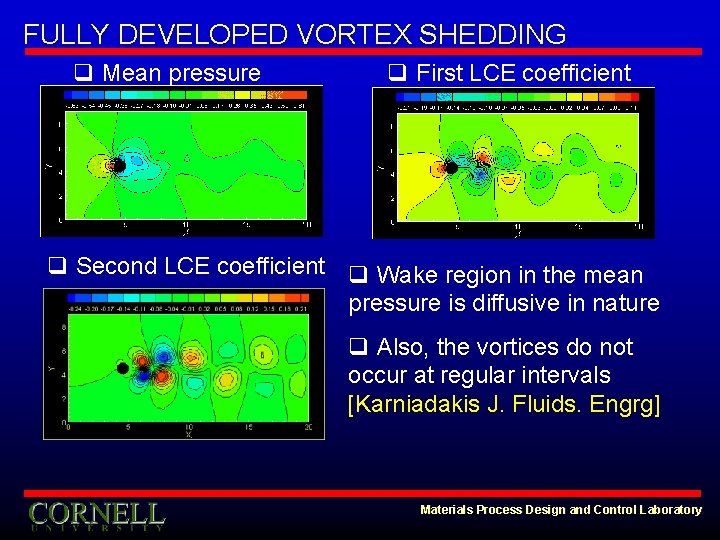
FULLY DEVELOPED VORTEX SHEDDING q Mean pressure q First LCE coefficient q Second LCE coefficient q Wake region in the mean pressure is diffusive in nature q Also, the vortices do not occur at regular intervals [Karniadakis J. Fluids. Engrg] Materials Process Design and Control Laboratory

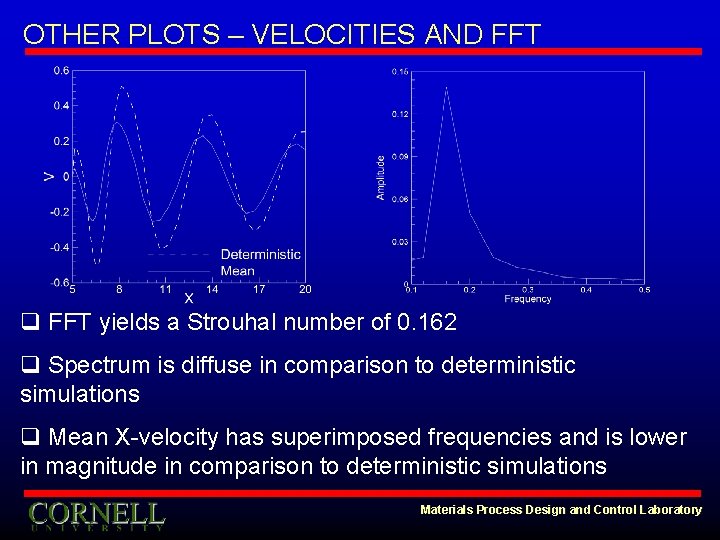
OTHER PLOTS – VELOCITIES AND FFT q FFT yields a Strouhal number of 0. 162 q Spectrum is diffuse in comparison to deterministic simulations q Mean X-velocity has superimposed frequencies and is lower in magnitude in comparison to deterministic simulations Materials Process Design and Control Laboratory

NATURAL CONVECTION – GPCE q 2048 bilinear elements, 3 rd order Legendre chaos expansion for velocity and pressure, preconditioned GMRES q Time [0, 1. 5] Cold wall q = 0 Insulated q Time step [0. 002] q Rayleigh number [104] q Prandtl number [0. 7] q Transient behavior response is observed Hot wall q = unif[0. 9, 1. 1] Materials Process Design and Control Laboratory

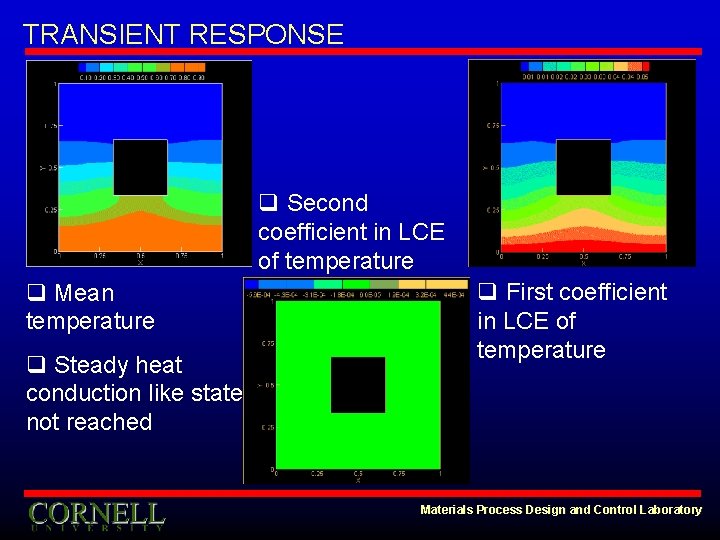
TRANSIENT RESPONSE q Second coefficient in LCE of temperature q Mean temperature q Steady heat conduction like state not reached q First coefficient in LCE of temperature Materials Process Design and Control Laboratory

CAPTURING UNSTABLE EQUILIBRIUM q 1600 bilinear elements, 5 th order Legendre chaos expansion for velocity and pressure, preconditioned GMRES Cold wall q = 0 Insulated q Time [0, 1. 5] q Time step [0. 002] q Rayleigh number unif[1530, 1870] q Prandtl number [6. 95] Cold wall q = 1 q Support-space mesh [10 elements] q Simulation about critical Rayleigh number [Ghanem JCP] q Failure of GPCE approach and use of support-space Materials Process Design and Control Laboratory

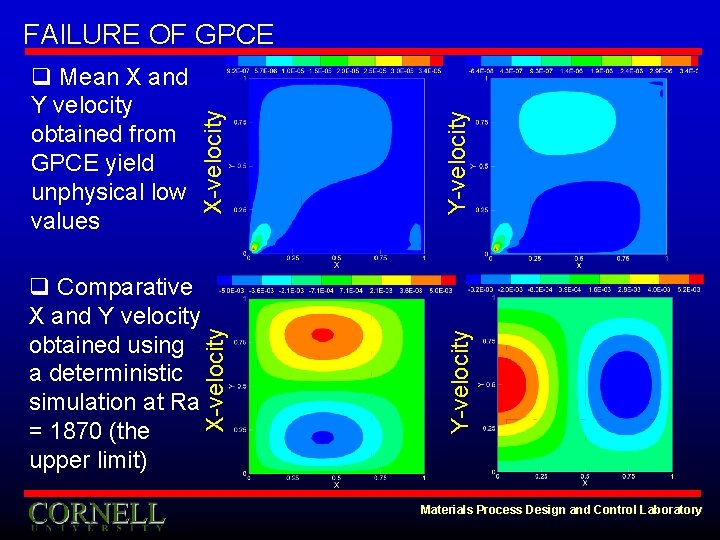
Y-velocity q Comparative X and Y velocity obtained using a deterministic simulation at Ra = 1870 (the upper limit) X-velocity q Mean X and Y velocity obtained from GPCE yield unphysical low values X-velocity FAILURE OF GPCE Materials Process Design and Control Laboratory

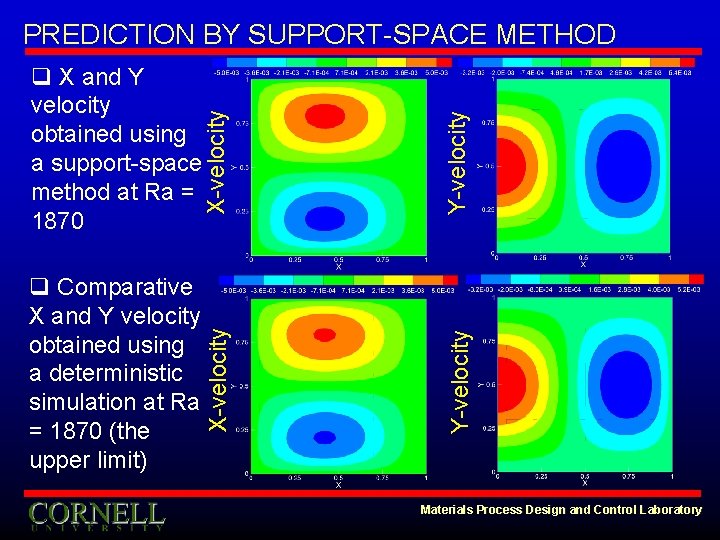
Y-velocity q Comparative X and Y velocity obtained using a deterministic simulation at Ra = 1870 (the upper limit) X-velocity q X and Y velocity obtained using a support-space method at Ra = 1870 Y-velocity PREDICTION BY SUPPORT-SPACE METHOD Materials Process Design and Control Laboratory

EXPLICIT SUBGRID MODELING q Explicit subgrid modeling q Stochastic elliptic equation – VMS implementation q Numerical examples Materials Process Design and Control Laboratory

MODEL MULTISCALE ELLIPTIC EQUATION Boundary Domain in on q Multiple scale variations in K q K is inherently random [property predictions are at best statistical] Crystal microstructures q Composites q Diffusion processes Permeability of Upper Ness formation Materials Process Design and Control Laboratory

VMS [VARIATIONAL FORMULATION] [V] Find such that, for all q [V] denotes the full variational formulation q U and V denote appropriate function spaces for the multiscale solution u and test function v respectively q VMS hypothesis: Exact = coarse + fine q Induced function space decomposition [Hughes 1995] Materials Process Design and Control Laboratory

VMS [COARSE AND SUBGRID SCALES] and the induced function space Using decomposition Find and such that, for all Coarse [V] Subgrid [V] q Solve subgrid [V] using Greens' functions, PU and other q Substitute the subgrid solution in coarse [V] Materials Process Design and Control Laboratory

DEFINITIONS AND DISCRETIZATION q Assume a finite element discretization of the spatial region D into Nel. C coarse elements q Each coarse element is further discretized by a subgrid mesh with Nel. F elements q In each coarse element, the coarse solution u. C can be approximated as nbf = number of spatial finite element basis functions in each coarse element PC = number of terms in the GPCE of coarse solution Materials Process Design and Control Laboratory

DEFINITIONS AND DISCRETIZATION [CONTD] All basis function problems solved here Coarse mesh Subgrid mesh for element EC Materials Process Design and Control Laboratory

SOLUTION OF HOMOGENEOUS [V] CONTD q Considering the following finite element – GPCE representation for coarse solution u. C q The subgrid solution can be represented as follows q Since represents subgrid variations, a nonlinear coarse scale mapping, a higher order GPCE is used [implies more terms in GPCE of ] Materials Process Design and Control Laboratory

SOLUTION OF HOMOGENEOUS [V] CONTD q Now, we have q Thus, we end up with (Nmax+1) homogeneous subgrid problems in each coarse element D(e) q Following representation is used for approximation nbf = number of spatial finite element basis functions in each element defined on the subgrid mesh PF = number of terms in the GPCE. Also, PF >PC Materials Process Design and Control Laboratory

SOLUTION OF AFFINE [V] Affine [V] q This affine correction is unique to the VMS formulation [Arbogast et al] and is not obtained in Ms. FEM type of formulations q Crucial in case of localized sources and sinks q Again, similar to the homogeneous [V], we have q This affine correction solution has no dependence on coarse scale behavior q We solve this equation on each coarse element with zero boundary conditions Materials Process Design and Control Laboratory

SOLVING REDUCED PROBLEM Mapping element edge Subgrid mesh n s q Each coarse element edge is mapped to a line grid q Line grid yields coordinates (s – along the line grid, n – normal to line grid) q The reduced problem specified below is solved on the line grid Materials Process Design and Control Laboratory

SOLVING REDUCED PROBLEM 0 GPCE coefficients of coarse + subgrid BC 0 1 0 0 0 0 Materials Process Design and Control Laboratory

DESCRIPTION OF NUMERICAL PROBLEMS Coarse element D(e) Subgrid mesh q Based on boundary conditions used and subgrid problems solved, we have three studies Ms. FEM-L q Linear boundary conditions are used VMS-Os Ms. FEM-Os q Reduced solution as BC q No affine correction q Affine correction explicitly solved Materials Process Design and Control Laboratory

FEM FOR HOMOGENEOUS [V] q Thus in each coarse element EC, we can solve for the subgrid basis functions as follows q Note that we solve for the sum of coarse + subgrid basis functions q The boundary conditions for this equation are obtained as the solution of the reduced problem on coarse element edges q DOF for the problem = (Nno-subgrid)(PF+1) Materials Process Design and Control Laboratory

DISTINCTIONS BETWEEN FUNCTION SPACES q The number of functions spanning the subgrid approximation space is given by the tensor product q The subgrid basis functions however are a subset of these functions and hence do not contain all subgrid information q Is there a contradiction? Actual solution Subgrid scale solution h Coarse scale solution q Idea of VMS is only to solve the subgrid approximately q We just look in an intelligent manner, a subset of the fine function space wherein the solution is best represented Materials Process Design and Control Laboratory

STOCHASTIC [CASE I] PSEUDO-PERIODIC MEDIA q uniformly distributed diffusion coefficient K 0 Materials Process Design and Control Laboratory

STOCHASTIC [CASE I] RESULTS FEM Ms. FEM-Os VMS-Os U 0 U 1 U 2 Materials Process Design and Control Laboratory

STOCHASTIC [CASE I] ERROR MEASURES q L-inf error was calculated on the mean value q Again, VMS is consistently better than Ms. FEM-Os. Materials Process Design and Control Laboratory

STOCHASTIC [CASE I] EFFECT OF PC TERMS q We have assumed that the fine scale solution has more PC terms in its expansion Linf error L 2 error q While reconstructing the fully resolved solution from the fine scale solution, we can only reconstruct up to the PCC terms. Beyond those terms, the fine scale solution is no longer a oneto-one map, hence, we see abnormalities (still equal in L-2) Materials Process Design and Control Laboratory

q Transient multiscale heat conduction q VMS implementation q Formulation 1: no subgrid time evolution q Formulation 2: quasi-static subgrid Materials Process Design and Control Laboratory

MODEL MULTISCALE DIFFUSION EQUATION Boundary Domain in on q Multiple scale variations in K q K is inherently random [property predictions are at best statistical] Chip cooling and diffusion heat transfer Diffusion, heat conduction in microstructural lengths scale, composites q First step towards a multiscale industrial process simulator Materials Process Design and Control Laboratory

VMS [VARIATIONAL FORMULATION] [V] Find such that, for all q [V] denotes the full variational formulation q U and V denote appropriate function spaces for the multiscale solution u and test function v respectively q VMS hypothesis: Exact = coarse + fine q Induced function space decomposition [Hughes 1995] Materials Process Design and Control Laboratory

VMS [COARSE AND SUBGRID SCALES] and the induced function space Using decomposition Find and such that, for all Coarse [V] Subgrid [V] q Solve subgrid [V] using Greens' functions, PU and other q Substitute the subgrid solution in coarse [V] Materials Process Design and Control Laboratory

ASSUMPTIONS q Formulation 1 q The projection of time derivative ut on the subgrid function space is zero q This assumption assumes that the phenomena on the subgrid level attains equilibrium at every instant q Formulation 2 q Quasistatic subgrid solution q This renders the term (u. Ft, v. F) zero q This assumption is accurate provided the time step size used in the integration of governing equations is small Materials Process Design and Control Laboratory

DEFINITIONS q Considering the following finite element representation for coarse solution u. C q The subgrid solution u. F can be represented as follows Formulation 1 Formulation 2 q Note that in case of quasistatic subgrid scale, the subgrid solution is a map of both coarse scale solution and coarse scale time derivative of solution Materials Process Design and Control Laboratory

WHY THE CHOICE? q The alternative is to use backward Euler time discretization for the fine scale (after some algebra) q The subgrid homogeneous equation now yields q This is a tougher reaction-diffusion equation (notice that the diffusion coefficient is multiplied with a small time step size). In practical experiments, this equation yields spurious solutions Materials Process Design and Control Laboratory

SOLUTION OF SUBGRID EQUATION q For the assumptions employed for the subgrid model, we have Formulation 1 Formulation 2 q Wherein, the index a ranges from 1 to Nbf, the number of coarse basis functions in each coarse spatial sub-domain D(e) q Since the governing model is linear, the basis functions need to be estimated only in the first time step. Hence, we just solve a coarse problem for all remaining time steps!! Materials Process Design and Control Laboratory

DETERMINISTIC [CASE I] PERIODIC MEDIA K q Fully resolved solution was obtained using a 128 x 128 mesh with bilinear quad elements q Time step size = 0. 0005, duration of simulation = [0, 0. 05] Materials Process Design and Control Laboratory

RESULTS[ANIMATIONS] VMS solution FEM solution L-inf error Materials Process Design and Control Laboratory

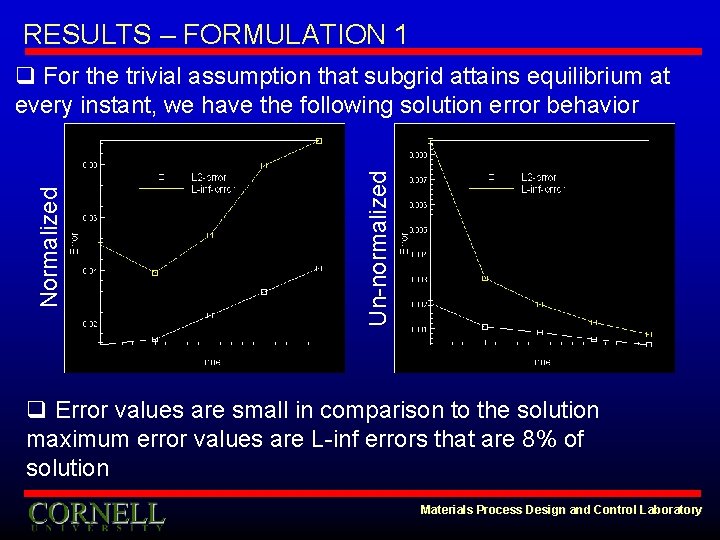
RESULTS – FORMULATION 1 Un-normalized Normalized q For the trivial assumption that subgrid attains equilibrium at every instant, we have the following solution error behavior q Error values are small in comparison to the solution maximum error values are L-inf errors that are 8% of solution Materials Process Design and Control Laboratory

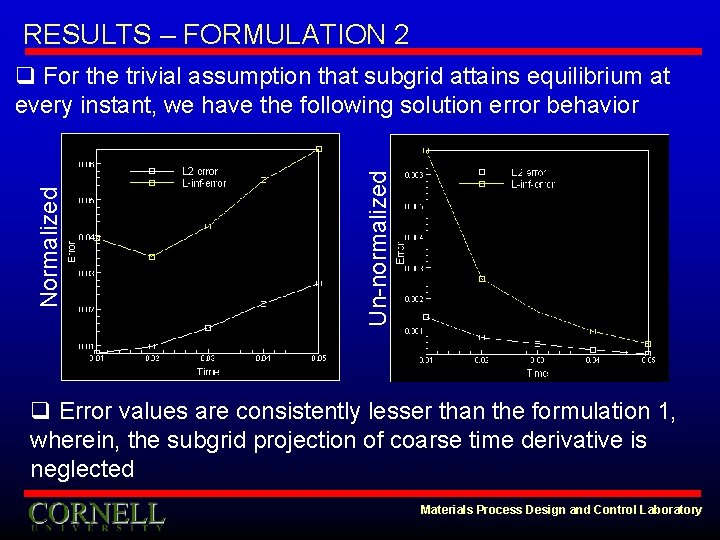
RESULTS – FORMULATION 2 Un-normalized Normalized q For the trivial assumption that subgrid attains equilibrium at every instant, we have the following solution error behavior q Error values are consistently lesser than the formulation 1, wherein, the subgrid projection of coarse time derivative is neglected Materials Process Design and Control Laboratory

q Open issues in VMS q Difficulties in adapting to convection-diffusion q Nonlinearities q Adaptive VMS formulations q Non-quasistatic subgrid phenomena q Open issues in stochastic modeling q Compatibility of statistics across length scales q Transferring information from further lower scales Materials Process Design and Control Laboratory

CONVECTION-DIFFUSION [DIFFICULTIES] q Need to make transition from diffusion problems to convection-diffusion problems q Advection skew to a mesh shown q. Information propagates along the characteristics q Most practical problems have extremely low diffusion. A further stabilized subgrid formulation may be required q Boundary conditions applied to subgrid problems have to be enhanced Materials Process Design and Control Laboratory

BOUNDARY CONDITIONS q In diffusion type problems, a reduced Edge mapped problem is solved in the to a line grid q The reduced problem is the set of governing differential equations with Internal layers derivatives normal to the proportional to diffusion element edge equated to coefficient zero A typical coarse element q In convection-diffusion problems, the multidimensional layers that form in the solution should be captured by the basis function [not possible with current oscillatory BC approach] Materials Process Design and Control Laboratory

NONLINEARITY AND ADAPTIVITY q Adaptive VMS [Larson, Chalmers preprint] q Nonlinear Ms. FEM [Hou] Multiscale regions Transition regions q calculate error in solution, dual of solution to find regions of varying physics Coarse regions q calculate coarse scale solution by iterative methods q Calculation of basis functions Very fine subgrid mesh Coarser subgrid mesh q Inexact Newton methods for solving subgrid problems Materials Process Design and Control Laboratory

STATISTICS ACROSS LENGTH SCALES Lower order descriptors VMS linkage q VMS Coarse then uses series expansions to characterize uncertainty propagation across the coarse and subgrid scales q Statistical Subgrid information received via MAXENT approach – that PDF that maximizes entropy q Simulations Lower scales are usually discrete q Need to describe statistics and upscale statistical information q Governing equations not necessarily PDEs Materials Process Design and Control Laboratory