A Software for Visualization and Animation in Mathematics

A Software for Visualization and Animation in Mathematics Eberhard Malkowsky Vesna Veličković Seminar o nastavi matematike i računarstva Niš, 14, 15 February, 2003

Introduction Visualization and animation play an important role in the understanding of mathematics. Therefore they should extensively be used in teaching. Here we present our own software for visualization and animation in mathematics.

The Software We use our own software [1]. The software is aimed at visualizing mathematics and to support teaching and research. It has applications to the natural and engineering sciences. It is open, that is the source files are available to the users. Thus it can be extended. It uses OOP. The programming language is PASCAL.

References [1] E. Malkowsky, W. Nickel, Computergrafik in der Differentialgeometrie, Vieweg-Verlag Braunschweig/Wiesbaden, 1993

The Main Principles of the Software 1. Strict separation of geometry and the technique of drawing 2. Line graphics 3. Central projection 4. Independent visibility check

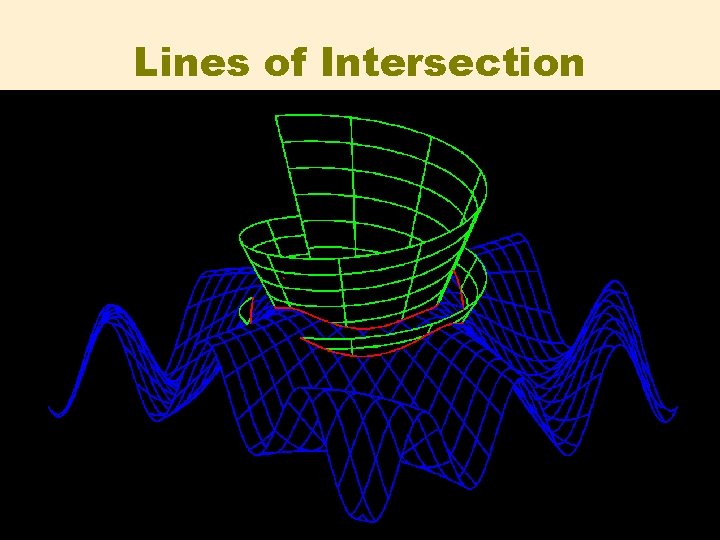
Lines of Intersection

Level Lines

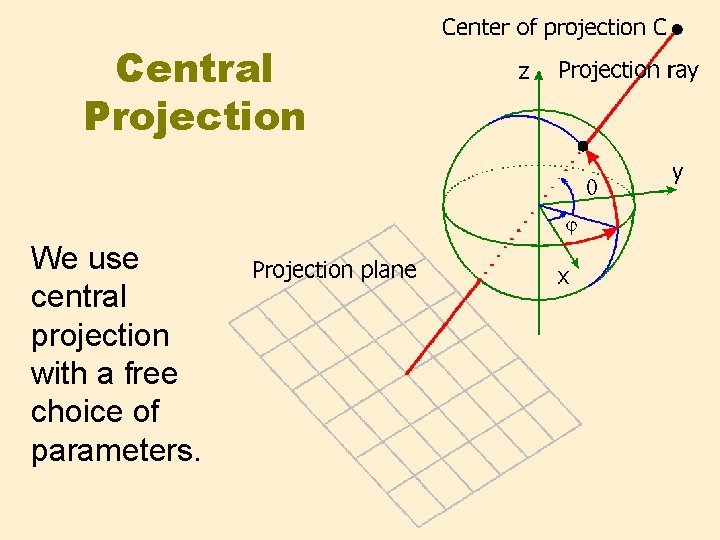
Central Projection We use central projection with a free choice of parameters.

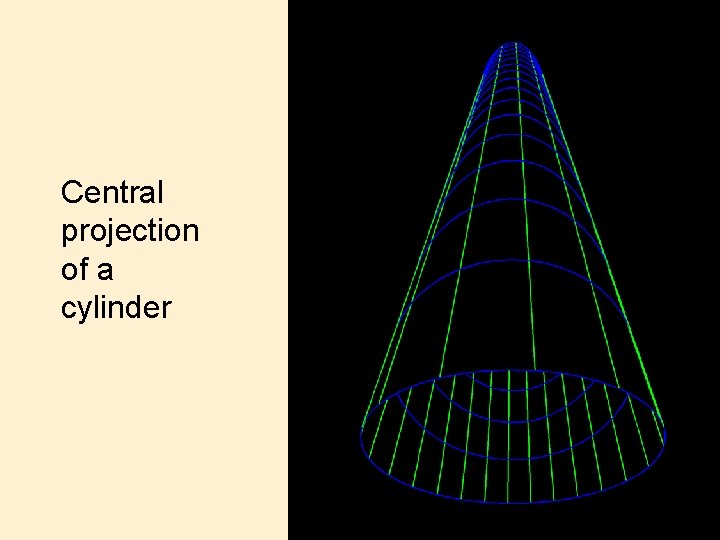
Central projection of a cylinder

Independent Visibility Check • • Independent procedure Check Immediate analytical test Interpolation to close occasional gaps Dotting or omitting invisible parts

Dandelin’s Spheres

Dandelin’s Spheres

Distance The usual distance of O and P is (1). It is called Euclidean distance.

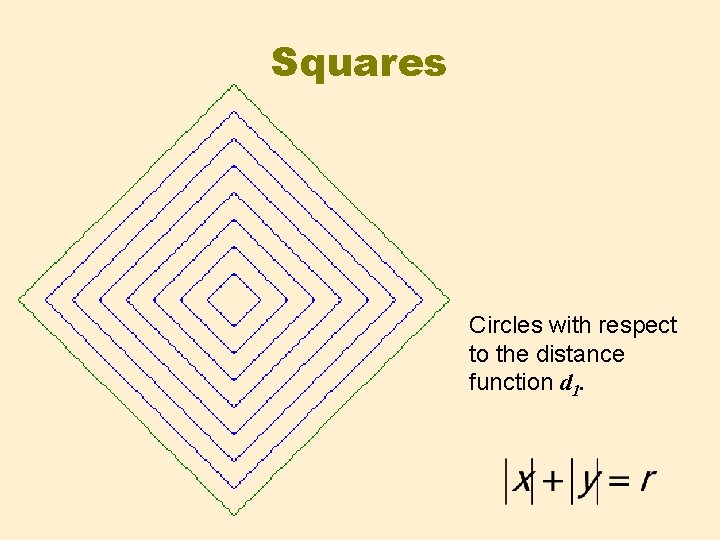
Circles The points of a circle have a constant distance from its centre. If we take this as a definition of a circle then its shape depends on the choice of the distance function.

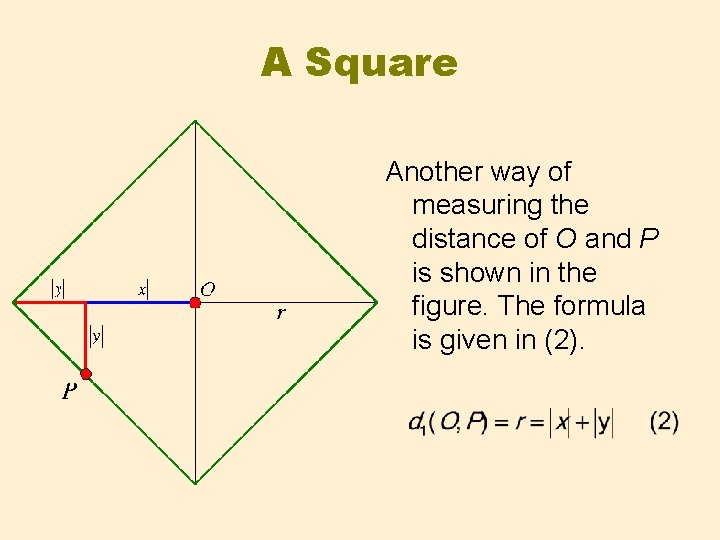
A Square Another way of measuring the distance of O and P is shown in the figure. The formula is given in (2).

Squares Circles with respect to the distance function d 1.

Generalizations More generally we consider distance functions dq with q>0 given by

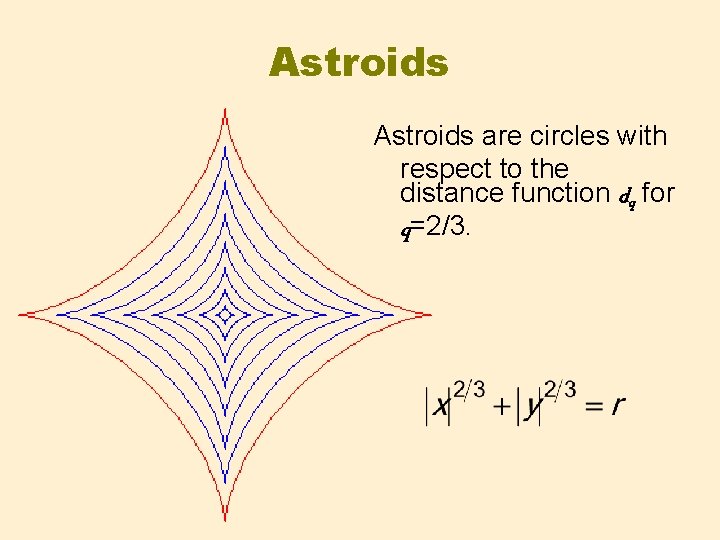
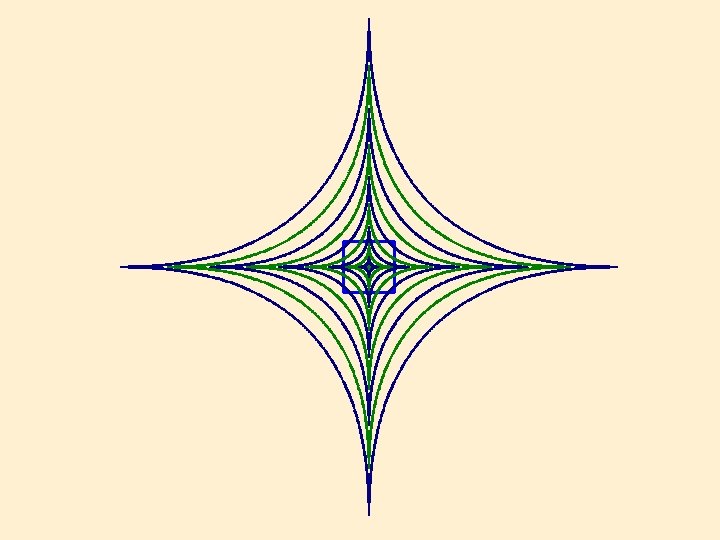
Astroids are circles with respect to the distance function dq for q=2/3.

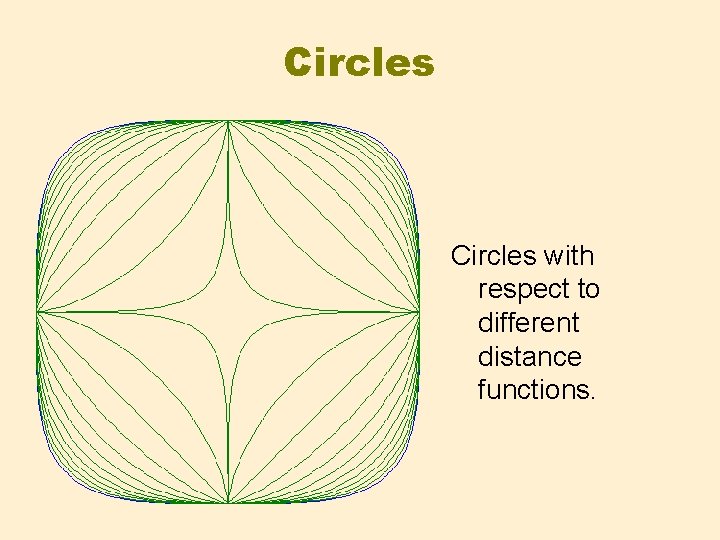
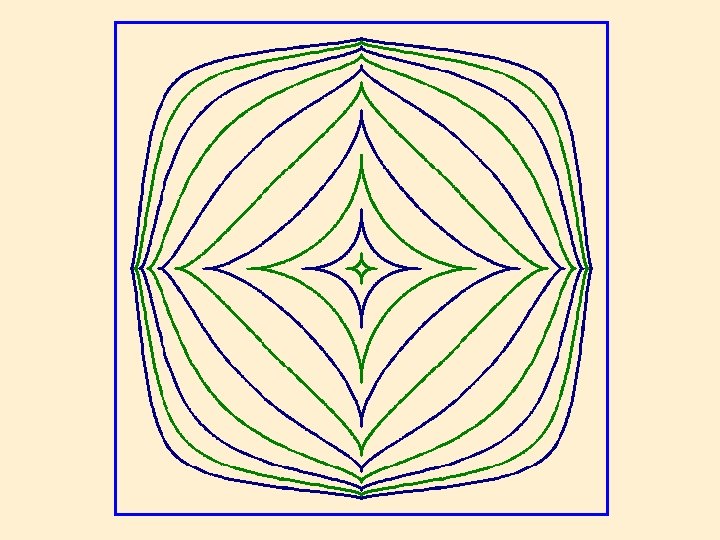
Circles with respect to different distance functions.

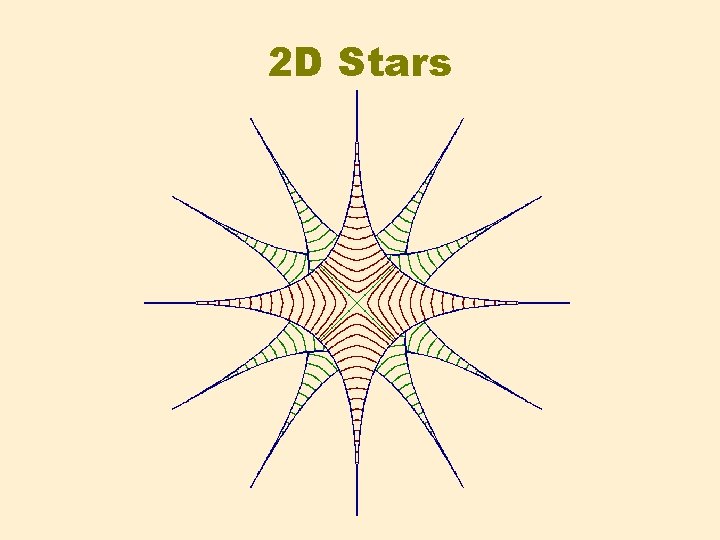
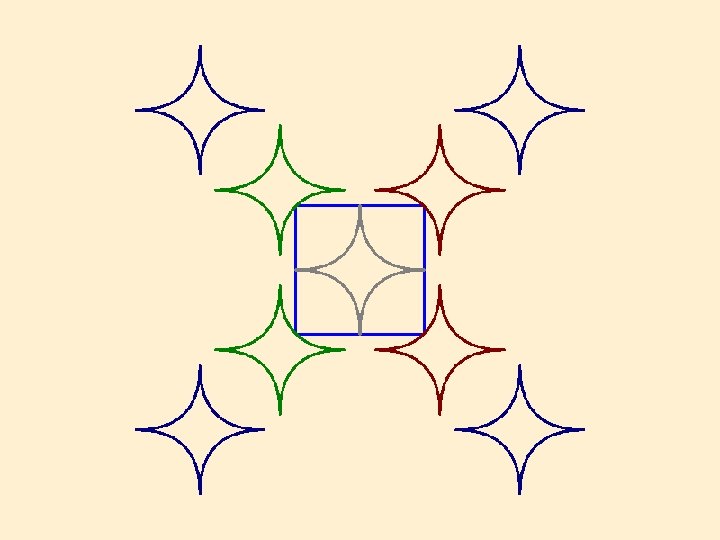
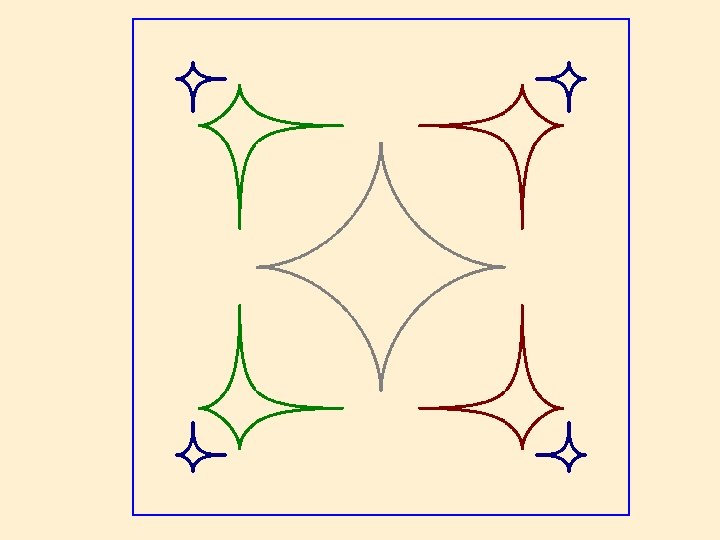
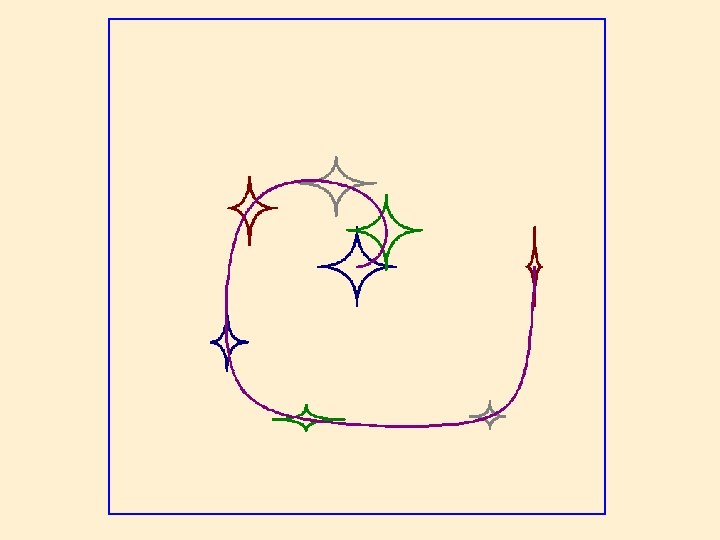
2 D Stars

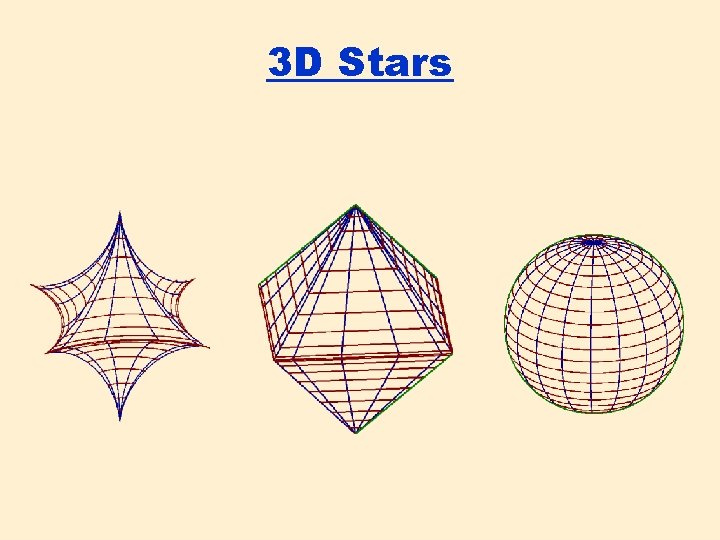
3 D Stars

Introducing a Metric If X is a set, Y a metric space with d and is a one-to-one map Then a metric can be defined on X by That is

A Map From a Rectangle Onto the Plane Let The maps

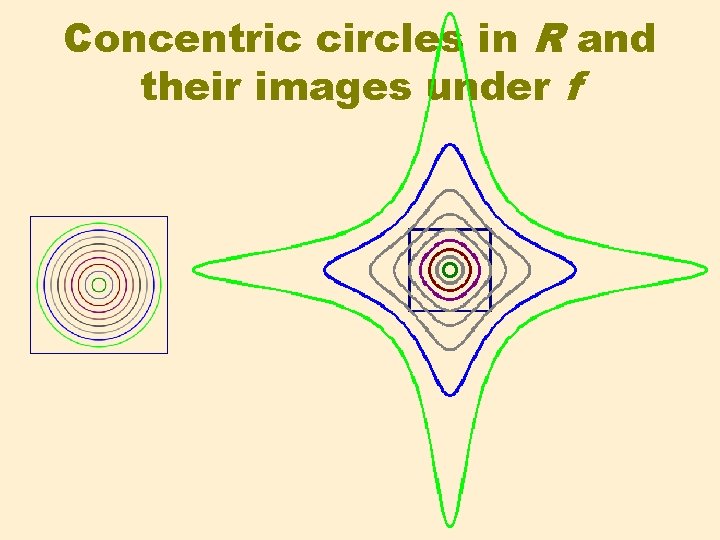
Concentric circles in R and their images under f

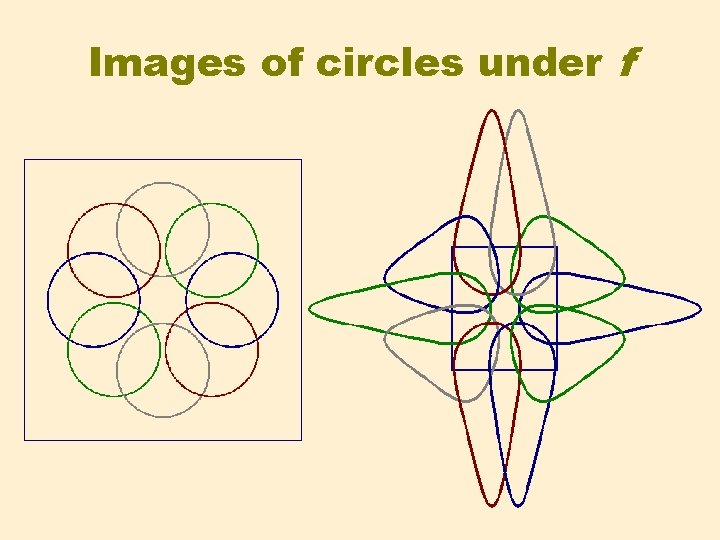
Images of circles under f

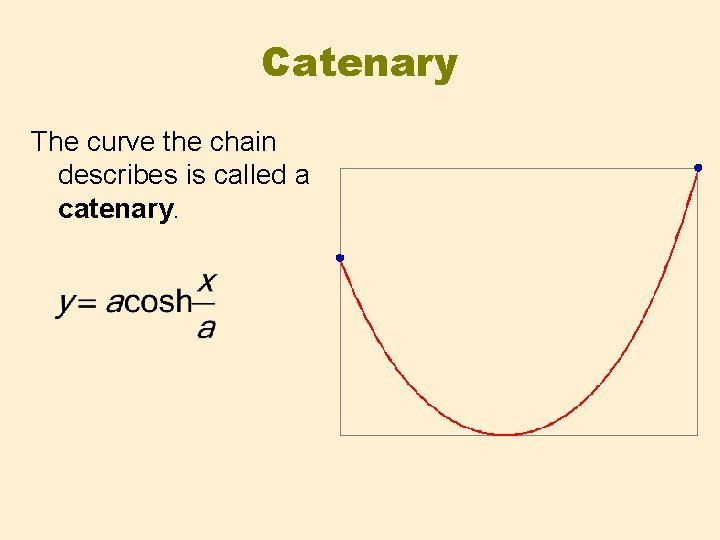
Chain It is a well known fact that, if we hold a chain at its ends and let it hang freely then it hangs in a shape which looks very much like a quadratic parabola.

Catenary The curve the chain describes is called a catenary.

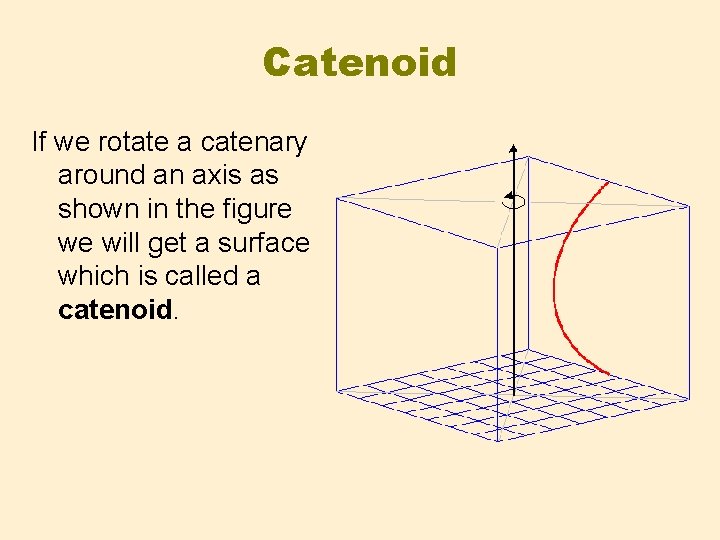
Catenoid If we rotate a catenary around an axis as shown in the figure we will get a surface which is called a catenoid.

Catenoid

Minimal Surfaces Let two curves be given. A minimal surface is a surface which has minimal surface area of all the surfaces bounded by the given curves. A Catenoid is a minimal surface. Its boundary are two circles.

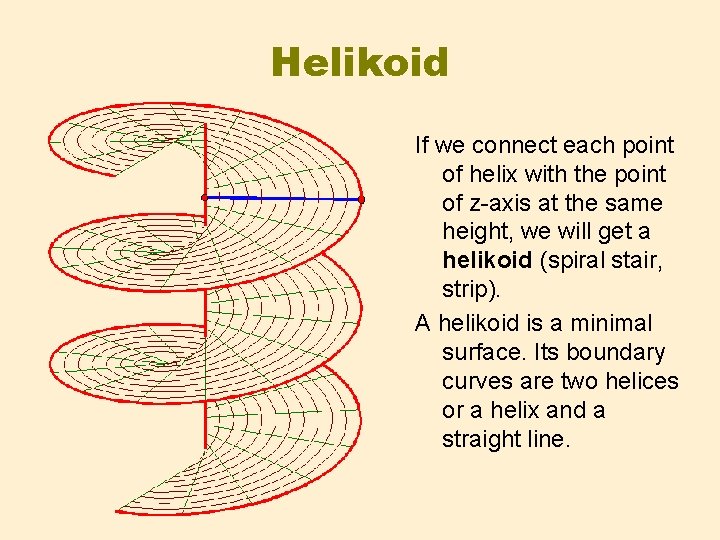
Helikoid If we connect each point of helix with the point of z-axis at the same height, we will get a helikoid (spiral stair, strip). A helikoid is a minimal surface. Its boundary curves are two helices or a helix and a straight line.

From a Catenary to a Helikoid There is a continuous transformation from a catenoid to a helikoid. All surfaces in between are minimal surfaces.

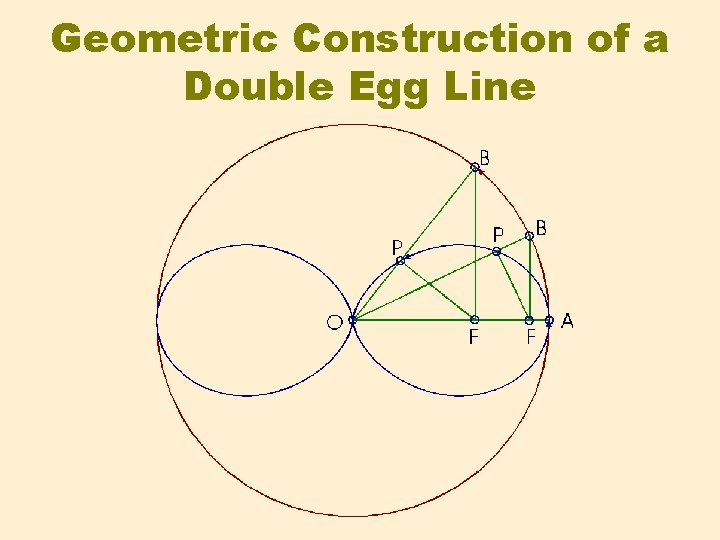
Geometric Construction of a Double Egg Line

Geometric Construction of a Rosette

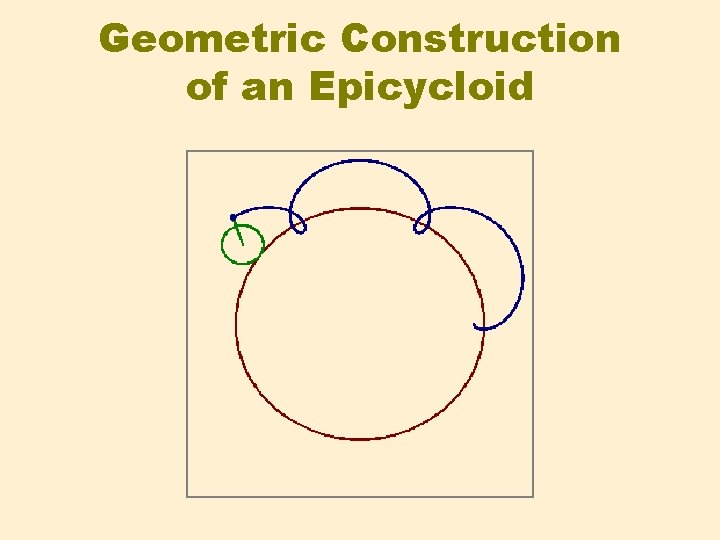
Geometric Construction of an Epicycloid

Deformations of • Torus to Double Egg (Torus to Double Egg) • Torus (Torus) • Torus to Lemniscate (Torus to Lemniscate)

Rotation • Rotation of a potential surface (Rotation of a potential surface)