A simple statistical model for deciphering the cdc

A simple statistical model for deciphering the cdc 15 synchronized yeast cell cycle-regulated genes expression data Ker-Chau Li , Robert Yuan Statistics, UCLA Ming Yan Biochemistry , UCLA

The goal of this study is to demonstrate how simple statistical models can be employed for helping the organization and explanation of complex gene expression patterns

Outlines • • Introd : Micro-array and cell-cycle Data : cdc 15 experiment A statistical model Phase determination Comparison with Spellman et al(1998) Regularly oscillated genes Further discussion

Micro. Array • Allows measuring the m. RNA level of thousands of genes in one experiment -- system level response • The data generation can be fully automated by robots • Common experimental themes: – Time Course – Mutation/Knockout Response

Yeast Cell Cycle (adapted from Molecular Cell Biology, Darnell et al)

The data set available at http: cellcycle-www. standford. edu We focus on one experiment in which a strain of yeast(cdc 15 -2) was incubated at a high temperature(35 degrees C) for a long time, causing cdc 15 arrest. Cells were then shifted back to a low temperature( 23 degrees C) and the monitoring of gene expression is taken every 10 min for 300 min.

Data from some chips are not available We concentrate on those from the 19 Consecutive time points from 70 mins To 250 mins 24 Time points: (mins) 10 30 50 70 80. . . 240 250 270 290 -----> 10 mins apart Use of full data will be discussed later. Genes with missing values are also Deleted There are 4530 genes remaining The data can be represented by a 4530 by 19 matrix

Example of the time curve: Histone Genes: (HTT 2) ORF: YNL 031 C Time course:

YKL 164 C YNL 082 W

Preliminary study with two-way anova This is to investigate the constancy of average expression Level over the time for each gene and the constancy of The average expression level over all genes at each time Point. > cdc 15 Factor gene time residual total df | 4529 | 18 |81522 |86069 | | SS 5. 2408 E+2 2. 9745 E+2 1. 4701 E+4 1. 5522 E+4 | | | MS 1. 1572 E-1 1. 6525 E+1 1. 8033 E-1 | | F 6. 4169 E-1 9. 1638 E+1 Gene insignificant Time appears statistically significant; But …………(next slide)

Column mean (Time) from Anova result The values are small The expression level is log_2 of ratio of red/green Red = light intensity for red channel - “noise” Green = light intensity of green channel - “noise” Red channel = m. RNA from cells at one time point Green channel =m. RNA from unsynchronized cells. 5 fold increase = log_2 1. 5=. 585 ; 2^. 15 =1. 11=. 11 fold increase

A statistical model • Motivation : modeling each curve with simple functions such as linear, quadratic, sine, cosine appears reasonable but inflexible; • Parsimony and accuracy can be gained if basis curves are chosen by data themselves • The model : each gene expression curve =

The model -continued The errors have mean zero, uncorrelated , same variance cross the time; But the variance may depend on genes (This is important) It turns out that we can find the basis functions from an application of PCA. (see pdf file for pca)

Enhanced PCA for curve fitting Choose the number of basis curves by eigenvalues l Assess the goodness of each curve fitting by R-squared and by residual sum of squares l Identify genes that comply well to the model l Interactive plotting helps resetting userspecified parameters l

PCA: For a list of vectors, PCA could be used for finding the common basis based on the scaling matrix. Covariance Matrix: The directions found will have highest variance along those directions. Find the directions by eigenvalue decomposition: Model the curves by the PCA directions: Here, we chose first three PCA directions as our basis.

1 st PCA direction 2 nd PCA direction 3 rd PCA direction Eigenvalues

1. Compliance Check: Reject if (Corr. Coff between fit and observed <. 75 And error s. d. Bigger than. 70 , which is equivalent to. 5 fold increase. ) 2. Cycle Component Check: Reject if 3. Smoothness Check: Reject if

Noncompliance genes (41). High overall expression levels. May or may not show cycle patterns … Recommendation : inspect each gene separately

Phase determination • The second and the third basis curves show clear cycle patterns. The third basis appears to be a 40 min-delayed version of the second basis, with an R-squared value of. 78 • Linear combinations of these two basis curves show a variety of expression patterns.

Construction of A Compass plot • • Use of known cycle-regulated genes Compliance checking with RSS/R^2 plot Cycle- exhibition checking with projection angles Coherent pattern checking by ANOVA • ( A list of 104 known genes with 6 groups)

Phases of genes: Identify the phases of genes: Prior Knowledge: There were 104 know genes whose phases were determined by traditional experiment methods. Known genes: There are 6 groups of genes. SCB (G 1 phase) MCB (G 1 phase) Histone (S phase) S/G 2 phase G 2/M phase M/G 1 phase The noncompliance genes and without significant cycle components are excluded The group of genes, SCB, are also excluded due to the inconsistent patterns within their expression vectors.

82 non-missing known phase genes Remove genes with insignificant cycle component Points obtained by normalizing the loading coeff. for 2 nd and 3 rd bases to unit length

Late G 1, SCB regulated genes:

Compass plot for phase assignment Histone genes S G 1 S/G 2 M/G 1 G 2/M

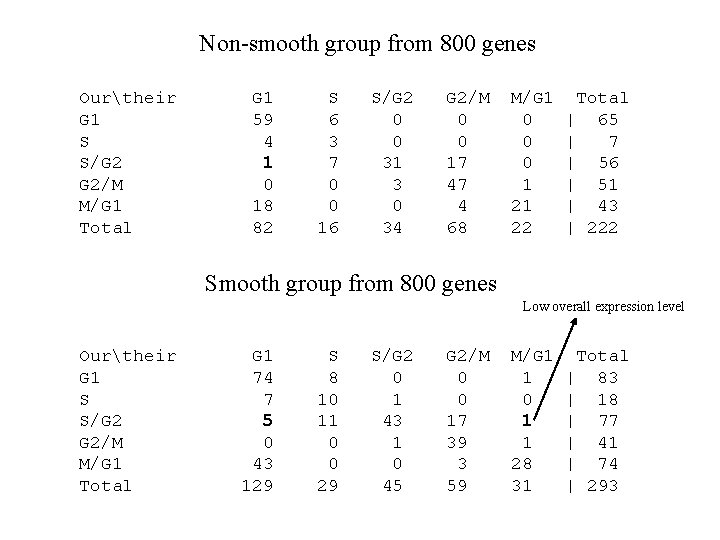
Phase Assignment Smooth Non-smooth G 1 108 S 31 S/G 2 352 G 1 103 S S/G 2 27 255 90 295 M/G 1 165 G 2/M 239 M/G 1 90 G 2/M

Comparison • For the 800 cell-regulated genes classified by Spellman et al, we re-classified them with our method. If a gene does not comply with our model or does not have significant second or third regression coefficients, we would not assign the phase. • Contingency tables of mismatched and unclassified cases.

A non-compliance gene YJL 159 W : Spellman et. al’s Score : 10. 86 R 2: 0. 36273 (M/G 1) RSS: 14. 15322 Angle: -2. 43803 Least Squares Estimates: Constant Variable 0 Variable 1 Variable 2 -4. 794002 E-16 (0. 222846) 1. 28464 (0. 971364) -2. 04016 (0. 971364) -1. 49779 (0. 971364) Black: data curve Red : fitted curve (full model) Blue : fitted curve (cyclic model) Locus_info: Other_name PIR 2 YJL 159 W CCW 7 ORE 1 Gene_class HSP Gene_Info HSP 150 Gene_product Heat shock protein, secretory glycoprotein Function cell wall structural protein Cellular_Component cell wall Process cell wall organization and biogenesis Phenotype Null mutant is viable Locus_notes 14 HSP 150 has also been called gp 400 Position_info: Chromosome X ORF_name YJL 159 W

An example of our non-compliance gene Locus_info: Other_name YDR 055 W : Spellman et. al’s Score : 7. 266 R 2: 0. 30136 (M/G 1) RSS: 7. 94018 Angle: -2. 81396 (Insig. Coef. ) Least Squares Estimates: Constant Variable 0 Variable 1 Variable 2 -5. 428720 E-16 (0. 166914) 1. 47329 (0. 727561) -1. 07451 (0. 727561) -0. 316032 (0. 727561) Black: data curve Red : fitted curve (full model) Blue : fitted curve (cyclic model) Gene_class PST Gene_Info PST 1 Description Protoplasts-secreted Gene_product The gene product has been detected among the proteins secreted by regenerating protoplasts Phenotype Viable Position_info: Chromosome IV ORF_name YDR 055 W

An example of gene non-compliance YNL 082 W : Spellman et. al’s Score : 4. 843 R 2: 0. 229191 (G 1) RSS: 18. 247480537500003 Least Squares Estimates: Constant (0. 253035) Variable 0 Variable 1 Variable 2 -6. 087129 E-16 1. 51725 -1. 74757 0. 263945 (1. 10295) Black: data curve Red : fitted curve (full model) Blue : fitted curve (cyclic model)

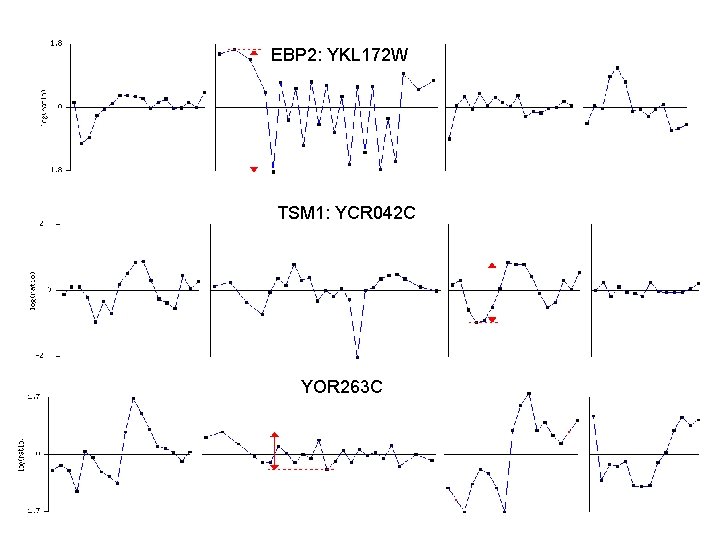
Top 10 scores and gene names from insignificant Cycle component group 3. 69 3. 85 3. 874 4. 022 4. 048 4. 13 4. 41 5. 047 6. 28 6. 716 "YOR 263 C" "YOR 320 C" "YGR 035 C" "YCR 042 C" "YPR 019 W” "YJL 194 W" "YJR 010 W" "YEL 068 C" "YGR 124 W" "YKL 172 W" 78 genes score higher than 6. 716; 188 genes score higher than 4. 022 213 genes score higher than 3. 69 Yet these genes appear very bumpy; see next slide

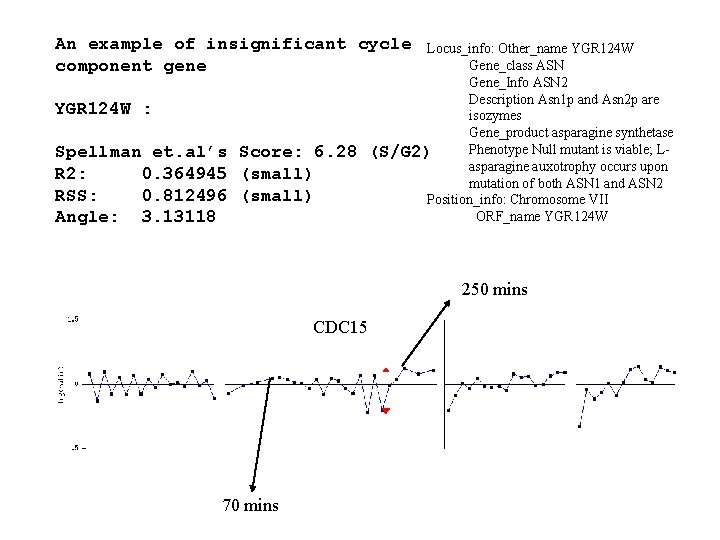
An example of insignificant cycle component gene YGR 124 W : Spellman et. al’s Score: 6. 28 R 2: 0. 364945 (small) RSS: 0. 812496 (small) Angle: 3. 13118 Locus_info: Other_name YGR 124 W Gene_class ASN Gene_Info ASN 2 Description Asn 1 p and Asn 2 p are isozymes Gene_product asparagine synthetase Phenotype Null mutant is viable; L(S/G 2) asparagine auxotrophy occurs upon mutation of both ASN 1 and ASN 2 Position_info: Chromosome VII ORF_name YGR 124 W 250 mins CDC 15 70 mins

EBP 2: YKL 172 W TSM 1: YCR 042 C YOR 263 C

Non-smooth group from 800 genes Ourtheir G 1 S S/G 2 G 2/M M/G 1 Total G 1 59 4 1 0 18 82 S 6 3 7 0 0 16 S/G 2 0 0 31 3 0 34 G 2/M 0 0 17 47 4 68 M/G 1 0 0 0 1 21 22 Total | 65 | 7 | 56 | 51 | 43 | 222 Smooth group from 800 genes Low overall expression level Ourtheir G 1 S S/G 2 G 2/M M/G 1 Total G 1 74 7 5 0 43 129 S 8 10 11 0 0 29 S/G 2 0 1 43 1 0 45 G 2/M 0 0 17 39 3 59 M/G 1 1 0 1 1 28 31 Total | 83 | 18 | 77 | 41 | 74 | 293

CLN 2: YPL 256 C HTA 1: YDR 225 W (S) (G 1) YJL 091 C (Phase ? ? ) CLB 4: YLR 210 W (S/G 2)

CLN 2: YPL 256 C HTA 1: YDR 225 W (S) (G 1) FKS 1: YLR 342 W (Phase ? ? ) From 5 cell CLB 4: YLR 210 W (S/G 2)

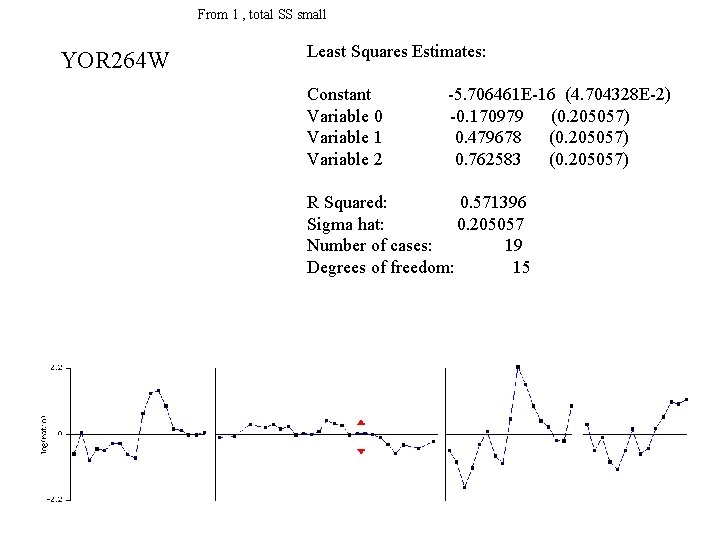
From 1 , total SS small YOR 264 W Least Squares Estimates: Constant Variable 0 Variable 1 Variable 2 -5. 706461 E-16 (4. 704328 E-2) -0. 170979 (0. 205057) 0. 479678 (0. 205057) 0. 762583 (0. 205057) R Squared: 0. 571396 Sigma hat: 0. 205057 Number of cases: 19 Degrees of freedom: 15

Oscillated genes • First curve basis is oscillating in a extremely regular way • There are over 200 genes with such regular oscillating patterns • Role unknown : Systematic error ? Common upstream promoter region ?

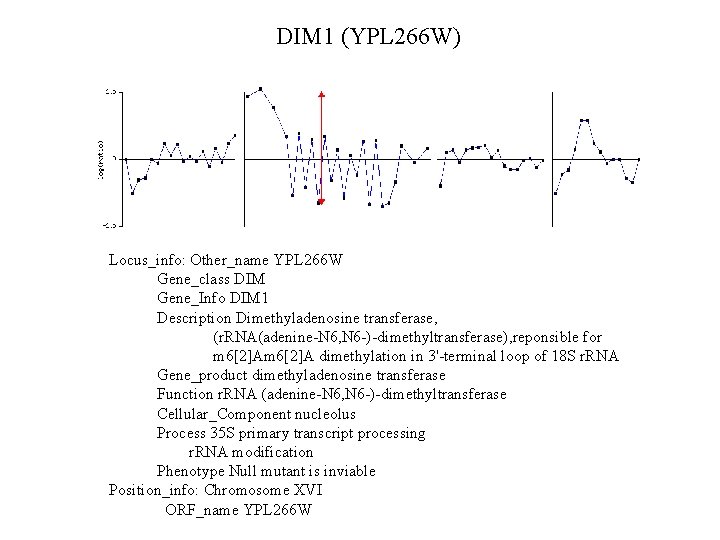
DIM 1 (YPL 266 W) Locus_info: Other_name YPL 266 W Gene_class DIM Gene_Info DIM 1 Description Dimethyladenosine transferase, (r. RNA(adenine-N 6, N 6 -)-dimethyltransferase), reponsible for m 6[2]A dimethylation in 3'-terminal loop of 18 S r. RNA Gene_product dimethyladenosine transferase Function r. RNA (adenine-N 6, N 6 -)-dimethyltransferase Cellular_Component nucleolus Process 35 S primary transcript processing r. RNA modification Phenotype Null mutant is inviable Position_info: Chromosome XVI ORF_name YPL 266 W

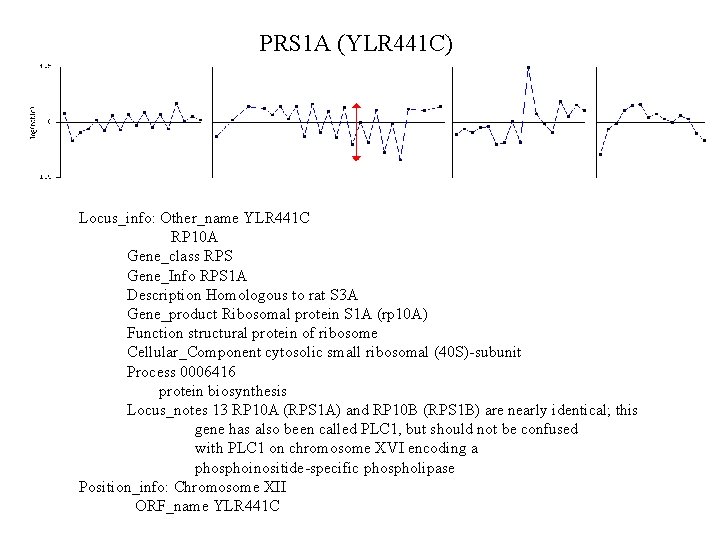
PRS 1 A (YLR 441 C) Locus_info: Other_name YLR 441 C RP 10 A Gene_class RPS Gene_Info RPS 1 A Description Homologous to rat S 3 A Gene_product Ribosomal protein S 1 A (rp 10 A) Function structural protein of ribosome Cellular_Component cytosolic small ribosomal (40 S)-subunit Process 0006416 protein biosynthesis Locus_notes 13 RP 10 A (RPS 1 A) and RP 10 B (RPS 1 B) are nearly identical; this gene has also been called PLC 1, but should not be confused with PLC 1 on chromosome XVI encoding a phosphoinositide-specific phospholipase Position_info: Chromosome XII ORF_name YLR 441 C

GLN 1: YPR 035 W One gene from non-smooth group Not in Spellman et. al. ’s list. Least Squares Estimates: Constant Variable 0 Variable 1 Variable 2 R Squared: Sigma hat: -6. 276471 E-16 (4. 762055 E-2) -2. 47649 (0. 207573) 3. 958405 E-2 (0. 207573) 1. 01860 (0. 207573) 0. 917337 0. 207573

Further discussion • • • Others who use PCA Clustering Other data set Use of SIR/PHD Without a time scale ? B-cell lymphoma data • Pathway study

. Genes with overall small expression levels could have been Removed from the beginning? ? ? YGR 231 C One gene from smooth group Not in Spellman et. al. ’s list. Least Squares Estimates: Constant Variable 0 Variable 1 Variable 2 R Squared: Sigma hat: -5. 803153 E-16 (4. 131369 E-2) -0. 156478 (0. 180082) -1. 59995 (0. 180082) -0. 623201 (0. 180082) 0. 859375 0. 180082 Total sum of squares equals to 3. 4591 which is about 71. 6 percentile among all genes. The median of the total sum of squares is 2. 27735.

THE END

YBL 002 W YER 124 C YDR 224 C YJL 159 W

YKL 163 W YKL 164 C YKL 185 W YMR 003 W

YMR 011 W YNL 160 W YDR 055 W