A Simple Linear Time Algorithm for the Domatic

A Simple Linear Time Algorithm for the Domatic Partition Problem on Strongly Chordal Graphs Shen-Lung Peng and Maw-Shang Chang Information Processing Letters, 43 (1992), pp. 297 -300. Speaker: Chuang-Chieh Lin (林莊傑) Computation Theory Laboratory Advisor: Professor Maw-Shang Chang

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 2

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 3

Dominating set • A graph of vertices D is a dominating set of a graph G = (V, E) if every vertex in V D is adjacent to a vertex in D. D = {v 1, v 4, v 5, v 7, v 8} v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 4

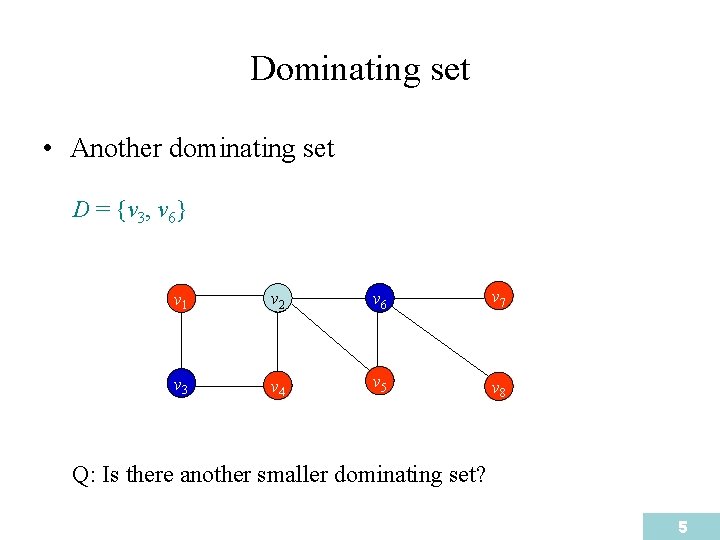
Dominating set • Another dominating set D = {v 32, v 63}, v 6} v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 Q: Is there another smaller dominating set? 5

Dominating set • What is the dominating set of the following graph? v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 6

Domatic number • The domatic number of G, denoted by d(G), is the maximum number of pairwise disjoint dominating sets in G. v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 {v 1, v 4, v 5, v 7, v 8}, {v 2, v 3, v 6} 7

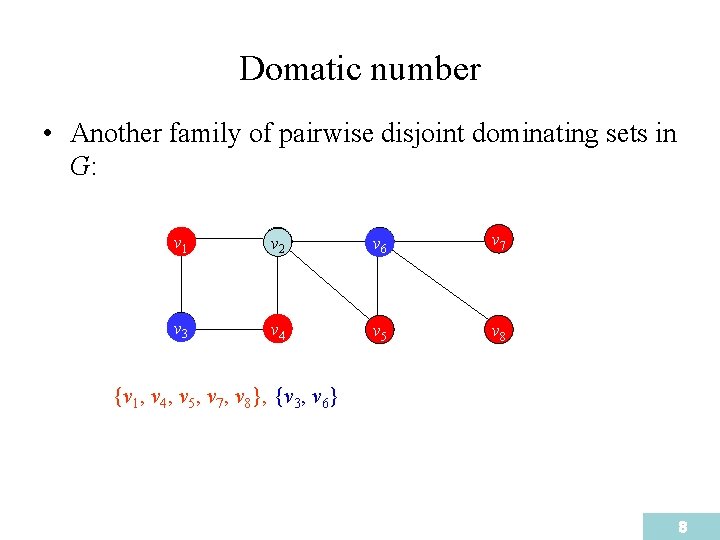
Domatic number • Another family of pairwise disjoint dominating sets in G: v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 {v 1, v 4, v 5, v 7, v 8}, {v 3, v 6} 8

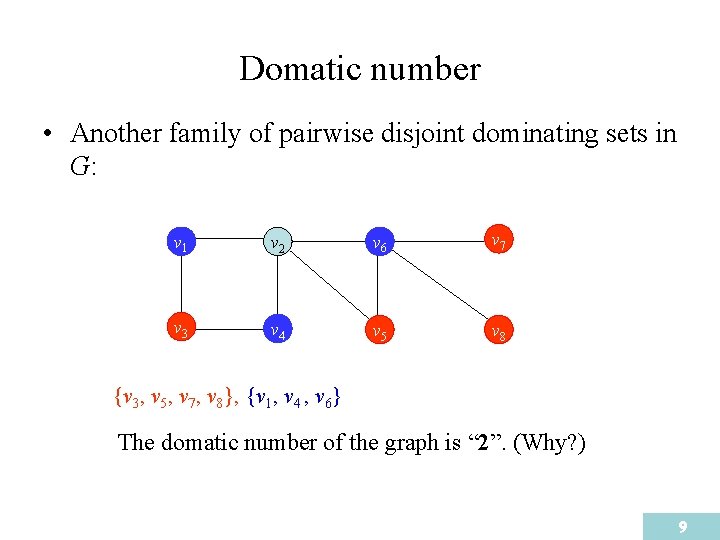
Domatic number • Another family of pairwise disjoint dominating sets in G: v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 {v 3, v 5, v 7, v 8}, {v 1, v 4 , v 6} The domatic number of the graph is “ 2”. (Why? ) 9

The domatic partition problem • The domatic partition problem is to partition V into d(G) disjoint dominating sets. v 1 v 2 v 6 v 7 v 3 v 4 v 5 v 8 {{v 1, v 4, v 5, v 7, v 8}, {v 2, v 3, v 6}} is called a domatic partition. 10

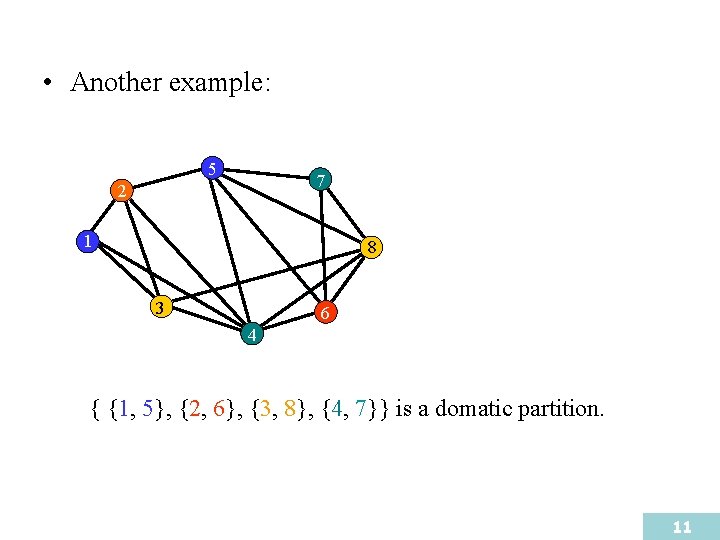
• Another example: 5 7 2 1 8 3 6 4 { {1, 5}, {2, 6}, {3, 8}, {4, 7}} is a domatic partition. 11

• Question: – Does any graph has a domatic partition? 12

• The domatic number was defined and studied by E. J. Cockayne and S. T. Hedetniemi [CH 77]. • They showed that d(G) ≤ + 1, where is the minimum degree of vertices in G. • G is domatically full if d(G) = + 1. 13

• Some special graph classes are domatically full, such as : – – – Trees, [CH 77] Cliques, [CH 77] Maximum outerplanar graphs, [CH 77] Strongly chordal graphs, [F 84] …… 14

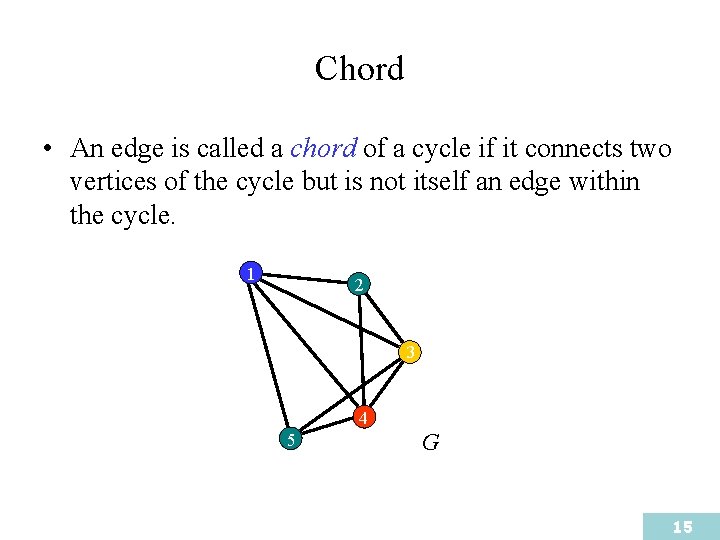
Chord • An edge is called a chord of a cycle if it connects two vertices of the cycle but is not itself an edge within the cycle. 1 2 3 4 5 G 15

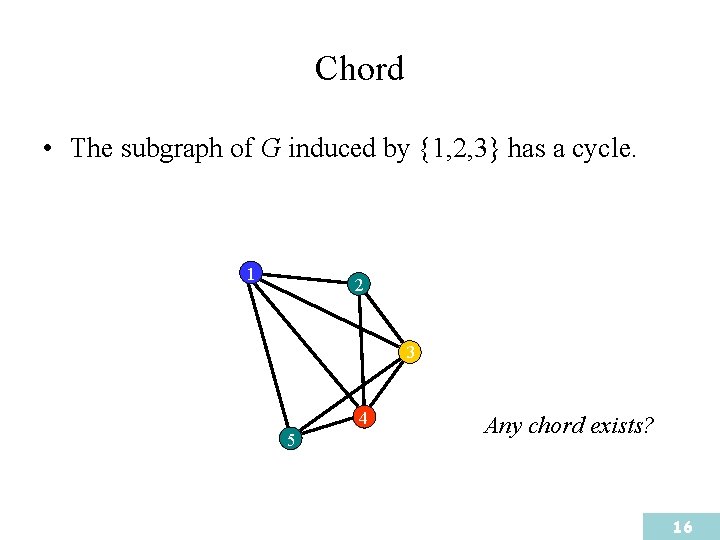
Chord • The subgraph of G induced by {1, 2, 3} has a cycle. 1 2 3 4 5 Any chord exists? 16

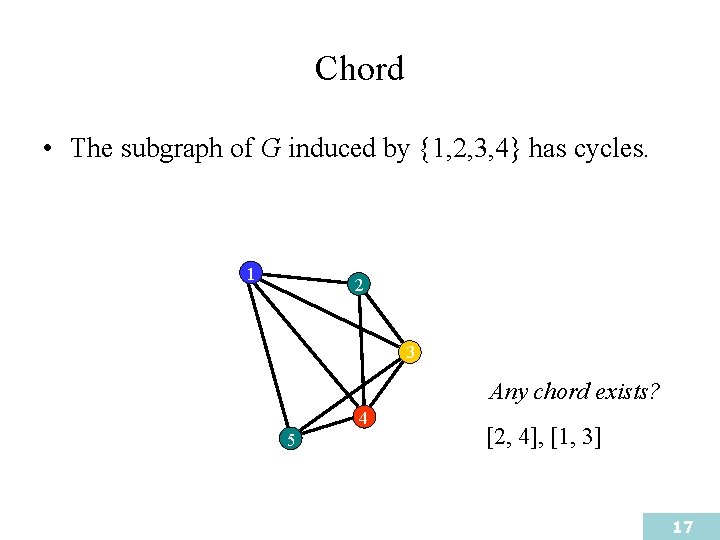
Chord • The subgraph of G induced by {1, 2, 3, 4} has cycles. 1 2 3 Any chord exists? 4 5 [2, 4], [1, 3] 17

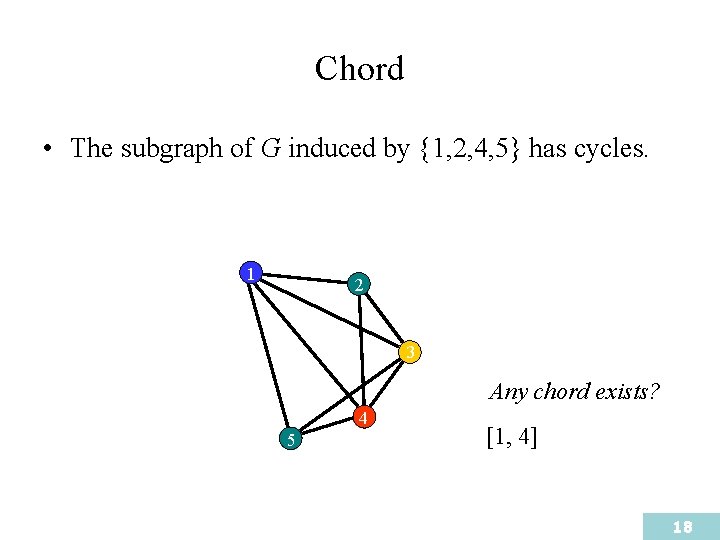
Chord • The subgraph of G induced by {1, 2, 4, 5} has cycles. 1 2 3 Any chord exists? 4 5 [1, 4] 18

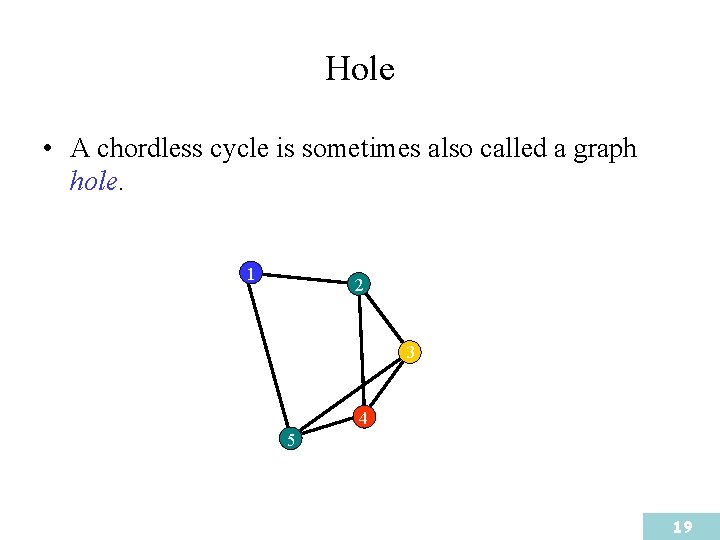
Hole • A chordless cycle is sometimes also called a graph hole. 1 2 3 4 5 19

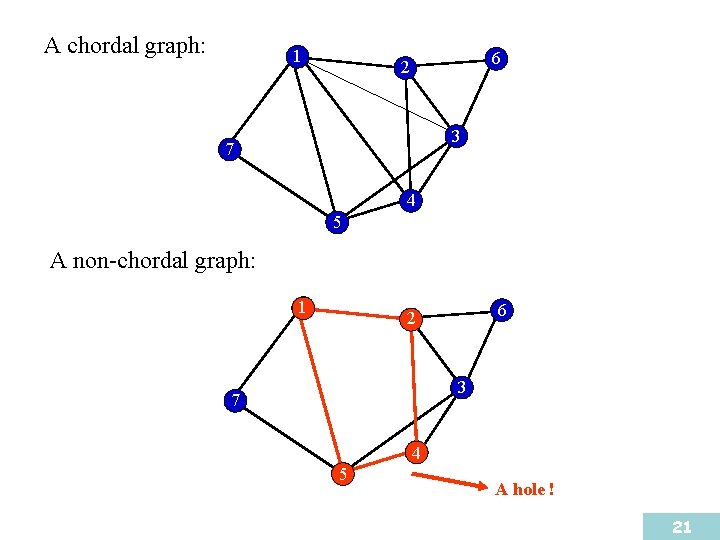
Chordal graphs • A chordal graph is a simple graph possessing no holes (chordless cycles). • That is, A graph is chordal if and only if every cycle of length greater than three has a chord. 20

A chordal graph: 1 6 2 3 7 4 5 A non-chordal graph: 1 6 2 3 7 4 5 A hole ! 21

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 22

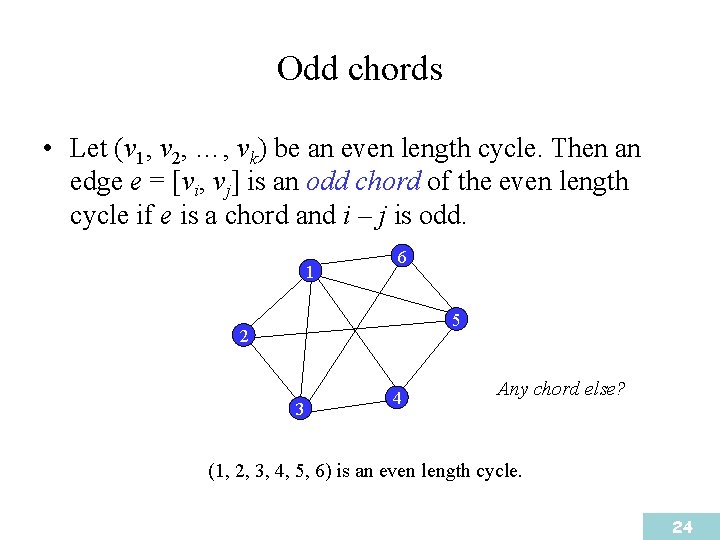
Odd chords • Let (v 1, v 2, …, vk) be an even length cycle. Then an edge e = [vi, vj] is an odd chord of the even length cycle if e is a chord and i – j is odd. 1 6 5 2 3 4 Any chord else? (1, 2, 3, 4, 5, 6) is an even length cycle. 24

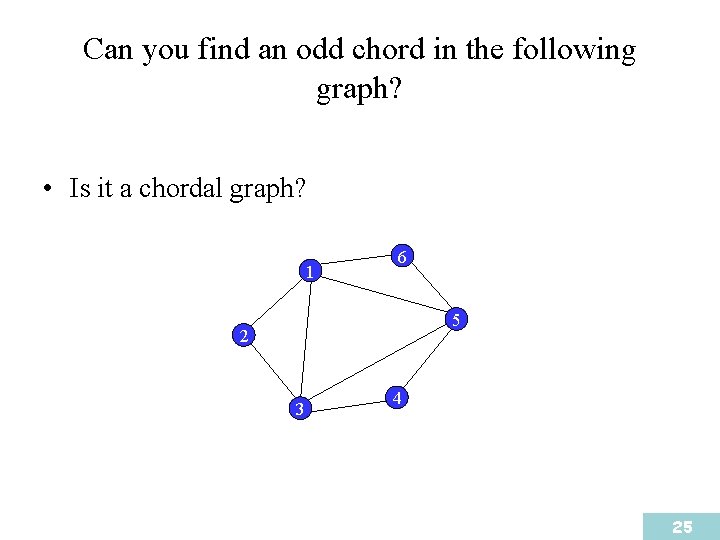
Can you find an odd chord in the following graph? • Is it a chordal graph? 1 6 5 2 3 4 25

Strongly chordal graphs • A graph is strongly chordal if it is chordal and every even length cycle of length six or more has an odd chord. Why six? • Other useful properties that characterize chordal and strongly chordal graphs are introduced in the following. 26

Simplicial vertex • N[v] = Adj(v) {v} is called the closed neighborhood of v. w v N[v] = {v, w, x, y} y x • A vertex v is called simplicial if the subgraph induced by N[v] is a clique. w v y v is simplicial x 27

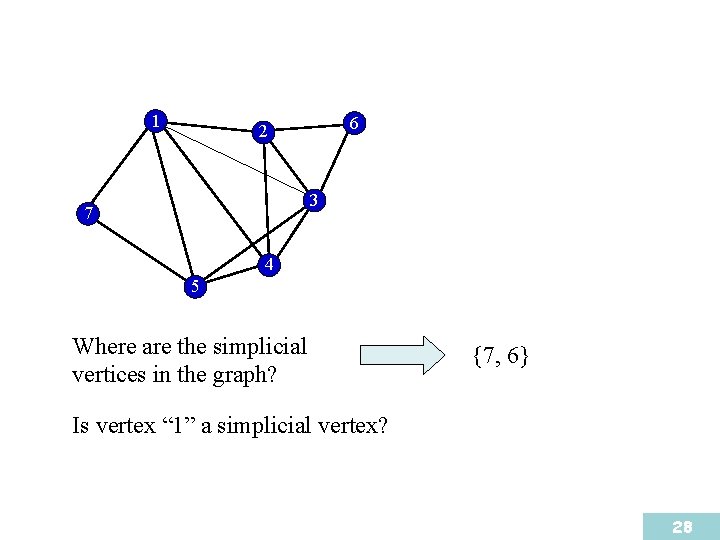
1 6 2 3 7 4 5 Where are the simplicial vertices in the graph? {7, 6} Is vertex “ 1” a simplicial vertex? 28

Perfect elimination ordering • Rose [R 70] showed that a graph G is chordal if and only if it is possible to order the vertices (v 1, v 2, …, vn) in such a way that, for each i {1, 2, …, n}, vi is a simplicial vertex of Gi = G({vi, vi+1, …, vn}), where Gi is a subgraph induced by the vertex set {vi, vi+1, …, vn}. • Such an ordering is called a perfect elimination ordering. 29

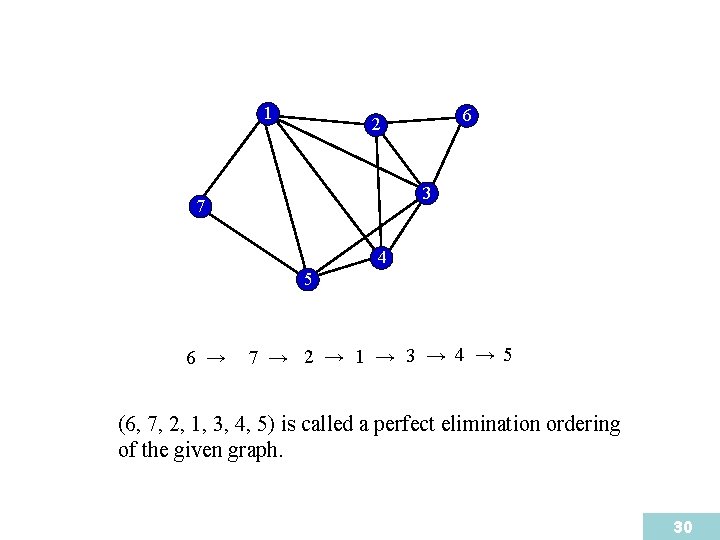
1 6 2 3 7 4 5 6 → 7 → 2 → 1 → 3 → 4 → 5 (6, 7, 2, 1, 3, 4, 5) is called a perfect elimination ordering of the given graph. 30

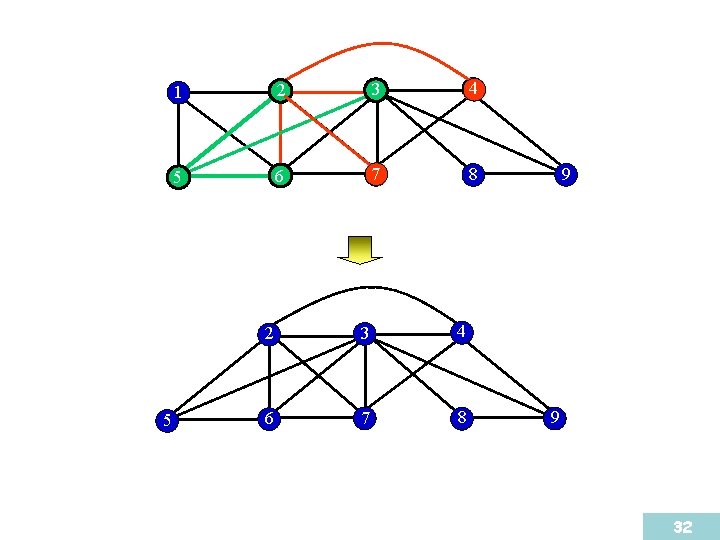
Strong elimination ordering • Let Ni[v] denote the closed neighborhood of v in Gi. • The ordering of vertices (v 1, v 2, …, vn) is called a strong elimination ordering if it is a perfect elimination ordering and, for each i < j < k, if vj and vk belong to Ni[vi] in Gi then Ni[vj] Ni[vk]. • For example, 31

5 1 2 3 4 5 6 7 8 2 3 4 6 7 8 9 9 32

Strong elimination ordering (contd. ) • In other words, for each vertex vi we not only require that vi be simplicial in Gi but in addition insist that the ordering of the vertices in Ni[vi] be consistent with the ordering of this nested family (smallest to largest). 33

Why are we concerned for the strong elimination ordering? • Farber [F 83] showed that a graph is strongly chordal if and only if it admits a strong elimination ordering. • To date (1992), the best-known time to recognize strongly chordal graphs is O(m log n). This algorithm additionally determines a strong elimination ordering. [PT 87] 34

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 35

Preliminary of the algorithm • A greedy approach is used to design this algorithm. • First, we assume that a strong elimination ordering has been constructed for the strongly chordal graph G = (V, E). • It has the property that the closed neighborhoods of the members of Ni[vi] form a nested family of sets. 37

Preliminary of the algorithm (contd. ) • The algorithm maintains + 1 disjoint sets. – Initially, these sets are empty. • The algorithm visits vertices in the reverse ordering of the strong elimination ordering. A vertex is included in a set when it is visited. 38

Preliminary of the algorithm (contd. ) • We say that a vertex v is dominated by set S if there exists a vertex u S such that u N[v]. • A vertex v is completely dominated if v is dominated by + 1 dominating sets. • Now let us see the algorithm. 39

Algorithm DP • 1. Initially, Si = for 1≤ i ≤ + 1. • 2. FOR i = n down to 1 DO • 3. Find the largest k such that vk N[vi] and vk is not completely dominated; • 4. Let Sj be a set that does not dominate vk ; • 5. Include vi in Sj, i. e. , Sj = {vi} Sj; • 6. If no such set exists, then include vi to an arbitrary set. • 7. ENDFOR 40

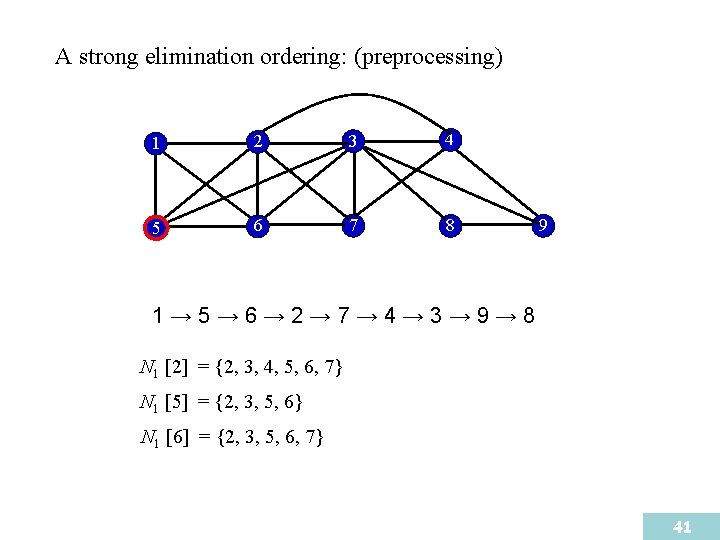
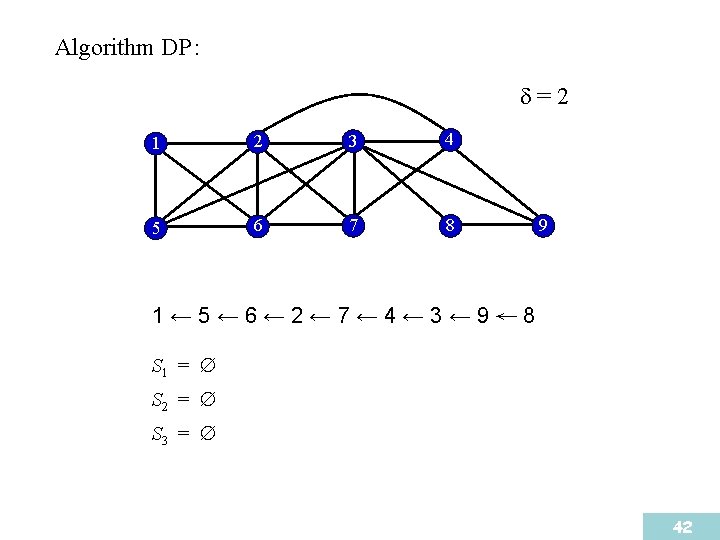
A strong elimination ordering: (preprocessing) 1 2 3 4 5 6 7 8 9 1→ 5→ 6→ 2→ 7→ 4→ 3→ 9→ 8 N 1 [2] = {2, 3, 4, 5, 6, 7} N 1 [5] = {2, 3, 5, 6} N 1 [6] = {2, 3, 5, 6, 7} 41

Algorithm DP : =2 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = S 2 = S 3 = 42

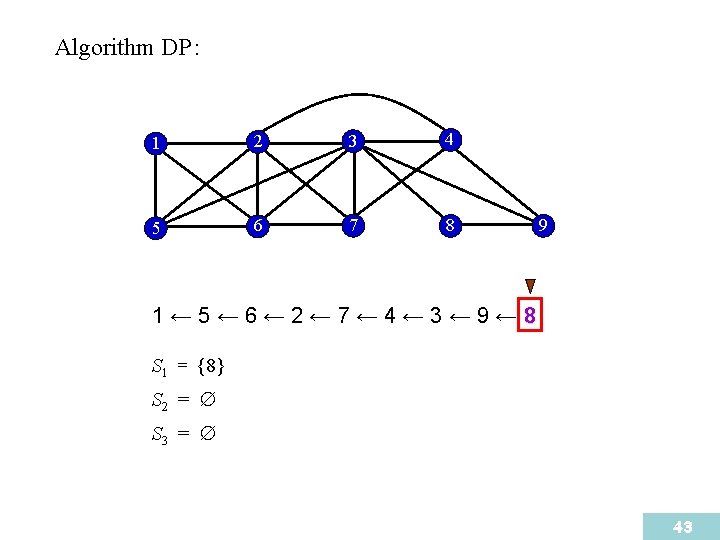
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {8} S 2 = S 3 = 43

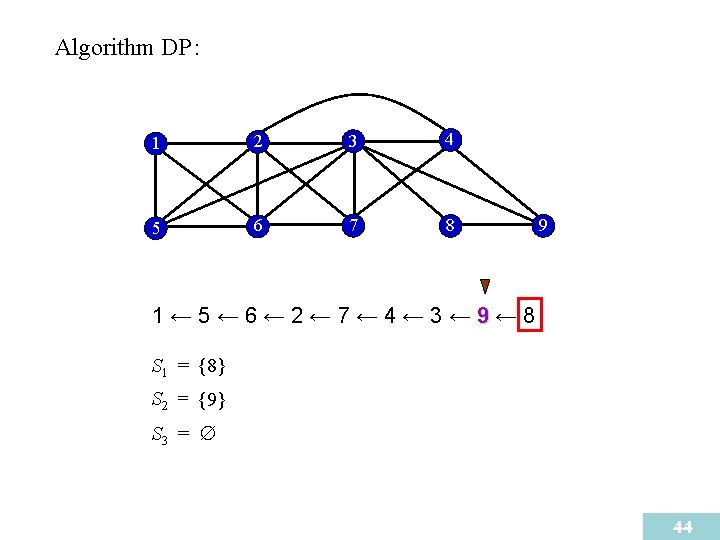
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {8} S 2 = {9} S 3 = 44

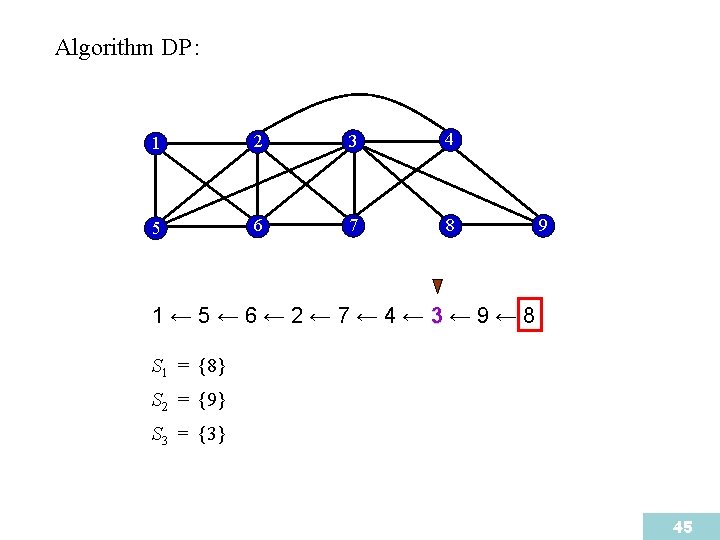
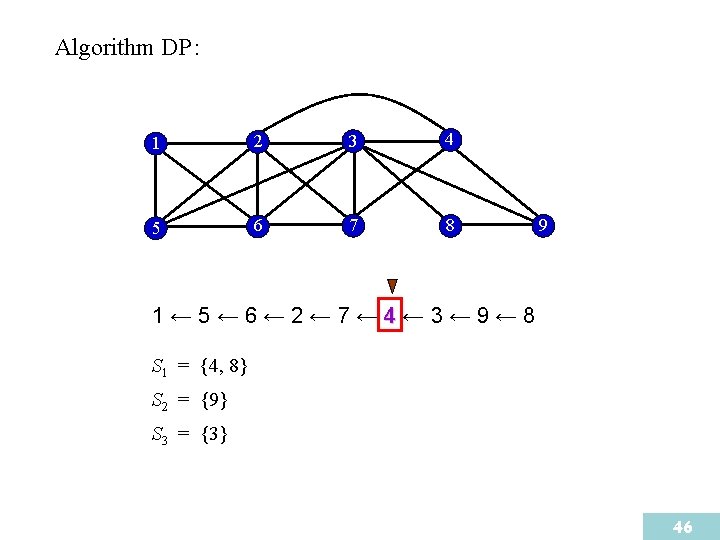
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {8} S 2 = {9} S 3 = {3} 45

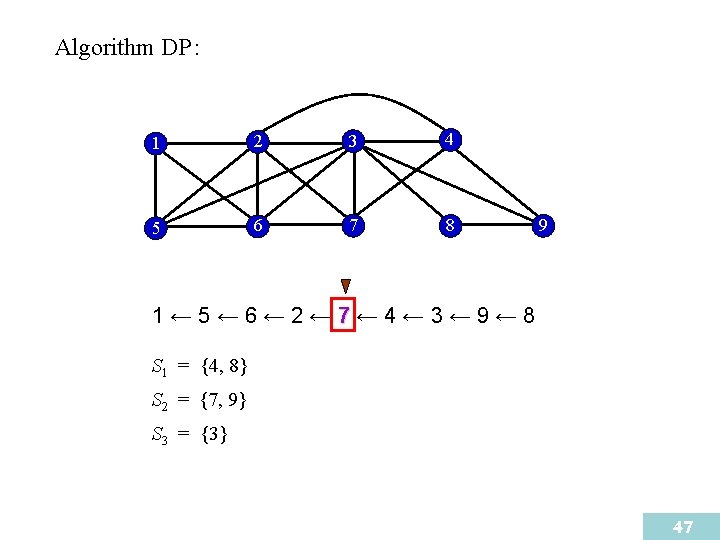
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {4, {8}8} S 2 = {9} S 3 = {3} 46

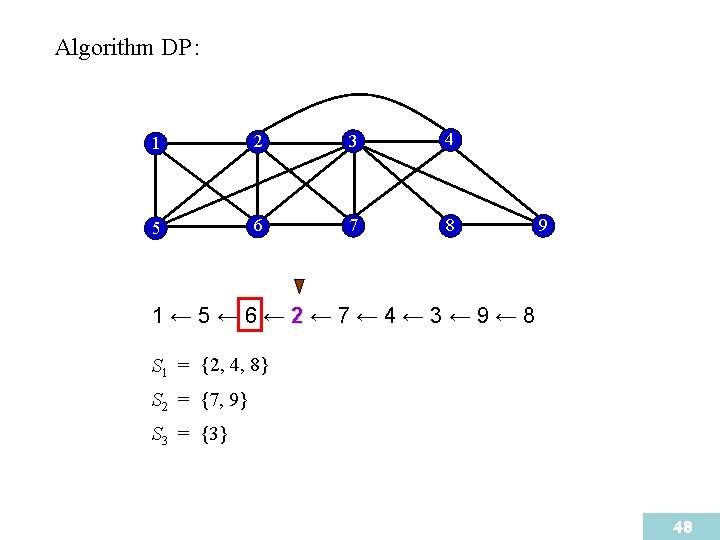
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {4, 8} S 2 = {7, {9}9} S 3 = {3} 47

Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 {2, 8} 4, 8} S 1 = {4, S 2 = {7, 9} S 3 = {3} 48

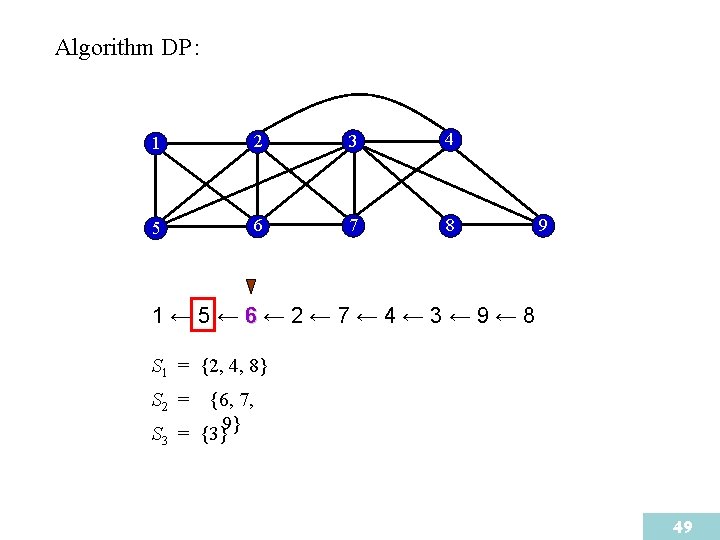
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {2, 4, 8} S 2 = {7, {6, 9} 7, S = {3}9} 3 49

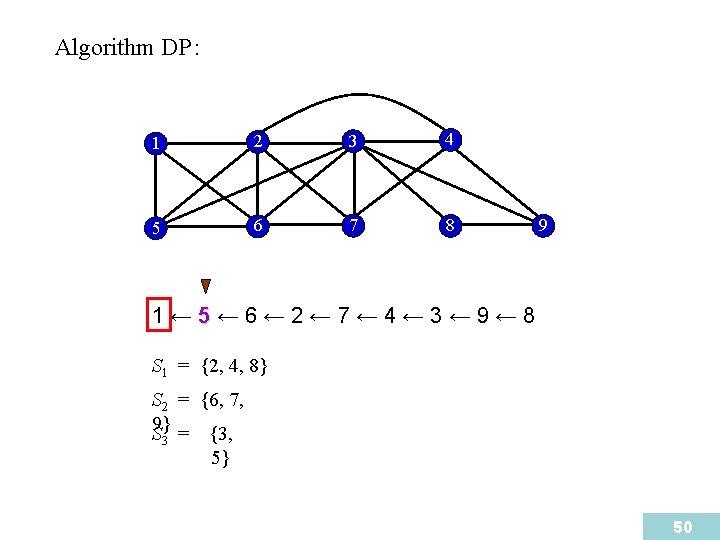
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {2, 4, 8} S 2 = {6, 7, S 9}3 = {3} {3, 5} 50

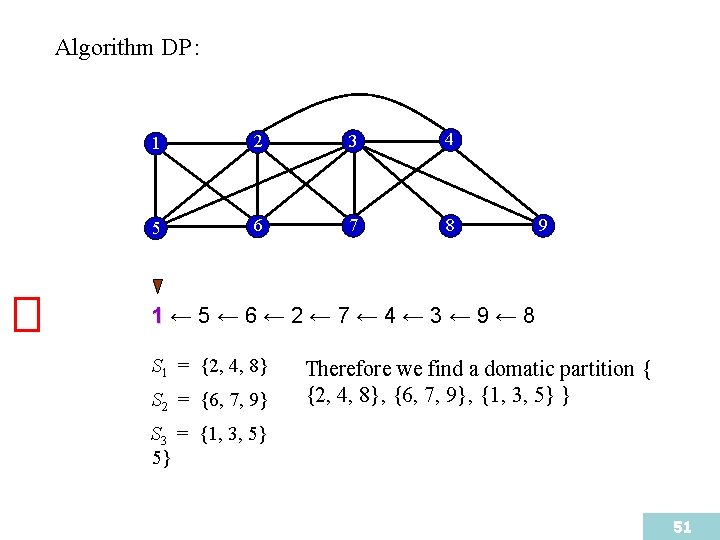
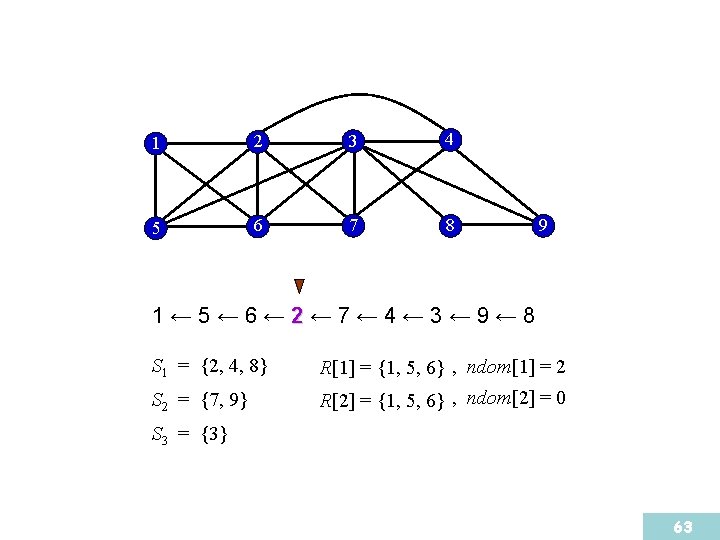
Algorithm DP : 1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {2, 4, 8} S 2 = {6, 7, 9} Therefore we find a domatic partition { {2, 4, 8}, {6, 7, 9}, {1, 3, 5} } S 3 = {1, {3, 3, 5} 5} 51

• Now let us proceed with the correctness of algorithm DP. 52

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 53

• To prove the correctness of the algorithm, we have to figure out some lemmas first. 55

Lemma 1 • Assume S {vi+1, …, vn}, vk N[vi], where 1≤ i ≤ n. If S does not dominate vk , then S does not dominate vj for all j < k and vj N[vi]. • To prove Lemma 1, we consider three cases as follows. 56

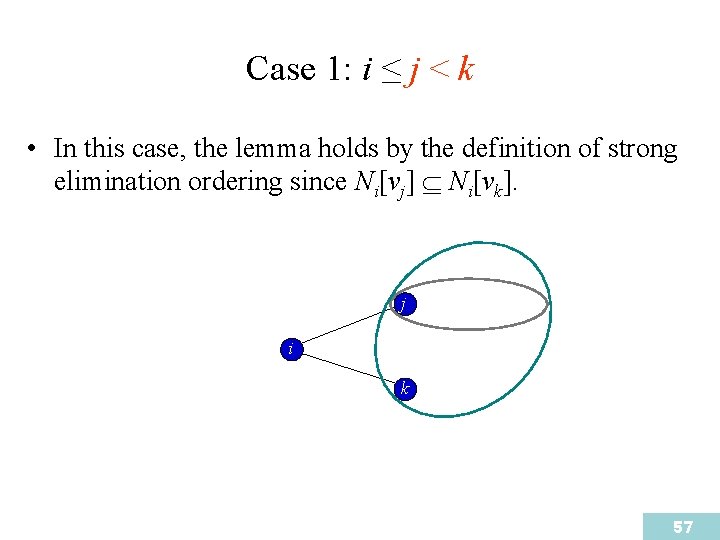
Case 1: i ≤ j < k • In this case, the lemma holds by the definition of strong elimination ordering since Ni[vj] Ni[vk]. j i k 57

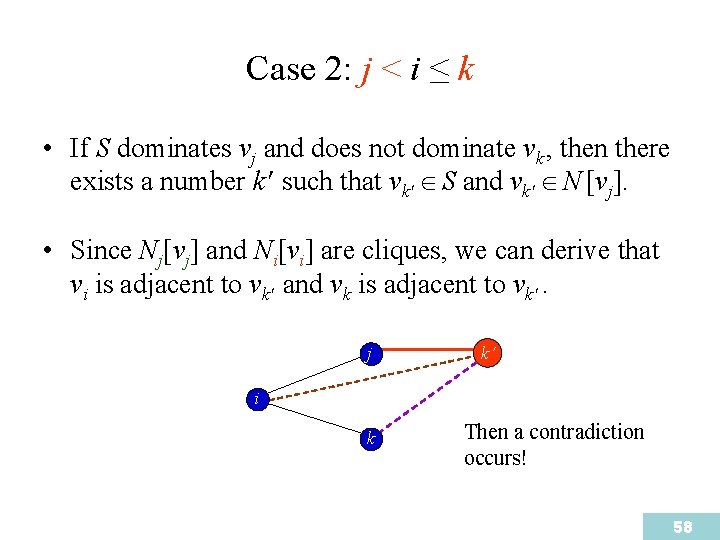
Case 2: j < i ≤ k • If S dominates vj and does not dominate vk , then there exists a number k such that vk S and vk N [vj]. • Since Nj[vj] and Ni[vi] are cliques, we can derive that vi is adjacent to vk and vk is adjacent to vk . j k i k Then a contradiction occurs! 58

Case 3: j < k < i • In this case, we also assume that S dominates vj and does not dominate vk. Then there exists a number k such that vk S and vk N [vj]. • This implies that vk is dominated by S by the property of Nj[vi] Nj[vk ]. (Notice the order of vk and S {vi+1, …, vn}) • A contradiction then occurs. – Why? j k i k 59

• Therefore, the proof of Lemma 1 is done. • Any question? 60

Corollary 1 • Assume S {vi+1, …, vn}, vk N[vi], where 1≤ i ≤ n. If S dominates vk, then S dominate vj for all j > k and vj N[vi]. • This corollary can be obtained easily from Lemma 1. 61

R[v] and ndom(v) • R[v] = {x : x N[v] and x is not in any set} – Residual neighborhood? • ndom(v) denotes the number of sets that do not dominate v during execution of Algorithm DP. 62

1 2 3 4 5 6 7 8 9 1← 5← 6← 2← 7← 4← 3← 9← 8 S 1 = {2, 4, 8} S 2 = {7, 9} R[1] = {1, 5, 6} , ndom[1] = 2 R[2] = {1, 5, 6} , ndom[2] = 0 S 3 = {3} 63

Lemma 2 • Algorithm DP maintains the following invariant: For each i {1, 2, …, n}, R[vi] ≥ ndom(vi) • We prove this lemma by induction. 64

Proof of Lemma 2 • Initially, | R[vi] | = degree(vi) + 1 and ndom(vi) = +1. – It is obvious that | R[vi] | ≥ ndom(vi) for all vi in V. • Only values of | R[vj] | and ndom(vj), where vj N[vi], may be altered when vi is included in a set. • A vertex is included in a set when it is visited by the algorithm. 65

Proof of Lemma 2 (contd. ) • The algorithm scans N[vi] to find the largest number k such that vk N[vi] and vk is not completely dominated. • We can partition N[vi] into two sets: – X = {vj : j > k and vj N[vi]} – Y = {vj : j ≤ k and vj N[vi]} 66

Proof of Lemma 2 (contd. ) X = {vj : j > k and vj N[vi]} Y = {vj : j ≤ k and vj N[vi]} • Let S be a set that does not dominate vk. • By Lemma 1, the vertices in Y are not dominated by S. • Therefore, for each vertex vj Y, both values of | R[vj] | and ndom(vj) are decremented by one after vi is included in S. – Why? 67

Proof of Lemma 2 (contd. ) X = {vj : j > k and vj N[vi]} Y = {vj : j ≤ k and vj N[vi]} • By Corollary 1, the vertices in X are all completely dominated, i. e. , ndom(vj) = 0. • Thus the invariant is maintained. – Notice that if no such vk exists, that is, all vertices in N[vi] are completely dominated, then ndom(vj) = 0, where vj N[vi]. Thus vi can be included in any set and the invariant still holds. 68

Theorem 1 • Algorithm DP correctly partitions a strongly chordal graph into + 1 disjoint dominating sets. • Proof: – Upon termination, | R[vi] | = 0 for each i {1, 2, …, n}. – By Lemma 2, | R[vi] | ≥ ndom(vi), thus ndom(vi) = 0 for all vi’s in V. – That is, all vi’s in V are dominated by all +1 dominating sets. 69

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 70

Theorem 2 • Algorithm DP is linear. • The proof is listed as follows. 71

Proof of Theorem 2 • In practical implementation, each vertex vi is associated with a variable ndom(i) and an array Li of size +1. • Initially, ndom(i) = +1 and the values of entries in Li are all zero. • If vi is dominated by Sj, then Li( j ) = 1. 72

Proof of Theorem 2 (contd. ) • Thus, for each vertex vi we can take O(di) time to determine vk , where di is the degree of vi and vk N[vi] is not completely dominated. • Then we take O( +1) time to decide in which set vi should be included. By checking Lk • Finally for each vj N[vi], we take O(1) time to update ndom(i) and Lj. O (1 di) 73

Proof of Theorem 2 (contd. ) • Therefore, the algorithm takes time of 74

Theorem 3 (Concluding theorem) • Given the strong elimination ordering of a strongly chordal graph G, we can find a domatic partition of G in linear time. 75

Outline • • Introduction Strongly Chordal Graphs Algorithm Correctness Complexity Conclusions References 76

Conclusions • We have learned the following knowledge: – Chordal graphs, strongly chordal graphs – Perfect elimination ordering and strong elimination ordering – Greedy algorithm DP 77

Mutual encouragements • Encouraging sentences • Exercise more. • Three states of our lives 78

• Think hard, not work hard. – Professor R. C. T. Lee • Think hard and work smartly. – Professor M. S. Chang • 件件 作反應自我，凡經我手必為佳作。 – Dr. D. T. Lee 79

Thank you.

References • [B 88] On the domatic number of interval graphs, A. A. Bertossi, Information Processing Letters, 28 (1988), pp. 275 -280. • [B 85] Dominating sets and domatic number of circular arc graphs, M. A. Bonuccelli, Discrete Applied Mathematics, 12 (1985), pp. 203 -213. • [BJ 82] Dominating sets in chordal graphs, K. S. Booth and J. H. Johnson, SIAM Journal on Computing, 11 (1982), pp. 191 -199. • [CH 77] Towards a theory of domination in graphs, E. J. Cockayne and S. T. Hedetniemi, Networks, 7 (1977), pp. 247 -161. • [F 83] Applications of l. p. duality to problems involving independence and domination, M. Farber, Ph. D. Thesis, Rutgers University, New Brunswick, NJ, 1982. • [F 84] Domination, independent domination, and duality in strongly chordal graphs, M. Farber, Discrete Applied Mathematics, 7 (1984), pp. 115 -130. • [GJ 79] Computers and Intractability: A Guide to the Theory of NPCompleteness, M. R. Garey and D. S. Johnson, Freeman, San Francisco, 1979.

• [G 80] Algorithm Graph Theory and Perfect Graphs (Academic Press, New York, 1980), M. C. Golumbic. • [LHC 90] The Domatic Number Problem in Interval Graphs, T. L. Lu, P. H. Ho and G. J. Chang, SIAM Journal on Discrete Mathematics, 3 (1990), pp. 531 -536. • [PT 87] Three Partition Refinement Algorithms, R. Paige and R. E. Tarjan, SIAM Journal on Computing, 16 (1987), pp. 973 -989. • [PC 91] A New Approach for Domatic Number Problem on Interval Graphs, S. L. Peng and M. S. Chang, Proceedings of National Computer Symposium, 1991, Taipei, Republic of China, pp. 236 -241. • [R 70] Triangulated Graphs and the Elimination Process, D. J. Rose, J. Math. Anal. Appl. , 32 (1970), pp. 597 -609. • [RR 89] Linear Algorithm for Domatic Number Problem on Interval Graphs, Information Processing Letters, 33 (1989), pp. 29 -33.