A Simple Greedy Algorithm for Link Scheduling with







- Slides: 19

A Simple Greedy Algorithm for Link Scheduling with the Physical Interference Model Dejun Yang (Arizona State University) Xi Fang (Arizona State University) Nan Li (Carnegie Mellon University) Guoliang Xue (Arizona State University)

Presentation Outline q Introduction q Related Work q System Model and Problem Definition q Our Greedy Algorithm q Simulation Results q Conclusion 2 of 18

Introduction 3 of 18

Related Work Link Scheduling Dr. Nelson Dr. Blough Dr. Wattenhofer Max-Cut Dr. Sahni 4 of 18

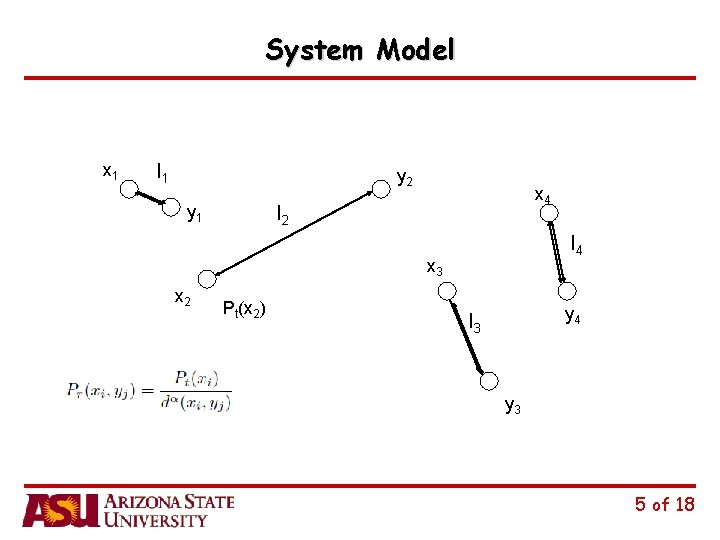
System Model x 1 l 1 y 2 x 4 l 2 y 1 l 4 x 3 x 2 Pt(x 2) y 4 l 3 y 3 5 of 18

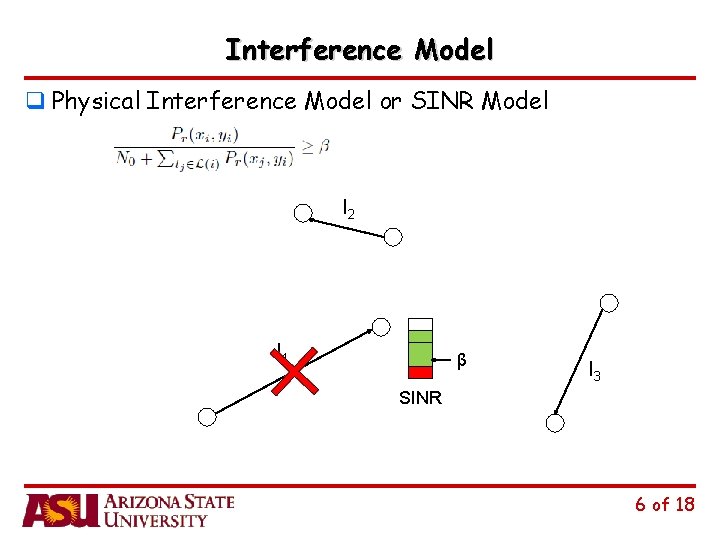
Interference Model q Physical Interference Model or SINR Model l 2 l 1 β l 3 SINR 6 of 18

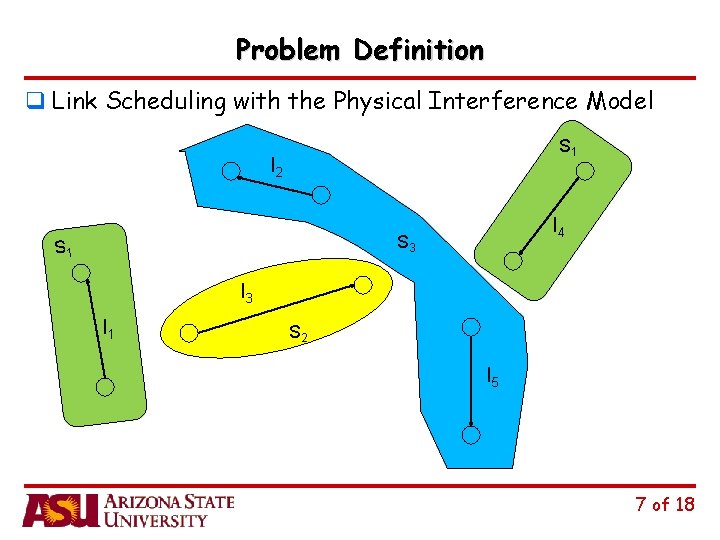
Problem Definition q Link Scheduling with the Physical Interference Model S 1 l 2 l 4 S 3 S 1 l 3 l 1 S 2 l 5 7 of 18

Current Results Our Approximation algorithm has a factor of O(g(L)). Our greedy heuristic algorithm has the best performance so far. 8 of 18

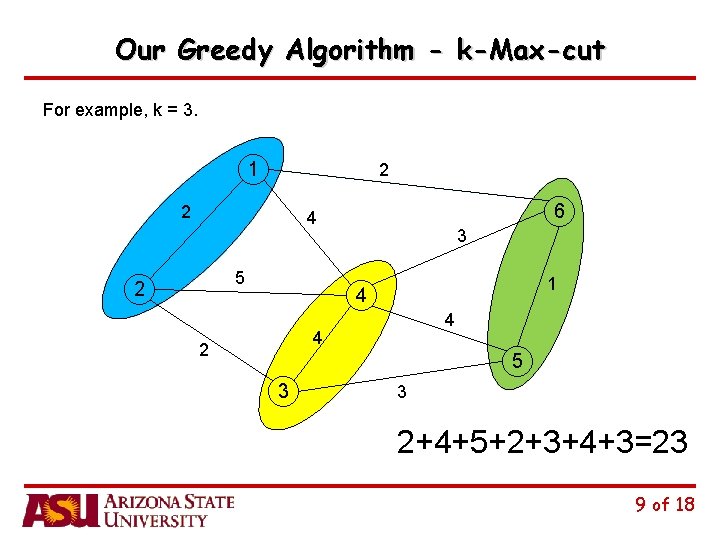
Our Greedy Algorithm - k-Max-cut For example, k = 3. 1 2 2 6 4 5 2 3 1 4 4 4 2 5 3 3 2+4+5+2+3+4+3=23 9 of 18

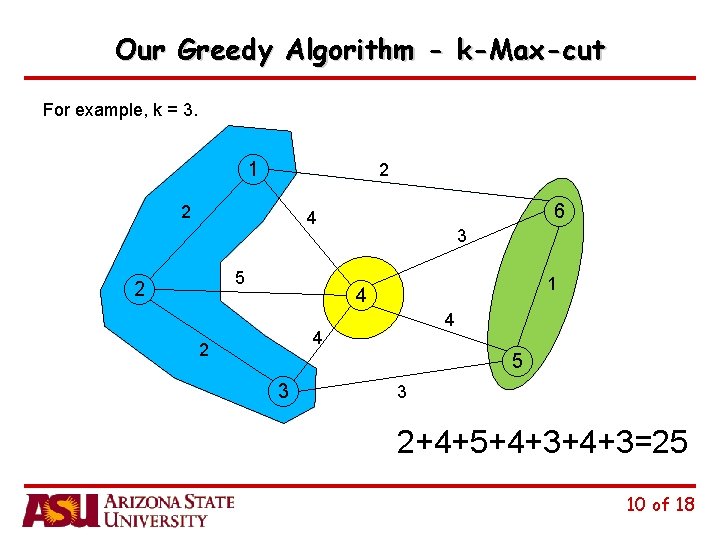
Our Greedy Algorithm - k-Max-cut For example, k = 3. 1 2 2 6 4 5 2 3 1 4 4 4 2 5 3 3 2+4+5+4+3=25 10 of 18

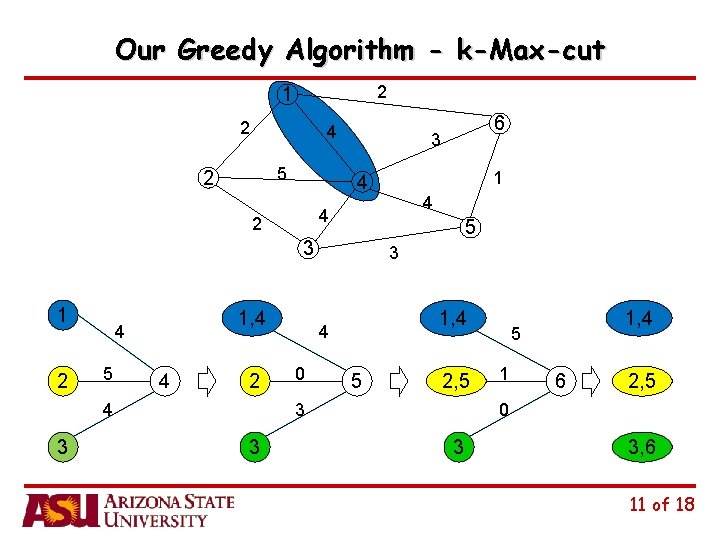
Our Greedy Algorithm - k-Max-cut 2 1 2 4 5 2 3 2 1, 4 4 5 4 2 4 3 4 4 5 3 1 1 4 2 3 1, 4 4 0 6 5 2, 5 3 3 1, 4 5 1 6 2, 5 0 3 3, 6 11 of 18

Our Greedy Algorithm - Inspiration q k-Max-Cut q Link Scheduling v. N nodes to divide v. N links to schedule v. Maximize the total weight of edges among groups v. To some extent, minimize the interference within same time slot 12/18

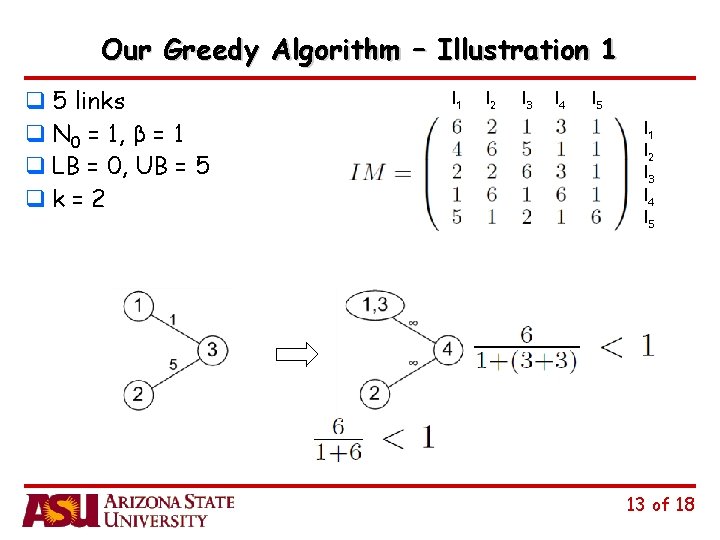
Our Greedy Algorithm – Illustration 1 q 5 links q N 0 = 1, β = 1 q LB = 0, UB = 5 qk = 2 l 1 l 2 l 3 l 4 l 5 13 of 18

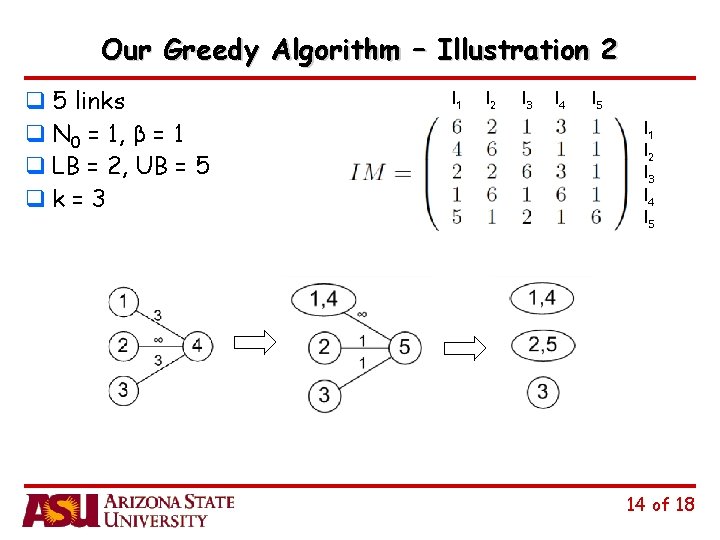
Our Greedy Algorithm – Illustration 2 q 5 links q N 0 = 1, β = 1 q LB = 2, UB = 5 qk = 3 l 1 l 2 l 3 l 4 l 5 14 of 18

Simulation Results - Settings q 1000 x 1000 square q Length of link is between 1 and 30 q N 0 = 10 -9 w q α = 2 to 4, β = 10 q Power: v Homogeneous: 200 mw v Heterogeneous: 150 mw, 200 mw and 250 mw 15 of 18

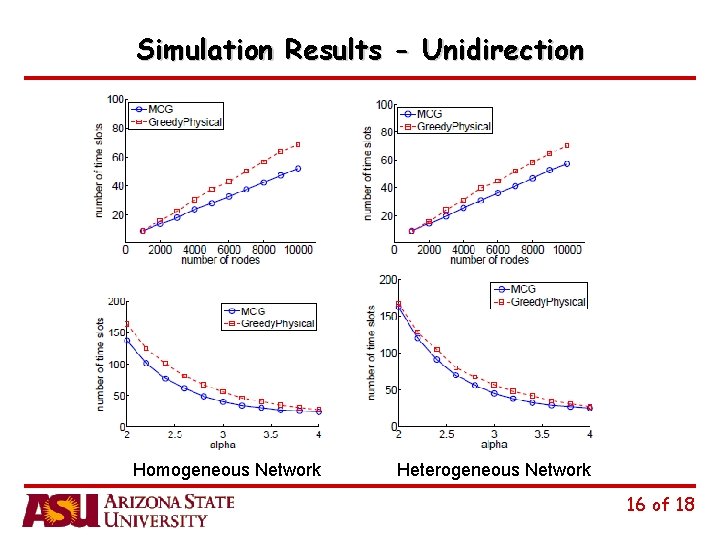
Simulation Results - Unidirection Homogeneous Network Heterogeneous Network 16 of 18

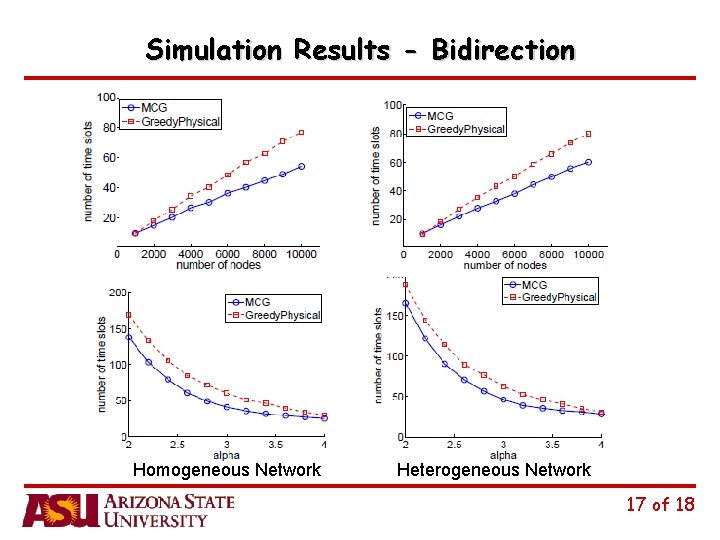
Simulation Results - Bidirection Homogeneous Network Heterogeneous Network 17 of 18

Conclusion q We proposed a polynomial O() time greedy algorithm based on k-Max-Cut. q It can be applied on both homogeneous and heterogeneous networks. q It can be applied on both unidirectional and bidirectional scenarios. q It improves the previously best result by 20%-30% in average. 18 of 18

Thank You!