A SignalProcessing Framework for Forward and Inverse Rendering

A Signal-Processing Framework for Forward and Inverse Rendering Ravi Ramamoorthi Stanford University Columbia University: Feb 11, 2002

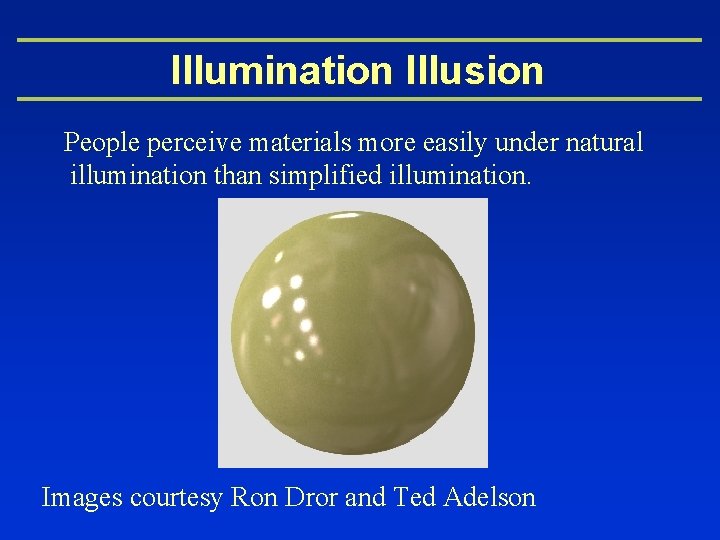
Illumination Illusion People perceive materials more easily under natural illumination than simplified illumination. Images courtesy Ron Dror and Ted Adelson

Illumination Illusion People perceive materials more easily under natural illumination than simplified illumination. Images courtesy Ron Dror and Ted Adelson

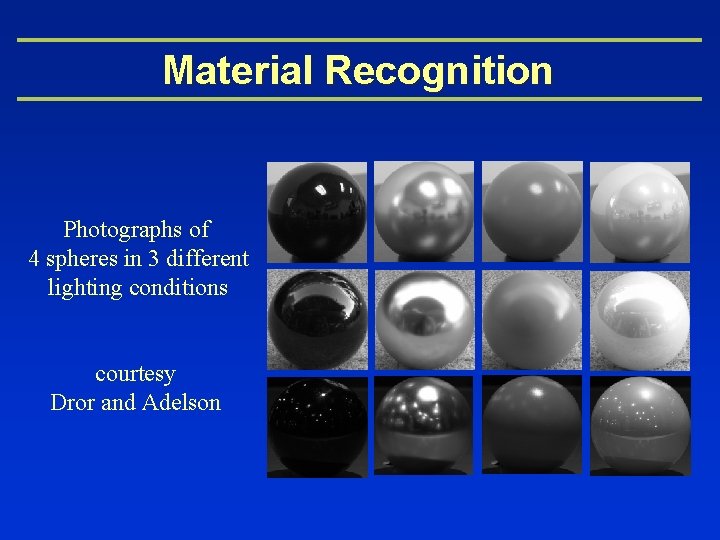
Material Recognition Photographs of 4 spheres in 3 different lighting conditions courtesy Dror and Adelson

Estimating BRDF and Lighting Photographs Inverse Rendering Algorithm BRDF Lighting Geometric model

Estimating BRDF and Lighting Photographs Forward Rendering Algorithm BRDF Rendering Lighting Geometric model

Estimating BRDF and Lighting Photographs Forward Rendering Algorithm BRDF Novel lighting Rendering Geometric model

Inverse Problems: Difficulties Surface roughness Ill-posed (ambiguous) Angular width of Light Source

Real-Time Rendering Interactive rendering with natural lighting, physical BRDFs

Motivation Understand nature of reflection and illumination Applications in computer graphics • Real-time forward rendering • Inverse rendering

Contributions of Thesis 1. Formalize reflection as convolution 2. Signal-processing framework 3. Practical forward and inverse algorithms

Outline • Motivation • Reflection as Convolution • Preliminaries, assumptions • Reflection equation, Fourier analysis (2 D) • Spherical Harmonic Analysis (3 D) • Signal-Processing Framework • Applications • Summary and Implications

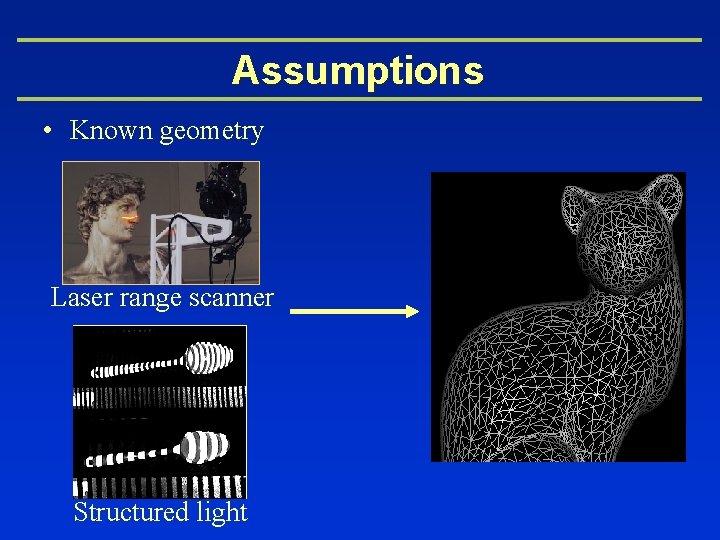
Assumptions • Known geometry Laser range scanner Structured light

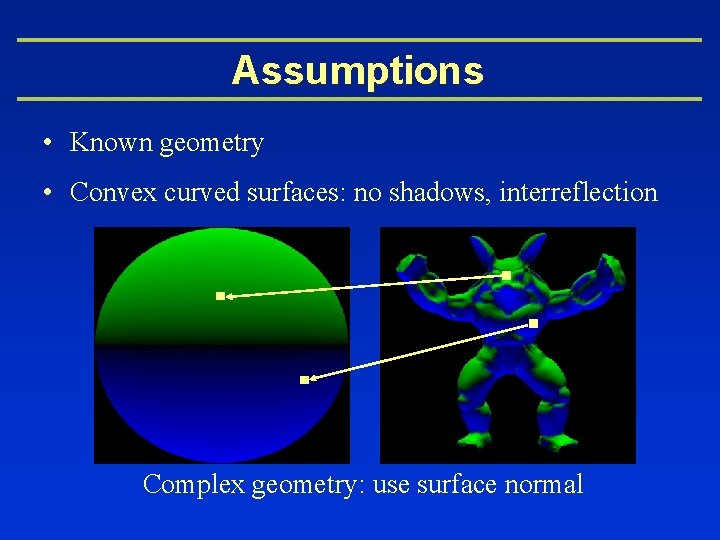
Assumptions • Known geometry • Convex curved surfaces: no shadows, interreflection Complex geometry: use surface normal

Assumptions • Known geometry • Convex curved surfaces: no shadows, interreflection • Distant illumination Photograph of mirror sphere Illumination: Grace Cathedral courtesy Paul Debevec

Assumptions • Known geometry • Convex curved surfaces: no shadows, interreflection • Distant illumination • Homogeneous isotropic materials Isotropic Anisotropic

Assumptions • Known geometry • Convex curved surfaces: no shadows, interreflection • Distant illumination • Homogeneous isotropic materials Later, practical algorithms: relax some assumptions

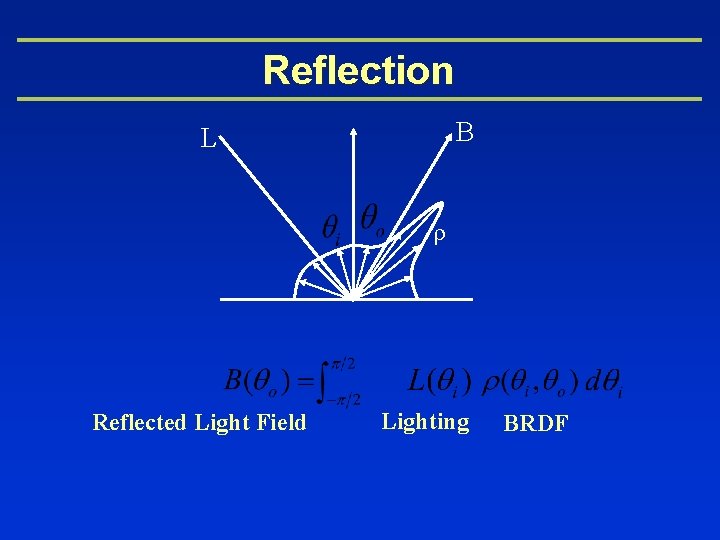
Reflection B L Reflected Light Field Lighting BRDF

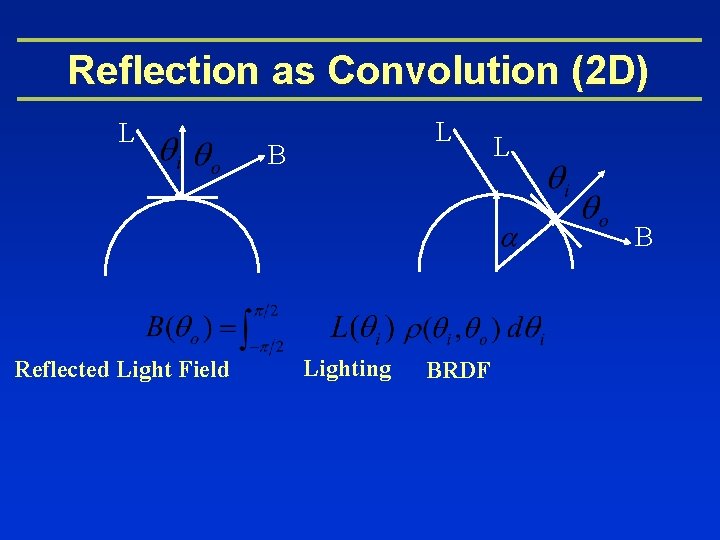
Reflection as Convolution (2 D) L L B Reflected Light Field Lighting BRDF

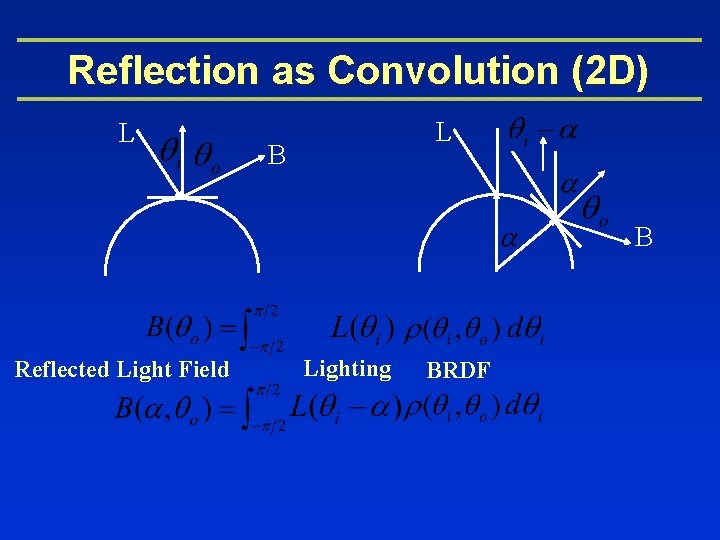
Reflection as Convolution (2 D) L L B B Reflected Light Field Lighting BRDF

Reflection as Convolution (2 D) L B

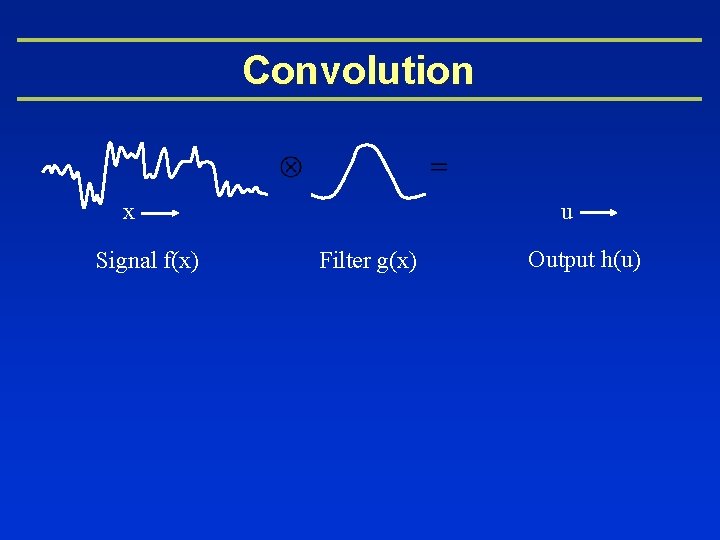
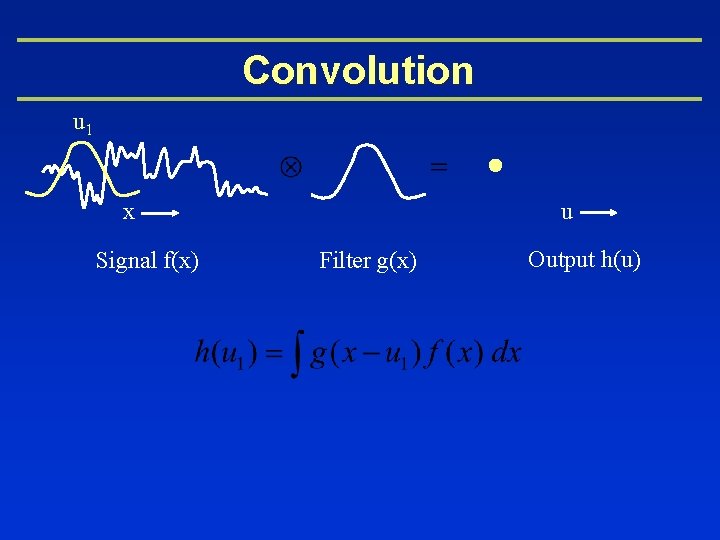
Convolution u x Signal f(x) Filter g(x) Output h(u)

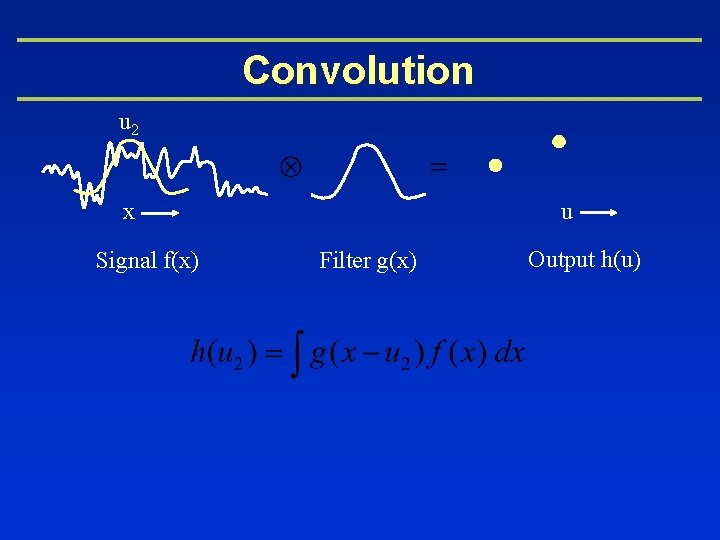
Convolution u 1 u x Signal f(x) Filter g(x) Output h(u)

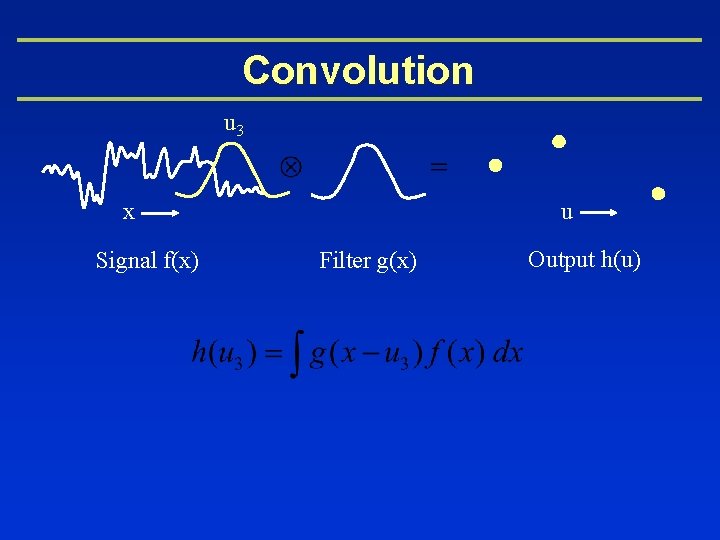
Convolution u 2 u x Signal f(x) Filter g(x) Output h(u)

Convolution u 3 u x Signal f(x) Filter g(x) Output h(u)

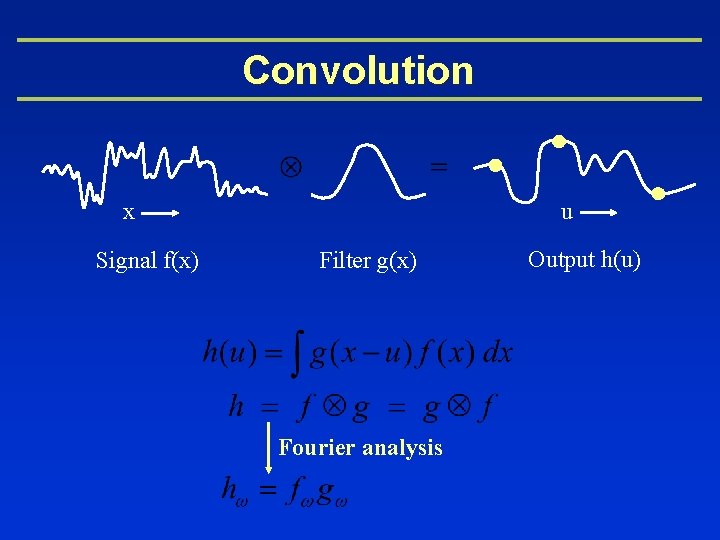
Convolution u x Signal f(x) Filter g(x) Fourier analysis Output h(u)

Reflection as Convolution (2 D) L B Spatial: integral Fourier analysis Frequency: product R. Ramamoorthi and P. Hanrahan “Analysis of Planar Light Fields from Homogeneous Convex Curved Surfaces under Distant Illumination” SPIE Photonics West 2001: Human Vision and Electronic Imaging VI pp 195 -208

Related Work • Qualitative observation of reflection as convolution: Miller & Hoffman 84, Greene 86, Cabral et al. 87, 99 • Reflection as frequency-space operator: D’Zmura 91 • Lambertian reflection is convolution: Basri Jacobs 01 Our Contributions • Explicitly derive frequency-space convolution formula • Formal quantitative analysis in general 3 D case

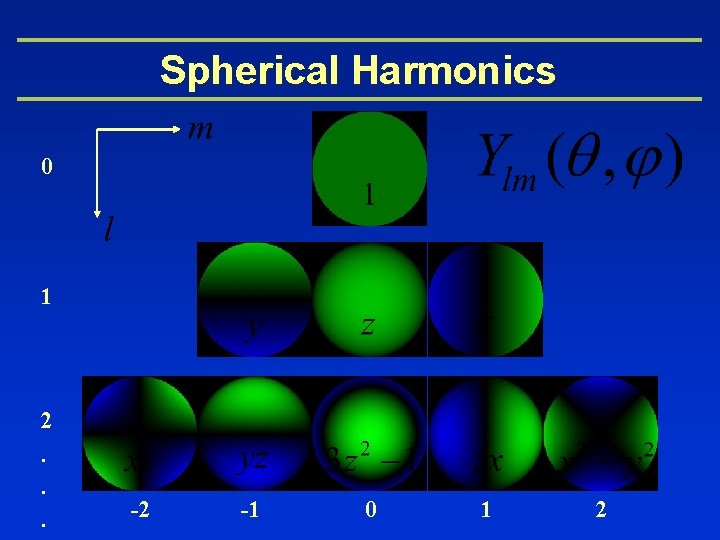
Spherical Harmonics 0 1 2. . . -2 -1 0 1 2

Spherical Harmonic Analysis 2 D: 3 D:

Outline • Motivation • Reflection as Convolution • Signal-Processing Framework • Insights, examples • Well-posedness of inverse problems • Applications • Summary and Implications

Insights: Signal Processing Signal processing framework for reflection • Light is the signal • BRDF is the filter • Reflection on a curved surface is convolution

Insights: Signal Processing Signal processing framework for reflection • Light is the signal • BRDF is the filter • Reflection on a curved surface is convolution Filter is Delta function : Output = Signal Mirror BRDF : Image = Lighting [Miller and Hoffman 84] Image courtesy Paul Debevec

Insights: Signal Processing Signal processing framework for reflection • Light is the signal • BRDF is the filter • Reflection on a curved surface is convolution Signal is Delta function : Output = Filter Point Light Source : Images = BRDF [Marschner et al. 00]

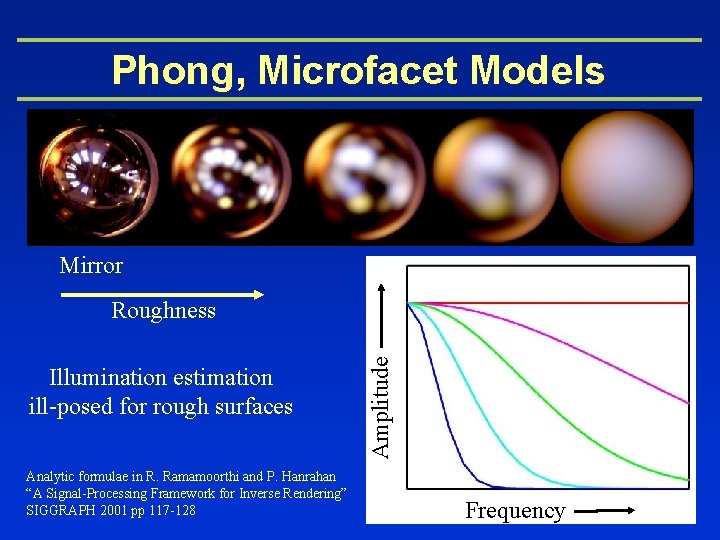
Phong, Microfacet Models Mirror Illumination estimation ill-posed for rough surfaces Analytic formulae in R. Ramamoorthi and P. Hanrahan “A Signal-Processing Framework for Inverse Rendering” SIGGRAPH 2001 pp 117 -128 Amplitude Roughness Frequency

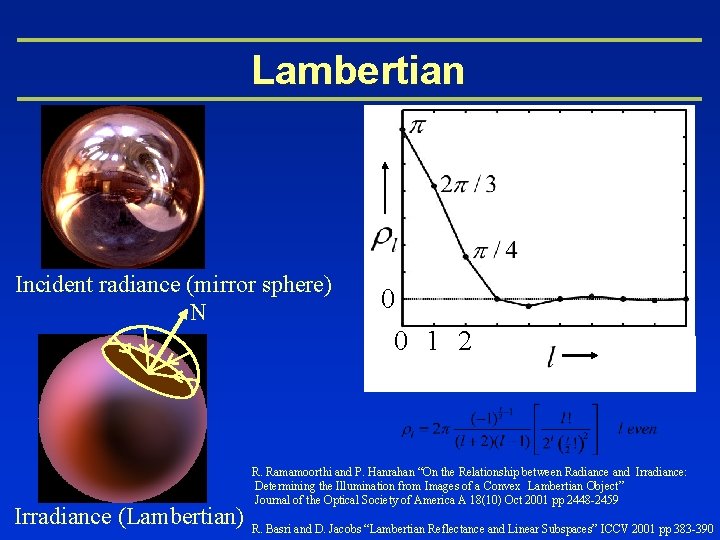
Lambertian Incident radiance (mirror sphere) N Irradiance (Lambertian) 0 0 1 2 R. Ramamoorthi and P. Hanrahan “On the Relationship between Radiance and Irradiance: Determining the Illumination from Images of a Convex Lambertian Object” Journal of the Optical Society of America A 18(10) Oct 2001 pp 2448 -2459 R. Basri and D. Jacobs “Lambertian Reflectance and Linear Subspaces” ICCV 2001 pp 383 -390

Inverse Lighting Given: B, ρ find L Well-posed unless denominator vanishes • BRDF should contain high frequencies : Sharp highlights • Diffuse reflectors low pass filters: Inverse lighting ill-posed

Inverse BRDF Given: B, L find ρ Well-posed unless Llm vanishes • Lighting should have sharp features (point sources, edges) • BRDF estimation ill-conditioned for soft lighting Directional Area source Same BRDF

Factoring the Light Field Given: B find L and ρ 4 D 2 D 3 D More knowns (4 D) than unknowns (2 D/3 D) Light Field can be factored • Up to global scale factor • Assumes reciprocity of BRDF • Can be ill-conditioned • Analytic formula derived

Outline • Motivation • Reflection as Convolution • Signal-Processing Framework • Applications • Forward rendering (convolution) • Inverse rendering (deconvolution) • Summary and Implications

Computing Irradiance • Classically, hemispherical integral for each pixel Incident Radiance • Lambertian surface is like low pass filter • Frequency-space analysis Irradiance

9 Parameter Approximation Order 0 1 term (constant) Exact image RMS error = 25 % 0 1 2 -2 -1 0 1 2

9 Parameter Approximation Order 1 4 terms (linear) Exact image RMS Error = 8% 0 1 2 -2 -1 0 1 2

9 Parameter Approximation Order 2 9 terms (quadratic) Exact image RMS Error = 1% For any illumination, average error < 2% [Basri Jacobs 01] 0 1 2 -2 -1 0 1 2

Comparison Incident illumination 300 x 300 Irradiance map Texture: 256 x 256 Hemispherical Integration 2 Hrs Irradiance map Texture: 256 x 256 Spherical Harmonic Coefficients 1 sec

Video R. Ramamoorthi and P. Hanrahan “An Efficient Representation for Irradiance Environment Maps” SIGGRAPH 2001 pp 497 -500 R. Ramamoorthi and P. Hanrahan “Frequency Space Environment Map Rendering” submitted

Video

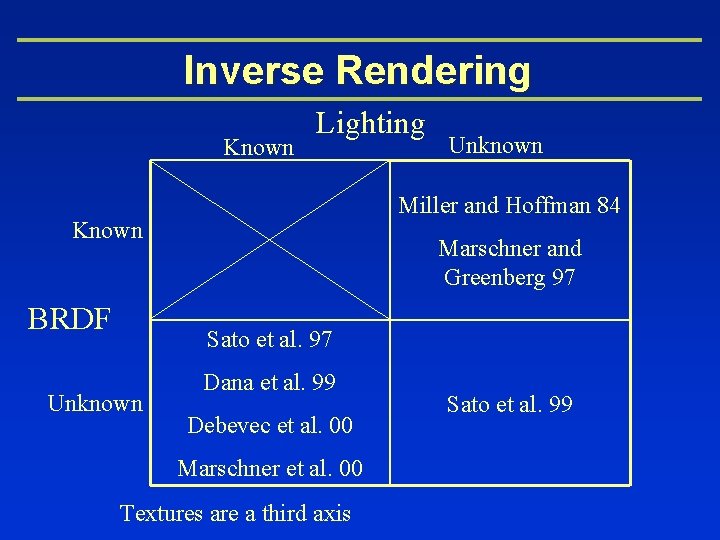
Inverse Rendering Known Lighting Miller and Hoffman 84 Known BRDF Unknown Marschner and Greenberg 97 Sato et al. 97 Unknown Dana et al. 99 Debevec et al. 00 Marschner et al. 00 Textures are a third axis Sato et al. 99

Contributions • Complex illumination • Factorization of BRDF, lighting (find both) • New representations and algorithms • Formal study of inverse problems (well-posed? )

Complications • Incomplete sparse data (few photographs) • Concavities: Self Shadowing • Spatially varying BRDFs

Complications Challenge: Incomplete sparse data (few photographs) Difficult to compute frequency spectra Solution: • Use parametric BRDF model • Dual angular and frequency space representation

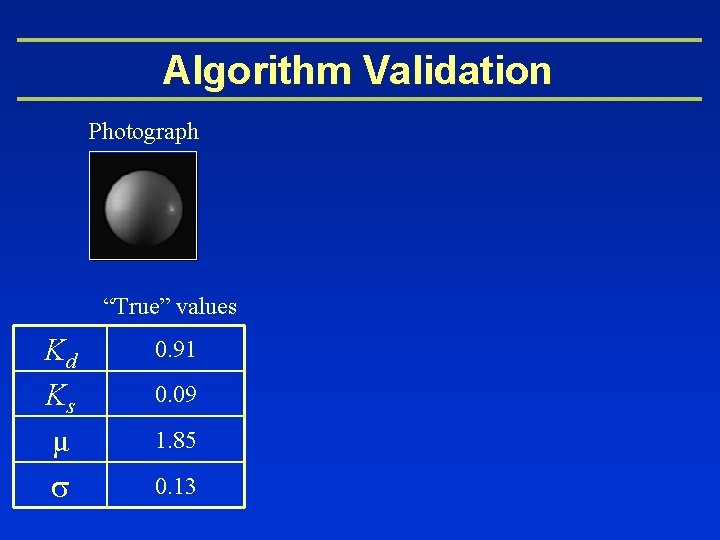
Algorithm Validation Photograph “True” values Kd Ks μ s 0. 91 0. 09 1. 85 0. 13

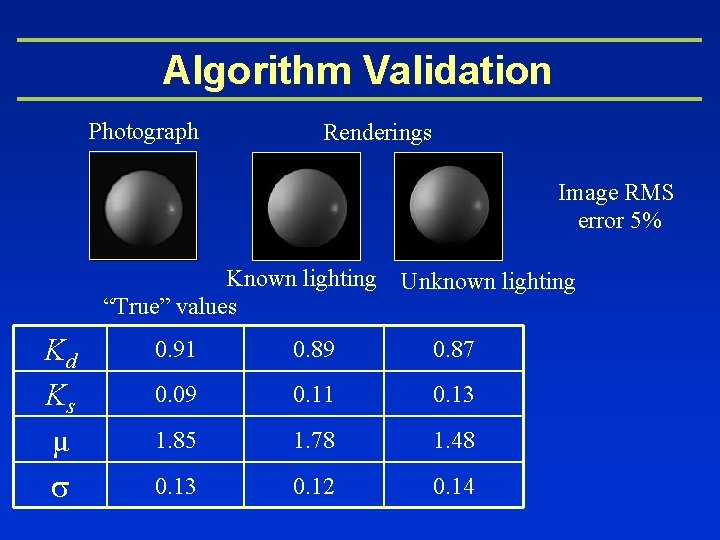
Algorithm Validation Photograph Renderings Image RMS error 5% Known lighting Unknown lighting “True” values Kd Ks μ s 0. 91 0. 89 0. 87 0. 09 0. 11 0. 13 1. 85 1. 78 1. 48 0. 13 0. 12 0. 14

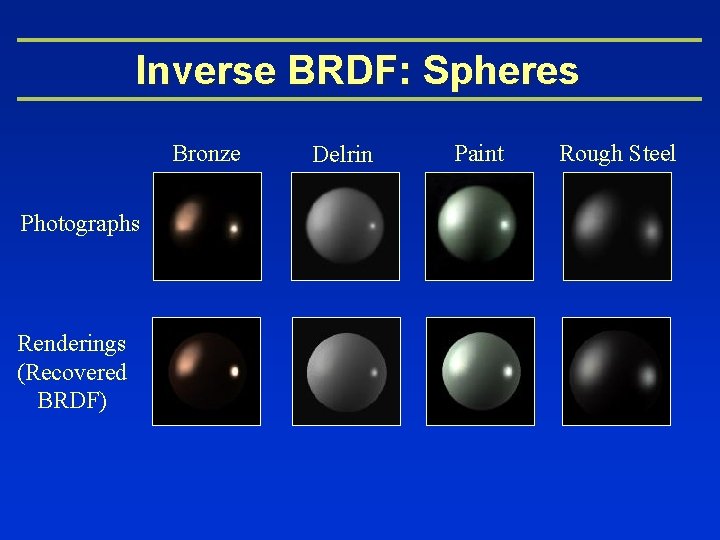
Inverse BRDF: Spheres Bronze Photographs Renderings (Recovered BRDF) Delrin Paint Rough Steel

Complications Challenge: Complex geometry with concavities Self shadowing Solution: • Use associativity of convolution • Blur lighting, treat specular BRDF term as mirror • Single ray for shadowing, easy in ray tracer

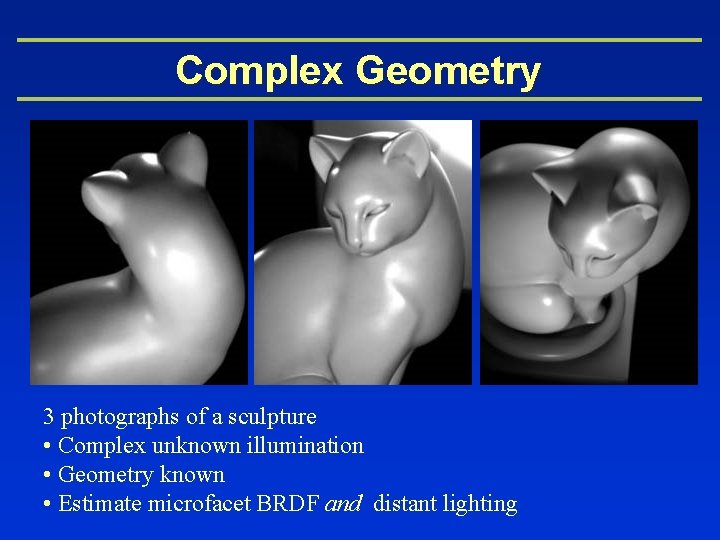
Complex Geometry 3 photographs of a sculpture • Complex unknown illumination • Geometry known • Estimate microfacet BRDF and distant lighting

Comparison Photograph Rendering

New View, Lighting Photograph Rendering

Complications Challenge: Spatially varying BRDFs Solution: • Use textures to modulate BRDF parameters

Textured Objects Photograph Rendering

Summary • Reflection as convolution • Frequency-space analysis gives many insights • Practical forward and inverse algorithms • Signal-Processing: A useful paradigm forward and inverse rendering in graphics and vision

Implications and Future Work Duality between forward and inverse problems: Ill -posed inverse problem fast forward algorithm Example: Inverse lighting from Lambertian surface ill-posed computing irradiance is fast

Implications and Future Work Differential framework for reflection • Analysis on object surface • Complex illumination and BRDF

Implications and Future Work Analyzing intrinsic structure, complexity of light field: Sampling theory based on signal-processing • How many images in image-based rendering? • How many principal components in PCA?

Lighting Invariant Recognition Theory: Space of images infinite-dimensional for Lambertian [Belhumeur and Kriegman 98] Empirical: 5 D subspace enough for diffuse objects [Hallinan 94, Epstein et al. 95, BK 98, …] Images from Yale face database

Implications and Future Work Complex illumination in computer vision • Generally assume simple lighting (point source) without considering visibility (attached shadows) • Signal processing can be used to reduce effects of complex illumination (with shadows) to low-dimensional subspace • Many applications: stereo, photometric stereo, shape from shading, lighting invariant recognition etc.

Acknowledgements • Pat Hanrahan • Marc Levoy • Szymon Rusinkiewicz • Steve Marschner • Stanford graphics group • Hodgson-Reed Stanford Graduate Fellowship • NSF ITR grant #0085864: “Interacting with the Visual World”

Papers R. Ramamoorthi and P. Hanrahan “A Signal-Processing Framework for Inverse Rendering” SIGGRAPH 2001 pp 117 -128 R. Ramamoorthi and P. Hanrahan “An Efficient Representation for Irradiance Environment Maps” SIGGRAPH 2001 pp 497 -500 R. Ramamoorthi and P. Hanrahan “Frequency Space Environment Map Rendering” submitted R. Ramamoorthi and P. Hanrahan “On the Relationship between Radiance and Irradiance: Determining the Illumination from images of a Convex Lambertian Object” Journal of the Optical Society of America A 18(10) 2001 pp 2448 -2459 R. Ramamoorthi and P. Hanrahan “Analysis of Planar Light Fields from Homogeneous Convex Curved Surfaces under Distant Illumination” SPIE Photonics West 2001: Human Vision and Electronic Imaging VI pp 195 -208 R. Ramamoorthi “Analytic PCA Construction for Theoretical Analysis of Lighting Variability, Including Attached Shadows, in a Single Image of a Convex Lambertian Object” CVPR 2001 workshop on Identifying Objects across Lighting Variations pp 48 -55 ravir@graphics. stanford. edu http: //graphics. stanford. edu/~ravir

The End

Photorealistic Rendering Geometry Rendering Algorithm 70’s, 80’s: Splines 90’s: Range Data Materials/Lighting (Texture Reflectance[BRDF] Lighting) Realistic input models required Arnold Renderer: Marcos Fajardo 80’s, 90’s: Physically based

Measuring Materials, Light Measure Illumination: Mirror Sphere Illumination: Grace Cathedral courtesy Paul Debevec Measure BRDF (reflectance): Point light source

Interactive Forward Rendering Classically, rendering with natural illumination is very expensive compared to using simplified illumination Directional Source Natural Illumination

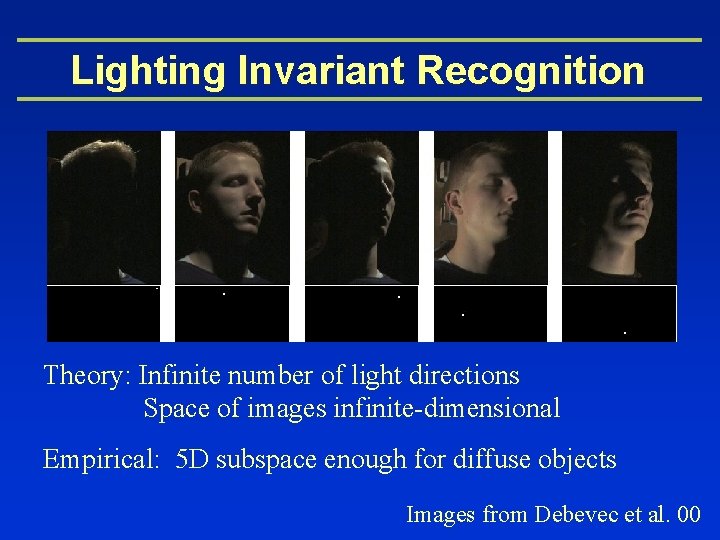
Lighting Invariant Recognition Theory: Infinite number of light directions Space of images infinite-dimensional Empirical: 5 D subspace enough for diffuse objects Images from Debevec et al. 00

Lighting Invariant Recognition Theory: Space of images infinite-dimensional for Lambertian [Belhumeur and Kriegman 98] Empirical: 5 D subspace enough for diffuse objects [Hallinan 94, Epstein et al. 95, BK 98, …]

Open Questions • Relationship between spherical harmonics, PCA • 9 D approximation > 5 D empirical subspace Key insight: Consider approximations over visible normals (upper hemisphere), not entire sphere % VAF 42% Frontal 4% 2% 33% 16% Side Above/Below Extreme side Corner Ramamoorthi CVPR IOAVL 01

Light Field in 3 D In flatland, 2 D function In three dimensions, 4 D function Plenoptic Light Field Surface Light Field

Dual Representation Diffuse BRDF: Filter width small in frequency domain Specular: Filter width small in spatial (angular) domain Practical Representation: Dual angular, frequency-space = B + Bd diffuse Frequency Bs specular Angular

Related Work • Precomputed (prefiltered) Irradiance maps [Miller and Hoffman 84, Greene 86, Cabral et al 87] • Empirical observation: Irradiance varies slowly with surface normal. Use low resolution irradiance maps Contributions • • Analytic Irradiance formula Fast computation Compact 9 parameter representation Procedural rendering with programmable shading hardware Our approach can be extended to general BRDFs

Comparison Rendering (known L) Photograph Rendering (unknown L)