A sequence is ARITHMETIC if the differences between

A sequence is ARITHMETIC if the differences between consecutive terms are the same. ex. 2, 7, 12, 17, 22, 27 5 is the common difference. an+1 = an + d a 1 is the first term d is the common diff. a 1 = 2 an+1 = an + 5

ex. 3, 5/2, 2, 3/2, 1 Is this an arithmetic sequence? Find the common difference (d). a 1 = ? an + 1 = ?

A sequence is GEOMETRIC if the ratios of consecutive terms are the same. ex. 3, 6, 12, 24, 48, 96 2 is the common ratio. an+1 = an r a 1 is the first term r is the common ratio a 1 = 3 an+1 = an 2

ex. 5, 1, 0. 2, 0. 04 Is this a geometric sequence? Find the common ratio (r). a 1 = ? an + 1 = ? Ex. a 1 = 7 d = 2 Write the first 4 terms of the sequence.

Ex. a 1 = 7 d = 2 Write the first 4 terms of the sequence. Ex. a 1 = 3 r = 4 Write the first 4 terms of the sequence. Ex. a 1 = 7 ak + 1 = -¾ ak Write the first 4 terms of the sequence.

Finding the nth term of a sequence Arithmetic: an = a 1 + ( n – 1) d n– 1 Geometric: a n = a 1 r Ex. a 1 = 15 d = 4 Find a 10 Ex. a 1 = 5 r = 3/2 Find a 8

The sum of a finite arithmetic sequence with n terms: Carl Friedrich Gauss

The sum of a finite geometric sequence with n terms: The sum of an infinite geometic sequence: If |r| < 1 What happens if n becomes infinitely large? What if |r| >1 ?

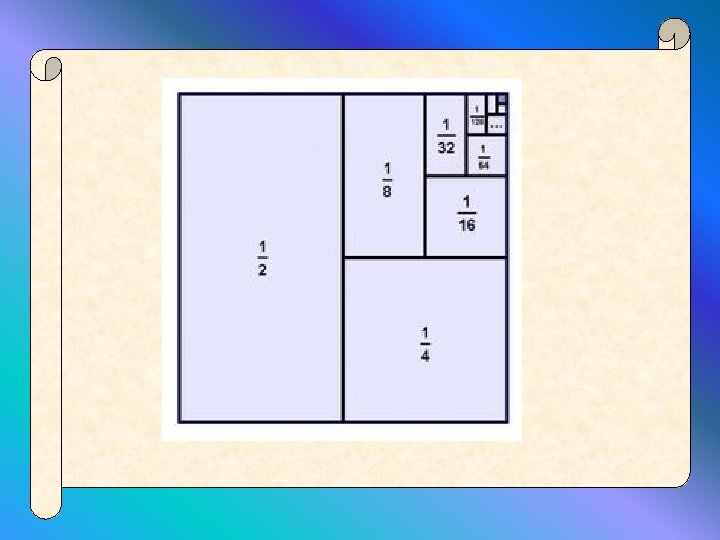
infinite sequence finite sum

ex. 1 2 3 4 8 15 22 29 This number is the arithmetic mean of 15 and 29 ex. 1 2 3 4 2 6 18 54 This number is the geometric mean of 6 and 54

How Many Grains of Rice? We are trying to find the sum of a geometric sequence with 30 terms and a common ratio of 2. A 1 pound bag has about 25, 000 grains of rice. So this amount would represent roughly 42, 950 one pound bags!