A Scientific and Statistical Analysis of Accelerated Aging

A Scientific and Statistical Analysis of Accelerated Aging for Pharmaceuticals: Accuracy and Precision of Fitting Methods Kenneth C. Waterman, Ph. D. Jon Swanson, Ph. D. Free. Think Technologies, Inc. ken. waterman@freethinktech. com 2014 1

• Accuracy in accelerated aging • Point estimates • Linear estimates • Isoconversion • Uncertainty in predictions • Isoconversion methods • Arrhenius Outline • Distributions (MC vs. extrema isoconversion) • Linear vs. non-linear • Low degradant • Conclusions ken. waterman@freethinktech. com 2014 2

Accuracy in Accelerated Aging • Statistics must be based on accurate models • Most shelf-life today determined by degradant growth not potency loss • >50% Drug products show complex kinetics: do not show linear behavior • Heterogeneous systems • Secondary degradation • Autocatalysis • Inhibitors • Diffusion controlled ken. waterman@freethinktech. com 2014 3

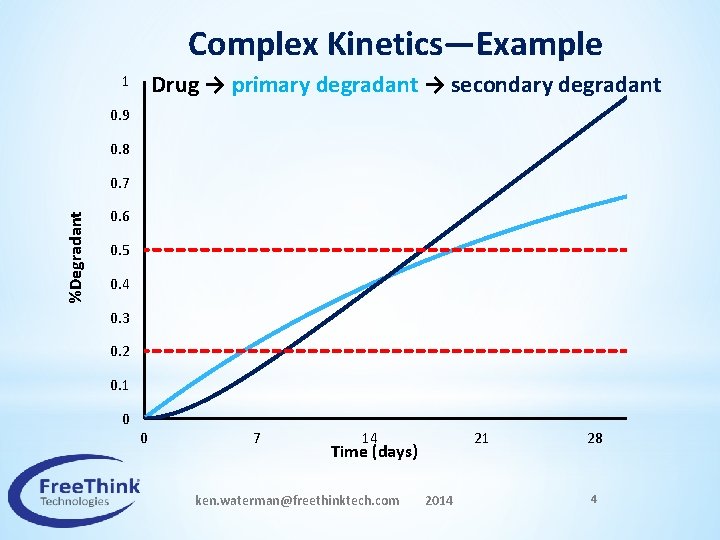
Complex Kinetics—Example Drug → primary degradant → secondary degradant 1 0. 9 0. 8 %Degradant 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 0 7 14 Time (days) ken. waterman@freethinktech. com 2014 21 28 4

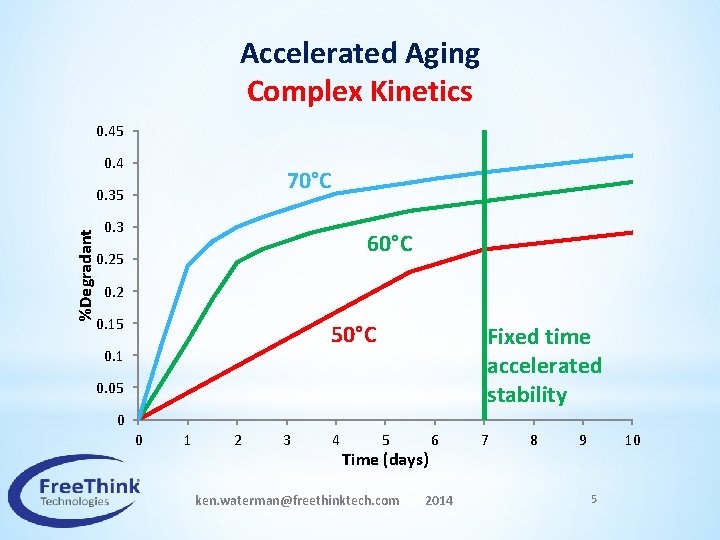
Accelerated Aging Complex Kinetics 0. 45 0. 4 70°C %Degradant 0. 35 0. 3 60°C 0. 25 0. 2 0. 15 50°C 0. 1 Fixed time accelerated stability 0. 05 0 0 1 2 3 4 5 Time (days) 6 ken. waterman@freethinktech. com 2014 7 8 9 10 5

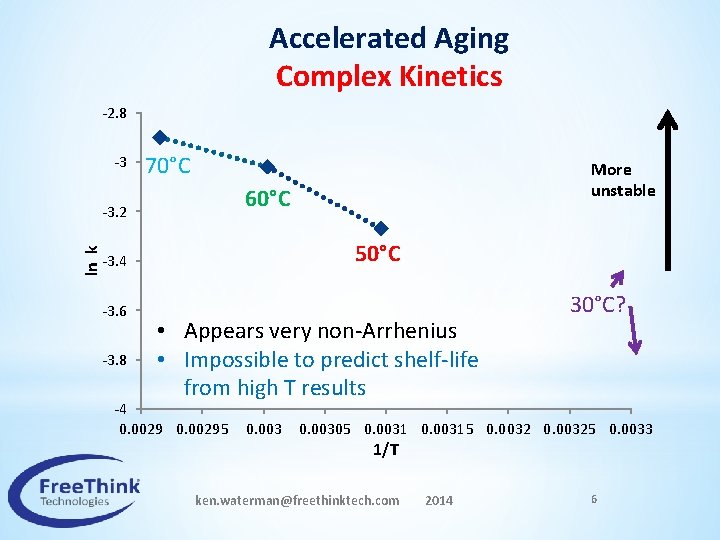
Accelerated Aging Complex Kinetics -2. 8 -3 70°C 60°C ln k -3. 2 50°C -3. 4 -3. 6 -3. 8 More unstable • Appears very non-Arrhenius • Impossible to predict shelf-life from high T results -4 0. 00295 0. 003 30°C? 0. 00305 0. 00315 0. 00325 0. 0033 1/T ken. waterman@freethinktech. com 2014 6

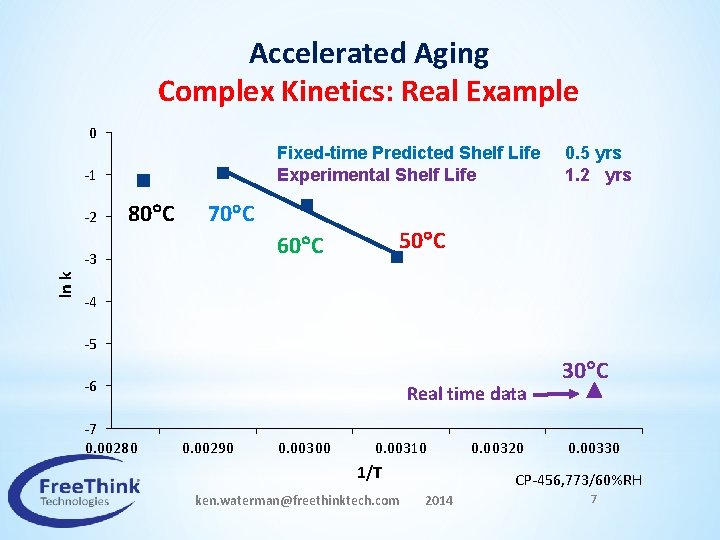
Accelerated Aging Complex Kinetics: Real Example 0 Fixed-time Predicted Shelf Life Experimental Shelf Life -1 -2 80 C 70 C ln k 50 C 60 C -3 0. 5 yrs 1. 2 yrs -4 -5 -6 -7 0. 00280 Real time data 0. 00290 0. 00300 0. 00310 1/T ken. waterman@freethinktech. com 2014 0. 00320 30 C 0. 00330 CP-456, 773/60%RH 7

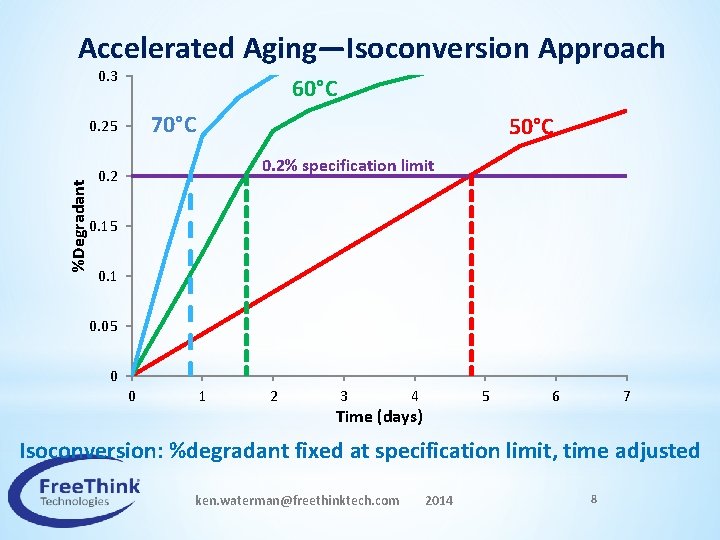
Accelerated Aging—Isoconversion Approach 0. 3 60°C 70°C %Degradant 0. 25 50°C 0. 2% specification limit 0. 2 0. 15 0. 1 0. 05 0 0 1 2 3 4 Time (days) 5 6 7 Isoconversion: %degradant fixed at specification limit, time adjusted ken. waterman@freethinktech. com 2014 8

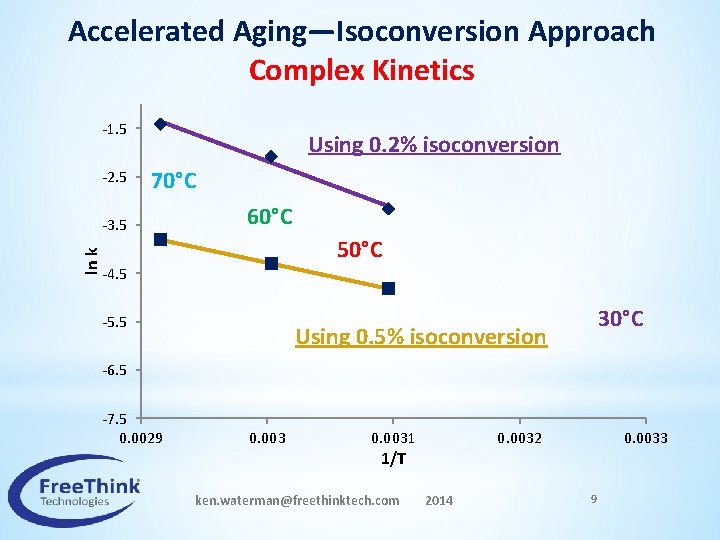
Accelerated Aging—Isoconversion Approach Complex Kinetics -1. 5 -2. 5 Using 0. 2% isoconversion 70°C ln k -3. 5 60°C 50°C -4. 5 -5. 5 30°C Using 0. 5% isoconversion -6. 5 -7. 5 0. 0029 0. 0031 1/T ken. waterman@freethinktech. com 2014 0. 0032 0. 0033 9

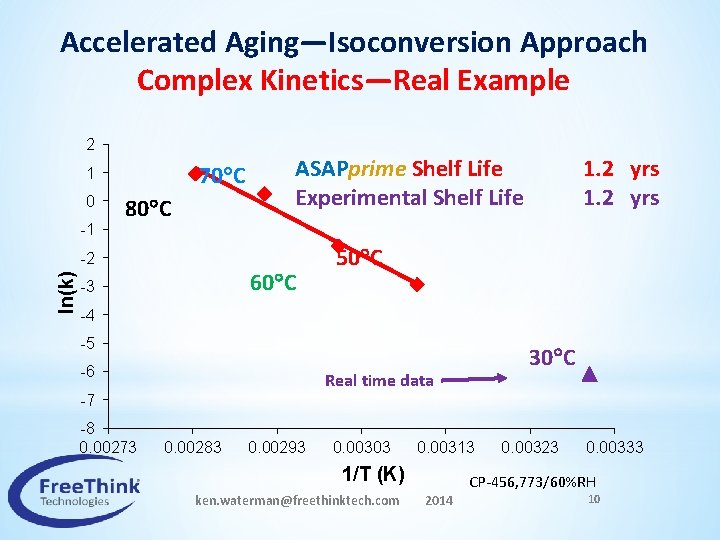
Accelerated Aging—Isoconversion Approach Complex Kinetics—Real Example 2 70 C 1 0 -1 80 C ASAPprime Shelf Life Experimental Shelf Life ln(k) -2 60 C -3 1. 2 yrs 50 C -4 -5 -6 30 C Real time data -7 -8 0. 00273 0. 00283 0. 00293 0. 00303 0. 00313 1/T (K) ken. waterman@freethinktech. com 2014 0. 00323 0. 00333 CP-456, 773/60%RH 10

More Detailed Example A k 1 B k 2 C • Time points @ 0, 3, 7, 14 and 28 days • Shelf-life @25°C using 50, 60 and 70°C • k 1 = 0. 000113%/d k 2 = 0. 01125%/d @50°C for “B” example (25 kcal/mol) • k 1 = 0. 000112%/d k 2 = 0. 09%/d @50°C for “C” example (25 kcal/mol) ken. waterman@freethinktech. com 2014 11

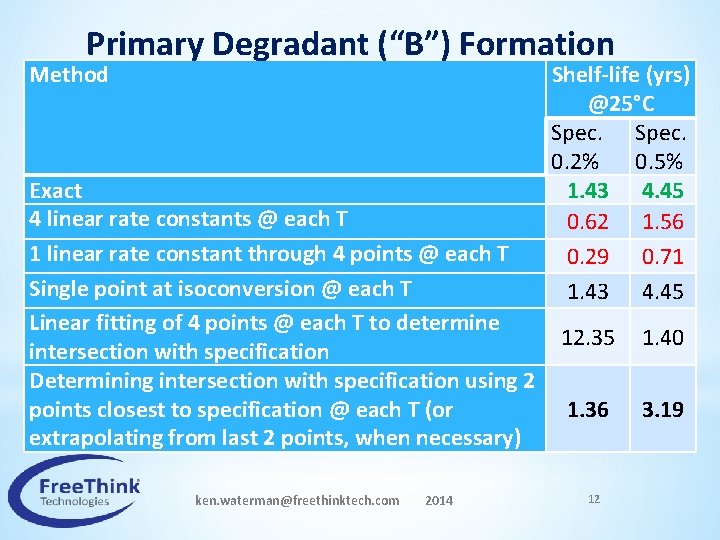
Primary Degradant (“B”) Formation Method Shelf-life (yrs) @25°C Spec. 0. 2% 0. 5% 1. 43 4. 45 0. 62 1. 56 0. 29 0. 71 1. 43 4. 45 Exact 4 linear rate constants @ each T 1 linear rate constant through 4 points @ each T Single point at isoconversion @ each T Linear fitting of 4 points @ each T to determine 12. 35 intersection with specification Determining intersection with specification using 2 1. 36 points closest to specification @ each T (or extrapolating from last 2 points, when necessary) ken. waterman@freethinktech. com 2014 12 1. 40 3. 19

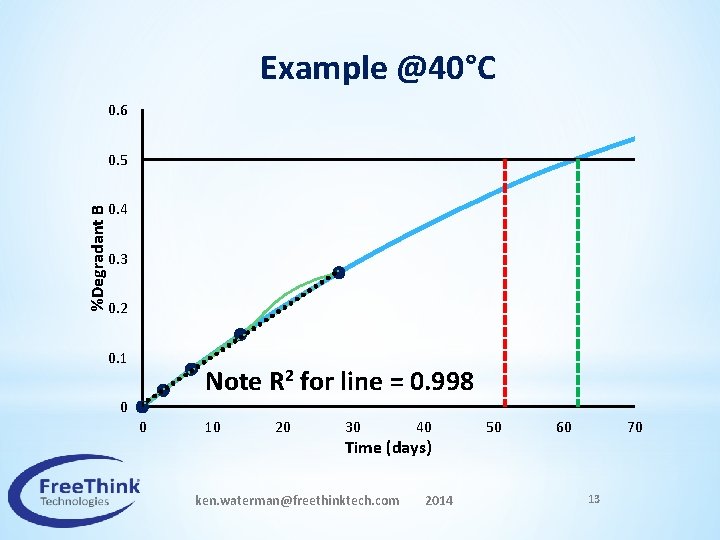
Example @40°C 0. 6 %Degradant B 0. 5 0. 4 0. 3 0. 2 0. 1 Note R 2 for line = 0. 998 0 0 10 20 30 40 Time (days) ken. waterman@freethinktech. com 2014 50 60 70 13

Secondary Degradant (“C”) Formation Method Shelf-life (yrs) @25°C Spec. 0. 2% 0. 5% 2. 02 4. 01 16. 64 41. 61 3. 29 8. 21 2. 02 4. 01 Exact 4 linear rate constants @ each T 1 linear rate constant through 4 points @ each T Single point at isoconversion @ each T Linear fitting of 4 points @ each T to determine 2. 75 intersection with specification Determining intersection with specification using 2 points closest to specification @ each T (or 2. 06 extrapolating from last 2 points, when necessary) ken. waterman@freethinktech. com 2014 14 7. 56 4. 78

Accuracy • Both isoconversion and rate constant methods accurate when behavior is simple • Only isoconversion is accurate when degradant formation is complex • Carrying out degradation to bracket specification limit at each condition will increase reliability of modeling ken. waterman@freethinktech. com 2014 15

Estimating Uncertainty • Need to use isoconversion for accuracy: defines a 2 step process • Estimating uncertainty in isoconversion from degradant vs. time data • Propagating to ambient using Arrhenius equation • Error bars for degradant formation are not uniform • Constant relative standard deviation (RSD) • Minimum error of limit of detection (LOD) ken. waterman@freethinktech. com 2014 16

Isoconversion Uncertainty Methods ken. waterman@freethinktech. com 2014 17

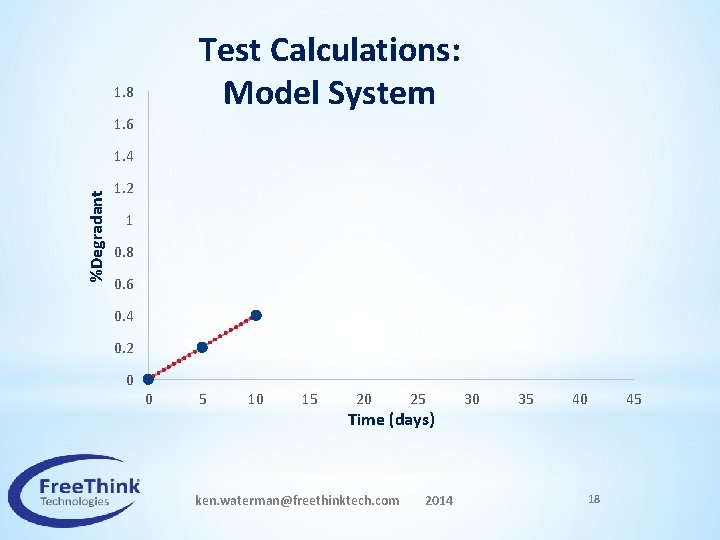
Test Calculations: Model System 1. 8 1. 6 %Degradant 1. 4 1. 2 1 0. 8 0. 6 0. 4 0. 2 0 0 5 10 15 20 25 Time (days) ken. waterman@freethinktech. com 2014 30 35 40 18 45

Calculations Where Formulae Exist Calculation Method Regression Interval 5 Days (Interpolation) 0. 023% 40 -Days (Extrapolation) 0. 102% Confidence Interval 0. 012% 0. 100% Stochastic 0. 012% 0. 099% Non-Stochastic 0. 012% 0. 100% Extrema 0. 020% 0. 147% Fixed SD = 0. 02% ken. waterman@freethinktech. com 2014 19

Isoconversion Uncertainty • CI too narrow in interpolation regions (< experimental σ); also does not take into account error of fit • RI better represents error for predictions • RI and CI converge with extrapolation • Extrema mimics RI in interpolation; more conservative in extrapolation • Note: scientifically less confident in isoconversion extrapolations (model fit) ken. waterman@freethinktech. com 2014 20

Calculations Where Formulae Do Not Exist Calculation Method Stochastic Non-Stochastic Extrema 5 Days (Interpolation) 0. 016% 40 -Days (Extrapolation) 0. 166% 0. 027% 0. 223% Fixed RSD = 10% with minimum error of 0. 02% (LOD) ken. waterman@freethinktech. com 2014 21

Arrhenius Fitting Uncertainty • Can use full isoconversion distribution from Monte. Carlo calculation • Can use extrema calculation • Normalized about time (x-axis, degradant set by specification limit) • Normalized about degradant (y-axis, time set by zero-error intercept with specification limit) ken. waterman@freethinktech. com 2014 22

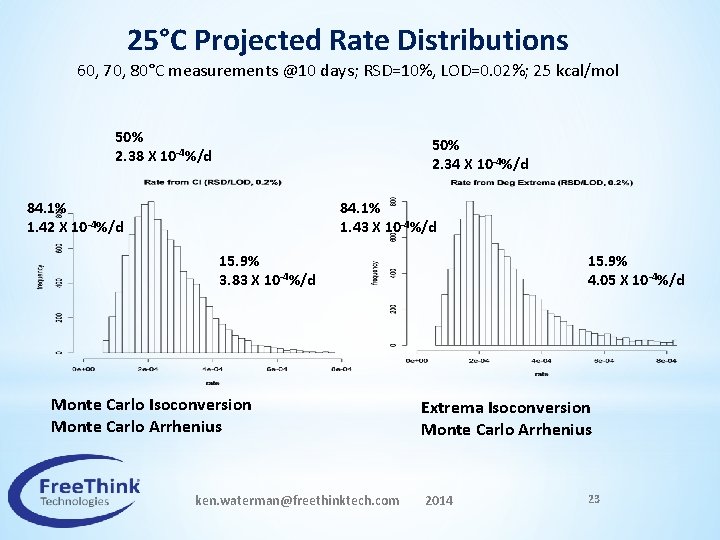
25°C Projected Rate Distributions 60, 70, 80°C measurements @10 days; RSD=10%, LOD=0. 02%; 25 kcal/mol 50% 2. 38 X 10 -4%/d 50% 2. 34 X 10 -4%/d 84. 1% 1. 42 X 10 -4%/d 84. 1% 1. 43 X 10 -4%/d 15. 9% 4. 05 X 10 -4%/d 15. 9% 3. 83 X 10 -4%/d Monte Carlo Isoconversion Monte Carlo Arrhenius Extrema Isoconversion Monte Carlo Arrhenius ken. waterman@freethinktech. com 2014 23

Arrhenius Fitting Uncertainty • Distribution of ambient rates from Monte-Carlo or extrema calculations very similar • In both cases, rate is not normally distributed • Probabilities need to use a cumulative distribution function ken. waterman@freethinktech. com 2014 24

Arrhenius Fitting Uncertainty • Can be solved in logarithmic (linear) or exponential (non-linear) form • With perfect data, point estimates of rate (shelf-life) will be identical • A distribution at each point will generate imperfect fits • Least squares will minimize difference between actual and calculated points • Non-linear will weight high T more heavily • Constant RSD means that higher rates will have greater errors ken. waterman@freethinktech. com 2014 25

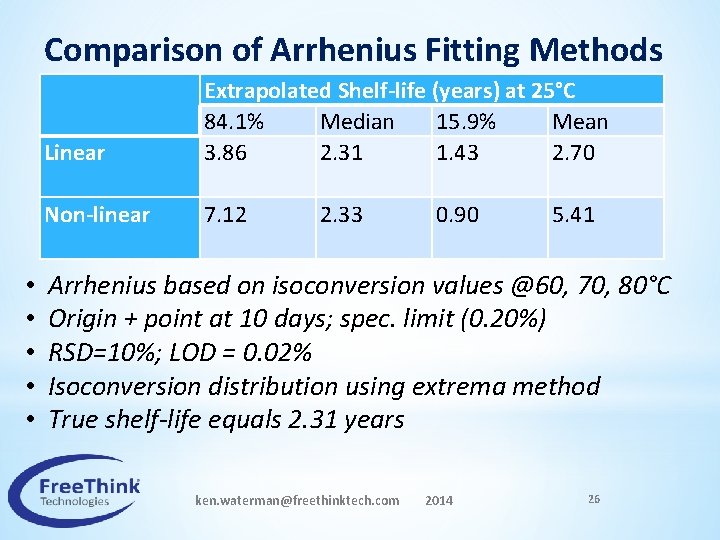
Comparison of Arrhenius Fitting Methods Linear Non-linear • • • Extrapolated Shelf-life (years) at 25°C 84. 1% Median 15. 9% Mean 3. 86 2. 31 1. 43 2. 70 7. 12 2. 33 0. 90 5. 41 Arrhenius based on isoconversion values @60, 70, 80°C Origin + point at 10 days; spec. limit (0. 20%) RSD=10%; LOD = 0. 02% Isoconversion distribution using extrema method True shelf-life equals 2. 31 years ken. waterman@freethinktech. com 2014 26

Arrhenius Fitting Uncertainty • Non-linear least squares fitting gives larger, less normal distributions of ambient rates • Non-linear fitting’s greater weighting of higher temperatures makes non-Arrhenius behavior more likely to cause inaccuracies • Since linear is also less computationally challenging, recommend use of linear fitting ken. waterman@freethinktech. com 2014 27

Low Degradant vs. Standard Deviation • For low degradation rate (with respect to the SD), isoconversion less symmetric • Becomes discontinuous @Δdeg = 0 (isoconversion = ∞) for any sampled point • Can resolve by clipping points with MC • Distribution meaning when most points removed? • Can use extrema • Define behavior with no regression line isoconversion • Can define mean from first extrema intercept (2 X value) • No perfect answers—modeling better when data show change ken. waterman@freethinktech. com 2014 28

Notes • ICH guidelines allow ± 2 C and ± 5%RH— average drug product shows a factor of 2. 7 shelf-life difference within this range • ASAP modeling uses both T and RH, both potentially changing with time—errors will change accordingly • Assume mathematics the same, but need to focus on instantaneous rates ken. waterman@freethinktech. com 2014 29

Conclusions • Modeling drug product shelf-life from accelerated data more accurate using isoconversion • Isoconversion more accurate using points bracketing specification limit than using all points • With isoconversion, regression interval (not confidence interval) includes error of fit, but difficult to calculate with varying SD • Extrema method reasonably approximates RI for interpolation; more conservative for extrapolation • Linear fitting of Arrhenius equation preferred ken. waterman@freethinktech. com 2014 30

Notes on King, Kung, Fung “Statistical prediction of drug stability based on non-linear parameter estimation” J. Pharm. Sci. 1984; 73: 657 -662 • Used rates based on each time point independently • Changing rate constants not projected accurately for shelf-life • Gives greater precision by treating each point as equivalent, even when far from isoconversion (32 points at 4 T’s gives better error bars than just 4 isoconversion values: more precise, but more likely to be wrong) • Non-linear fitting to Arrhenius • Weights higher T more heavily (and where they had most degradation) • Made more sense with constant errors used for loss of potency • Non-linear fitting in general bigger, less symmetric error bars, more likely to be in error if mechanism shift with T • Used mean and SD for linear fitting, even when not normally distributed (i. e. , not statistically valid method) • Do not recommend general use of KKF method (fine for ideal behavior, loss of potency) ken. waterman@freethinktech. com 2014 31