A sample problem 3 43 Allicin is the

A sample problem 3. 43) Allicin is the compound responsible for the characteristic smell of garlic. An analysis of the compound gives the following percent composition by mass: C: 44. 4%, H: 6. 21%, S: 39. 5%, O: 9. 86%. Calculate its empirical formula. What is its molecular formula given that its molar mass is about 162 g? empirical formula = molecular formula = C 6 H 10 S 2 O *Note that we arbitrarily chose a 100 -g sample to make our math easier. 3/10/2021 1

Another sample problem 3. 52) The empirical formula of a compound is CH. If the molar mass of this compound is about 78 g, what is its molecular formula? 1. 2. 3. Figure out molar mass of the empirical formula. Divide the molar mass of the compound by the molar mass of the empirical formula. Multiply each subscript on the empirical formula by this quotient to get the molecular formula. 78/13. 01=6 3/10/2021 C 6 H 6 2

Yet another sample problem Practice exercise, p. 71) A sample of a compound containing boron and hydrogen contains 6. 444 g of boron and 1. 803 g of hydrogen. The molar mass of the compound is about 30 g. What is its molecular formula? 1. 2. 3. Figure out molar mass of the empirical formula. Divide the molar mass of the compound by the molar mass of the empirical formula. Multiply each subscript in the empirical formula by this whole number to get the molecular formula. B 2 H 6 3/10/2021 3

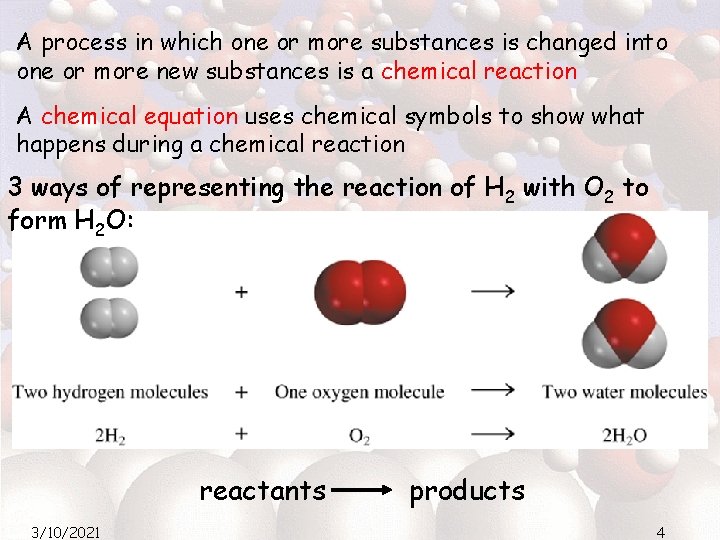
A process in which one or more substances is changed into one or more new substances is a chemical reaction A chemical equation uses chemical symbols to show what happens during a chemical reaction 3 ways of representing the reaction of H 2 with O 2 to form H 2 O: reactants 3/10/2021 products 4

How to “Read” Chemical Equations 2 Mg + O 2 2 Mg. O 2 atoms Mg + 1 molecule O 2 makes 2 formula units Mg. O 2 moles Mg + 1 mole O 2 makes 2 moles Mg. O 48. 6 grams Mg + 32. 0 grams O 2 makes 80. 6 g Mg. O 2 grams Mg + 1 gram O 2 makes 2 g Mg. O *Note: Stoichiometric coefficients = atoms or moles… NOT grams! 3/10/2021 5

Balancing Chemical Equations 1. Write the correct formula(s) for the reactants on the left side and the correct formula(s) for the product(s) on the right side of the equation. Ethane (C 2 H 6) reacts with oxygen to form carbon dioxide & water C 2 H 6 + O 2 CO 2 + H 2 O 2. Change the numbers in front of the formulas (coefficients) to make the number of atoms of each element the same on both sides of the equation. Do not change the subscripts. 2 C 2 H 6 3/10/2021 NOT C 4 H 12 6

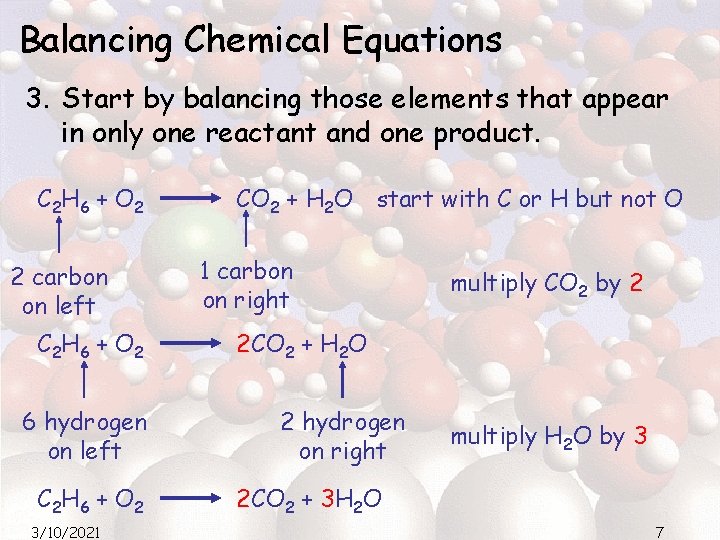
Balancing Chemical Equations 3. Start by balancing those elements that appear in only one reactant and one product. C 2 H 6 + O 2 2 carbon on left C 2 H 6 + O 2 6 hydrogen on left C 2 H 6 + O 2 3/10/2021 CO 2 + H 2 O start with C or H but not O 1 carbon on right multiply CO 2 by 2 2 CO 2 + H 2 O 2 hydrogen on right multiply H 2 O by 3 2 CO 2 + 3 H 2 O 7

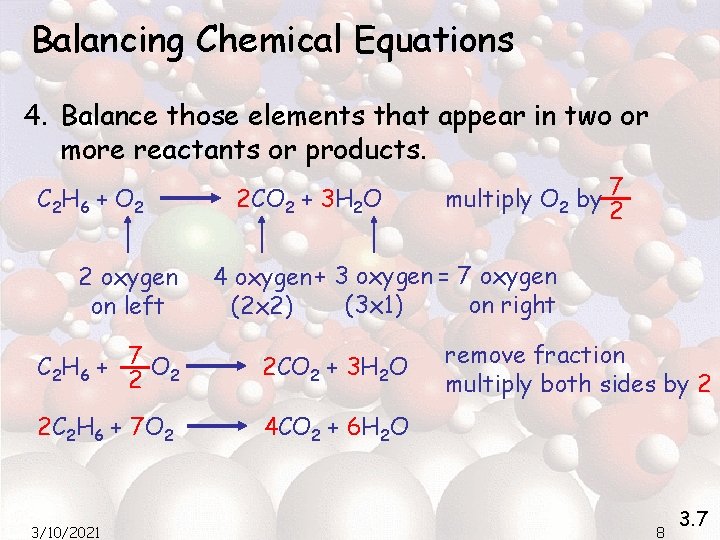
Balancing Chemical Equations 4. Balance those elements that appear in two or more reactants or products. C 2 H 6 + O 2 2 oxygen on left 2 CO 2 + 3 H 2 O 4 oxygen + 3 oxygen = 7 oxygen (3 x 1) on right (2 x 2) C 2 H 6 + 7 O 2 2 2 CO 2 + 3 H 2 O 2 C 2 H 6 + 7 O 2 4 CO 2 + 6 H 2 O 3/10/2021 multiply O 2 by 7 2 remove fraction multiply both sides by 2 8 3. 7

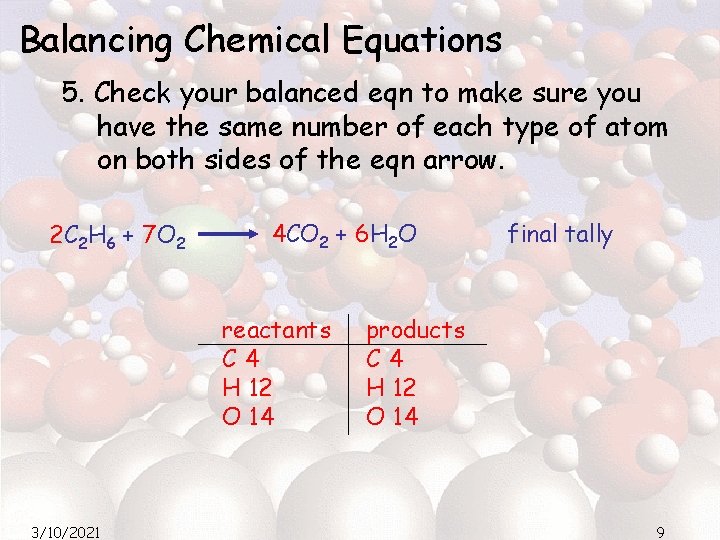
Balancing Chemical Equations 5. Check your balanced eqn to make sure you have the same number of each type of atom on both sides of the eqn arrow. 2 C 2 H 6 + 7 O 2 4 CO 2 + 6 H 2 O reactants C 4 H 12 O 14 3/10/2021 final tally products C 4 H 12 O 14 9

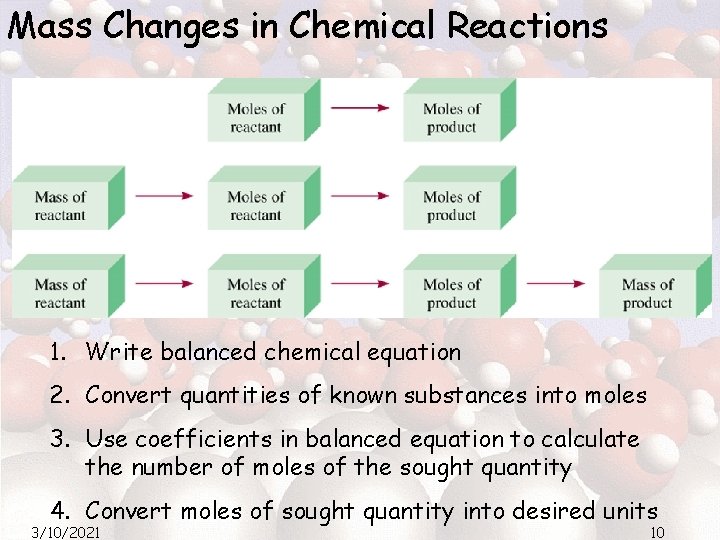
Mass Changes in Chemical Reactions 1. Write balanced chemical equation 2. Convert quantities of known substances into moles 3. Use coefficients in balanced equation to calculate the number of moles of the sought quantity 4. Convert moles of sought quantity into desired units 3/10/2021 10

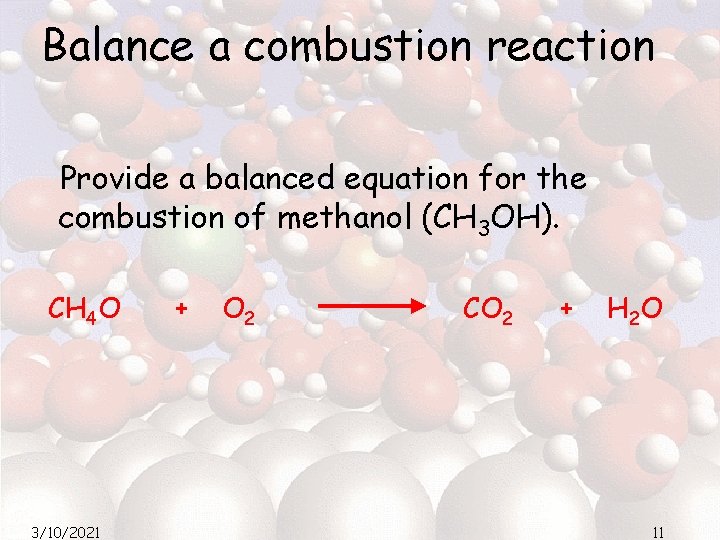
Balance a combustion reaction Provide a balanced equation for the combustion of methanol (CH 3 OH). CH 4 O 3/10/2021 + O 2 CO 2 + H 2 O 11

Balance a combustion reaction Provide a balanced equation for the combustion of methanol (CH 3 OH). 2 CH 4 O 3/10/2021 + 3 O 2 2 CO 2 + 4 H 2 O 12

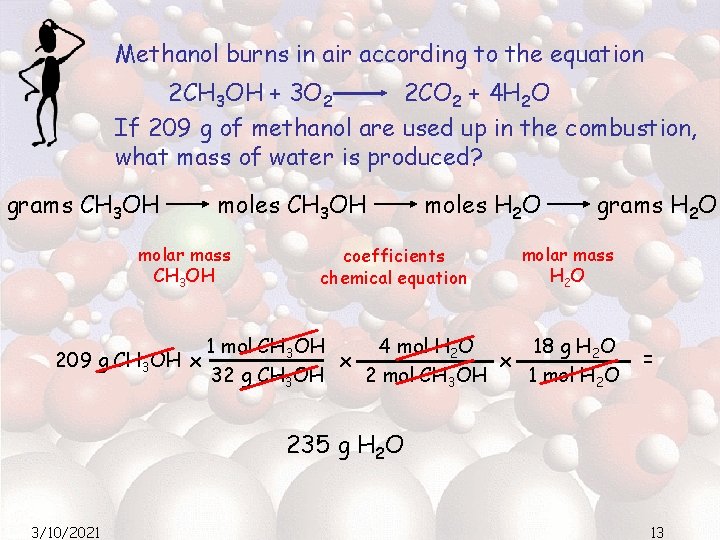
Methanol burns in air according to the equation 2 CH 3 OH + 3 O 2 2 CO 2 + 4 H 2 O If 209 g of methanol are used up in the combustion, what mass of water is produced? grams CH 3 OH moles CH 3 OH molar mass CH 3 OH 209 g CH 3 OH x moles H 2 O coefficients chemical equation grams H 2 O molar mass H 2 O 4 mol H 2 O 18 g H 2 O 1 mol CH 3 OH x x 32 g CH 3 OH 2 mol CH 3 OH 1 mol H 2 O = 235 g H 2 O 3/10/2021 13

Limiting Reagents When a chemist carries out a reaction, the reactants are usually not present in stoichiometric amounts, that is, in the proportions indicated by the balanced equation. It is common to use the cheaper reactant in excess to ensure that all of the expensive reagent is consumed. The more expensive reagent is the limiting reagent and is often completely consumed in a reaction. 3/10/2021 14

Do You Understand Limiting Reagents? In one process, 124 g of Al are reacted with 601 g of Fe 2 O 3. Which reactant is the limiting reagent? 2 Al + Fe 2 O 3 g Al mol Al g Fe 2 O 3 124 g Al x mol Fe 2 O 3 needed OR mol Al needed mol Fe 2 O 3 1 mol Al 27 g Al Al 2 O 3 + 2 Fe x 1 mol Fe 2 O 3 2 mol Al Start with 124 g Al g Fe 2 O 3 needed g Al needed 160 g Fe 2 O 3 = 367 g Fe 2 O 3 x 1 mol Fe 2 O 3 need 367 g Fe 2 O 3 Have more Fe 2 O 3 (601 g) so Al is limiting reagent 3/10/2021 15